2022--2023学年中考数学专题训练——相似三角形的判定和性质(Word版,含解析)
文档属性
| 名称 | 2022--2023学年中考数学专题训练——相似三角形的判定和性质(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 17:46:45 | ||
图片预览




文档简介
中考专题训练——相似三角形的判定和性质
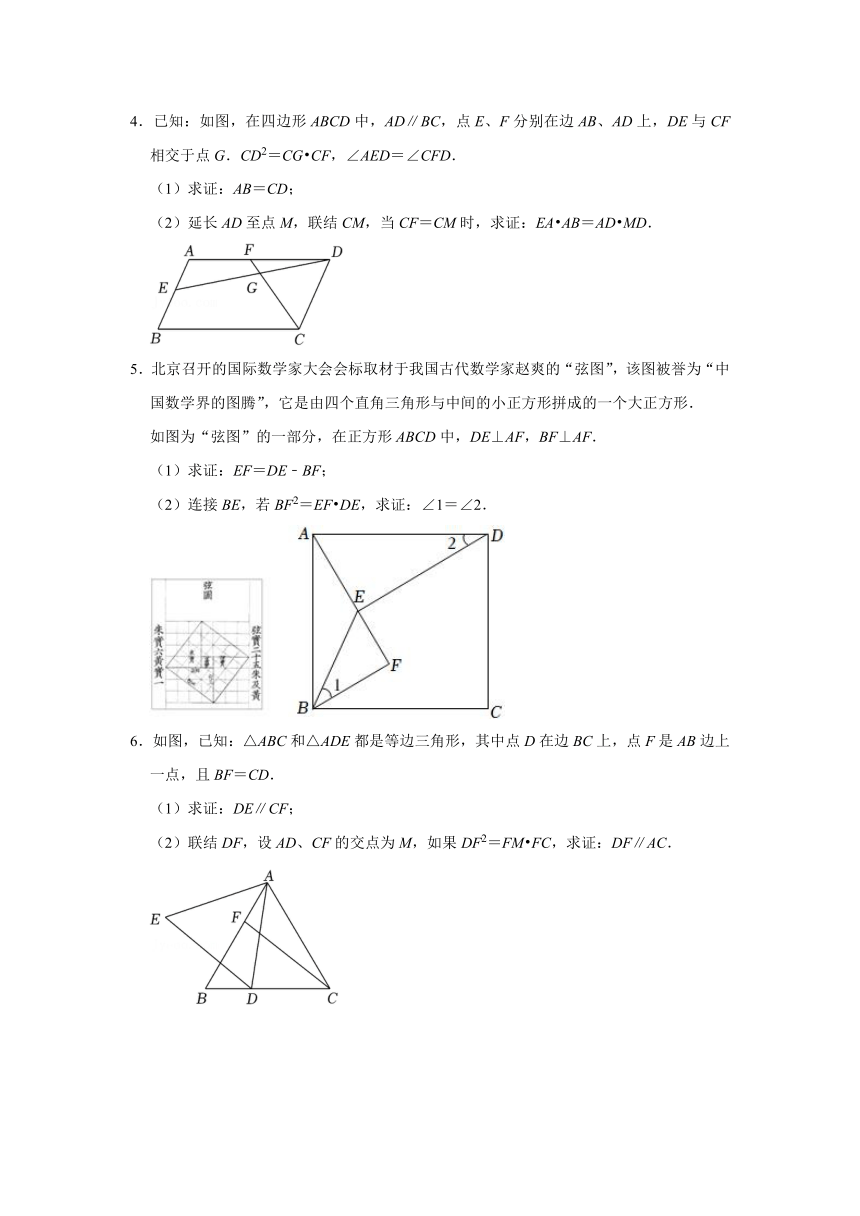
1.如图,E是菱形ABCD对角线AC上一点,四边形BGFE是矩形.点F,G分别在DC,BC上.
(1)求证:∠CFG=∠ABE.
(2)若BE=4,,求FM的长.
2.如图,在 ABCD中,AE⊥BC于点E,点F在BC的延长线上,且CF=BE,连接AC,DF.
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,AE=4,CF=2,求.
3.如图,已知正方形ABCD的边长为a,正方形CEFG的边长为b(b<a),点E在CD边上,点G在BC延长线上,点H为BC上的点,连接DF,DH.
(1)当DH⊥DF时,求证:△DEF∽△HCD.
(2)若点H为BC的中点,在(1)的条件下,求出a与b满足的关系式.
4.已知:如图,在四边形ABCD中,AD∥BC,点E、F分别在边AB、AD上,DE与CF相交于点G.CD2=CG CF,∠AED=∠CFD.
(1)求证:AB=CD;
(2)延长AD至点M,联结CM,当CF=CM时,求证:EA AB=AD MD.
5.北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“弦图”,该图被誉为“中国数学界的图腾”,它是由四个直角三角形与中间的小正方形拼成的一个大正方形.
如图为“弦图”的一部分,在正方形ABCD中,DE⊥AF,BF⊥AF.
(1)求证:EF=DE﹣BF;
(2)连接BE,若BF2=EF DE,求证:∠1=∠2.
6.如图,已知:△ABC和△ADE都是等边三角形,其中点D在边BC上,点F是AB边上一点,且BF=CD.
(1)求证:DE∥CF;
(2)联结DF,设AD、CF的交点为M,如果DF2=FM FC,求证:DF∥AC.
7.如图,△ABC中,AB=AC.
(1)尺规作图:作AB的垂直平分线DE,分别交AB、AC于点E和点D.(保留作图痕迹,不写作法);
(2)连接BD,若BD=BC=2,求AC的长.
(3)在(2)的条件下,cosC= .
8.如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边与AB交于点E.
(1)求证:Rt△AEP∽Rt△DPC;
(2)当∠CPD=30°时,求AE的长.
9.如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
10.已知:如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,点F在边AD上,CF交BD于点G,CF∥AE,CF=BD.
(1)求证:四边形AECF为菱形;
(2)如果∠DCG=∠DEC,求证:AE2=AD DC.
11.如图,在矩形ABCD中,AB=3,BC=5,BE平分∠ABC交AD于点E.连接CE,点F是BE上一动点,过点F作FG∥CE交BC于点G.将△BFG绕点B旋转得到△BF'G'.
(1)连接CG',EF',求证:△BEF'∽△BCG';
(2)当点G'恰好落在直线AE上时,若BF=3,求EG'的值.
12.如图,正方形ABCD,E、F分别是边AB,BC的中点,AF与DE,DB分别交于点M,N.
(1)求证:AF=DE,AF⊥DE.
(2)求AM:MN:NF的值.
13.问题背景
如图1,在△ABC中,点D,E分别在AC,AB上,2∠EDB+∠BDC=180°,∠DEB=90°,求证:AE=BE.
变式迁移
如图2,在四边形DEBC中,2∠EDB+∠BDC=180°,∠DEB=90°,DF∥EB,DF分别交CE,BC于点G,F,求证:DG=FG.
拓展应用
如图3,在四边形DECB中,2∠DBE+∠EBC=180°,∠EDB=∠DCB,,且n>1,直接写出的值.
14.问题提出
(1)如图①正三角形ABC,边长为4,D、E是边AB、AC的中点,P在BC边上,则△PDE的面积为 ;
问题解决
(2)如图②,某小区有一块五边形空地ABCDE,CD⊥DE,AE∥CD,CB=CD=40m,AE=10米,∠ABC=∠BCD=120°,物业想在这块空地中划出一块△MNP区域来种植草皮,其他区域种植花卉.已知种植花卉每平方米200元,种植草皮每平方米100元.要求M,N,P分别位于AB,ED,CD边上,且MN∥CD,要使种植费用的造价最低,种植草皮的△MNP的面积应该满足什么条件?并求出费用的最小值.
15.如图,在正方形ABCD中,点E在BC边上,连接AE,在BC延长线上作EF=AE,连接AF交CD于点G,设CE:EB=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若G点为CD的中点,①求证:EG⊥AF.②求λ的值.
16.如图,已知△ABC,点D,E分别在BC,CA上,且满足AD=AB,EB=EC.
(1)用直尺和圆规确定点D,E;(保留作图痕迹,不写作法)
(2)连接AD,EB,AD与EB交于点F.
①求证:△BDF∽△CBA;
②若∠BAC=90°,AB=3,AC=4,则DF的长为 .
17.如图,△ABC是等腰直角三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,DE⊥DF,∠DEF=45°,DF的延长线与BC的延长线相交于点G.
(1)求证:△BDE∽△CEF;
(2)若AD=1,AF=2,求EC的长;
(3)若,求的值.
18.如图,在正方形ABCD中,点E是边AD上的一点(不与A、D重合),点F在边DC延长线上,CF=AE,连接BE、BF、EF,EF交BC于点M,交对角线BD于N.
(1)求证:∠BEF=45°;
(2)若BE平分∠ABD,求证:BE2=AB BM;
(3)若DE:EA=3:2,则EN:NM:MF= (直接写答案).
19.如图1,在四边形ABCD中,∠ABC=∠BCD,过点A作AE∥DC交BC边于点E,过点E作EF∥AB交CD边于点F,连接AF,过点C作CH∥AF交AE于点H,连接BH.
(1)求证:△ABH≌△EAF;
(2)如图2,若BH的延长线经过AF的中点M,求的值.
20.如图1,在矩形ABCD中,AB=5,AD=8,点E在边CD上,tan∠BAE=2,点F是线改AE上一点,连接CF.
(1)连接BF,请用尺规作图法作FG⊥AB,垂足为G点(保留作图痕迹,不要求写出作法).若tan∠ABF=,求线段AF的长.
(2)如图2,若CF=BC,AE的延长线与BC的延长线交于点H,求△CEF的面积.
参考答案与试题解析
1.如图,E是菱形ABCD对角线AC上一点,四边形BGFE是矩形.点F,G分别在DC,BC上.
(1)求证:∠CFG=∠ABE.
(2)若BE=4,,求FM的长.
【分析】(1)根据菱形的性质可得AB∥CD,从而可得∠CAB=∠DCA,根据矩形的性质可得BE∥FG,从而可得∠BEM=∠FME,然后利用三角形的外角可得∠BEM=∠BAE+∠ABE,∠FME=∠ACD+∠CFG,即可解答;
(2)根据矩形的性质可得EB=FG=4,∠EFG=∠FGB=90°,EF∥BG,再利用(1)的结论在Rt△FGC中,利用锐角三角函数的定义和勾股定理求出CG,CF的长,根据菱形的性质可得AD∥BC,AD=DC,从而可得AD∥EF,∠DAC=∠DCA,进而可得∠FEC=∠DCA,然后利用等角对等边可得FE=FC=5,最后证明8字模型相似三角形△EFM∽△CGM,利用相似三角形的性质进行计算即可解答.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠CAB=∠DCA,
∵四边形BGFE是矩形,
∴BE∥FG,
∴∠BEM=∠FME,
∵∠BEM=∠BAE+∠ABE,∠FME=∠ACD+∠CFG,
∴∠CFG=∠ABE;
(2)解:∵四边形BGFE是矩形,
∴EB=FG=4,∠EFG=∠FGB=90°,EF∥BG,
∴∠FGC=180°﹣∠FGB=90°,
∵,∠CFG=∠ABE,
∴tan∠CFG=,
∴CG=FG tan∠CFG=4×=3,
∴FC===5,
∵四边形ABCD是菱形,
∴AD∥BC,AD=DC,
∴AD∥EF,
∴∠DAC=∠FEC,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠FEC=∠DCA,
∴FE=FC=5,
∵∠EFG=∠FGC=90°,∠EMF=∠CMG,
∴△EFM∽△CGM,
∴=,
∴=,
∴FM=,
∴FM的长为.
2.如图,在 ABCD中,AE⊥BC于点E,点F在BC的延长线上,且CF=BE,连接AC,DF.
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,AE=4,CF=2,求.
【分析】(1)先证明四边形AEFD是平行四边形,再证明∠AEF=90°即可;
(2)根据矩形的性质和相似三角形的判定和性质解答即可.
【解答】(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,
∴∠AEC=∠DFC=90°,AE=DF=4,
∴∠EAC+∠ECA=90°,
∵∠ACD=90°,
∴∠ECA+∠DCF=90°,
∴∠EAC=∠DCF,
∴△AEC∽△CFD,
∴==,
∴EC=2AE=8,
解法一:∴===4.
解法二:∴=()2=()2=4.
3.如图,已知正方形ABCD的边长为a,正方形CEFG的边长为b(b<a),点E在CD边上,点G在BC延长线上,点H为BC上的点,连接DF,DH.
(1)当DH⊥DF时,求证:△DEF∽△HCD.
(2)若点H为BC的中点,在(1)的条件下,求出a与b满足的关系式.
【分析】(1)证明∠EDF=∠DHC,再结合90°角可以证明△DEF∽△HCD;
(2)根据(1)中的相似得到对应边成比例,可以得到关于a和b的等式即可得解.
【解答】(1)证明:∵四边形ABCD,CEFG都是正方形,
∴∠HCD=90°,∠CEF=∠DEF=90°,
∴∠DEF=∠HCD=90°,
∴∠HDC+∠DHC=90°,
又∵DH⊥DF,
∴∠HDF=90°,
∴∠HDC+∠EDF=90°,
∴∠EDF=∠DHC,
∴△DEF∽△HCD.
(2)解:∵点H为BC的中点,
∴HC=,
∵CD=a,CE=EF=b,∴DE=a﹣b,
由(1)可知△DEF∽△HCD,
∴,
∴,
∴,
即a与b满足的关系式为a=.
4.已知:如图,在四边形ABCD中,AD∥BC,点E、F分别在边AB、AD上,DE与CF相交于点G.CD2=CG CF,∠AED=∠CFD.
(1)求证:AB=CD;
(2)延长AD至点M,联结CM,当CF=CM时,求证:EA AB=AD MD.
【分析】(1)根据已知可得=,从而可得△CDG∽△CFD,然后利用相似三角形的性质可得∠CDG=∠CFD,从而可得∠CDG=∠AED,进而可得AB∥CD,最后证明四边形ABCD是平行四边形,从而利用平行四边形的性质即可解答;
(2)根据等腰三角形的性质可得∠CFD=∠M,从而可得∠AED=∠M,然后利用平行线的性质可得∠A=∠CDM,从而可证△AED∽△DMC,进而利用相似三角形的性质即可解答.
【解答】证明:(1)∵CD2=CG CF,
∴=,
∵∠DCG=∠DCF,
∴△CDG∽△CFD,
∴∠CDG=∠CFD,
∵∠AED=∠CFD,
∴∠CDG=∠AED,
∴AB∥CD,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD;
(2)如图:
∵CF=CM,
∴∠CFD=∠M,
∵∠AED=∠CFD,
∴∠AED=∠M,
∵AB∥CD,
∴∠A=∠CDM,
∴△AED∽△DMC,
∴=,
∴AE DC=AD DM,
∵AB=DC,
∴EA AB=AD MD.
5.北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“弦图”,该图被誉为“中国数学界的图腾”,它是由四个直角三角形与中间的小正方形拼成的一个大正方形.
如图为“弦图”的一部分,在正方形ABCD中,DE⊥AF,BF⊥AF.
(1)求证:EF=DE﹣BF;
(2)连接BE,若BF2=EF DE,求证:∠1=∠2.
【分析】(1)利用正方形的性质可得AB=AD,∠BAD=90°,从而可得∠BAF+∠DAE=90°,根据垂直定义可得∠AED=∠F=90°,从而可得∠BAF+∠ABF=90°,然后利用同角的余角相等可得∠DAE=∠ABF,从而可证△ABF≌△DAE,D进而可得DE=AF,AE=BF,即可解答;
(2)利用(1)的结论可得DE=AF,∠BAF=∠ADE=∠2,从而可得=,进而可得△FBE∽△FAB,然后利用相似三角形的性质可得∠1=∠BAF,即可解答.
【解答】证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAF+∠DAE=90°,
∵DE⊥AF,BF⊥AF,
∴∠AED=∠F=90°,
∴∠BAF+∠ABF=90°,
∴∠DAE=∠ABF,
∴△ABF≌△DAE(AAS),
∴DE=AF,AE=BF,
∵EF=AF﹣AE,
∴EF=DE﹣BF;
(2)∵△ABF≌△DAE,
∴DE=AF,∠BAF=∠ADE=∠2,
∵BF2=EF DE,
∴=,
∴=,
∵∠F=∠F,
∴△FBE∽△FAB,
∴∠1=∠BAF,
∴∠1=∠2.
6.如图,已知:△ABC和△ADE都是等边三角形,其中点D在边BC上,点F是AB边上一点,且BF=CD.
(1)求证:DE∥CF;
(2)联结DF,设AD、CF的交点为M,如果DF2=FM FC,求证:DF∥AC.
【分析】(1)由等边三角形的性质证明△ACD≌△CBF,得出∠CAD=∠BCF,由等边三角形的性质及三角形外角的性质得出∠BDE=∠CAD,进而得出∠BDE=∠BCF,即可证明DE∥CF;
(2)先证明△DFM∽△CFD,得出∠FDM=∠FCD,由∠CAD=∠BCF,得出∠FDM=∠CAD,即可证明DF∥AC.
【解答】证明:(1)如图1,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
在△ACD和△CBF中,
,
∴△ACD≌△CBF(SAS),
∴∠CAD=∠BCF,
∵△ADE是等边三角形,
∴∠ADE=∠ACB=60°,
∵∠ADE+∠BDE=∠ACB+∠CAD,
∴∠BDE=∠CAD,
∴∠BDE=∠BCF,
∴DE∥CF;
(2)如图2,
∵DF2=FM FC,
∴,
∵∠DFM=∠CFD,
∴△DFM∽△CFD,
∴∠FDM=∠FCD,
∵∠CAD=∠BCF,
∴∠FDM=∠CAD,
∴DF∥AC.
7.如图,△ABC中,AB=AC.
(1)尺规作图:作AB的垂直平分线DE,分别交AB、AC于点E和点D.(保留作图痕迹,不写作法);
(2)连接BD,若BD=BC=2,求AC的长.
(3)在(2)的条件下,cosC= .
【分析】(1)根据要求作出图形即可;
(2)求出证明∠A=36°,再利用相似三角形的性质证明即可;
(3)过点B作BH⊥CD于点H.求出CH,可得结论.
【解答】解:(1)如图,直线DE即为所求;
(2)如图,
∵点D在AB的垂直平分线上,
∴DA=DB,
∴∠A=∠DBA,
∵BD=BC,
∴∠BDC=∠C,
∵∠BDC=∠A+∠DBA=2∠A,
∴∠C=2∠A,
∵AB=AC,
∴∠ABC=∠C=2∠A,
∵∠A+∠ABC+∠C=180°,
∴5∠A=180°,
∴∠A=36°,
∴∠CBD=∠ABD=∠A=36°,
∵∠C=∠C,
∴△CBD∽△CAB,
∴CB2=CD CA,
∴22=CD (CD+2),
∴CD=﹣1(负值已经舍去),
∴AC=CD+AD=+1;
(3)过点B作BH⊥CD于点H.
∵BC=BD,BH⊥CD,
∴CH=DH=,
∴cocC==.
故答案为:.
8.如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边与AB交于点E.
(1)求证:Rt△AEP∽Rt△DPC;
(2)当∠CPD=30°时,求AE的长.
【分析】(1)利用“一线三直角”模型,即可证明Rt△AEP∽Rt△DPC;
(2)由矩形的性质结合已知条件得出CD=AB=4,利用含30度角的直角三角形的性质得出PC=8,利用勾股定理求出PD的长度,进而求出AP的长度,再利用相似三角形的性质即可求出AE的长.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠D=∠A=90°,
∴∠PCD+∠DPC=90°,
∵∠CPE=90°,
∴∠EPA+∠DPC=90°,
∴∠PCD=∠EPA,
∴Rt△AEP∽Rt△DPC;
(2)解:∵四边形ABCD是矩形,AB=4,
∴CD=AB=4,
在Rt△PCD中,∠CPD=30°,CD=4,
∴PC=8,
∴,
∴,
∵Rt△AEP∽Rt△DPC,
∴,即,
∴.
9.如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
【分析】(1)根据矩形的性质可得AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,根据垂直定义可得∠FAE=90°,从而可得∠BAF=∠DAE,进而可得△ABF∽△ADE,然后利用相似三角形的性质可得=,再利用两边成比例且夹角相等的两个三角形相似证明,即可解答;
(2)根据角平分线的定义可得∠AFE=∠CFE,从而证明△AFE≌△CFE,进而可得AF=CF,AE=EC,然后再证△AFG≌△CFG,从而可得∠FAG=∠FCG,再结合(1)的结论可得∠DAE=∠FCG,最后利用等角的余角相等可得∠DCG=∠AED,从而可得AE∥CG,进而利用菱形的判定方法即可解答.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,
∴∠ABF=180°﹣∠ABC=90°,
∵AE⊥AF,
∴∠FAE=90°,
∴∠FAE﹣∠BAE=∠DAB﹣∠BAE,
∴∠BAF=∠DAE,
∵∠D=∠ABF=90°,
∴△ABF∽△ADE,
∴=,
∴=,
∵∠D=∠FAE=90°,
∴△AEF∽△DAC;
(2)如图:
∵FE平分∠AFB,
∴∠AFE=∠CFE,
∵∠FAE=∠BCD=90°,EF=EF,
∴△AFE≌△CFE(AAS),
∴AF=CF,AE=EC,
∵FG=FG,
∴△AFG≌△CFG(SAS),
∴∠FAG=∠FCG,
∵∠BAF=∠DAE,
∴∠DAE=∠FCG,
∵∠DAE+∠AED=90°,∠BCG+∠DCG=90°,
∴∠DCG=∠AED,
∴AE∥CG,
∵AB∥CD,
∴四边形AGCE是平行四边形,
∵AE=EC,
∴四边形AGCE为菱形.
10.已知:如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,点F在边AD上,CF交BD于点G,CF∥AE,CF=BD.
(1)求证:四边形AECF为菱形;
(2)如果∠DCG=∠DEC,求证:AE2=AD DC.
【分析】(1)根据直角三角形斜边上的中线可得AE=DE=BD,CE=BD,再结合已知CF=BD,从而可得AE=CF,进而可得四边形AECF是平行四边形,然后再根据AE=CE,即可解答;
(2)利用(1)的结论可得AE=CF=DE,AD∥CE,从而可得∠ADE=∠DEC,进而可得∠ADE=∠DCG,再利用平行线的性质可得∠EAD=∠CFD,然后证明△ADE∽△FCD,利用相似三角形的性质即可解答.
【解答】证明:(1)∵∠BAD=90°,E为BD的中点,
∴AE=DE=BD,
∵CF=BD,
∴AE=CF=DE,
∵CF∥AE,
∴四边形AECF是平行四边形,
∵∠BCD=90°,E为BD的中点,
∴CE=BD,
∴AE=CE,
∴四边形AECF为菱形;
(2)∵四边形AECF为菱形,
∴AD∥CE,
∴∠ADE=∠DEC,
∵∠DCG=∠DEC,
∴∠ADE=∠DCG,
∵AE∥CF,
∴∠EAD=∠CFD,
∴△ADE∽△FCD,
∴=,
∴CF DE=AD CD,
∵AE=CF=DE,
∴AE2=AD DC.
11.如图,在矩形ABCD中,AB=3,BC=5,BE平分∠ABC交AD于点E.连接CE,点F是BE上一动点,过点F作FG∥CE交BC于点G.将△BFG绕点B旋转得到△BF'G'.
(1)连接CG',EF',求证:△BEF'∽△BCG';
(2)当点G'恰好落在直线AE上时,若BF=3,求EG'的值.
【分析】(1)可证得∠F′BE=∠CBG′,=,从而证明了结论;
(2)先求得BG的长,进而求得BG′,然后解直角三角形ABG′求得结果.
【解答】(1)证明:∵FG∥CE,
∴△BFG∽△BEC,
∴=,
∴=,
∵∠F′BG′=∠EBC,
∴∠FBG′+∠EBG′=∠EBC+∠EBG′,
即∠F′BE=∠CBG,
∴△BEF′∽△BCG′;
(2)如图1,
∵四边形ABCD是矩形,
∴∠D=∠A=∠ABC=90°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=45°,
∴∠AEB=90°﹣∠ABE=45°,
∴∠AEB=∠ABE,
∴AE=AB=3,
∴BE=3,
由(1)知:=,
∴=,
∴BG=,
∴BG′=BG=,
在Rt△ABG′中,由勾股定理得,
AG′===,
∴EG′=AE﹣AG′=3﹣=,
EG″=,
综上所述:EG′=.
12.如图,正方形ABCD,E、F分别是边AB,BC的中点,AF与DE,DB分别交于点M,N.
(1)求证:AF=DE,AF⊥DE.
(2)求AM:MN:NF的值.
【分析】(1)根据SAS证明△ADE≌△BAF,即可得AF=DE,∠ADE=∠BAF,故∠ADE+∠AED=∠BAF+∠AED=90°,AF⊥DE;
(2)设正方形ABCD的边长为2x,则AE=BF=x,由勾股定理和面积法可得AM==x,证明△NAD∽△NFB,可得NF=AF=x,即可得到答案.
【解答】(1)证明:∵正方形ABCD,
∴AB=DA,∠ABC=∠BAD=90°,
∵E、F为边AB、BC的中点,
∴BF=AE,
在△ADE与△BAF中,
,
∴△ADE≌△BAF(SAS),
∴AF=DE,∠ADE=∠BAF,
∴∠ADE+∠AED=∠BAF+∠AED=90°,
∴∠AME=90°,
∴AF⊥DE;
(2)解:设正方形ABCD的边长为2x,则AE=BF=x,
在Rt△ADE中,DE==x,
由(1)知DE=AF,
∴AF=x,
∵2S△ADE=AE AD=DE AM,
∴AM==x,
∵AD∥BC,
∴∠ADN=∠NBF,∠NAD=∠NFB,
∴△NAD∽△NFB,
∴==2,
∴AN=2FN,
∴NF=AF=x,
∴MN=AF﹣AM﹣NF=,
∴AM:MN:NF=x:x:x=6:4:5.
13.问题背景
如图1,在△ABC中,点D,E分别在AC,AB上,2∠EDB+∠BDC=180°,∠DEB=90°,求证:AE=BE.
变式迁移
如图2,在四边形DEBC中,2∠EDB+∠BDC=180°,∠DEB=90°,DF∥EB,DF分别交CE,BC于点G,F,求证:DG=FG.
拓展应用
如图3,在四边形DECB中,2∠DBE+∠EBC=180°,∠EDB=∠DCB,,且n>1,直接写出的值.
【分析】问题背景:由2∠EDB+∠BDC=180°,∠ADB+∠BDC=180°,得出∠ADE=∠EDB,由∠DEB=90°,得出∠DEA=∠DEB=90°,即可得出△DEA≌△DEB,进而证明AE=BE;
变式迁移:延长CD,BE交于点M,则ME=BE,由DF∥BE,得出△CDG∽△CME,△CFG∽△CBE,进而得出,即可证明DG=FG;
拓展应用:在CB的延长线上截取BP=BE,连接DP,由“问题背景”可知:∠DBP=∠DBE,进而得出△DBE≌△DBP,得出∠EDB=∠PDB,由∠EDB=∠DCB,得出∠PDB=∠DCB,继而证明△DPB∽△CPD,得出===,设BP=1,则PD=n,得出PC=n2,求出BC=n2﹣1,继而得出=n2﹣1.
【解答】问题背景:证明:如图1,
∵2∠EDB+∠BDC=180°,∠ADB+∠BDC=180°,
∴∠ADB=2∠EDB,
∴∠ADE+∠EDB=2∠EDB,
∴∠ADE=∠EDB,
∵∠DEB=90°,
∴∠DEA=∠DEB=90°,
在△DEA和△DEB中,
,
∴△DEA≌△DEB(ASA),
∴AE=BE;
变式迁移:证明:如图2,延长CD,BE交于点M,则ME=BE,
∵DF∥BE,
∴∠CDG=∠M,∠CGD=∠CEM,∠CGF=∠CEB,∠CFG=∠CBE,
∴△CDG∽△CME,△CFG∽△CBE,
∴,,
∴,
∵ME=BE,
∴DG=FG;
拓展应用:解:如图3,在CB的延长线上截取BP=BE,连接DP,
由“问题背景”可知:∠DBP=∠DBE,
在△DBE和△DBP中,
,
∴△DBE≌△DBP(SAS),
∴∠EDB=∠PDB,
∵∠EDB=∠DCB,
∴∠PDB=∠DCB,
∵∠P=∠P,
∴△DPB∽△CPD,
∴==,
∵,
∴===,
设BP=1,则PD=n,
∴,
∴PC=n2,
∴BC=PC﹣BP=n2﹣1,
∴===n2﹣1.
14.问题提出
(1)如图①正三角形ABC,边长为4,D、E是边AB、AC的中点,P在BC边上,则△PDE的面积为 2 ;
问题解决
(2)如图②,某小区有一块五边形空地ABCDE,CD⊥DE,AE∥CD,CB=CD=40m,AE=10米,∠ABC=∠BCD=120°,物业想在这块空地中划出一块△MNP区域来种植草皮,其他区域种植花卉.已知种植花卉每平方米200元,种植草皮每平方米100元.要求M,N,P分别位于AB,ED,CD边上,且MN∥CD,要使种植费用的造价最低,种植草皮的△MNP的面积应该满足什么条件?并求出费用的最小值.
【分析】(1)过点A作AH⊥BC于H,根据三角函数求出AH,由中位线定理得出DE的长度,再根据三角形面积公式求出面积即可;
(2)延长AB交DC延长线于点G,要使种植费用最低,则种植草皮的面积最大,即△MNP面积最大,作MF⊥DC于点F,设QH=m,用m的代数式表示出△MNP的面积,利用二次函数的性质求最值即可.
【解答】解:(1)过点A作AH⊥BC于H,
∵△ABC是等边三角形,D、E是边AB、AC的中点,
∴DE∥BC,DE=BC=2,
∵AH=tan∠ABC AB=4,
∴△PDE的高为AH=2,
∴△PDE的面积为×2×2=2,
故答案为:2;
(2))延长AB交DC延长线于点G,
要使种植费用最低,则种植草皮的面积最大,即△MNP面积最大,
作MF⊥DC于点F,
∵∠ABC=∠BCD=120°,
∴∠GBC=∠BCG=60°,
∴△GBC为等边三角形,
即GC=BC=40m,GD=GC+CD=80m,
作MF⊥CD于F,设GF=x,
则MF=GF tan60°=x,
∵MN∥CD,MF⊥CD,ND⊥CD,
∴四边形MNDF是矩形,
∴MN=FD=GD﹣GF=80﹣m,
∴S△MNP=(80﹣m)×m=﹣(m﹣40)2+800,
∵﹣<0,
∴当m=40时,△MNP的面积最大为800,
作AQ⊥MN于Q,则MQ=MN﹣NQ=MN﹣AE=80﹣40﹣10=30,
∴AQ=MQ tan60°=30,
此时花卉种植面积为S梯形AEDG﹣S△BCG﹣S△MNP=(10+80)×(30+40)﹣×40×20﹣800=1950,
∴总费用为800×100+1950×200=470000(元),
即要使种植费用的造价最低,种植草皮的△MNP的面积最大,费用的最小值为470000元.
15.如图,在正方形ABCD中,点E在BC边上,连接AE,在BC延长线上作EF=AE,连接AF交CD于点G,设CE:EB=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若G点为CD的中点,①求证:EG⊥AF.②求λ的值.
【分析】(1)根据AB=2,λ=1,可以得到BE、CE的长,然后根据正方形的性质,可以得到AE的长,再根据平行线的性质和角平分线的性质,可以得到EF的长,从而可以得到线段CF的长;
(2)①要证明点G为CD边的中点,只要证明△ADG≌△FGC即可,然后根据题目中的条件,可以得到△ADG≌△FGC的条件,从而可以证明结论成立;
②根据题意和三角形相似,可以得到CE和EB的比值,从而可以得到λ的值.
【解答】解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE==,
∴EF=,
∴CF=EF﹣EC=﹣1;
(2)①证明:∵EA=EF,点G为CD的中点,
∴DG=CG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴AG=FG,
∵AE=EF,
∴EG⊥AF;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴△EGC∽△GFC,
∴=,
∵GC=a,FC=2a,
∴=,
∴=,
∴EC=a,BE=BC﹣EC=2a﹣a=a,
∴λ===.
16.如图,已知△ABC,点D,E分别在BC,CA上,且满足AD=AB,EB=EC.
(1)用直尺和圆规确定点D,E;(保留作图痕迹,不写作法)
(2)连接AD,EB,AD与EB交于点F.
①求证:△BDF∽△CBA;
②若∠BAC=90°,AB=3,AC=4,则DF的长为 .
【分析】(1)以A点为圆心AB长为半径画弧交BC于点D,作BC的垂直平分线交AC于E即可;
(2)①根据等腰三角形的性质得出两组对应角相等即可证明三角形相似;
②过点A作AH⊥BD于点H,根据勾股定理求出BC的长度,刘勇三角函数求出BH,根据等腰三角形的性质得出BD,再根据相似三角形对应边成比例求出DF即可.
【解答】解:(1)作图如下:
(2)①如下图:
∵AB=AD,
∴∠ABD=∠ADB,
∵EB=EC,
∴∠EBD=∠C,
∴△BDF∽△CBA;
②过点A作AH⊥BD于点H,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵cos∠ABH=,
∴=,
∴BH=,
∵AB=AD,
∴BD=2BH=,
由①知△BDF∽△CBA,
∴,
即,
解得DF=,
故答案为:.
17.如图,△ABC是等腰直角三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,DE⊥DF,∠DEF=45°,DF的延长线与BC的延长线相交于点G.
(1)求证:△BDE∽△CEF;
(2)若AD=1,AF=2,求EC的长;
(3)若,求的值.
【分析】(1)根据已知可得∠B=∠C=45°,再根据∠DEF=45°,然后利用一线三等角模型证明,即可解答;
(2)过点E作EH⊥AB,垂足为H,根据已知可得DE=DF,然后证明一线三等角模型全等△ADF≌△HED,从而可得AD=EH=1,AF=DH=2,进而可求出BH,BE,AB,BC的长,进行计算即可解答;
(3)过点C作MC⊥AC,交DG于点M,可得AB∥CM,根据已知在Rt△DHE中,设EH=m,则DH=2m,利用(2)的结论可得EH=AD=BH=m,DH=AF=2m,BE=BH=m,从而求出BE,BC,CF的长,进而可得AF=CF,然后证明△ADF≌△CMF,利用全等三角形的性质可得AD=CM=m,最后证明△BDG∽△CMG,利用相似三角形的性质进行计算可求出CG的长,从而求出EG的长,即可解答.
【解答】(1)证明:∵AB=AC,∠A=90°,
∴∠B=∠C=45°,
∴∠BDE+∠BED=180°﹣∠B=135°,
∵∠DEF=45°,
∴∠BED+∠FEG=180°﹣∠DEF=135°,
∴∠BDE=∠FEG,
∴△BDE∽△CEF;
(2)过点E作EH⊥AB,垂足为H,
∵DE⊥DF,
∴∠EDF=90°,
∵∠DEF=45°,
∴DE=DF,
∵∠ADF+∠EDB=90°,∠ADF+∠AFD=90°,
∴∠AFD=∠EDB,
∵∠A=∠EHD=90°,
∴△ADF≌△HED(AAS),
∴AD=EH=1,AF=DH=2,
∵∠BHE=90°,∠B=45°,
∴BH=HE=1,
∴BE=BH=,AB=AD+DH+BH=4,
∵BC=AB=4,
∴EC=BC﹣BE=3;
(3)过点C作MC⊥AC,交DG于点M,
∴∠A=∠MCA=90°,
∴CM∥AB,
在Rt△DHE中,,
∴=,
设EH=m,则DH=2m,
由(2)得:EH=AD=BH=m,DH=AF=2m,BE=BH=m,
∴AC=AB=AD+DH+BH=4m,
∴BC=AB=4m,CF=AC﹣AF=4m﹣2m=2m,
∴AF=CF,
∵∠A=∠MCF=90°,∠AFD=∠MFC,
∴△ADF≌△CMF(ASA),
∴AD=CM=m,
∵CM∥AB,
∴∠B=∠MCG,∠BDG=∠CMG,
∴△BDG∽△CMG,
∴=,
∴=,
∴CG=2m,
∴EG=BC+CG﹣BE=5m,
∴==5,
∴的值为5.
18.如图,在正方形ABCD中,点E是边AD上的一点(不与A、D重合),点F在边DC延长线上,CF=AE,连接BE、BF、EF,EF交BC于点M,交对角线BD于N.
(1)求证:∠BEF=45°;
(2)若BE平分∠ABD,求证:BE2=AB BM;
(3)若DE:EA=3:2,则EN:NM:MF= 21:29:20 (直接写答案).
【分析】(1)先证明△ABD≌△BCF,进而便可得∠BEF的度数;
(2)证明BD=AB,再证明△EBD∽△MBF,得BE BF=BD MB,进而便可得出结论;
(3)设正方形ABCD的边长为a,用a表示AE、CF、DE,证明△FMC∽△MED,用a表示CM,进而用a表示BM,再证明△EDN∽△MBN,便可求得EN:MN,进而便可求得结果.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°=∠BCF,
∵AE=CF,
∴△ABD≌△BCF(SAS),
∴BE=BF,∠ABE=∠CBF,
∴∠ABF=∠EBC+CBF=∠EBC+∠ABE=∠ABC=90°,
∴∠BEF=∠BFE=45°;
(2)证明:由(1)知,∠BFE=∠BEF=45°,BE=BF,
∵四边形ABCD是正方形,
∴∠EDB=∠ABD=45°,∠ABC=90°,
∴BD=AB,
∵BE平分∠ABD,
∴∠ABE=∠EBD,
∴∠CBF=90°﹣∠EBC=∠ABE=∠EBD,
∵∠EDB=∠NFB=45°,
∴△EBD∽△MBF,
∴,
∴BE BF=BD MB,
∵BE=BF,BD=AB,
∴;
(3)解:设正方形ABCD的边长为a,
∵DE:EA=3:2,
∴AE=AD=,DE=a,
∴CF=AE==,
∵CD=AD=a,
∴CF:DF=2:7,
∵CM∥DE,
∴△FMC∽△FED,
∴=,
∴CM=DE=,
∴BM=BC﹣CM=a﹣=a,
∵DE∥BM,
∴△EDN∽△MBN,
∴,
设EN=21k,则MN=29k,
∵,
∴MF=,
∴MF=20k,
∴EN:NM:MF=21k:29k:20k=21:29:20.
故答案为:21:29:20.
19.如图1,在四边形ABCD中,∠ABC=∠BCD,过点A作AE∥DC交BC边于点E,过点E作EF∥AB交CD边于点F,连接AF,过点C作CH∥AF交AE于点H,连接BH.
(1)求证:△ABH≌△EAF;
(2)如图2,若BH的延长线经过AF的中点M,求的值.
【分析】(1)由∠ABC=∠BCD和AE∥DC可得AB=AE,由EF∥AB可得∠BAH=∠AEF,由AE∥DC,CH∥AF可得四边形AHCF为平行四边形,从而可得AH=CF,再由EF∥AB可得∠ABC=∠CEF,从而可得EF=CF,即可得出EF=AH,即可证明;
(2)延长BM,EF交于点G,由EF∥AB可得∠ABE=∠FEC,由AE∥CF可得∠AEB=∠FCE,从而可得△ABE∽△FEC,设EF=CF=a,AB=AE=ax,由点M为AF中点可得AM=FM,由EF∥AB可得∠ABM=∠FGM,可证△ABM≌△FGM(AAS),则FG=AB=ax,则EG=EF+FG=a+ax,由(1)可知四边形AHCF为平行四边形,可得AH=CF=a,则EH=AE﹣AH=ax﹣a,由AB∥EG可得△ABH∽△EGH,从而可得=,即=,解得x=1±,由x>0可得x=1+,即=x=1+.
【解答】(1)证明:∵AE∥DC,
∵∠AEB=∠BCD,
∵∠ABC=∠BCD,
∴∠AEB=∠ABC,
∴AB=AE,
∵EF∥AB,
∴∠BAH=∠AEF,
∵AE∥DC,CH∥AF,
∴四边形AHCF为平行四边形,
∴AH=CF,
∵EF∥AB,
∴∠ABC=∠CEF,
∵AE∥CF,
∴∠ECF=∠AEB=∠ABC,
∴∠ECF=∠CEF,
∴EF=CF,
∴EF=AH,
∴△ABH≌△EAF(SAS);
(2)如图,延长BM,EF交于点G,
∵EF∥AB,
∴∠ABE=∠FEC,
∵AE∥CF,
∴∠AEB=∠FCE,
∴△ABE∽△FEC,
设EF=CF=a,AB=AE=ax,
∵点M为AF中点
∴AM=FM,
∵EF∥AB
∴∠ABM=∠FGM,
∴△ABM≌△FGM(AAS),
FG=AB=ax,
∴EG=EF+FG=a+ax,
由(1)可知四边形AHCF为平行四边形,
∴AH=CF=a,
∴EH=AE﹣AH=ax﹣a,
∵AB∥EG
∴△ABH∽△EGH,
∴=,
即=,
解得x=1±,
∵x>0,
∴x=1+,
即=x=1+.
20.如图1,在矩形ABCD中,AB=5,AD=8,点E在边CD上,tan∠BAE=2,点F是线改AE上一点,连接CF.
(1)连接BF,请用尺规作图法作FG⊥AB,垂足为G点(保留作图痕迹,不要求写出作法).若tan∠ABF=,求线段AF的长.
(2)如图2,若CF=BC,AE的延长线与BC的延长线交于点H,求△CEF的面积.
【分析】(1)根据垂线的画法画图即可;设AG=x,则BG=5﹣x,在Rt△AFG中,tan∠BAE==2,可得FG=2x,在Rt△BFG中,tan∠ABF=,求得x=2,由勾股定理可得AF=,即可得出答案.
(2)过点C作CM⊥AH于点M,在Rt△ABH中,tan∠BAE==2,可得BH=10,CH=BH﹣BC=2,根据AB∥CD,可得∠CEH=∠BAE,则tan∠CEH==2,可得CE=1,在Rt△CEM中,tan∠CEM==2,设EM=a,则CM=2a,由勾股定理可得CE2=EM2+CM2,即可求得a=,则CM=,在Rt△CFM中,CF=BC=2,由勾股定理可得FM==,进而可得EF=FM﹣EM=,则根据EF CM可得出答案.
【解答】解:(1)如图,FG即为所求.
设AG=x,则BG=5﹣x,
在Rt△AFG中,
tan∠BAE==2,
∴FG=2x,
在Rt△BFG中,
tan∠ABF=,
解得x=2,
∴AG=2,FG=4,
AF==2.
(2)过点C作CM⊥AH于点M,
在Rt△ABH中,
tan∠BAE==2,
∴BH=10,
则CH=BH﹣BC=2,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠CEH=∠BAE,
则tan∠CEH==2,
∴CE=1,
在Rt△CEM中,tan∠CEM==2,
设EM=a,则CM=2a,
由勾股定理可得CE2=EM2+CM2,
即a2+(2a)2=12,
解得a=,
∴CM=,
在Rt△CFM中,CF=BC=2,
由勾股定理可得FM==,
∴EF=FM﹣EM=.
∴EF CM=.
1.如图,E是菱形ABCD对角线AC上一点,四边形BGFE是矩形.点F,G分别在DC,BC上.
(1)求证:∠CFG=∠ABE.
(2)若BE=4,,求FM的长.
2.如图,在 ABCD中,AE⊥BC于点E,点F在BC的延长线上,且CF=BE,连接AC,DF.
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,AE=4,CF=2,求.
3.如图,已知正方形ABCD的边长为a,正方形CEFG的边长为b(b<a),点E在CD边上,点G在BC延长线上,点H为BC上的点,连接DF,DH.
(1)当DH⊥DF时,求证:△DEF∽△HCD.
(2)若点H为BC的中点,在(1)的条件下,求出a与b满足的关系式.
4.已知:如图,在四边形ABCD中,AD∥BC,点E、F分别在边AB、AD上,DE与CF相交于点G.CD2=CG CF,∠AED=∠CFD.
(1)求证:AB=CD;
(2)延长AD至点M,联结CM,当CF=CM时,求证:EA AB=AD MD.
5.北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“弦图”,该图被誉为“中国数学界的图腾”,它是由四个直角三角形与中间的小正方形拼成的一个大正方形.
如图为“弦图”的一部分,在正方形ABCD中,DE⊥AF,BF⊥AF.
(1)求证:EF=DE﹣BF;
(2)连接BE,若BF2=EF DE,求证:∠1=∠2.
6.如图,已知:△ABC和△ADE都是等边三角形,其中点D在边BC上,点F是AB边上一点,且BF=CD.
(1)求证:DE∥CF;
(2)联结DF,设AD、CF的交点为M,如果DF2=FM FC,求证:DF∥AC.
7.如图,△ABC中,AB=AC.
(1)尺规作图:作AB的垂直平分线DE,分别交AB、AC于点E和点D.(保留作图痕迹,不写作法);
(2)连接BD,若BD=BC=2,求AC的长.
(3)在(2)的条件下,cosC= .
8.如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边与AB交于点E.
(1)求证:Rt△AEP∽Rt△DPC;
(2)当∠CPD=30°时,求AE的长.
9.如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
10.已知:如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,点F在边AD上,CF交BD于点G,CF∥AE,CF=BD.
(1)求证:四边形AECF为菱形;
(2)如果∠DCG=∠DEC,求证:AE2=AD DC.
11.如图,在矩形ABCD中,AB=3,BC=5,BE平分∠ABC交AD于点E.连接CE,点F是BE上一动点,过点F作FG∥CE交BC于点G.将△BFG绕点B旋转得到△BF'G'.
(1)连接CG',EF',求证:△BEF'∽△BCG';
(2)当点G'恰好落在直线AE上时,若BF=3,求EG'的值.
12.如图,正方形ABCD,E、F分别是边AB,BC的中点,AF与DE,DB分别交于点M,N.
(1)求证:AF=DE,AF⊥DE.
(2)求AM:MN:NF的值.
13.问题背景
如图1,在△ABC中,点D,E分别在AC,AB上,2∠EDB+∠BDC=180°,∠DEB=90°,求证:AE=BE.
变式迁移
如图2,在四边形DEBC中,2∠EDB+∠BDC=180°,∠DEB=90°,DF∥EB,DF分别交CE,BC于点G,F,求证:DG=FG.
拓展应用
如图3,在四边形DECB中,2∠DBE+∠EBC=180°,∠EDB=∠DCB,,且n>1,直接写出的值.
14.问题提出
(1)如图①正三角形ABC,边长为4,D、E是边AB、AC的中点,P在BC边上,则△PDE的面积为 ;
问题解决
(2)如图②,某小区有一块五边形空地ABCDE,CD⊥DE,AE∥CD,CB=CD=40m,AE=10米,∠ABC=∠BCD=120°,物业想在这块空地中划出一块△MNP区域来种植草皮,其他区域种植花卉.已知种植花卉每平方米200元,种植草皮每平方米100元.要求M,N,P分别位于AB,ED,CD边上,且MN∥CD,要使种植费用的造价最低,种植草皮的△MNP的面积应该满足什么条件?并求出费用的最小值.
15.如图,在正方形ABCD中,点E在BC边上,连接AE,在BC延长线上作EF=AE,连接AF交CD于点G,设CE:EB=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若G点为CD的中点,①求证:EG⊥AF.②求λ的值.
16.如图,已知△ABC,点D,E分别在BC,CA上,且满足AD=AB,EB=EC.
(1)用直尺和圆规确定点D,E;(保留作图痕迹,不写作法)
(2)连接AD,EB,AD与EB交于点F.
①求证:△BDF∽△CBA;
②若∠BAC=90°,AB=3,AC=4,则DF的长为 .
17.如图,△ABC是等腰直角三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,DE⊥DF,∠DEF=45°,DF的延长线与BC的延长线相交于点G.
(1)求证:△BDE∽△CEF;
(2)若AD=1,AF=2,求EC的长;
(3)若,求的值.
18.如图,在正方形ABCD中,点E是边AD上的一点(不与A、D重合),点F在边DC延长线上,CF=AE,连接BE、BF、EF,EF交BC于点M,交对角线BD于N.
(1)求证:∠BEF=45°;
(2)若BE平分∠ABD,求证:BE2=AB BM;
(3)若DE:EA=3:2,则EN:NM:MF= (直接写答案).
19.如图1,在四边形ABCD中,∠ABC=∠BCD,过点A作AE∥DC交BC边于点E,过点E作EF∥AB交CD边于点F,连接AF,过点C作CH∥AF交AE于点H,连接BH.
(1)求证:△ABH≌△EAF;
(2)如图2,若BH的延长线经过AF的中点M,求的值.
20.如图1,在矩形ABCD中,AB=5,AD=8,点E在边CD上,tan∠BAE=2,点F是线改AE上一点,连接CF.
(1)连接BF,请用尺规作图法作FG⊥AB,垂足为G点(保留作图痕迹,不要求写出作法).若tan∠ABF=,求线段AF的长.
(2)如图2,若CF=BC,AE的延长线与BC的延长线交于点H,求△CEF的面积.
参考答案与试题解析
1.如图,E是菱形ABCD对角线AC上一点,四边形BGFE是矩形.点F,G分别在DC,BC上.
(1)求证:∠CFG=∠ABE.
(2)若BE=4,,求FM的长.
【分析】(1)根据菱形的性质可得AB∥CD,从而可得∠CAB=∠DCA,根据矩形的性质可得BE∥FG,从而可得∠BEM=∠FME,然后利用三角形的外角可得∠BEM=∠BAE+∠ABE,∠FME=∠ACD+∠CFG,即可解答;
(2)根据矩形的性质可得EB=FG=4,∠EFG=∠FGB=90°,EF∥BG,再利用(1)的结论在Rt△FGC中,利用锐角三角函数的定义和勾股定理求出CG,CF的长,根据菱形的性质可得AD∥BC,AD=DC,从而可得AD∥EF,∠DAC=∠DCA,进而可得∠FEC=∠DCA,然后利用等角对等边可得FE=FC=5,最后证明8字模型相似三角形△EFM∽△CGM,利用相似三角形的性质进行计算即可解答.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠CAB=∠DCA,
∵四边形BGFE是矩形,
∴BE∥FG,
∴∠BEM=∠FME,
∵∠BEM=∠BAE+∠ABE,∠FME=∠ACD+∠CFG,
∴∠CFG=∠ABE;
(2)解:∵四边形BGFE是矩形,
∴EB=FG=4,∠EFG=∠FGB=90°,EF∥BG,
∴∠FGC=180°﹣∠FGB=90°,
∵,∠CFG=∠ABE,
∴tan∠CFG=,
∴CG=FG tan∠CFG=4×=3,
∴FC===5,
∵四边形ABCD是菱形,
∴AD∥BC,AD=DC,
∴AD∥EF,
∴∠DAC=∠FEC,
∵AD=DC,
∴∠DAC=∠DCA,
∴∠FEC=∠DCA,
∴FE=FC=5,
∵∠EFG=∠FGC=90°,∠EMF=∠CMG,
∴△EFM∽△CGM,
∴=,
∴=,
∴FM=,
∴FM的长为.
2.如图,在 ABCD中,AE⊥BC于点E,点F在BC的延长线上,且CF=BE,连接AC,DF.
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,AE=4,CF=2,求.
【分析】(1)先证明四边形AEFD是平行四边形,再证明∠AEF=90°即可;
(2)根据矩形的性质和相似三角形的判定和性质解答即可.
【解答】(1)证明:∵CF=BE,
∴CF+EC=BE+EC.
即 EF=BC.
在 ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD=EF.
∴四边形AEFD是平行四边形.
∵AE⊥BC,
∴∠AEF=90°.
∴四边形AEFD是矩形;
(2)解:∵四边形AEFD是矩形,
∴∠AEC=∠DFC=90°,AE=DF=4,
∴∠EAC+∠ECA=90°,
∵∠ACD=90°,
∴∠ECA+∠DCF=90°,
∴∠EAC=∠DCF,
∴△AEC∽△CFD,
∴==,
∴EC=2AE=8,
解法一:∴===4.
解法二:∴=()2=()2=4.
3.如图,已知正方形ABCD的边长为a,正方形CEFG的边长为b(b<a),点E在CD边上,点G在BC延长线上,点H为BC上的点,连接DF,DH.
(1)当DH⊥DF时,求证:△DEF∽△HCD.
(2)若点H为BC的中点,在(1)的条件下,求出a与b满足的关系式.
【分析】(1)证明∠EDF=∠DHC,再结合90°角可以证明△DEF∽△HCD;
(2)根据(1)中的相似得到对应边成比例,可以得到关于a和b的等式即可得解.
【解答】(1)证明:∵四边形ABCD,CEFG都是正方形,
∴∠HCD=90°,∠CEF=∠DEF=90°,
∴∠DEF=∠HCD=90°,
∴∠HDC+∠DHC=90°,
又∵DH⊥DF,
∴∠HDF=90°,
∴∠HDC+∠EDF=90°,
∴∠EDF=∠DHC,
∴△DEF∽△HCD.
(2)解:∵点H为BC的中点,
∴HC=,
∵CD=a,CE=EF=b,∴DE=a﹣b,
由(1)可知△DEF∽△HCD,
∴,
∴,
∴,
即a与b满足的关系式为a=.
4.已知:如图,在四边形ABCD中,AD∥BC,点E、F分别在边AB、AD上,DE与CF相交于点G.CD2=CG CF,∠AED=∠CFD.
(1)求证:AB=CD;
(2)延长AD至点M,联结CM,当CF=CM时,求证:EA AB=AD MD.
【分析】(1)根据已知可得=,从而可得△CDG∽△CFD,然后利用相似三角形的性质可得∠CDG=∠CFD,从而可得∠CDG=∠AED,进而可得AB∥CD,最后证明四边形ABCD是平行四边形,从而利用平行四边形的性质即可解答;
(2)根据等腰三角形的性质可得∠CFD=∠M,从而可得∠AED=∠M,然后利用平行线的性质可得∠A=∠CDM,从而可证△AED∽△DMC,进而利用相似三角形的性质即可解答.
【解答】证明:(1)∵CD2=CG CF,
∴=,
∵∠DCG=∠DCF,
∴△CDG∽△CFD,
∴∠CDG=∠CFD,
∵∠AED=∠CFD,
∴∠CDG=∠AED,
∴AB∥CD,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∴AB=CD;
(2)如图:
∵CF=CM,
∴∠CFD=∠M,
∵∠AED=∠CFD,
∴∠AED=∠M,
∵AB∥CD,
∴∠A=∠CDM,
∴△AED∽△DMC,
∴=,
∴AE DC=AD DM,
∵AB=DC,
∴EA AB=AD MD.
5.北京召开的国际数学家大会会标取材于我国古代数学家赵爽的“弦图”,该图被誉为“中国数学界的图腾”,它是由四个直角三角形与中间的小正方形拼成的一个大正方形.
如图为“弦图”的一部分,在正方形ABCD中,DE⊥AF,BF⊥AF.
(1)求证:EF=DE﹣BF;
(2)连接BE,若BF2=EF DE,求证:∠1=∠2.
【分析】(1)利用正方形的性质可得AB=AD,∠BAD=90°,从而可得∠BAF+∠DAE=90°,根据垂直定义可得∠AED=∠F=90°,从而可得∠BAF+∠ABF=90°,然后利用同角的余角相等可得∠DAE=∠ABF,从而可证△ABF≌△DAE,D进而可得DE=AF,AE=BF,即可解答;
(2)利用(1)的结论可得DE=AF,∠BAF=∠ADE=∠2,从而可得=,进而可得△FBE∽△FAB,然后利用相似三角形的性质可得∠1=∠BAF,即可解答.
【解答】证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAF+∠DAE=90°,
∵DE⊥AF,BF⊥AF,
∴∠AED=∠F=90°,
∴∠BAF+∠ABF=90°,
∴∠DAE=∠ABF,
∴△ABF≌△DAE(AAS),
∴DE=AF,AE=BF,
∵EF=AF﹣AE,
∴EF=DE﹣BF;
(2)∵△ABF≌△DAE,
∴DE=AF,∠BAF=∠ADE=∠2,
∵BF2=EF DE,
∴=,
∴=,
∵∠F=∠F,
∴△FBE∽△FAB,
∴∠1=∠BAF,
∴∠1=∠2.
6.如图,已知:△ABC和△ADE都是等边三角形,其中点D在边BC上,点F是AB边上一点,且BF=CD.
(1)求证:DE∥CF;
(2)联结DF,设AD、CF的交点为M,如果DF2=FM FC,求证:DF∥AC.
【分析】(1)由等边三角形的性质证明△ACD≌△CBF,得出∠CAD=∠BCF,由等边三角形的性质及三角形外角的性质得出∠BDE=∠CAD,进而得出∠BDE=∠BCF,即可证明DE∥CF;
(2)先证明△DFM∽△CFD,得出∠FDM=∠FCD,由∠CAD=∠BCF,得出∠FDM=∠CAD,即可证明DF∥AC.
【解答】证明:(1)如图1,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
在△ACD和△CBF中,
,
∴△ACD≌△CBF(SAS),
∴∠CAD=∠BCF,
∵△ADE是等边三角形,
∴∠ADE=∠ACB=60°,
∵∠ADE+∠BDE=∠ACB+∠CAD,
∴∠BDE=∠CAD,
∴∠BDE=∠BCF,
∴DE∥CF;
(2)如图2,
∵DF2=FM FC,
∴,
∵∠DFM=∠CFD,
∴△DFM∽△CFD,
∴∠FDM=∠FCD,
∵∠CAD=∠BCF,
∴∠FDM=∠CAD,
∴DF∥AC.
7.如图,△ABC中,AB=AC.
(1)尺规作图:作AB的垂直平分线DE,分别交AB、AC于点E和点D.(保留作图痕迹,不写作法);
(2)连接BD,若BD=BC=2,求AC的长.
(3)在(2)的条件下,cosC= .
【分析】(1)根据要求作出图形即可;
(2)求出证明∠A=36°,再利用相似三角形的性质证明即可;
(3)过点B作BH⊥CD于点H.求出CH,可得结论.
【解答】解:(1)如图,直线DE即为所求;
(2)如图,
∵点D在AB的垂直平分线上,
∴DA=DB,
∴∠A=∠DBA,
∵BD=BC,
∴∠BDC=∠C,
∵∠BDC=∠A+∠DBA=2∠A,
∴∠C=2∠A,
∵AB=AC,
∴∠ABC=∠C=2∠A,
∵∠A+∠ABC+∠C=180°,
∴5∠A=180°,
∴∠A=36°,
∴∠CBD=∠ABD=∠A=36°,
∵∠C=∠C,
∴△CBD∽△CAB,
∴CB2=CD CA,
∴22=CD (CD+2),
∴CD=﹣1(负值已经舍去),
∴AC=CD+AD=+1;
(3)过点B作BH⊥CD于点H.
∵BC=BD,BH⊥CD,
∴CH=DH=,
∴cocC==.
故答案为:.
8.如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边与AB交于点E.
(1)求证:Rt△AEP∽Rt△DPC;
(2)当∠CPD=30°时,求AE的长.
【分析】(1)利用“一线三直角”模型,即可证明Rt△AEP∽Rt△DPC;
(2)由矩形的性质结合已知条件得出CD=AB=4,利用含30度角的直角三角形的性质得出PC=8,利用勾股定理求出PD的长度,进而求出AP的长度,再利用相似三角形的性质即可求出AE的长.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠D=∠A=90°,
∴∠PCD+∠DPC=90°,
∵∠CPE=90°,
∴∠EPA+∠DPC=90°,
∴∠PCD=∠EPA,
∴Rt△AEP∽Rt△DPC;
(2)解:∵四边形ABCD是矩形,AB=4,
∴CD=AB=4,
在Rt△PCD中,∠CPD=30°,CD=4,
∴PC=8,
∴,
∴,
∵Rt△AEP∽Rt△DPC,
∴,即,
∴.
9.如图,在矩形ABCD中,点E是边CD上任意一点(点E与点C、D不重合),过点A作AF⊥AE,交边CB的延长线于点F,联结EF交边AB于点G,连接AC.
(1)求证:△AEF∽△DAC;
(2)如果FE平分∠AFB,联结CG,求证:四边形AGCE为菱形.
【分析】(1)根据矩形的性质可得AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,根据垂直定义可得∠FAE=90°,从而可得∠BAF=∠DAE,进而可得△ABF∽△ADE,然后利用相似三角形的性质可得=,再利用两边成比例且夹角相等的两个三角形相似证明,即可解答;
(2)根据角平分线的定义可得∠AFE=∠CFE,从而证明△AFE≌△CFE,进而可得AF=CF,AE=EC,然后再证△AFG≌△CFG,从而可得∠FAG=∠FCG,再结合(1)的结论可得∠DAE=∠FCG,最后利用等角的余角相等可得∠DCG=∠AED,从而可得AE∥CG,进而利用菱形的判定方法即可解答.
【解答】证明:(1)∵四边形ABCD是矩形,
∴AB∥CD,AB=DC,∠BCD=∠DAB=∠ABC=∠D=90°,
∴∠ABF=180°﹣∠ABC=90°,
∵AE⊥AF,
∴∠FAE=90°,
∴∠FAE﹣∠BAE=∠DAB﹣∠BAE,
∴∠BAF=∠DAE,
∵∠D=∠ABF=90°,
∴△ABF∽△ADE,
∴=,
∴=,
∵∠D=∠FAE=90°,
∴△AEF∽△DAC;
(2)如图:
∵FE平分∠AFB,
∴∠AFE=∠CFE,
∵∠FAE=∠BCD=90°,EF=EF,
∴△AFE≌△CFE(AAS),
∴AF=CF,AE=EC,
∵FG=FG,
∴△AFG≌△CFG(SAS),
∴∠FAG=∠FCG,
∵∠BAF=∠DAE,
∴∠DAE=∠FCG,
∵∠DAE+∠AED=90°,∠BCG+∠DCG=90°,
∴∠DCG=∠AED,
∴AE∥CG,
∵AB∥CD,
∴四边形AGCE是平行四边形,
∵AE=EC,
∴四边形AGCE为菱形.
10.已知:如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,点F在边AD上,CF交BD于点G,CF∥AE,CF=BD.
(1)求证:四边形AECF为菱形;
(2)如果∠DCG=∠DEC,求证:AE2=AD DC.
【分析】(1)根据直角三角形斜边上的中线可得AE=DE=BD,CE=BD,再结合已知CF=BD,从而可得AE=CF,进而可得四边形AECF是平行四边形,然后再根据AE=CE,即可解答;
(2)利用(1)的结论可得AE=CF=DE,AD∥CE,从而可得∠ADE=∠DEC,进而可得∠ADE=∠DCG,再利用平行线的性质可得∠EAD=∠CFD,然后证明△ADE∽△FCD,利用相似三角形的性质即可解答.
【解答】证明:(1)∵∠BAD=90°,E为BD的中点,
∴AE=DE=BD,
∵CF=BD,
∴AE=CF=DE,
∵CF∥AE,
∴四边形AECF是平行四边形,
∵∠BCD=90°,E为BD的中点,
∴CE=BD,
∴AE=CE,
∴四边形AECF为菱形;
(2)∵四边形AECF为菱形,
∴AD∥CE,
∴∠ADE=∠DEC,
∵∠DCG=∠DEC,
∴∠ADE=∠DCG,
∵AE∥CF,
∴∠EAD=∠CFD,
∴△ADE∽△FCD,
∴=,
∴CF DE=AD CD,
∵AE=CF=DE,
∴AE2=AD DC.
11.如图,在矩形ABCD中,AB=3,BC=5,BE平分∠ABC交AD于点E.连接CE,点F是BE上一动点,过点F作FG∥CE交BC于点G.将△BFG绕点B旋转得到△BF'G'.
(1)连接CG',EF',求证:△BEF'∽△BCG';
(2)当点G'恰好落在直线AE上时,若BF=3,求EG'的值.
【分析】(1)可证得∠F′BE=∠CBG′,=,从而证明了结论;
(2)先求得BG的长,进而求得BG′,然后解直角三角形ABG′求得结果.
【解答】(1)证明:∵FG∥CE,
∴△BFG∽△BEC,
∴=,
∴=,
∵∠F′BG′=∠EBC,
∴∠FBG′+∠EBG′=∠EBC+∠EBG′,
即∠F′BE=∠CBG,
∴△BEF′∽△BCG′;
(2)如图1,
∵四边形ABCD是矩形,
∴∠D=∠A=∠ABC=90°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=45°,
∴∠AEB=90°﹣∠ABE=45°,
∴∠AEB=∠ABE,
∴AE=AB=3,
∴BE=3,
由(1)知:=,
∴=,
∴BG=,
∴BG′=BG=,
在Rt△ABG′中,由勾股定理得,
AG′===,
∴EG′=AE﹣AG′=3﹣=,
EG″=,
综上所述:EG′=.
12.如图,正方形ABCD,E、F分别是边AB,BC的中点,AF与DE,DB分别交于点M,N.
(1)求证:AF=DE,AF⊥DE.
(2)求AM:MN:NF的值.
【分析】(1)根据SAS证明△ADE≌△BAF,即可得AF=DE,∠ADE=∠BAF,故∠ADE+∠AED=∠BAF+∠AED=90°,AF⊥DE;
(2)设正方形ABCD的边长为2x,则AE=BF=x,由勾股定理和面积法可得AM==x,证明△NAD∽△NFB,可得NF=AF=x,即可得到答案.
【解答】(1)证明:∵正方形ABCD,
∴AB=DA,∠ABC=∠BAD=90°,
∵E、F为边AB、BC的中点,
∴BF=AE,
在△ADE与△BAF中,
,
∴△ADE≌△BAF(SAS),
∴AF=DE,∠ADE=∠BAF,
∴∠ADE+∠AED=∠BAF+∠AED=90°,
∴∠AME=90°,
∴AF⊥DE;
(2)解:设正方形ABCD的边长为2x,则AE=BF=x,
在Rt△ADE中,DE==x,
由(1)知DE=AF,
∴AF=x,
∵2S△ADE=AE AD=DE AM,
∴AM==x,
∵AD∥BC,
∴∠ADN=∠NBF,∠NAD=∠NFB,
∴△NAD∽△NFB,
∴==2,
∴AN=2FN,
∴NF=AF=x,
∴MN=AF﹣AM﹣NF=,
∴AM:MN:NF=x:x:x=6:4:5.
13.问题背景
如图1,在△ABC中,点D,E分别在AC,AB上,2∠EDB+∠BDC=180°,∠DEB=90°,求证:AE=BE.
变式迁移
如图2,在四边形DEBC中,2∠EDB+∠BDC=180°,∠DEB=90°,DF∥EB,DF分别交CE,BC于点G,F,求证:DG=FG.
拓展应用
如图3,在四边形DECB中,2∠DBE+∠EBC=180°,∠EDB=∠DCB,,且n>1,直接写出的值.
【分析】问题背景:由2∠EDB+∠BDC=180°,∠ADB+∠BDC=180°,得出∠ADE=∠EDB,由∠DEB=90°,得出∠DEA=∠DEB=90°,即可得出△DEA≌△DEB,进而证明AE=BE;
变式迁移:延长CD,BE交于点M,则ME=BE,由DF∥BE,得出△CDG∽△CME,△CFG∽△CBE,进而得出,即可证明DG=FG;
拓展应用:在CB的延长线上截取BP=BE,连接DP,由“问题背景”可知:∠DBP=∠DBE,进而得出△DBE≌△DBP,得出∠EDB=∠PDB,由∠EDB=∠DCB,得出∠PDB=∠DCB,继而证明△DPB∽△CPD,得出===,设BP=1,则PD=n,得出PC=n2,求出BC=n2﹣1,继而得出=n2﹣1.
【解答】问题背景:证明:如图1,
∵2∠EDB+∠BDC=180°,∠ADB+∠BDC=180°,
∴∠ADB=2∠EDB,
∴∠ADE+∠EDB=2∠EDB,
∴∠ADE=∠EDB,
∵∠DEB=90°,
∴∠DEA=∠DEB=90°,
在△DEA和△DEB中,
,
∴△DEA≌△DEB(ASA),
∴AE=BE;
变式迁移:证明:如图2,延长CD,BE交于点M,则ME=BE,
∵DF∥BE,
∴∠CDG=∠M,∠CGD=∠CEM,∠CGF=∠CEB,∠CFG=∠CBE,
∴△CDG∽△CME,△CFG∽△CBE,
∴,,
∴,
∵ME=BE,
∴DG=FG;
拓展应用:解:如图3,在CB的延长线上截取BP=BE,连接DP,
由“问题背景”可知:∠DBP=∠DBE,
在△DBE和△DBP中,
,
∴△DBE≌△DBP(SAS),
∴∠EDB=∠PDB,
∵∠EDB=∠DCB,
∴∠PDB=∠DCB,
∵∠P=∠P,
∴△DPB∽△CPD,
∴==,
∵,
∴===,
设BP=1,则PD=n,
∴,
∴PC=n2,
∴BC=PC﹣BP=n2﹣1,
∴===n2﹣1.
14.问题提出
(1)如图①正三角形ABC,边长为4,D、E是边AB、AC的中点,P在BC边上,则△PDE的面积为 2 ;
问题解决
(2)如图②,某小区有一块五边形空地ABCDE,CD⊥DE,AE∥CD,CB=CD=40m,AE=10米,∠ABC=∠BCD=120°,物业想在这块空地中划出一块△MNP区域来种植草皮,其他区域种植花卉.已知种植花卉每平方米200元,种植草皮每平方米100元.要求M,N,P分别位于AB,ED,CD边上,且MN∥CD,要使种植费用的造价最低,种植草皮的△MNP的面积应该满足什么条件?并求出费用的最小值.
【分析】(1)过点A作AH⊥BC于H,根据三角函数求出AH,由中位线定理得出DE的长度,再根据三角形面积公式求出面积即可;
(2)延长AB交DC延长线于点G,要使种植费用最低,则种植草皮的面积最大,即△MNP面积最大,作MF⊥DC于点F,设QH=m,用m的代数式表示出△MNP的面积,利用二次函数的性质求最值即可.
【解答】解:(1)过点A作AH⊥BC于H,
∵△ABC是等边三角形,D、E是边AB、AC的中点,
∴DE∥BC,DE=BC=2,
∵AH=tan∠ABC AB=4,
∴△PDE的高为AH=2,
∴△PDE的面积为×2×2=2,
故答案为:2;
(2))延长AB交DC延长线于点G,
要使种植费用最低,则种植草皮的面积最大,即△MNP面积最大,
作MF⊥DC于点F,
∵∠ABC=∠BCD=120°,
∴∠GBC=∠BCG=60°,
∴△GBC为等边三角形,
即GC=BC=40m,GD=GC+CD=80m,
作MF⊥CD于F,设GF=x,
则MF=GF tan60°=x,
∵MN∥CD,MF⊥CD,ND⊥CD,
∴四边形MNDF是矩形,
∴MN=FD=GD﹣GF=80﹣m,
∴S△MNP=(80﹣m)×m=﹣(m﹣40)2+800,
∵﹣<0,
∴当m=40时,△MNP的面积最大为800,
作AQ⊥MN于Q,则MQ=MN﹣NQ=MN﹣AE=80﹣40﹣10=30,
∴AQ=MQ tan60°=30,
此时花卉种植面积为S梯形AEDG﹣S△BCG﹣S△MNP=(10+80)×(30+40)﹣×40×20﹣800=1950,
∴总费用为800×100+1950×200=470000(元),
即要使种植费用的造价最低,种植草皮的△MNP的面积最大,费用的最小值为470000元.
15.如图,在正方形ABCD中,点E在BC边上,连接AE,在BC延长线上作EF=AE,连接AF交CD于点G,设CE:EB=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若G点为CD的中点,①求证:EG⊥AF.②求λ的值.
【分析】(1)根据AB=2,λ=1,可以得到BE、CE的长,然后根据正方形的性质,可以得到AE的长,再根据平行线的性质和角平分线的性质,可以得到EF的长,从而可以得到线段CF的长;
(2)①要证明点G为CD边的中点,只要证明△ADG≌△FGC即可,然后根据题目中的条件,可以得到△ADG≌△FGC的条件,从而可以证明结论成立;
②根据题意和三角形相似,可以得到CE和EB的比值,从而可以得到λ的值.
【解答】解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE==,
∴EF=,
∴CF=EF﹣EC=﹣1;
(2)①证明:∵EA=EF,点G为CD的中点,
∴DG=CG,
在△ADG和△FCG中
,
∴△ADG≌△FCG(AAS),
∴AG=FG,
∵AE=EF,
∴EG⊥AF;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GCF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴△EGC∽△GFC,
∴=,
∵GC=a,FC=2a,
∴=,
∴=,
∴EC=a,BE=BC﹣EC=2a﹣a=a,
∴λ===.
16.如图,已知△ABC,点D,E分别在BC,CA上,且满足AD=AB,EB=EC.
(1)用直尺和圆规确定点D,E;(保留作图痕迹,不写作法)
(2)连接AD,EB,AD与EB交于点F.
①求证:△BDF∽△CBA;
②若∠BAC=90°,AB=3,AC=4,则DF的长为 .
【分析】(1)以A点为圆心AB长为半径画弧交BC于点D,作BC的垂直平分线交AC于E即可;
(2)①根据等腰三角形的性质得出两组对应角相等即可证明三角形相似;
②过点A作AH⊥BD于点H,根据勾股定理求出BC的长度,刘勇三角函数求出BH,根据等腰三角形的性质得出BD,再根据相似三角形对应边成比例求出DF即可.
【解答】解:(1)作图如下:
(2)①如下图:
∵AB=AD,
∴∠ABD=∠ADB,
∵EB=EC,
∴∠EBD=∠C,
∴△BDF∽△CBA;
②过点A作AH⊥BD于点H,
∵∠BAC=90°,AB=3,AC=4,
∴BC===5,
∵cos∠ABH=,
∴=,
∴BH=,
∵AB=AD,
∴BD=2BH=,
由①知△BDF∽△CBA,
∴,
即,
解得DF=,
故答案为:.
17.如图,△ABC是等腰直角三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,DE⊥DF,∠DEF=45°,DF的延长线与BC的延长线相交于点G.
(1)求证:△BDE∽△CEF;
(2)若AD=1,AF=2,求EC的长;
(3)若,求的值.
【分析】(1)根据已知可得∠B=∠C=45°,再根据∠DEF=45°,然后利用一线三等角模型证明,即可解答;
(2)过点E作EH⊥AB,垂足为H,根据已知可得DE=DF,然后证明一线三等角模型全等△ADF≌△HED,从而可得AD=EH=1,AF=DH=2,进而可求出BH,BE,AB,BC的长,进行计算即可解答;
(3)过点C作MC⊥AC,交DG于点M,可得AB∥CM,根据已知在Rt△DHE中,设EH=m,则DH=2m,利用(2)的结论可得EH=AD=BH=m,DH=AF=2m,BE=BH=m,从而求出BE,BC,CF的长,进而可得AF=CF,然后证明△ADF≌△CMF,利用全等三角形的性质可得AD=CM=m,最后证明△BDG∽△CMG,利用相似三角形的性质进行计算可求出CG的长,从而求出EG的长,即可解答.
【解答】(1)证明:∵AB=AC,∠A=90°,
∴∠B=∠C=45°,
∴∠BDE+∠BED=180°﹣∠B=135°,
∵∠DEF=45°,
∴∠BED+∠FEG=180°﹣∠DEF=135°,
∴∠BDE=∠FEG,
∴△BDE∽△CEF;
(2)过点E作EH⊥AB,垂足为H,
∵DE⊥DF,
∴∠EDF=90°,
∵∠DEF=45°,
∴DE=DF,
∵∠ADF+∠EDB=90°,∠ADF+∠AFD=90°,
∴∠AFD=∠EDB,
∵∠A=∠EHD=90°,
∴△ADF≌△HED(AAS),
∴AD=EH=1,AF=DH=2,
∵∠BHE=90°,∠B=45°,
∴BH=HE=1,
∴BE=BH=,AB=AD+DH+BH=4,
∵BC=AB=4,
∴EC=BC﹣BE=3;
(3)过点C作MC⊥AC,交DG于点M,
∴∠A=∠MCA=90°,
∴CM∥AB,
在Rt△DHE中,,
∴=,
设EH=m,则DH=2m,
由(2)得:EH=AD=BH=m,DH=AF=2m,BE=BH=m,
∴AC=AB=AD+DH+BH=4m,
∴BC=AB=4m,CF=AC﹣AF=4m﹣2m=2m,
∴AF=CF,
∵∠A=∠MCF=90°,∠AFD=∠MFC,
∴△ADF≌△CMF(ASA),
∴AD=CM=m,
∵CM∥AB,
∴∠B=∠MCG,∠BDG=∠CMG,
∴△BDG∽△CMG,
∴=,
∴=,
∴CG=2m,
∴EG=BC+CG﹣BE=5m,
∴==5,
∴的值为5.
18.如图,在正方形ABCD中,点E是边AD上的一点(不与A、D重合),点F在边DC延长线上,CF=AE,连接BE、BF、EF,EF交BC于点M,交对角线BD于N.
(1)求证:∠BEF=45°;
(2)若BE平分∠ABD,求证:BE2=AB BM;
(3)若DE:EA=3:2,则EN:NM:MF= 21:29:20 (直接写答案).
【分析】(1)先证明△ABD≌△BCF,进而便可得∠BEF的度数;
(2)证明BD=AB,再证明△EBD∽△MBF,得BE BF=BD MB,进而便可得出结论;
(3)设正方形ABCD的边长为a,用a表示AE、CF、DE,证明△FMC∽△MED,用a表示CM,进而用a表示BM,再证明△EDN∽△MBN,便可求得EN:MN,进而便可求得结果.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°=∠BCF,
∵AE=CF,
∴△ABD≌△BCF(SAS),
∴BE=BF,∠ABE=∠CBF,
∴∠ABF=∠EBC+CBF=∠EBC+∠ABE=∠ABC=90°,
∴∠BEF=∠BFE=45°;
(2)证明:由(1)知,∠BFE=∠BEF=45°,BE=BF,
∵四边形ABCD是正方形,
∴∠EDB=∠ABD=45°,∠ABC=90°,
∴BD=AB,
∵BE平分∠ABD,
∴∠ABE=∠EBD,
∴∠CBF=90°﹣∠EBC=∠ABE=∠EBD,
∵∠EDB=∠NFB=45°,
∴△EBD∽△MBF,
∴,
∴BE BF=BD MB,
∵BE=BF,BD=AB,
∴;
(3)解:设正方形ABCD的边长为a,
∵DE:EA=3:2,
∴AE=AD=,DE=a,
∴CF=AE==,
∵CD=AD=a,
∴CF:DF=2:7,
∵CM∥DE,
∴△FMC∽△FED,
∴=,
∴CM=DE=,
∴BM=BC﹣CM=a﹣=a,
∵DE∥BM,
∴△EDN∽△MBN,
∴,
设EN=21k,则MN=29k,
∵,
∴MF=,
∴MF=20k,
∴EN:NM:MF=21k:29k:20k=21:29:20.
故答案为:21:29:20.
19.如图1,在四边形ABCD中,∠ABC=∠BCD,过点A作AE∥DC交BC边于点E,过点E作EF∥AB交CD边于点F,连接AF,过点C作CH∥AF交AE于点H,连接BH.
(1)求证:△ABH≌△EAF;
(2)如图2,若BH的延长线经过AF的中点M,求的值.
【分析】(1)由∠ABC=∠BCD和AE∥DC可得AB=AE,由EF∥AB可得∠BAH=∠AEF,由AE∥DC,CH∥AF可得四边形AHCF为平行四边形,从而可得AH=CF,再由EF∥AB可得∠ABC=∠CEF,从而可得EF=CF,即可得出EF=AH,即可证明;
(2)延长BM,EF交于点G,由EF∥AB可得∠ABE=∠FEC,由AE∥CF可得∠AEB=∠FCE,从而可得△ABE∽△FEC,设EF=CF=a,AB=AE=ax,由点M为AF中点可得AM=FM,由EF∥AB可得∠ABM=∠FGM,可证△ABM≌△FGM(AAS),则FG=AB=ax,则EG=EF+FG=a+ax,由(1)可知四边形AHCF为平行四边形,可得AH=CF=a,则EH=AE﹣AH=ax﹣a,由AB∥EG可得△ABH∽△EGH,从而可得=,即=,解得x=1±,由x>0可得x=1+,即=x=1+.
【解答】(1)证明:∵AE∥DC,
∵∠AEB=∠BCD,
∵∠ABC=∠BCD,
∴∠AEB=∠ABC,
∴AB=AE,
∵EF∥AB,
∴∠BAH=∠AEF,
∵AE∥DC,CH∥AF,
∴四边形AHCF为平行四边形,
∴AH=CF,
∵EF∥AB,
∴∠ABC=∠CEF,
∵AE∥CF,
∴∠ECF=∠AEB=∠ABC,
∴∠ECF=∠CEF,
∴EF=CF,
∴EF=AH,
∴△ABH≌△EAF(SAS);
(2)如图,延长BM,EF交于点G,
∵EF∥AB,
∴∠ABE=∠FEC,
∵AE∥CF,
∴∠AEB=∠FCE,
∴△ABE∽△FEC,
设EF=CF=a,AB=AE=ax,
∵点M为AF中点
∴AM=FM,
∵EF∥AB
∴∠ABM=∠FGM,
∴△ABM≌△FGM(AAS),
FG=AB=ax,
∴EG=EF+FG=a+ax,
由(1)可知四边形AHCF为平行四边形,
∴AH=CF=a,
∴EH=AE﹣AH=ax﹣a,
∵AB∥EG
∴△ABH∽△EGH,
∴=,
即=,
解得x=1±,
∵x>0,
∴x=1+,
即=x=1+.
20.如图1,在矩形ABCD中,AB=5,AD=8,点E在边CD上,tan∠BAE=2,点F是线改AE上一点,连接CF.
(1)连接BF,请用尺规作图法作FG⊥AB,垂足为G点(保留作图痕迹,不要求写出作法).若tan∠ABF=,求线段AF的长.
(2)如图2,若CF=BC,AE的延长线与BC的延长线交于点H,求△CEF的面积.
【分析】(1)根据垂线的画法画图即可;设AG=x,则BG=5﹣x,在Rt△AFG中,tan∠BAE==2,可得FG=2x,在Rt△BFG中,tan∠ABF=,求得x=2,由勾股定理可得AF=,即可得出答案.
(2)过点C作CM⊥AH于点M,在Rt△ABH中,tan∠BAE==2,可得BH=10,CH=BH﹣BC=2,根据AB∥CD,可得∠CEH=∠BAE,则tan∠CEH==2,可得CE=1,在Rt△CEM中,tan∠CEM==2,设EM=a,则CM=2a,由勾股定理可得CE2=EM2+CM2,即可求得a=,则CM=,在Rt△CFM中,CF=BC=2,由勾股定理可得FM==,进而可得EF=FM﹣EM=,则根据EF CM可得出答案.
【解答】解:(1)如图,FG即为所求.
设AG=x,则BG=5﹣x,
在Rt△AFG中,
tan∠BAE==2,
∴FG=2x,
在Rt△BFG中,
tan∠ABF=,
解得x=2,
∴AG=2,FG=4,
AF==2.
(2)过点C作CM⊥AH于点M,
在Rt△ABH中,
tan∠BAE==2,
∴BH=10,
则CH=BH﹣BC=2,
∵四边形ABCD为矩形,
∴AB∥CD,
∴∠CEH=∠BAE,
则tan∠CEH==2,
∴CE=1,
在Rt△CEM中,tan∠CEM==2,
设EM=a,则CM=2a,
由勾股定理可得CE2=EM2+CM2,
即a2+(2a)2=12,
解得a=,
∴CM=,
在Rt△CFM中,CF=BC=2,
由勾股定理可得FM==,
∴EF=FM﹣EM=.
∴EF CM=.
同课章节目录
