人教版八年级数学上册 11.3.2多边形内角和 导学案(表格式,无答案)
文档属性
| 名称 | 人教版八年级数学上册 11.3.2多边形内角和 导学案(表格式,无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 170.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 17:59:15 | ||
图片预览


文档简介
八年级数学上册导学案
日期 主备教师 课型
课题 11.3.2 多边形的内角和
学习目标 ①掌握多边形的内角和的计算方法, ②能用内角和知识解决一些较简单的问题; ③通过多边形内角和的计算公式的推导,培养探索和归纳的能力
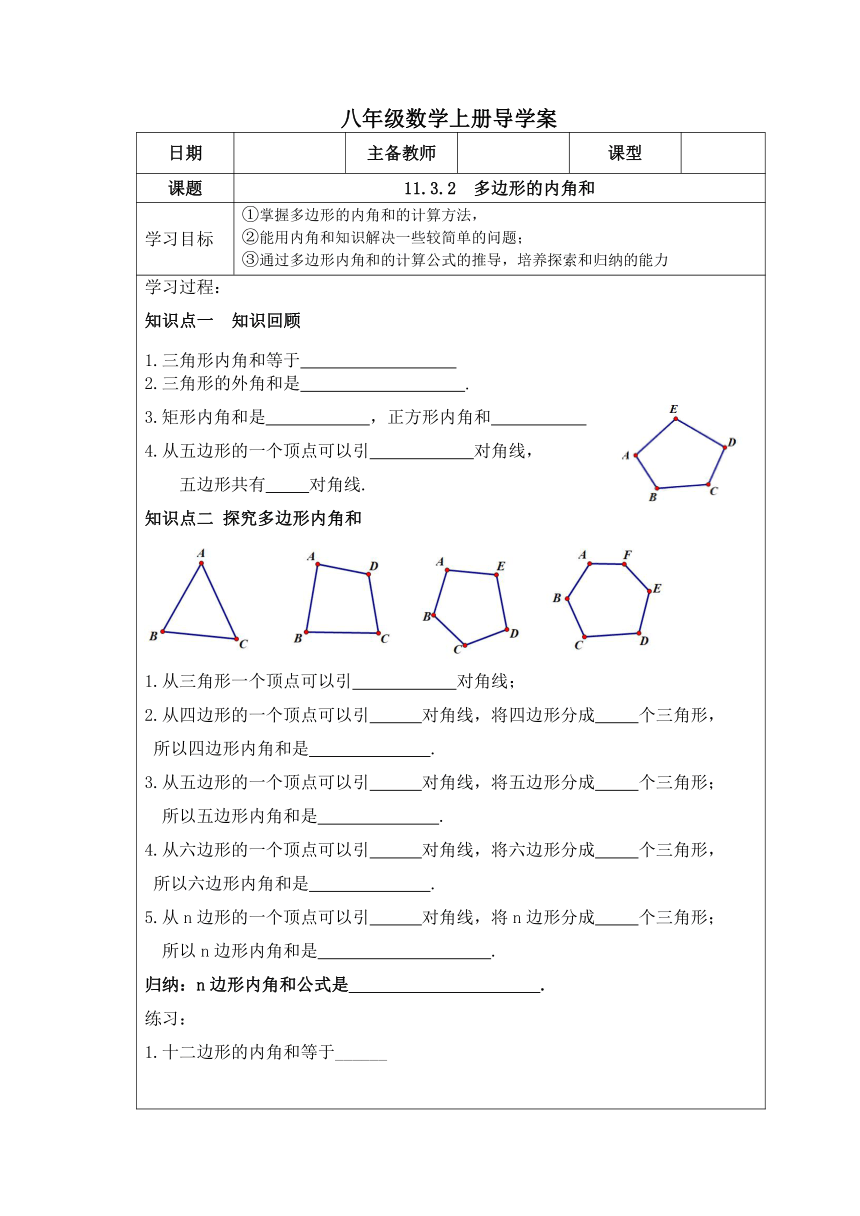
学习过程: 知识点一 知识回顾 1.三角形内角和等于 2.三角形的外角和是 . 3.矩形内角和是 ,正方形内角和 4.从五边形的一个顶点可以引 对角线, 五边形共有 对角线. 知识点二 探究多边形内角和 1.从三角形一个顶点可以引 对角线; 2.从四边形的一个顶点可以引 对角线,将四边形分成 个三角形, 所以四边形内角和是 . 3.从五边形的一个顶点可以引 对角线,将五边形分成 个三角形; 所以五边形内角和是 . 4.从六边形的一个顶点可以引 对角线,将六边形分成 个三角形, 所以六边形内角和是 . 5.从n边形的一个顶点可以引 对角线,将n边形分成 个三角形; 所以n边形内角和是 . 归纳:n边形内角和公式是 . 练习: 1.十二边形的内角和等于______
2. 已知一个多边形的内角和等于2340°,它的边数是 . 例题分析: 例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由. 1.判断.
(1)当多边形边数增加时,它的内角和也随着增加. ( )
(2)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-1)个 三角形. ( ) 一般四边形内角和与矩形的内角和不相等( ) 十边形内角和是18000( ) 知识点三 探究多边形外角和 1.n边形的外角和:在n边形每个顶点上取 个外角,n个外角的 , 叫n边形的外角和 2.三角形外角和是 ;矩形外角和是 ,正方形外角和是 . 3.佳佳沿一个五边形广场周围的小跑,按逆时针方向跑步. (1)佳佳每从一条小路转到下一条小路时,跑步方向改变的哪个角?在图中标出. (2)他每跑完一圈,身体转过的角度之和是多少?说明理由. 结论:五边形外角和是 . n边形外角和是 . 例题分析2: 一个多边形的内角和等于它的外角和的3 倍,它是几边形?
跟踪练习: 判断 (1)当多边形边数增加时,它的外角和也随着增加. ( ) (2)三角形的外角和与八边形的外角和相等. ( ) 2.一个多边形内角和与一个外角的和是2380°,则这个多边形的边数为 . 3.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD. 求∠P的度数。 当堂检测: 1.求出下列图形中x的值。 五边形的内角和为 ,它的对角线有 条. 如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______. 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( ) A.360° B.540° C.720° D.900° 一个正多边形的外角与它相邻的内角之比为1∶4,那么这个多边形的边数为( ) A.8 B.9 C.10 D.12 6.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540 ° C.720 ° D.900 ° 7.已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
日期 主备教师 课型
课题 11.3.2 多边形的内角和
学习目标 ①掌握多边形的内角和的计算方法, ②能用内角和知识解决一些较简单的问题; ③通过多边形内角和的计算公式的推导,培养探索和归纳的能力
学习过程: 知识点一 知识回顾 1.三角形内角和等于 2.三角形的外角和是 . 3.矩形内角和是 ,正方形内角和 4.从五边形的一个顶点可以引 对角线, 五边形共有 对角线. 知识点二 探究多边形内角和 1.从三角形一个顶点可以引 对角线; 2.从四边形的一个顶点可以引 对角线,将四边形分成 个三角形, 所以四边形内角和是 . 3.从五边形的一个顶点可以引 对角线,将五边形分成 个三角形; 所以五边形内角和是 . 4.从六边形的一个顶点可以引 对角线,将六边形分成 个三角形, 所以六边形内角和是 . 5.从n边形的一个顶点可以引 对角线,将n边形分成 个三角形; 所以n边形内角和是 . 归纳:n边形内角和公式是 . 练习: 1.十二边形的内角和等于______
2. 已知一个多边形的内角和等于2340°,它的边数是 . 例题分析: 例1.如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由. 1.判断.
(1)当多边形边数增加时,它的内角和也随着增加. ( )
(2)从n边形一个顶点出发,可以引出(n-2)条对角线,得到(n-1)个 三角形. ( ) 一般四边形内角和与矩形的内角和不相等( ) 十边形内角和是18000( ) 知识点三 探究多边形外角和 1.n边形的外角和:在n边形每个顶点上取 个外角,n个外角的 , 叫n边形的外角和 2.三角形外角和是 ;矩形外角和是 ,正方形外角和是 . 3.佳佳沿一个五边形广场周围的小跑,按逆时针方向跑步. (1)佳佳每从一条小路转到下一条小路时,跑步方向改变的哪个角?在图中标出. (2)他每跑完一圈,身体转过的角度之和是多少?说明理由. 结论:五边形外角和是 . n边形外角和是 . 例题分析2: 一个多边形的内角和等于它的外角和的3 倍,它是几边形?
跟踪练习: 判断 (1)当多边形边数增加时,它的外角和也随着增加. ( ) (2)三角形的外角和与八边形的外角和相等. ( ) 2.一个多边形内角和与一个外角的和是2380°,则这个多边形的边数为 . 3.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD. 求∠P的度数。 当堂检测: 1.求出下列图形中x的值。 五边形的内角和为 ,它的对角线有 条. 如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______. 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( ) A.360° B.540° C.720° D.900° 一个正多边形的外角与它相邻的内角之比为1∶4,那么这个多边形的边数为( ) A.8 B.9 C.10 D.12 6.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540 ° C.720 ° D.900 ° 7.已知一个多边形的每个内角与外角的比都是7:2,求这个多边形的边数.
