沪科版七年级数学上册1.4有理数的加法运算 同步练习 (word版含答案)
文档属性
| 名称 | 沪科版七年级数学上册1.4有理数的加法运算 同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 20:03:34 | ||
图片预览




文档简介
1.4有理数的加法运算
一、单选题
1.下列运算中,正确的是( )
A.﹣4﹣2=﹣2 B.3﹣(﹣3)=0
C.10+(﹣8)=﹣2 D.﹣5﹣4﹣(﹣4)=﹣5
2.下列说法中,正确的个数有( )
①是正数;
②绝对值最小的数是0;
③一个有理数的绝对值是它本身,则这个数是正数;
④如果两个数的和为正数,那么这两个数中至少有一个正数.
A.0个 B.1个 C.2个 D.3个
3.下列说法正确的是( )
A.两个有理数相加和一定大于每个加数 B.两个非零有理数相加,和可能等于零
C.两个有理数和为负数时,这两个数都是负数 D.两个负数相加,把绝对值相加
4.绝对值大于而不大于的所有整数的和等于( )
A.12 B.0 C.-12 D.-13
5.下列式子不可读作“负1,负3,正6,负8”的和的是( )
A. B.
C. D.
6.若a+b<0,a>0,b<0,则a,-a,b,-b的大小关系是( )
A.b<-a7.实数a在数轴上的对应点的位置如图所示,若实数b满足,则b的值可以是( )
A.-2 B.-1 C.1 D.2
8.小戴同学的微信钱包账单如图所示, 表示收入 元,下列说法正确的是( )
A. 表示收入 元 B. 表示支出 元
C. 表示支出 元 D.收支总和为 元
9.某个地区,一天早晨的温度是,中午上升了,则中午的温度是( )
A. B. C. D.
10.某市客运管理部门对“五一”黄金周假期五天的客流变化量做了不完全统计,数据如下(用正数表示客流量比前一天上升数,用负数表示下降数):
日期 1日 2日 3日 4日 5日
变化/万人 20 ﹣2 ﹣5 9 3
与4月30日比,5月3日的客流量变化了多少( )
A.下降了5万人 B.上升了13万人
C.上升了21万人 D.下降了7万人
二、填空题
11.有理数的加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和_____.
12.有理数的加法交换律:两个数相加,交换加数的位置,和______________.
13.计算_______.可以运用_______律作简便运算.
14.若a+b+c=0且a>b>c,则下列几个数中:①a+b;②ab;③ab2;④b2﹣ac;⑤﹣(b+c),一定是正数的有 _______(填序号).
15.若a>0,b<0,|a|>|b|,则a+b_____0(用“>”或“<”填空).
三、解答题
16.计算:
(1)(-0.9)+(-2.7); (2)3.8+(-8.4);
(3)(-0.5)+3; (4)3.92+1.78;
(5)7+(-3.04); (6)(-2.9)+(-0.31);
(7)(-9.18)+6.18; (8)4.23+(-6.77).
17.计算:
(1); (2);
.
18.已知|x|=3,|y|=2.
(1)若x>0,y<0,求x+y的值;
(2)若x<y,求x﹣y的值.
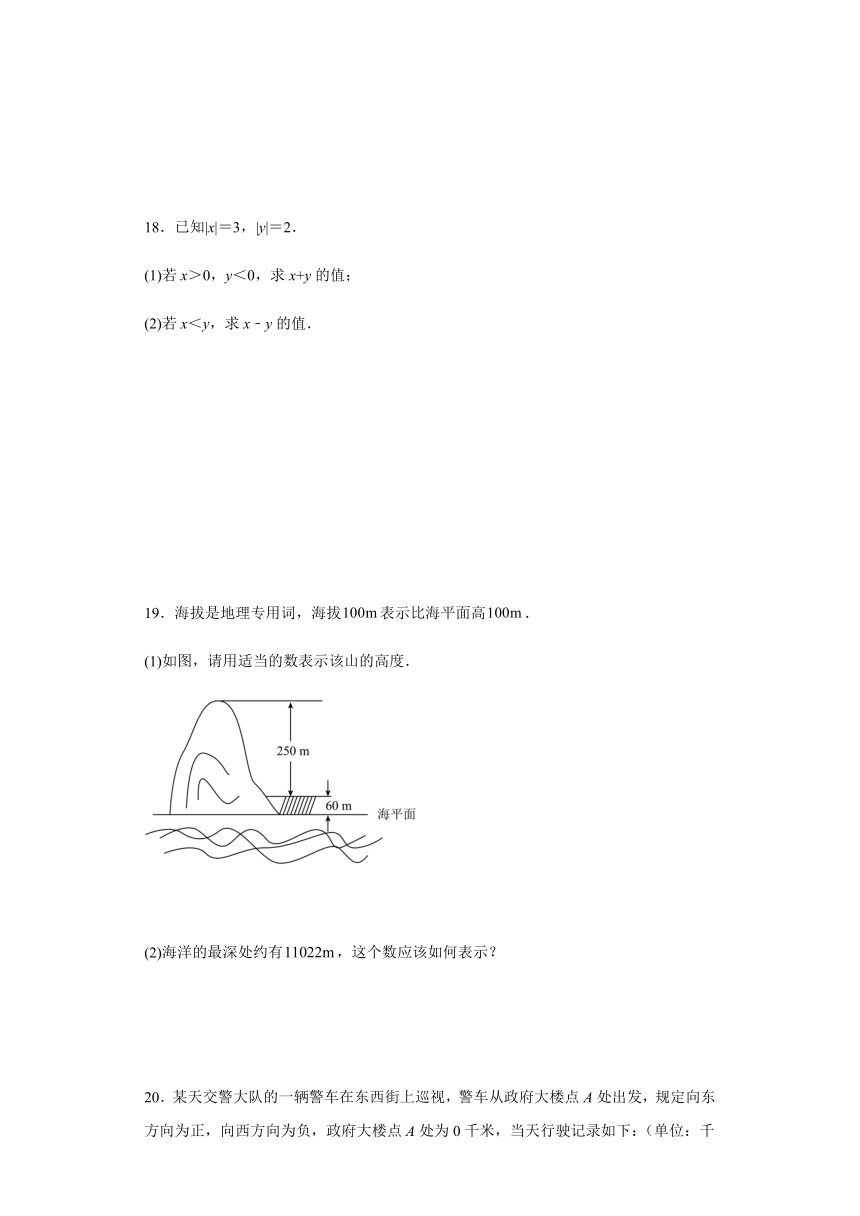
19.海拔是地理专用词,海拔表示比海平面高.
(1)如图,请用适当的数表示该山的高度.
海洋的最深处约有,这个数应该如何表示?
20.某天交警大队的一辆警车在东西街上巡视,警车从政府大楼点A处出发,规定向东方向为正,向西方向为负,政府大楼点A处为0千米,当天行驶记录如下:(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2.
(1)第8次行驶结束时,警车是否回到政府大楼点A处 若没有,在政府大楼点A处何方 距离政府大楼点A多远
(2)警车当天共行驶了多少千米
21.一名快递员从快递公司出发负责在东西方向的路上送快递,向东走了4千米到达小明家,继续走了1千米到达小红家,从小红家调头向西走了10千米到达小刚家,最后回到快递公司.
(1)以快递公司为原点,向东的方向为正方向,用1个单位长度表示1千米,请你画出数轴,并在数轴上分别表示出小明家、小红家、小刚家的位置.
(2)小明家和小刚家相距多远?
(3)快递员从出发到最后回到快递公司一共走了多少千米?
简要参考答案:
1.D
2.C
3.B
4.B
5.B
6.A
7.D
8.B
9.C
10.B
11.不变
12.不变
13. 加法交换、结合律
14.①④⑤
15.>
16.(1)-3.6
(2)-4.6
(3)2.5
(4)5.7
(5)3.96
(6)-3.21
(7)-3
(8)-2.54
17.(1)﹣2
(2)0
(3)0
18.(1)1
(2)﹣5或﹣1
19.(1)该山的高度为310米
(2)这个数应该表示为
20.(1)没有回到政府大楼点A处,在政府大楼西边4千米处
(2)58千米
21.(1)见解析
(2)小明家和小刚家相距9千米
(3)快递员从出发到最后回到快递公司一共走了20千米.
详细参考答案:
1.D
【详解】解:A、﹣4﹣2=﹣6,故本选项错误,不符合题意;
B、3﹣(﹣3)=6,故本选项错误,不符合题意;
C、10+(﹣8)=2,故本选项错误,不符合题意;
D、﹣5﹣4﹣(﹣4)=﹣5,故本选项正确,符合题意;
故选:D
2.C
【详解】解:①当时,,不是正数,说法错误;
②绝对值最小的数是0,说法正确;
③一个有理数的绝对值是它本身,则这个数是正数或者0,说法错误;
④如果两个数的和为正数,那么这两个数中至少有一个正数,说法正确;
∴正确的一共有2个,
故选C.
3.B
【详解】解:A.不能确定,例如:(﹣1)+(﹣2)=﹣3,故A错误;
B.正确,互为相反数的两个数相加和为0,故B正确;
C.不能确定,例如:(﹣8)+2=﹣6,故C错误;
D.错误,两个负数相加,取原来的符号并把绝对值相加,故D错误.
故选:B.
4.B
【详解】解:绝对值大于而不大于的所有整数有:-3,-4,-5,3,4,5,
之和为0.
故选:B.
5.B
【详解】解:A、-1-3+6-8可读作“负1,负3,正6,负8”的和,故不符合题意;
B、=-1+(-3)+(-6)+(+8),不可读作“负1,负3,正6,负8”的和,故符合题意;
C、=-1+(-3)+(-6)+(-8),可读作“负1,负3,正6,负8”的和,故不符合题意;
D、=-1+(-3)+(-6)+(-8),可读作“负1,负3,正6,负8”的和,故不符合题意;
故选:B.
6.A
【详解】∵a>0,b<0,a+b<0,
∴|a|<|b|,
∴a,-a,b,-b的大小关系为:b<-a<a<-b.
故选:A.
7.D
【详解】解∶根据题意得∶,
∴,
∵,
∴,且,
∴,
∴b的值可以是2.
故选:D
8.B
【详解】解:∵+5.20表示收入5.20元,
∴-1.00表示支出1.00元,故B正确,A,C不正确;
收支总和为+5.20+(-1.00)=+4.20,收入4.20元,故D不正确;
故选:B.
9.C
【详解】解:∵早晨的温度是,中午上升了,
∴中午的温度是:,
故选:C
10.B
【详解】解:∵20﹣2﹣5=13(万人),
∴上升了13万人,
故选:B.
11.不变
【详解】解:有理数的加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
故答案为:不变.
12.不变
【详解】解:有理数的加法交换律:两个数相加,交换加数的位置,和不变.
故答案为:不变.
13. 加法交换、结合律
【详解】解:原式,
可以运用加法交换、结合律进行简算,
,
故答案为:;加法交换、结合律.
14.①④⑤
【详解】解:∵a+b+c=0且a>b>c,
∴a>0,c<0,b可以是正数,负数或0,
∴①a+b=-c>0,
②b=0时,ab=0,
③b=0时,=0,
④ac<0,b2﹣ac>0,
⑤-(b+c)=a>0.
故答案为:①④⑤.
15.>
【详解】∵a>0,b<0,|a|>|b|,
∴a>﹣b,
∴a+b>0.
故答案为:>.
16.(1)-3.6
(2)-4.6
(3)2.5
(4)5.7
(5)3.96
(6)-3.21
(7)-3
(8)-2.54
17.(1)﹣2
(2)0
(3)0
16.(1)
(1)
=(3+5)+[(﹣2)+(﹣8)]
=9﹣11
=﹣2;
(2)
(2)
=[(﹣0.5)+(﹣5)]+(3+2.75)
=﹣6+6
=0;
(3)
(3)
=﹣1.5++0
=0.
18.(1)1
(2)﹣5或﹣1
(1)
解:由|x|=3,|y|=2.x>0,y<0,得,x=3,y=﹣2,
∴x+y=3+(﹣2)=1;
所以x+y的值为1;
(2)
解:由|x|=3,|y|=2.x<y,可得x=﹣3,y=2或x=﹣3,y=﹣2,
当x=﹣3,y=2时,x﹣y=﹣3﹣2=﹣5,
或x=﹣3,y=﹣2时,x﹣y=﹣3﹣(﹣2)=﹣1,
所以x﹣y的值为﹣5或﹣1.
19.(1)该山的高度为310米
(2)这个数应该表示为
(1)
,
答:该山的高度为310米;
(2)
∵海拔表示比海平面高,
∴海洋的最深处约有,这个数应该表示为.
20.(1)没有回到政府大楼点A处,在政府大楼西边4千米处
(2)58千米
(1)
解:没有,
10-9+7-15+6-5+4-2=-4千米,
∴警车没有回到政府大楼点A处,在政府大楼西边4千米处;
(2)
10+9+7+15+6+5+4+2=58(千米),
∴当天共行驶了58千米.
21.(1)见解析
(2)小明家和小刚家相距9千米
(3)快递员从出发到最后回到快递公司一共走了20千米.
(1)
解:(1)如图所示:
(2)
解:由(1)数轴可知:小明家所在位置表示的数是4,小刚家所在位置表示的数是-5,
所以.
答:小明家和小刚家相距9千米.
(3)
解: 4+1+10+5=20.
答:快递员从出发到最后回到快递公司一共走了20千米.
一、单选题
1.下列运算中,正确的是( )
A.﹣4﹣2=﹣2 B.3﹣(﹣3)=0
C.10+(﹣8)=﹣2 D.﹣5﹣4﹣(﹣4)=﹣5
2.下列说法中,正确的个数有( )
①是正数;
②绝对值最小的数是0;
③一个有理数的绝对值是它本身,则这个数是正数;
④如果两个数的和为正数,那么这两个数中至少有一个正数.
A.0个 B.1个 C.2个 D.3个
3.下列说法正确的是( )
A.两个有理数相加和一定大于每个加数 B.两个非零有理数相加,和可能等于零
C.两个有理数和为负数时,这两个数都是负数 D.两个负数相加,把绝对值相加
4.绝对值大于而不大于的所有整数的和等于( )
A.12 B.0 C.-12 D.-13
5.下列式子不可读作“负1,负3,正6,负8”的和的是( )
A. B.
C. D.
6.若a+b<0,a>0,b<0,则a,-a,b,-b的大小关系是( )
A.b<-a
A.-2 B.-1 C.1 D.2
8.小戴同学的微信钱包账单如图所示, 表示收入 元,下列说法正确的是( )
A. 表示收入 元 B. 表示支出 元
C. 表示支出 元 D.收支总和为 元
9.某个地区,一天早晨的温度是,中午上升了,则中午的温度是( )
A. B. C. D.
10.某市客运管理部门对“五一”黄金周假期五天的客流变化量做了不完全统计,数据如下(用正数表示客流量比前一天上升数,用负数表示下降数):
日期 1日 2日 3日 4日 5日
变化/万人 20 ﹣2 ﹣5 9 3
与4月30日比,5月3日的客流量变化了多少( )
A.下降了5万人 B.上升了13万人
C.上升了21万人 D.下降了7万人
二、填空题
11.有理数的加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和_____.
12.有理数的加法交换律:两个数相加,交换加数的位置,和______________.
13.计算_______.可以运用_______律作简便运算.
14.若a+b+c=0且a>b>c,则下列几个数中:①a+b;②ab;③ab2;④b2﹣ac;⑤﹣(b+c),一定是正数的有 _______(填序号).
15.若a>0,b<0,|a|>|b|,则a+b_____0(用“>”或“<”填空).
三、解答题
16.计算:
(1)(-0.9)+(-2.7); (2)3.8+(-8.4);
(3)(-0.5)+3; (4)3.92+1.78;
(5)7+(-3.04); (6)(-2.9)+(-0.31);
(7)(-9.18)+6.18; (8)4.23+(-6.77).
17.计算:
(1); (2);
.
18.已知|x|=3,|y|=2.
(1)若x>0,y<0,求x+y的值;
(2)若x<y,求x﹣y的值.
19.海拔是地理专用词,海拔表示比海平面高.
(1)如图,请用适当的数表示该山的高度.
海洋的最深处约有,这个数应该如何表示?
20.某天交警大队的一辆警车在东西街上巡视,警车从政府大楼点A处出发,规定向东方向为正,向西方向为负,政府大楼点A处为0千米,当天行驶记录如下:(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2.
(1)第8次行驶结束时,警车是否回到政府大楼点A处 若没有,在政府大楼点A处何方 距离政府大楼点A多远
(2)警车当天共行驶了多少千米
21.一名快递员从快递公司出发负责在东西方向的路上送快递,向东走了4千米到达小明家,继续走了1千米到达小红家,从小红家调头向西走了10千米到达小刚家,最后回到快递公司.
(1)以快递公司为原点,向东的方向为正方向,用1个单位长度表示1千米,请你画出数轴,并在数轴上分别表示出小明家、小红家、小刚家的位置.
(2)小明家和小刚家相距多远?
(3)快递员从出发到最后回到快递公司一共走了多少千米?
简要参考答案:
1.D
2.C
3.B
4.B
5.B
6.A
7.D
8.B
9.C
10.B
11.不变
12.不变
13. 加法交换、结合律
14.①④⑤
15.>
16.(1)-3.6
(2)-4.6
(3)2.5
(4)5.7
(5)3.96
(6)-3.21
(7)-3
(8)-2.54
17.(1)﹣2
(2)0
(3)0
18.(1)1
(2)﹣5或﹣1
19.(1)该山的高度为310米
(2)这个数应该表示为
20.(1)没有回到政府大楼点A处,在政府大楼西边4千米处
(2)58千米
21.(1)见解析
(2)小明家和小刚家相距9千米
(3)快递员从出发到最后回到快递公司一共走了20千米.
详细参考答案:
1.D
【详解】解:A、﹣4﹣2=﹣6,故本选项错误,不符合题意;
B、3﹣(﹣3)=6,故本选项错误,不符合题意;
C、10+(﹣8)=2,故本选项错误,不符合题意;
D、﹣5﹣4﹣(﹣4)=﹣5,故本选项正确,符合题意;
故选:D
2.C
【详解】解:①当时,,不是正数,说法错误;
②绝对值最小的数是0,说法正确;
③一个有理数的绝对值是它本身,则这个数是正数或者0,说法错误;
④如果两个数的和为正数,那么这两个数中至少有一个正数,说法正确;
∴正确的一共有2个,
故选C.
3.B
【详解】解:A.不能确定,例如:(﹣1)+(﹣2)=﹣3,故A错误;
B.正确,互为相反数的两个数相加和为0,故B正确;
C.不能确定,例如:(﹣8)+2=﹣6,故C错误;
D.错误,两个负数相加,取原来的符号并把绝对值相加,故D错误.
故选:B.
4.B
【详解】解:绝对值大于而不大于的所有整数有:-3,-4,-5,3,4,5,
之和为0.
故选:B.
5.B
【详解】解:A、-1-3+6-8可读作“负1,负3,正6,负8”的和,故不符合题意;
B、=-1+(-3)+(-6)+(+8),不可读作“负1,负3,正6,负8”的和,故符合题意;
C、=-1+(-3)+(-6)+(-8),可读作“负1,负3,正6,负8”的和,故不符合题意;
D、=-1+(-3)+(-6)+(-8),可读作“负1,负3,正6,负8”的和,故不符合题意;
故选:B.
6.A
【详解】∵a>0,b<0,a+b<0,
∴|a|<|b|,
∴a,-a,b,-b的大小关系为:b<-a<a<-b.
故选:A.
7.D
【详解】解∶根据题意得∶,
∴,
∵,
∴,且,
∴,
∴b的值可以是2.
故选:D
8.B
【详解】解:∵+5.20表示收入5.20元,
∴-1.00表示支出1.00元,故B正确,A,C不正确;
收支总和为+5.20+(-1.00)=+4.20,收入4.20元,故D不正确;
故选:B.
9.C
【详解】解:∵早晨的温度是,中午上升了,
∴中午的温度是:,
故选:C
10.B
【详解】解:∵20﹣2﹣5=13(万人),
∴上升了13万人,
故选:B.
11.不变
【详解】解:有理数的加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
故答案为:不变.
12.不变
【详解】解:有理数的加法交换律:两个数相加,交换加数的位置,和不变.
故答案为:不变.
13. 加法交换、结合律
【详解】解:原式,
可以运用加法交换、结合律进行简算,
,
故答案为:;加法交换、结合律.
14.①④⑤
【详解】解:∵a+b+c=0且a>b>c,
∴a>0,c<0,b可以是正数,负数或0,
∴①a+b=-c>0,
②b=0时,ab=0,
③b=0时,=0,
④ac<0,b2﹣ac>0,
⑤-(b+c)=a>0.
故答案为:①④⑤.
15.>
【详解】∵a>0,b<0,|a|>|b|,
∴a>﹣b,
∴a+b>0.
故答案为:>.
16.(1)-3.6
(2)-4.6
(3)2.5
(4)5.7
(5)3.96
(6)-3.21
(7)-3
(8)-2.54
17.(1)﹣2
(2)0
(3)0
16.(1)
(1)
=(3+5)+[(﹣2)+(﹣8)]
=9﹣11
=﹣2;
(2)
(2)
=[(﹣0.5)+(﹣5)]+(3+2.75)
=﹣6+6
=0;
(3)
(3)
=﹣1.5++0
=0.
18.(1)1
(2)﹣5或﹣1
(1)
解:由|x|=3,|y|=2.x>0,y<0,得,x=3,y=﹣2,
∴x+y=3+(﹣2)=1;
所以x+y的值为1;
(2)
解:由|x|=3,|y|=2.x<y,可得x=﹣3,y=2或x=﹣3,y=﹣2,
当x=﹣3,y=2时,x﹣y=﹣3﹣2=﹣5,
或x=﹣3,y=﹣2时,x﹣y=﹣3﹣(﹣2)=﹣1,
所以x﹣y的值为﹣5或﹣1.
19.(1)该山的高度为310米
(2)这个数应该表示为
(1)
,
答:该山的高度为310米;
(2)
∵海拔表示比海平面高,
∴海洋的最深处约有,这个数应该表示为.
20.(1)没有回到政府大楼点A处,在政府大楼西边4千米处
(2)58千米
(1)
解:没有,
10-9+7-15+6-5+4-2=-4千米,
∴警车没有回到政府大楼点A处,在政府大楼西边4千米处;
(2)
10+9+7+15+6+5+4+2=58(千米),
∴当天共行驶了58千米.
21.(1)见解析
(2)小明家和小刚家相距9千米
(3)快递员从出发到最后回到快递公司一共走了20千米.
(1)
解:(1)如图所示:
(2)
解:由(1)数轴可知:小明家所在位置表示的数是4,小刚家所在位置表示的数是-5,
所以.
答:小明家和小刚家相距9千米.
(3)
解: 4+1+10+5=20.
答:快递员从出发到最后回到快递公司一共走了20千米.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
