2022-2023学年人教版数学九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 15.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 21:08:28 | ||
图片预览





文档简介
(共19张PPT)
22.1 二次函数的图像和性质
22.1.3 二次函数y=a(x-h) +k的图象和性质
九年级-上册-第二十二章
目录
CONTENTS
课前导入
二次函数的图像和性质
二次函数y=a(x-h) +k(a≠0)的图象和性质
课前导入二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
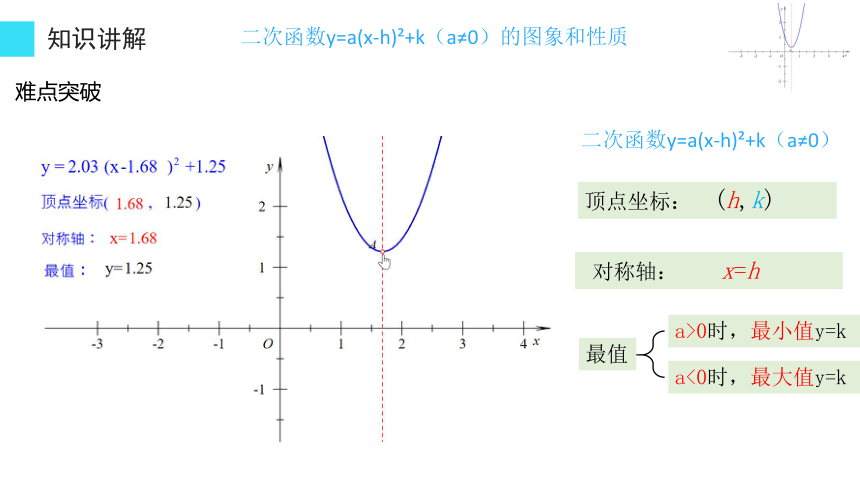
难点突破
开口方向
对称轴 x=h
顶点坐标 (h,k)
增减性
最值 y=k
(h,k)
x=h
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
开口方向
a>0,开口向上,并向上无限延伸
a<0,开口向下,并向下无限延伸
开口大小
|a|越大,开口越小
|a|越小,开口越大
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
对称轴: x=h
顶点坐标: (h,k)
最值
a>0时,最小值y=k
a<0时,最大值y=k
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
a>0
x>h时,即在对称轴的右侧,y随x的增大而增大
xa<0
x>h时,即在对称轴的右侧,y随x的增大而减小
x增减性
课堂练习
难点巩固
二次函数y=a(x-h) +k(a≠0)的图象和性质
对于抛物线y= -(x+1) +3,有以下结论: ①抛物线的开口向下; ②对称轴为直线x=1; ③顶点坐标为(-1,3); ④x>-1时,y随x的增大而减小;⑤最小值是3.其中正确的结论有 .
【课堂小结】
小结反思
二次函数y=a(x-h) +k(a≠0)的图象和性质
性质a 图像 开口方向 顶点坐标 对称轴 最值 增减性 对称轴左侧 对称轴右侧
a>0 向上 (h,k) x=h 最小值y=k y随x增大而减小
y随x增大而增大
a<0 向下 最大值y=k y随x增大而增大
y随x增大而减小
二次函数y=a(x-h) +k(a≠0)的图象和性质:
新疆教科研
微信公众号
22.1.3 二次函数y=a(x-h)2+k的图象和性质
(第2课时)
学习目标1.通过观察二次函数y=a(x-h)2+k(a≠0)的图象,得到抛物线的开口方向、对称轴和顶点坐标.2.理解抛物线y=a(x-h)2+k与y=ax2之间的关系.yxOyxOyxOyxOyxOyxOyxOyxOyxOyxO温故知新(1)y=ax2(2)y=ax2+k(3)y=a(x-h)2x=hx=hx=hx=h(0,k)(0,k)(0,k)(0,k)(h,0)(h,0)(h,0)(h,0)探究新知例3画出函数 的图像,并指出它的开口方向、对称轴和顶点.…………210-1-2-3-4x解:先列表-5.5-3-1.5-1-1.5-3-5.512345x-1-2-3-4-5-6-7-8-91yO-1-2-3-4-5-10然后描点画图,函数的图像如图所示.x=-1抛物线 的开口向下,对称轴是x=-1,顶点坐标是(-1,-1).(-1,-1)二次函数y=a(x-h)2+k的图象和性质12345x-1-2-3-4-5-6-7-8-91yO-1-2-3-4-5-10例3画出函数 的图像,并指出它的开口方向、对称轴和顶点.怎样移动抛物线 就可以得到抛物线 ?向左平移1个单位向下平移1个单位二次函数y=a(x-h)2+k的图象和性质探究新知12345x-1-2-3-4-5-6-7-8-91yO-1-2-3-4-5-10例3画出函数 的图像,并指出它的开口方向、对称轴和顶点.探究新知怎样移动抛物线 就可以得到抛物线 ?还有其他平移方法吗?向左平移1个单位向下平移1个单位二次函数y=a(x-h)2+k的图象和性质举一反三特殊一般(1)当a>0,开口向上;当a<0,开口向下.(2)对称轴是x=h.(3)顶点坐标是(h,k).抛物线y=a(x-h)2+k有如下特点:一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k,平移的方向、距离要根据h,k的值来决定.hhkky=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k上下平移左右平移上下平移左右平移课堂小结当a>0,开口向上;当a<0,开口向下.对称轴是x=h.顶点坐标是(h,k).谢谢聆听
22.1 二次函数的图像和性质
22.1.3 二次函数y=a(x-h) +k的图象和性质
九年级-上册-第二十二章
目录
CONTENTS
课前导入
二次函数的图像和性质
二次函数y=a(x-h) +k(a≠0)的图象和性质
课前导入二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
开口方向
对称轴 x=h
顶点坐标 (h,k)
增减性
最值 y=k
(h,k)
x=h
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
开口方向
a>0,开口向上,并向上无限延伸
a<0,开口向下,并向下无限延伸
开口大小
|a|越大,开口越小
|a|越小,开口越大
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
对称轴: x=h
顶点坐标: (h,k)
最值
a>0时,最小值y=k
a<0时,最大值y=k
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
知识讲解
难点突破
二次函数y=a(x-h) +k(a≠0)
二次函数y=a(x-h) +k(a≠0)的图象和性质
a>0
x>h时,即在对称轴的右侧,y随x的增大而增大
x
x>h时,即在对称轴的右侧,y随x的增大而减小
x
课堂练习
难点巩固
二次函数y=a(x-h) +k(a≠0)的图象和性质
对于抛物线y= -(x+1) +3,有以下结论: ①抛物线的开口向下; ②对称轴为直线x=1; ③顶点坐标为(-1,3); ④x>-1时,y随x的增大而减小;⑤最小值是3.其中正确的结论有 .
【课堂小结】
小结反思
二次函数y=a(x-h) +k(a≠0)的图象和性质
性质a 图像 开口方向 顶点坐标 对称轴 最值 增减性 对称轴左侧 对称轴右侧
a>0 向上 (h,k) x=h 最小值y=k y随x增大而减小
y随x增大而增大
a<0 向下 最大值y=k y随x增大而增大
y随x增大而减小
二次函数y=a(x-h) +k(a≠0)的图象和性质:
新疆教科研
微信公众号
22.1.3 二次函数y=a(x-h)2+k的图象和性质
(第2课时)
学习目标1.通过观察二次函数y=a(x-h)2+k(a≠0)的图象,得到抛物线的开口方向、对称轴和顶点坐标.2.理解抛物线y=a(x-h)2+k与y=ax2之间的关系.yxOyxOyxOyxOyxOyxOyxOyxOyxOyxO温故知新(1)y=ax2(2)y=ax2+k(3)y=a(x-h)2x=hx=hx=hx=h(0,k)(0,k)(0,k)(0,k)(h,0)(h,0)(h,0)(h,0)探究新知例3画出函数 的图像,并指出它的开口方向、对称轴和顶点.…………210-1-2-3-4x解:先列表-5.5-3-1.5-1-1.5-3-5.512345x-1-2-3-4-5-6-7-8-91yO-1-2-3-4-5-10然后描点画图,函数的图像如图所示.x=-1抛物线 的开口向下,对称轴是x=-1,顶点坐标是(-1,-1).(-1,-1)二次函数y=a(x-h)2+k的图象和性质12345x-1-2-3-4-5-6-7-8-91yO-1-2-3-4-5-10例3画出函数 的图像,并指出它的开口方向、对称轴和顶点.怎样移动抛物线 就可以得到抛物线 ?向左平移1个单位向下平移1个单位二次函数y=a(x-h)2+k的图象和性质探究新知12345x-1-2-3-4-5-6-7-8-91yO-1-2-3-4-5-10例3画出函数 的图像,并指出它的开口方向、对称轴和顶点.探究新知怎样移动抛物线 就可以得到抛物线 ?还有其他平移方法吗?向左平移1个单位向下平移1个单位二次函数y=a(x-h)2+k的图象和性质举一反三特殊一般(1)当a>0,开口向上;当a<0,开口向下.(2)对称轴是x=h.(3)顶点坐标是(h,k).抛物线y=a(x-h)2+k有如下特点:一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向左(右)平移,可以得到抛物线y=a(x-h)2+k,平移的方向、距离要根据h,k的值来决定.hhkky=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k上下平移左右平移上下平移左右平移课堂小结当a>0,开口向上;当a<0,开口向下.对称轴是x=h.顶点坐标是(h,k).谢谢聆听
同课章节目录
