河南省郑州市中牟县第二高级中学2022-2023学年高二上学期8月开学考试数学试题(Word版含答案)
文档属性
| 名称 | 河南省郑州市中牟县第二高级中学2022-2023学年高二上学期8月开学考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 775.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-26 22:53:40 | ||
图片预览



文档简介
中牟县第二高级中学2022-2023学年高二上学期8月开学考试
(数学)
一 选择题
1.若集,则( )
A. B. C. D.
2.若,则复数的共轭复数是( )
A. B. C. D.
3.在中,点在边上,.记,则( )
A. B.
C. D.
4.已知某人射击每次击中目标的概率都是0.6,现采用随机模拟的方法估计其3次射击至少2次击中目标的概率P.先由计算器产生0到9之间的整数值的随机数,指定0 1 2 3 4 5表示击中目标,6 7 8 9表示未击中目标.因为射击3次,所以每3个随机数为一组,代表3次射击的结果.经随机模拟产生了以下20组随机数:
据此估计P的值为( )
A.0.6 B.0.65 C.0.7 D.0.75
5.在中,内角所对的边分别为.若,且的面积是1,则的外接圆的面积为( )
A. B. C. D.
6.某中学组织物理 化学学科竞赛,全校1000名学生都参加两科考试,考试后按学科分别评出一 二 三等奖和淘汰的这四个等级,现有某考场的两科考试数据统计如下,其中物理科目成绩为二等奖的考生有12人.如果以这个考场考生的物理和化学成绩去估计全校考生的物理和化学成绩分布,则以下说法正确的是( )
①该考场化学考试获得一等奖的有4人;
②全校物理考试获得二等奖的有240人;
③如果采用分层抽样从全校抽取200人,则化学考试被淘汰78人.
A.①②③ B.②③ C.①② D.①③
7.已知三棱锥的所有顶点都在球的球面上,且平面,,则球的表面积为( )
A. B. C. D.
8.把函数图像上所有点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到函数的图像,则( )
A. B. C.. D.
9.已知a,b是两条不同的直线,,,是三个不同的平面.给出下列命题:
①若,,,则或;
②若,,,则;
③若,,,则;
④“若,,则”是随机事件;
⑤若a,b是异面直线,则存在平面过直线a且垂直于直线b.
其中正确的命题是( )
A.①③ B.②⑤ C.③④ D.②④
10.已知,如果是的充分不必要条件,则实数的取值范围是( )
A. B. C. D.
11.已知,则( )
A. B. C. D.
12.在中,角所对的边分别是是边上一点,且,则的最小值是( )
A.4 B.6 C.8 D.9
二 填空题:
13.已知正方形的边长为,则__________.
14.已知函数,则__________.,函数的零点为__________.
15.甲 乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时该队获胜,比赛结束),根据以往比赛成绩,甲队的主客场安排依次为“主主客客主客主”,设甲队主场取胜的概率为0.8,客场取胜的概亭为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是__________.
16.如图,直三棱柱中,,点分别是棱的中点,一只蚂蚁从点出发,绕过三棱柱的一条棱爬到点处,则这只蚂蚁爬行的最短路程是__________.
三 解答题
17.(10分)已知是平面上两个不共线的向量且
(1)若方向相反,求的值;
(2)若三点共线,求的值.
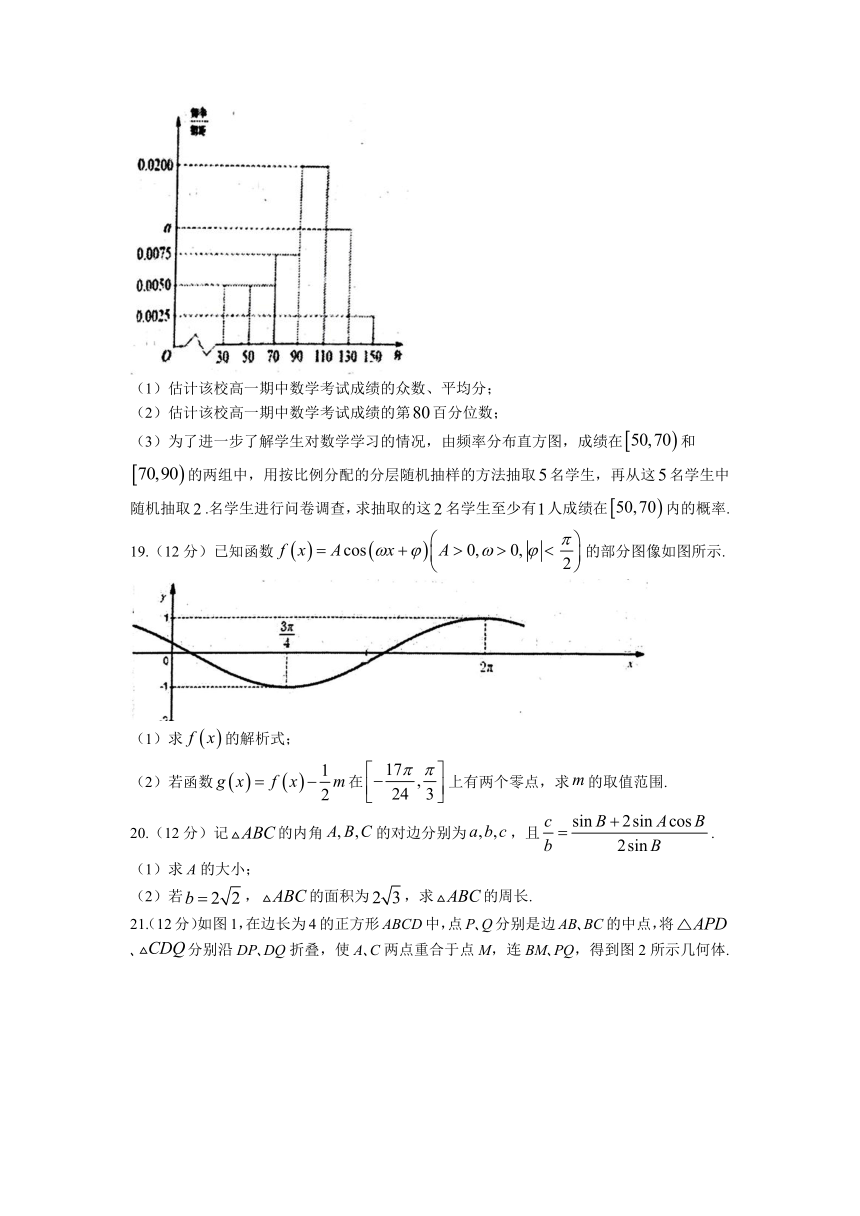
18.(12分)某校对年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取名学生,将分数按照,,,,,分成组,制成了如图所示的频率分布直方图:
(1)估计该校高一期中数学考试成绩的众数、平均分;
(2)估计该校高一期中数学考试成绩的第百分位数;
(3)为了进一步了解学生对数学学习的情况,由频率分布直方图,成绩在和的两组中,用按比例分配的分层随机抽样的方法抽取名学生,再从这名学生中随机抽取.名学生进行问卷调查,求抽取的这名学生至少有人成绩在内的概率.
19.(12分)已知函数的部分图像如图所示.
(1)求的解析式;
(2)若函数在上有两个零点,求的取值范围.
20.(12分)记的内角的对边分别为,且.
(1)求A的大小;
(2)若,的面积为,求的周长.
21.(12分)如图1,在边长为4的正方形ABCD中,点P Q分别是边AB BC的中点,将 分别沿DP DQ折叠,使A C两点重合于点M,连BM PQ,得到图2所示几何体.
(1)求证:;
(2)在线段MD上是否存在一点F,使平面PQF,如果存在,求的值,如果不存在,说明理由.
22.(12分)郑州市某地铁项目正在紧张建设中,通车后将给更多市民出行带来便利,已知该线路通车后,地铁的发车时间间隔t(单位:分钟)满足,,经测算,在某一时段,地铁载客量与发车时间间隔t相关,当时地铁可达到满载状态,载客量为1200人,当时,载客量会减少,减少的人数与的平方成正比,且发车时间间隔为2分钟时载客量为560人,记地铁载客量为.
(1)求的解析式;
(2)若该时段这条线路每分钟的净收益为(元),问当发车时间间隔为多少时,该时段这条线路每分钟的净收益最大?
中牟县第二高级中学2022-2023学年高二上学期8月开学考试
数学参考解析
一 选择题
1.B 2.C 3.A 4.B 5.B 6.C
7.D 8.A 9.D 10.A 11.D 12.C
二 填空题
13.解析:.
14.答案①;② 15. 16.
三 解答题
17.解析
(1)由题意知,,则存在,使得,即,
从而,得,或,又方向相反,则
(2)由题意知,,由三点共线得,存在,使得,即,从而,得或,所以或.
18.(1)估计该校高一期中数学考试成绩的众数、平均分:
解:由,得.数
数学成绩在:频率,频率,
频率,频率,
频率,频率,
分数在内的最多,所以众数是100
平均分是,
(2)解:由(1)知样本数据中数学考试成绩在分以下所占比例为,
在分以下所占比例为
因此,第百分位数一定位于内,由,
所以样本数据的第80百分位数约为115.
(3)由题意可知,分数段的人数为(人),
分数段的人数为(人).用按比例分配的分层随机抽样的方法抽取名学生,则需在内抽取2人,分別记为a,b,[70,90)内抽取3人,分別记为,设“从样本中抽取2人,至少有1人分数在内”为事件,则样本空间为,ay,az,bx,by,bz,共包今10个样本点,而事件,by,bz},包含7个样本点,
所以.即抽取的这2名学生至少有1人成绩在内的概率为
19.答案(1)(1)
解析(1)由图可知,由,得,
得.因为,所以,
得,又,所以,故.
(2)由题意可知,的图像与直线有两个交点.
因为,所以.
因为,,所以,
得,故的取值范围为.
20.解析(1)由正弦定理得,所以
得,因为,所以,
得,又,所以.
(2)由得,
山余弦定理得,
得,得,所以的周长为.
21.【解析】(1)证明:由图1可得
平面平面
平面
假设在线段上存在一点,使平面.
连交于点,连,由图1可得,即
平面平面,平面平面
22.答案(1);(2)分钟.
详解
(1)由题意可知,(k为常数),
因,则,
所以;
(2)由得,
即,
①当时,,当且仅当等号成立;
②当时,在[10,20]上递减,当时Q取最大值24,
由①②可知,当发车时间间隔为分钟时,该时段这条线路每分钟的净收益最大,最大为120元.
(数学)
一 选择题
1.若集,则( )
A. B. C. D.
2.若,则复数的共轭复数是( )
A. B. C. D.
3.在中,点在边上,.记,则( )
A. B.
C. D.
4.已知某人射击每次击中目标的概率都是0.6,现采用随机模拟的方法估计其3次射击至少2次击中目标的概率P.先由计算器产生0到9之间的整数值的随机数,指定0 1 2 3 4 5表示击中目标,6 7 8 9表示未击中目标.因为射击3次,所以每3个随机数为一组,代表3次射击的结果.经随机模拟产生了以下20组随机数:
据此估计P的值为( )
A.0.6 B.0.65 C.0.7 D.0.75
5.在中,内角所对的边分别为.若,且的面积是1,则的外接圆的面积为( )
A. B. C. D.
6.某中学组织物理 化学学科竞赛,全校1000名学生都参加两科考试,考试后按学科分别评出一 二 三等奖和淘汰的这四个等级,现有某考场的两科考试数据统计如下,其中物理科目成绩为二等奖的考生有12人.如果以这个考场考生的物理和化学成绩去估计全校考生的物理和化学成绩分布,则以下说法正确的是( )
①该考场化学考试获得一等奖的有4人;
②全校物理考试获得二等奖的有240人;
③如果采用分层抽样从全校抽取200人,则化学考试被淘汰78人.
A.①②③ B.②③ C.①② D.①③
7.已知三棱锥的所有顶点都在球的球面上,且平面,,则球的表面积为( )
A. B. C. D.
8.把函数图像上所有点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到函数的图像,则( )
A. B. C.. D.
9.已知a,b是两条不同的直线,,,是三个不同的平面.给出下列命题:
①若,,,则或;
②若,,,则;
③若,,,则;
④“若,,则”是随机事件;
⑤若a,b是异面直线,则存在平面过直线a且垂直于直线b.
其中正确的命题是( )
A.①③ B.②⑤ C.③④ D.②④
10.已知,如果是的充分不必要条件,则实数的取值范围是( )
A. B. C. D.
11.已知,则( )
A. B. C. D.
12.在中,角所对的边分别是是边上一点,且,则的最小值是( )
A.4 B.6 C.8 D.9
二 填空题:
13.已知正方形的边长为,则__________.
14.已知函数,则__________.,函数的零点为__________.
15.甲 乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时该队获胜,比赛结束),根据以往比赛成绩,甲队的主客场安排依次为“主主客客主客主”,设甲队主场取胜的概率为0.8,客场取胜的概亭为0.5,且各场比赛结果相互独立,则甲队以4:1获胜的概率是__________.
16.如图,直三棱柱中,,点分别是棱的中点,一只蚂蚁从点出发,绕过三棱柱的一条棱爬到点处,则这只蚂蚁爬行的最短路程是__________.
三 解答题
17.(10分)已知是平面上两个不共线的向量且
(1)若方向相反,求的值;
(2)若三点共线,求的值.
18.(12分)某校对年高一上学期期中数学考试成绩(单位:分)进行分析,随机抽取名学生,将分数按照,,,,,分成组,制成了如图所示的频率分布直方图:
(1)估计该校高一期中数学考试成绩的众数、平均分;
(2)估计该校高一期中数学考试成绩的第百分位数;
(3)为了进一步了解学生对数学学习的情况,由频率分布直方图,成绩在和的两组中,用按比例分配的分层随机抽样的方法抽取名学生,再从这名学生中随机抽取.名学生进行问卷调查,求抽取的这名学生至少有人成绩在内的概率.
19.(12分)已知函数的部分图像如图所示.
(1)求的解析式;
(2)若函数在上有两个零点,求的取值范围.
20.(12分)记的内角的对边分别为,且.
(1)求A的大小;
(2)若,的面积为,求的周长.
21.(12分)如图1,在边长为4的正方形ABCD中,点P Q分别是边AB BC的中点,将 分别沿DP DQ折叠,使A C两点重合于点M,连BM PQ,得到图2所示几何体.
(1)求证:;
(2)在线段MD上是否存在一点F,使平面PQF,如果存在,求的值,如果不存在,说明理由.
22.(12分)郑州市某地铁项目正在紧张建设中,通车后将给更多市民出行带来便利,已知该线路通车后,地铁的发车时间间隔t(单位:分钟)满足,,经测算,在某一时段,地铁载客量与发车时间间隔t相关,当时地铁可达到满载状态,载客量为1200人,当时,载客量会减少,减少的人数与的平方成正比,且发车时间间隔为2分钟时载客量为560人,记地铁载客量为.
(1)求的解析式;
(2)若该时段这条线路每分钟的净收益为(元),问当发车时间间隔为多少时,该时段这条线路每分钟的净收益最大?
中牟县第二高级中学2022-2023学年高二上学期8月开学考试
数学参考解析
一 选择题
1.B 2.C 3.A 4.B 5.B 6.C
7.D 8.A 9.D 10.A 11.D 12.C
二 填空题
13.解析:.
14.答案①;② 15. 16.
三 解答题
17.解析
(1)由题意知,,则存在,使得,即,
从而,得,或,又方向相反,则
(2)由题意知,,由三点共线得,存在,使得,即,从而,得或,所以或.
18.(1)估计该校高一期中数学考试成绩的众数、平均分:
解:由,得.数
数学成绩在:频率,频率,
频率,频率,
频率,频率,
分数在内的最多,所以众数是100
平均分是,
(2)解:由(1)知样本数据中数学考试成绩在分以下所占比例为,
在分以下所占比例为
因此,第百分位数一定位于内,由,
所以样本数据的第80百分位数约为115.
(3)由题意可知,分数段的人数为(人),
分数段的人数为(人).用按比例分配的分层随机抽样的方法抽取名学生,则需在内抽取2人,分別记为a,b,[70,90)内抽取3人,分別记为,设“从样本中抽取2人,至少有1人分数在内”为事件,则样本空间为,ay,az,bx,by,bz,共包今10个样本点,而事件,by,bz},包含7个样本点,
所以.即抽取的这2名学生至少有1人成绩在内的概率为
19.答案(1)(1)
解析(1)由图可知,由,得,
得.因为,所以,
得,又,所以,故.
(2)由题意可知,的图像与直线有两个交点.
因为,所以.
因为,,所以,
得,故的取值范围为.
20.解析(1)由正弦定理得,所以
得,因为,所以,
得,又,所以.
(2)由得,
山余弦定理得,
得,得,所以的周长为.
21.【解析】(1)证明:由图1可得
平面平面
平面
假设在线段上存在一点,使平面.
连交于点,连,由图1可得,即
平面平面,平面平面
22.答案(1);(2)分钟.
详解
(1)由题意可知,(k为常数),
因,则,
所以;
(2)由得,
即,
①当时,,当且仅当等号成立;
②当时,在[10,20]上递减,当时Q取最大值24,
由①②可知,当发车时间间隔为分钟时,该时段这条线路每分钟的净收益最大,最大为120元.
同课章节目录
