12.3角的平分线的性质(2)
文档属性
| 名称 | 12.3角的平分线的性质(2) |
|
|
| 格式 | zip | ||
| 文件大小 | 124.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-24 00:00:00 | ||
图片预览


文档简介
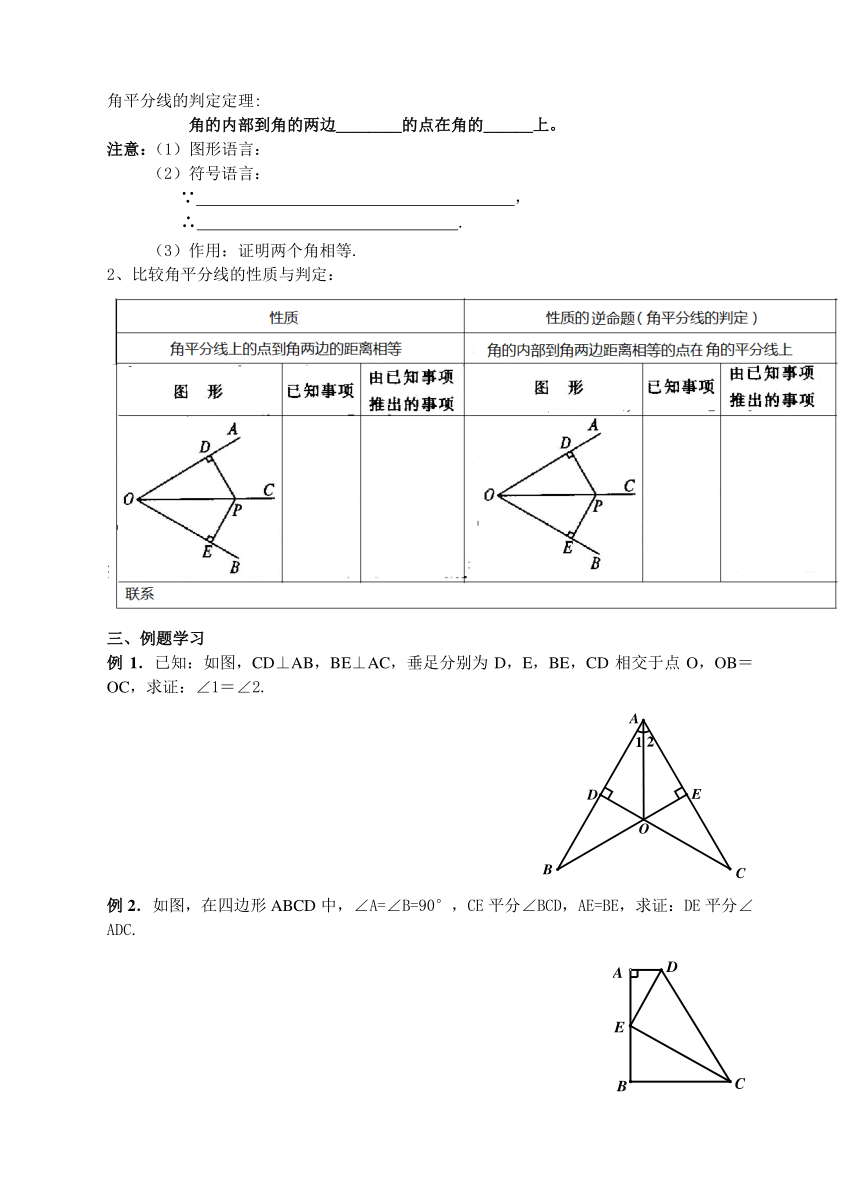
12.3角的平分线的性质(2)
学习目标:
1.会叙述角平分线的性质及角平分线的判定:到角的两边距离相等的点在角的平分线上;
2.能利用角平分线的性质及角平分线的判定解决一些实际问题.
学习重点:角平分线的性质及判定的应用
学习难点:利用性质及判定解决一些实际问题
学习方法:探索归纳法
一、复习旧知——角平分线的性质定理
1.角平分线的性质:角平分线上的点到角的 的距离 .
2.几何语言:(注意:三个已知条件缺一不可)
∵ ,
∴ .
3、用尺规作出三角形三个内角的平分线:
你发现了什么特点吗?
4.如图,△ABC的角平分线BM,CN相交于点P,
求证,点P到三边AB,BC,CA的距离相等.
二、探究新知:
1.求证:到角的两边的距离相等的点在角的平分线上.
已知:
求证:
证明:
角平分线的判定定理:
角的内部到角的两边____的点在角的___上。
注意:(1)图形语言:
(2)符号语言:
∵ ,
∴ .
(3)作用:证明两个角相等.
2、比较角平分线的性质与判定:
三、例题学习
例1.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证:∠1=∠2.
例2.如图,在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE,求证:DE平分∠ADC.
四、应用新知 解决问题:
如图,要在S区建一个集贸市场,使它到公路、铁路距离相等,并且离
公路与铁路的交叉处500米,这个集贸市场应建在何处?(在图上标出它的位置,比例尺 1:20 000)
【课堂训练】
1.已知△ABC中,∠A=60°,∠ABC,∠ACB的平分线交于点O,则∠BOC的度数为 .
2.到三角形三条边的距离相等的点是( )
A、三条中线的交点 B、三条高线的交点
C、三条边的垂直平分线的交点 D、三条角平分线的交点
3.已知的平分线上一点,到的距离为,则到的距离为
.
4.如图,的两个外角平分线相交于点,则下面结论正确的是( )
A.AB=AC B.平分 C.平分 D.
第4题 第5题 第6题
5.如图,的三边、、的长分别为20、30、40,其三条角平分线的交点为,则 .
6.如图,在△ABC中,BD为∠ABC的平分线,DE⊥AB于点E,且DE=2cm,AB=9cm,BC=6cm,则△ABC的面积为 .
7.在中,,是的角平分线,若,,则点到的距离为 .
8.如图,在直线上求作一点, 使得点到射线和的距离相等.
9.已知:如图,∠C=∠D=90°,AC=AD.求证:(1)∠ABC=∠ABD;(2) BC=BD.
10.已知:如图,D是△ABC外角∠ACE的角平分线,DF⊥AC于E,DE⊥BC交BC的延长线于E,求证:CE=CF .
11. 如图,,于,于.
⑴求证:在的平分线上;
⑵若将⑴的条件“”和结论“在的平分线上”互换,成立吗?说明理由.
【课堂训练】答案:
1. 120°.
2. D.
3. 1.5.
4. B.
5. 6∶4∶3.
6. 15 cm2.
7. 2 cm.
8. 图略(提示:作∠AOB的角平分线,交直线于,则点即为所求)
9. 证明:(1)∵∠C=∠D=90°,
∴BC⊥AC ,BD⊥AD.
∵AC=AD,
∴点A在∠CBD的角平分线上,
∴∠ABC=∠ABD.
(2)∵∠C=∠D=90°,∠ABC=∠ABD,
∴∠BAC=∠BAD.
∵BC⊥AC ,BD⊥AD,
∴BC=BD.
10. 证明:∵CD平分∠ACE,DF⊥AC,DE⊥BC,
∴∠DFC=∠DEC, ∠DCF=∠DCE,
∴∠FDC=∠EDC.
∵DF⊥AC,DE⊥BC,
∴CE=CF .
11. (1)证明:∵,,
∴∠BED=∠CFD=90°.
在△BED和△CFD中,
∵
∴△BED≌Rt△CFD(AAS).
∴DE=DF,
∴在的平分线上.
(2)成立.
证明:∵在的平分线上,,,
∴DE=DF, ∠BED=∠CFD=90°.
在△BED和△CFD中,
∵
∴△BED≌Rt△CFD(AAS).
∴BD=CD.
12. 解:∵
OD=2 cm.
13.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学习目标:
1.会叙述角平分线的性质及角平分线的判定:到角的两边距离相等的点在角的平分线上;
2.能利用角平分线的性质及角平分线的判定解决一些实际问题.
学习重点:角平分线的性质及判定的应用
学习难点:利用性质及判定解决一些实际问题
学习方法:探索归纳法
一、复习旧知——角平分线的性质定理
1.角平分线的性质:角平分线上的点到角的 的距离 .
2.几何语言:(注意:三个已知条件缺一不可)
∵ ,
∴ .
3、用尺规作出三角形三个内角的平分线:
你发现了什么特点吗?
4.如图,△ABC的角平分线BM,CN相交于点P,
求证,点P到三边AB,BC,CA的距离相等.
二、探究新知:
1.求证:到角的两边的距离相等的点在角的平分线上.
已知:
求证:
证明:
角平分线的判定定理:
角的内部到角的两边____的点在角的___上。
注意:(1)图形语言:
(2)符号语言:
∵ ,
∴ .
(3)作用:证明两个角相等.
2、比较角平分线的性质与判定:
三、例题学习
例1.已知:如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证:∠1=∠2.
例2.如图,在四边形ABCD中,∠A=∠B=90°,CE平分∠BCD,AE=BE,求证:DE平分∠ADC.
四、应用新知 解决问题:
如图,要在S区建一个集贸市场,使它到公路、铁路距离相等,并且离
公路与铁路的交叉处500米,这个集贸市场应建在何处?(在图上标出它的位置,比例尺 1:20 000)
【课堂训练】
1.已知△ABC中,∠A=60°,∠ABC,∠ACB的平分线交于点O,则∠BOC的度数为 .
2.到三角形三条边的距离相等的点是( )
A、三条中线的交点 B、三条高线的交点
C、三条边的垂直平分线的交点 D、三条角平分线的交点
3.已知的平分线上一点,到的距离为,则到的距离为
.
4.如图,的两个外角平分线相交于点,则下面结论正确的是( )
A.AB=AC B.平分 C.平分 D.
第4题 第5题 第6题
5.如图,的三边、、的长分别为20、30、40,其三条角平分线的交点为,则 .
6.如图,在△ABC中,BD为∠ABC的平分线,DE⊥AB于点E,且DE=2cm,AB=9cm,BC=6cm,则△ABC的面积为 .
7.在中,,是的角平分线,若,,则点到的距离为 .
8.如图,在直线上求作一点, 使得点到射线和的距离相等.
9.已知:如图,∠C=∠D=90°,AC=AD.求证:(1)∠ABC=∠ABD;(2) BC=BD.
10.已知:如图,D是△ABC外角∠ACE的角平分线,DF⊥AC于E,DE⊥BC交BC的延长线于E,求证:CE=CF .
11. 如图,,于,于.
⑴求证:在的平分线上;
⑵若将⑴的条件“”和结论“在的平分线上”互换,成立吗?说明理由.
【课堂训练】答案:
1. 120°.
2. D.
3. 1.5.
4. B.
5. 6∶4∶3.
6. 15 cm2.
7. 2 cm.
8. 图略(提示:作∠AOB的角平分线,交直线于,则点即为所求)
9. 证明:(1)∵∠C=∠D=90°,
∴BC⊥AC ,BD⊥AD.
∵AC=AD,
∴点A在∠CBD的角平分线上,
∴∠ABC=∠ABD.
(2)∵∠C=∠D=90°,∠ABC=∠ABD,
∴∠BAC=∠BAD.
∵BC⊥AC ,BD⊥AD,
∴BC=BD.
10. 证明:∵CD平分∠ACE,DF⊥AC,DE⊥BC,
∴∠DFC=∠DEC, ∠DCF=∠DCE,
∴∠FDC=∠EDC.
∵DF⊥AC,DE⊥BC,
∴CE=CF .
11. (1)证明:∵,,
∴∠BED=∠CFD=90°.
在△BED和△CFD中,
∵
∴△BED≌Rt△CFD(AAS).
∴DE=DF,
∴在的平分线上.
(2)成立.
证明:∵在的平分线上,,,
∴DE=DF, ∠BED=∠CFD=90°.
在△BED和△CFD中,
∵
∴△BED≌Rt△CFD(AAS).
∴BD=CD.
12. 解:∵
OD=2 cm.
13.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
