第二十三章 旋转单元检测试题(含答案)
文档属性
| 名称 | 第二十三章 旋转单元检测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 417.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 11:12:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.在平面直角坐标系中,已知点和点,则A、B两点( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线对称
4.已知点与点关于原点对称,则a与b的值分别为( )
A.-3;1 B.-1;3 C.1;-3 D.3;-1
5.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A.3 B.2.5 C.4 D.2
6.下列说法中错误的是( )
A.成中心对称的两个图形全等
B.成中心对称的两个图形中,对称点的连线被对称轴平分
C.中心对称图形的对称中心是对称点连线的中心
D.中心对称图形绕对称中心旋转180°后,都能与自身重合
7.如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30° B.40° C.50° D.60°
8.如图,把△ABC绕B点逆时针方旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=( )
A.52° B.64° C.77° D.82°
9.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( )
A.68° B.20° C.28° D.22°
10. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点为中心( ).
A.顺时针旋转得到 B.顺时针旋转得到
C.逆时针旋转得到 D.逆时针旋转得到
二、填空题(每题3分,共24分)
11.已知点M(a,2)与点N(1,b)关于原点成中心对称,则2a+b的值为 ___.
12.在平面直角坐标系中,点(﹣2,3)关于原点对称的点的坐标是 .
13. 若数字串“000”和数字串“101”既是轴对称图形,又是中心对称图形,那么数字串“110”是 图形(填写“轴对称”、“中心对称”).
14. 如图所示,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=_____.
15. 如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,则∠EAF=_____.
16. 已知点A(a, 1) 与点B(5, b)是关于原点O的对称点,则a= ,b= .
17. 如图,O是等边△ABC内一点,将△AOB绕B点逆时针旋转,使得B、O两点的对应点分别为C、D,则旋转角为_____________,图中除△ABC外,还有等边三形是______.
18.如图,点O是 ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
20.请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
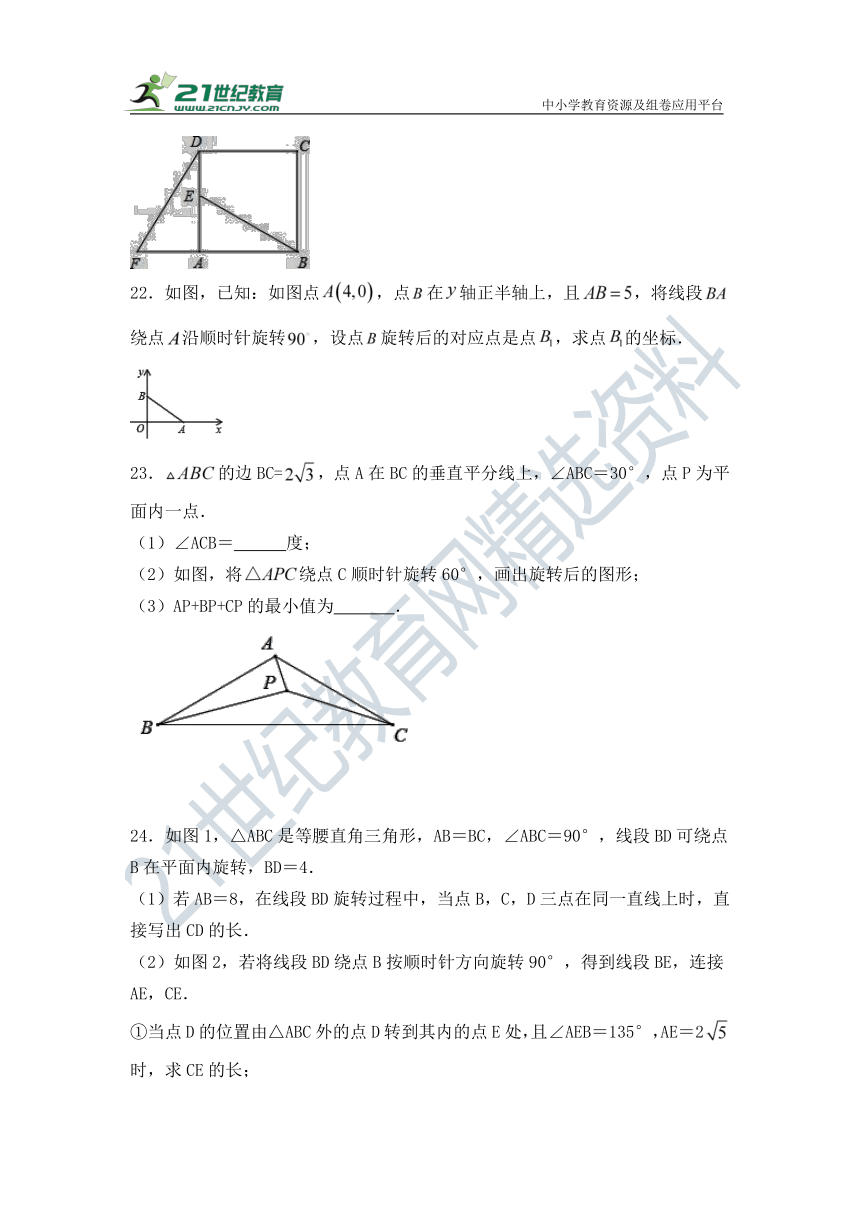
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.的边BC=,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 度;
(2)如图,将绕点C顺时针旋转60°,画出旋转后的图形;
(3)AP+BP+CP的最小值为 .
24.如图1,△ABC是等腰直角三角形,AB=BC,∠ABC=90°,线段BD可绕点B在平面内旋转,BD=4.
(1)若AB=8,在线段BD旋转过程中,当点B,C,D三点在同一直线上时,直接写出CD的长.
(2)如图2,若将线段BD绕点B按顺时针方向旋转90°,得到线段BE,连接AE,CE.
①当点D的位置由△ABC外的点D转到其内的点E处,且∠AEB=135°,AE=2时,求CE的长;
②如图3,若AB=8,连接DE,将△BDE绕点B在平面内旋转,分别取DE,AE,AC的中点M,P,N,连接MP,PN,NM,请直接写出△MPN面积S的取值范围.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B C B C B C D D
二、填空题(每题3分,共24分)
11.-4
12.解:点(﹣2,3)关于原点对称的点的坐标为(2,﹣3).
故答案是:(2,﹣3).
13. 解:根据对称图形的概念,知110仅是轴对称图形,对称轴为正中水平直线.
14. 【答案】60°
15. 【答案】45°
16. 【答案】a= -5 ,b= -1
17. 【答案】60°;△AOD
18.解:连接AO、BO、CO,
∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是 ABCD的对称中心,
∴S△AOB=S△BOC=S ABCD,
∴==.
即S1与S2之间的等量关系是=.
故答案为=.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
20.解:如图所示:
.
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.(1)∵点A在BC的垂直平分线上,
∴AB=AC,
∴∠ACB=∠ABC=30°,
故答案为:30;
(2)如图:
(3)如图,连接、AB、A,
由旋转得AP=A,PC=C,AC=C,∠AC=∠PC=60°,
∴△PC、△AC都是等边三角形,
∴PC=P,∠AC=60°,
∵∠ACB=∠ABC=30°,
∴∠AC=∠ACB+∠ABC,即B、A、三点共线,
∵∠CB=∠CA+∠ACB=90°,∠BC=60°,BC=,
∴B=,
当B、P、、四点共线时,AP+BP+CP=PB++A值的最小,
∴AP+BP+CP=B=4,
故答案为:4.
24.解:(1)当点D在CB的延长线上时,CD=4+8=12,
当点D在线段BC上时,CD=8﹣4=4,
故CD的长为4或12.
(2)①如图2中,连接AD,DE.
∵BD=BE=4,∠DBE=90°,
∴,∠DEB=45°,
∵∠AEB=135°,
∴∠AED=90°,
∵,
∴
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴.
②如图3中,连接AD,延长CE交AB于O,交AD于J.
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴EC=AD,∠DAB=∠ECB,
∵∠BOC+∠BCE=90°,∠AOJ=∠BOC,
∴∠AOJ+∠DAB=90°,
∴∠AJC=90°,
∴CJ⊥AD,
∵AP=EP,EM=MD,
∴PM∥AD,,
同法可得,PN∥EC,,
∴PM=PN,PM⊥JC,
∴PN⊥PM,
∴△PMN是等腰直角三角形,
∴
∵4≤AD≤12,
∴2≤S△PMN≤18.
第二十三章 《旋转》单元测试卷
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分,共30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.在平面直角坐标系中,已知点和点,则A、B两点( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线对称
4.已知点与点关于原点对称,则a与b的值分别为( )
A.-3;1 B.-1;3 C.1;-3 D.3;-1
5.如图,在矩形ABCD中,AB=5,BC=6,点E在BC边上,且BE=2,F为AB边上的一个动点,连接EF,以EF为边作等边△EFG,且点G在矩形ABCD内,连接CG,则CG的最小值为( )
A.3 B.2.5 C.4 D.2
6.下列说法中错误的是( )
A.成中心对称的两个图形全等
B.成中心对称的两个图形中,对称点的连线被对称轴平分
C.中心对称图形的对称中心是对称点连线的中心
D.中心对称图形绕对称中心旋转180°后,都能与自身重合
7.如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30° B.40° C.50° D.60°
8.如图,把△ABC绕B点逆时针方旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=( )
A.52° B.64° C.77° D.82°
9.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=112°,则∠α的大小是( )
A.68° B.20° C.28° D.22°
10. 同学们曾玩过万花筒,它是由三块等宽等长的玻璃围成的,图是看到的万花筒的一个图案,图中所有的小三角形均是全等的等边三角形,其中的菱形可以看成是把菱形以点为中心( ).
A.顺时针旋转得到 B.顺时针旋转得到
C.逆时针旋转得到 D.逆时针旋转得到
二、填空题(每题3分,共24分)
11.已知点M(a,2)与点N(1,b)关于原点成中心对称,则2a+b的值为 ___.
12.在平面直角坐标系中,点(﹣2,3)关于原点对称的点的坐标是 .
13. 若数字串“000”和数字串“101”既是轴对称图形,又是中心对称图形,那么数字串“110”是 图形(填写“轴对称”、“中心对称”).
14. 如图所示,P是等边△ABC内一点,△BMC是由△BPA旋转所得,则∠PBM=_____.
15. 如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,则∠EAF=_____.
16. 已知点A(a, 1) 与点B(5, b)是关于原点O的对称点,则a= ,b= .
17. 如图,O是等边△ABC内一点,将△AOB绕B点逆时针旋转,使得B、O两点的对应点分别为C、D,则旋转角为_____________,图中除△ABC外,还有等边三形是______.
18.如图,点O是 ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是 .
三.解答题(共46分,19题6分,20 ---24题8分)
19.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)哪两个图形成中心对称?
(2)已知△ADC的面积为4,求△ABE的面积;
(3)已知AB=5,AC=3,求AD的取值范围.
20.请在下列三个2×2的方格中,各画出一个三角形,要求所画三角形是图中三角形经过轴对称变换后得到的图形,且所画的三角形顶点与方格中的小正方形顶点重合,并将所画三角形涂上阴影.(注:所画的三个图形不能重复)
21.如图,四边形ABCD是正方形,△ADF绕着点A顺时旋转90°得到△ABE,若AF=4,AB=7.
(1)求DE的长度;
(2)指出BE与DF的关系如何?并说明由.
22.如图,已知:如图点,点在轴正半轴上,且,将线段绕点沿顺时针旋转,设点旋转后的对应点是点,求点的坐标.
23.的边BC=,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 度;
(2)如图,将绕点C顺时针旋转60°,画出旋转后的图形;
(3)AP+BP+CP的最小值为 .
24.如图1,△ABC是等腰直角三角形,AB=BC,∠ABC=90°,线段BD可绕点B在平面内旋转,BD=4.
(1)若AB=8,在线段BD旋转过程中,当点B,C,D三点在同一直线上时,直接写出CD的长.
(2)如图2,若将线段BD绕点B按顺时针方向旋转90°,得到线段BE,连接AE,CE.
①当点D的位置由△ABC外的点D转到其内的点E处,且∠AEB=135°,AE=2时,求CE的长;
②如图3,若AB=8,连接DE,将△BDE绕点B在平面内旋转,分别取DE,AE,AC的中点M,P,N,连接MP,PN,NM,请直接写出△MPN面积S的取值范围.
参考答案
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B C B C B C D D
二、填空题(每题3分,共24分)
11.-4
12.解:点(﹣2,3)关于原点对称的点的坐标为(2,﹣3).
故答案是:(2,﹣3).
13. 解:根据对称图形的概念,知110仅是轴对称图形,对称轴为正中水平直线.
14. 【答案】60°
15. 【答案】45°
16. 【答案】a= -5 ,b= -1
17. 【答案】60°;△AOD
18.解:连接AO、BO、CO,
∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是 ABCD的对称中心,
∴S△AOB=S△BOC=S ABCD,
∴==.
即S1与S2之间的等量关系是=.
故答案为=.
三.解答题(共46分,19题6分,20 ---24题8分)
19.解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8;
(3)∵在△ABD和△ECD中,,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵△ACE中,AB﹣AC<AE<AC+AB,
∴2<AE<8,
∴1<AD<4.
20.解:如图所示:
.
21.(1)3;(2)BE=DF,BE⊥DF.
【详解】
解:(1)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=AD﹣AE=7﹣4=3;
(2)BE、DF的关系为:BE=DF,BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°﹣90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE=DF,BE⊥DF.
22.点的坐标为.
【详解】
解:如图,作轴于,
∵,,
∴,
∵线段绕点沿逆时针旋转得,
∴,且,
∴
而,
∴,
在和中
,
∴,
∴,,
∴,
∴点的坐标为.
23.(1)∵点A在BC的垂直平分线上,
∴AB=AC,
∴∠ACB=∠ABC=30°,
故答案为:30;
(2)如图:
(3)如图,连接、AB、A,
由旋转得AP=A,PC=C,AC=C,∠AC=∠PC=60°,
∴△PC、△AC都是等边三角形,
∴PC=P,∠AC=60°,
∵∠ACB=∠ABC=30°,
∴∠AC=∠ACB+∠ABC,即B、A、三点共线,
∵∠CB=∠CA+∠ACB=90°,∠BC=60°,BC=,
∴B=,
当B、P、、四点共线时,AP+BP+CP=PB++A值的最小,
∴AP+BP+CP=B=4,
故答案为:4.
24.解:(1)当点D在CB的延长线上时,CD=4+8=12,
当点D在线段BC上时,CD=8﹣4=4,
故CD的长为4或12.
(2)①如图2中,连接AD,DE.
∵BD=BE=4,∠DBE=90°,
∴,∠DEB=45°,
∵∠AEB=135°,
∴∠AED=90°,
∵,
∴
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴.
②如图3中,连接AD,延长CE交AB于O,交AD于J.
∵∠DBE=∠ABC=90°,
∴∠DBA=∠EBC,
∵BD=BE,BA=BC,
∴△DBA≌△EBC(SAS),
∴EC=AD,∠DAB=∠ECB,
∵∠BOC+∠BCE=90°,∠AOJ=∠BOC,
∴∠AOJ+∠DAB=90°,
∴∠AJC=90°,
∴CJ⊥AD,
∵AP=EP,EM=MD,
∴PM∥AD,,
同法可得,PN∥EC,,
∴PM=PN,PM⊥JC,
∴PN⊥PM,
∴△PMN是等腰直角三角形,
∴
∵4≤AD≤12,
∴2≤S△PMN≤18.
同课章节目录
