第二十四章 圆单元检测试题（含答案）

中小学教育资源及组卷应用平台
第二十四章《圆》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每题3分，共30分)
1．下列命题是真命题的是（　　）
A．相等的弦所对的弧相等
B．圆心角相等，其所对的弦相等
C．在同圆或等圆中，圆心角不等，所对的弦不相等
D．弦相等，它所对的圆心角相等
2．在以下所给的命题中，正确的个数为（　　）
①直径是弦；②弦是直径；③半圆是弧，但弧不一定是半圆；④半径相等的两个半圆是等弧；⑤长度相等的弧是等弧．
A．1 B．2 C．3 D．4
3．已知⊙P的半径为5，P点的半径为（2，1），Q点的坐标为（0，6），则Q点的位置（　　）
A．在⊙P外 B．在⊙P上 C．在⊙P内 D．不能确定
4．如图所示的扇形的圆心角度数分别为30°，40°，50°，则剩下扇形是圆的（　　）
A． B． C． D．
5．如图，圆心为C、直径为MN的半圆上有不同的两点A、B，在CN上有一点P，∠CBP＝∠CAP＝10°，若的度数是40°，则的度数是（　　）
A．10° B．15° C．20° D．25°
6．75°的圆心角所对的弧长是2.5πcm，则此弧所在圆的半径是（　　）
A．6cm B．7cm C．8cm D．9cm
7．如图，点C是以AB为直径的圆上一个动点（不与点A、B重合），且AC+BC=12．若AB=m（m为整数），则整数m的值的个数为（ ）
A．0个 B．2个 C．3个 D．4个
8．如图，⊙O的弦AB＝16，M是AB的中点，且OM＝6，则⊙O的直径等于（　　）
A．12 B．16 C．20 D．24
9．如图，矩形的长为，宽为，点为矩形的中心，的半径为，于点，．若绕点按顺时针方向旋转，在旋转过程中，与矩形的边所在的直线相切的位置一共出现（ ）
A．次 B．次 C．次 D．次
10．如图，圆弧形弯道两边的直道在连接点处与弯道相切。测得，则这段圆弧弯道的度数为（ ）
A． B． C． D．
二、填空题(每题3分，共24分)
11．如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD=8，OE=3，则⊙O的半径为　 　．
12．点A、B在⊙O上，若∠AOB=40°，则∠OAB=　 　．
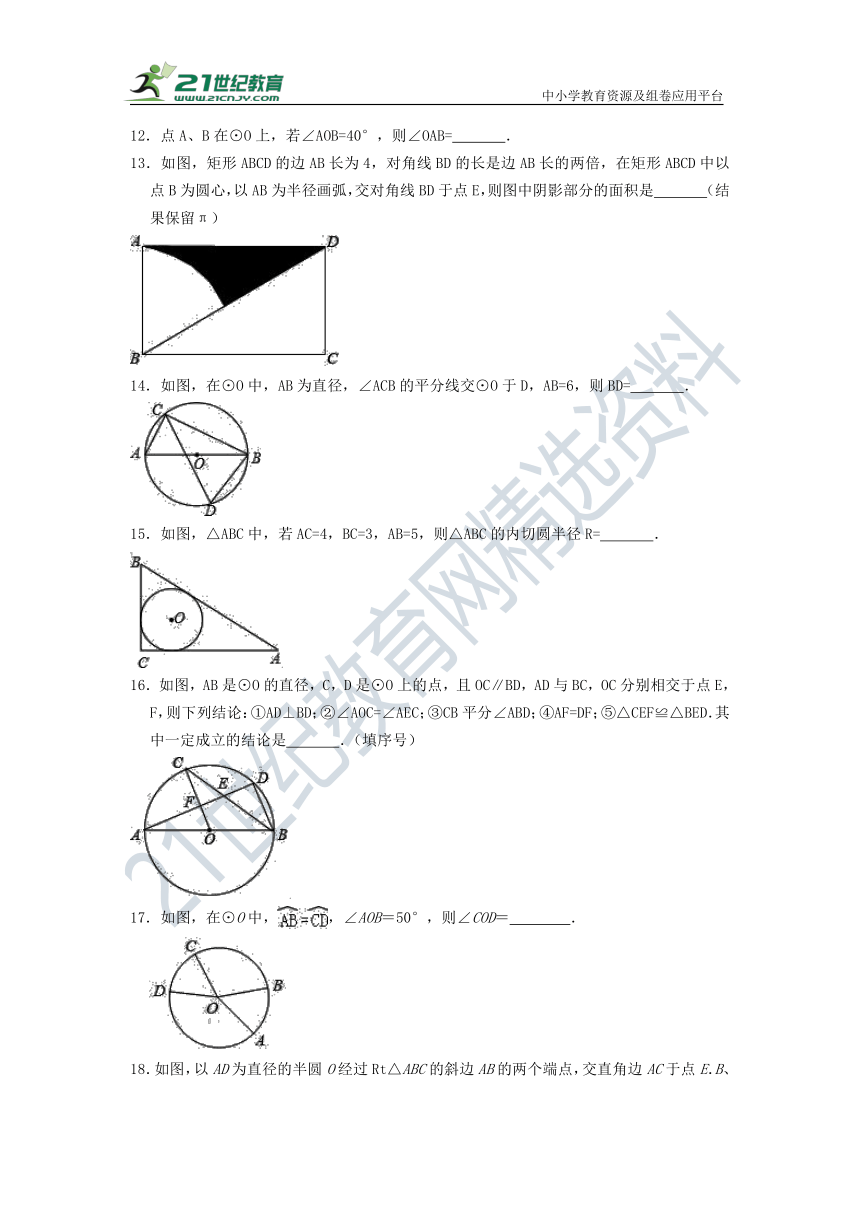
13．如图，矩形ABCD的边AB长为4，对角线BD的长是边AB长的两倍，在矩形ABCD中以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是　 　（结果保留π）
14．如图，在⊙O中，AB为直径，∠ACB的平分线交⊙O于D，AB=6，则BD=　 　．
15．如图，△ABC中，若AC=4，BC=3，AB=5，则△ABC的内切圆半径R=　 　．
16．如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD与BC，OC分别相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤△CEF≌△BED．其中一定成立的结论是　 　．（填序号）
17．如图，在⊙O中，，∠AOB＝50°，则∠COD＝　 　．
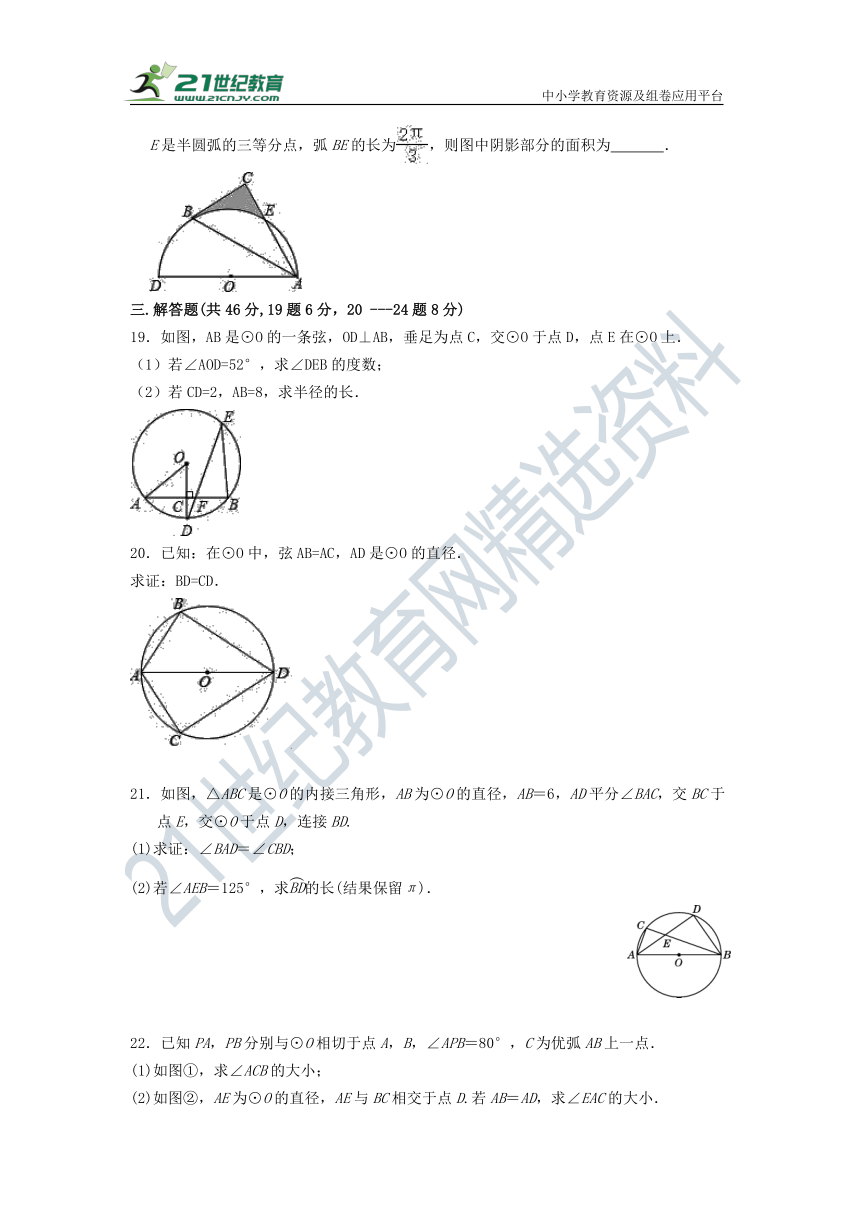
18．如图，以AD为直径的半圆O经过Rt△ABC的斜边AB的两个端点，交直角边AC于点E．B、E是半圆弧的三等分点，弧BE的长为，则图中阴影部分的面积为　 　．
三.解答题(共46分,19题6分，20 ---24题8分)
19．如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E在⊙O上．
（1）若∠AOD=52°，求∠DEB的度数；
（2）若CD=2，AB=8，求半径的长．
20．已知：在⊙O中，弦AB=AC，AD是⊙O的直径．
求证：BD=CD．
21．如图，△ABC是⊙O的内接三角形，AB为⊙O的直径，AB＝6，AD平分∠BAC，交BC于点E，交⊙O于点D，连接BD.
(1)求证：∠BAD＝∠CBD；
(2)若∠AEB＝125°，求的长(结果保留π)．
22．已知PA，PB分别与⊙O相切于点A，B，∠APB＝80°，C为优弧AB上一点．
(1)如图①，求∠ACB的大小；
(2)如图②，AE为⊙O的直径，AE与BC相交于点D.若AB＝AD，求∠EAC的大小．
23．我们在园林游玩时，常见到如图所示的圆弧形的门，若圆弧所在圆与地面BC相切于E点，四边形ABCD是一个矩形．已知AB＝米，BC＝1米．
（1）求圆弧形门最高点到地面的距离；
（2）求弧AMD的长．
24．如图，△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．
（1）试说明DF是⊙O的切线；
（2）若AC＝3AE，求的值．
参考答案
一、选择题(每题3分，共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C C A B D A C C C C
二、填空题(每题3分，共24分)
11．【解答】解：连接OD，
∵CD⊥AB于点E，直径AB过O，
∴DE=CE=CD=×8=4，∠OED=90°，
由勾股定理得：OD===5，
即⊙O的半径为5．
故答案为：5．
12．【解答】解：如图，
∵∠AOB=40°，OA=OB，
∴∠OAB=∠OBA==70°，
故答案为：70°．
13．【解答】解：∵矩形ABCD的边AB长为4，对角线BD的长是边AB长的两倍，
∴BD=8，∠ABE=60°，
∴S阴=S△ABD﹣S扇形BAE=×4×4﹣=8﹣π，
故答案为8﹣π．
14．【解答】解：
连接AD，
∵AB为⊙O直径，
∴∠ADB=∠ACB=90°，
∵CD平分∠ACB，
∴∠ACD=∠BCD==45°，
∴∠BAD=∠BCD=45°，∠ABD=∠ACD=45°，
即∠BAD=∠ABD，
∴AD=BD，
∵AB=6，
∴BD=AD=AB×sin45°=3，
故答案为：3．
15．【解答】解：∵AC=4，BC=3，AB=5，
∴AC2+BC2=AB2，
∴△ABC为直角三角形，∠ACB=90°，
∴△ABC的内切圆半径R===1．
故答案为1．
16．【解答】解：①∵AB是⊙O的直径，
∴∠ADB=90°，
∴AD⊥BD，
故①正确；
②∵∠AOC是⊙O的圆心角，∠AEC是⊙O的圆内部的角，
∴∠AOC≠∠AEC，
故②不正确；
③∵OC∥BD，
∴∠OCB=∠DBC，
∵OC=OB，
∴∠OCB=∠OBC，
∴∠OBC=∠DBC，
∴BC平分∠ABD，
故③正确；
④∵AB是⊙O的直径，
∴∠ADB=90°，
∴AD⊥BD，
∵OC∥BD，
∴∠AFO=90°，
∵点O为圆心，
∴AF=DF，
故④正确；
⑤∵△CEF和△BED中，没有相等的边，
∴△CEF与△BED不全等，
故⑤不正确；
综上可知：其中一定成立的有①③④，
故答案为：①③④．
17．解：∵＝，
∴∠COD＝∠AOB，
∵∠AOB＝50°，
∴∠COD＝50°，
故答案是：50°．
18．解：连接BD，BE，BO，EO，
∵B，E是半圆弧的三等分点，
∴∠EOA＝∠EOB＝∠BOD＝60°，
∴∠BAC＝∠EBA＝30°，
∴BE∥AD，
∵的长为，
∴＝，
解得：R＝2，
∴AB＝ADcos30°＝2，
∴BC＝AB＝，
∴AC＝＝＝3，
∴S△ABC＝×BC×AC＝××3＝，
∵△BOE和△ABE同底等高，
∴△BOE和△ABE面积相等，
∴图中阴影部分的面积为：S△ABC﹣S扇形BOE＝﹣＝﹣．
故答案为：．
三.解答题(共46分,19题6分，20 ---24题8分)
19．【解答】解：（1）连接OB，
∵OD⊥AB，
∴=，
∴∠BOD=∠AOD=52°，
∴∠DEB=∠BOD=26°；
（2）∵OD⊥AB，AB=8，
∴AC=CB=4，设半径为R，
在Rt△OAC中，R2=42+（R﹣2）2，
∴R=5．
∴⊙O的半径为5．
20．【解答】证明：∵AB=AC，
∴=，
∴∠ADB=∠ADC，
∵AD是⊙O的直径，
∴∠B=∠C=90°，
∴∠BAD=∠DAC，
∴=，
∴BD=CD．
21．(1)证明：∵AD平分∠BAC，
∴∠BAD＝∠CAD.
又∵∠CBD＝∠CAD，
∴∠BAD＝∠CBD.
(2)解：连接OD.
∵∠AEB＝125°，∴∠AEC＝55°.
∵AB为⊙O的直径，
∴∠ACE＝90°.
∴∠CAE＝35°.
∴∠DAB＝35°.
则所对圆心角∠DOB＝70°.
∴的长为＝π.
22．解：(1)连接OA，OB.
∵PA，PB是⊙O的切线，
∴∠OAP＝∠OBP＝90°.
∴∠AOB＝360°－90°－90°－80°＝100°.
∴∠ACB＝∠AOB＝50°.
(2)连接CE.
∵AE为⊙O的直径，∴∠ACE＝90°.
∵∠ACB＝50°，
∴∠BCE＝90°－50°＝40°.
∴∠BAE＝∠BCE＝40°.
∵AB＝AD，∴∠ABD＝∠ADB＝70°.
∴∠EAC＝∠ADB－∠ACB＝20°.
23．解：（1）设圆弧所在圆的圆心为O，
连接OE交AD于F，连接OA，如图所示：
设⊙O半径为x，
则OF＝x﹣米，AF＝米
在Rt△AOF中x2＝（）2+（x﹣）2
解得：x＝1
圆弧门最高点到地面的距离为2米．
（2）∵OA＝1，OF＝1﹣＝
∴∠AOF＝30°∴∠AOD＝60°（8分）
弧AMD的长＝＝米．
24．（1）证明：连接OD，
∵OB＝OD，
∴∠B＝∠ODB，
∵AB＝AC，
∴∠B＝∠C，
∴∠ODB＝∠C，
∴OD∥AC，
∵DF⊥AC，
∴OD⊥DF，
∴DF是⊙O的切线；
（2）解：连接BE，
∵AB是直径，
∴∠AEB＝90°，
∵AB＝AC，AC＝3AE，
∴AB＝3AE，CE＝4AE，
∴BE＝＝2AE，
在RT△BEC中，＝＝．