物理人教版(2019)选择性必修第一册1.2 动量定理(共34张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.2 动量定理(共34张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 12.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-08-27 09:56:46 | ||
图片预览











文档简介
(共34张PPT)
第1章 动量守恒定律
第2节 动量和动量定理
船靠岸时边缘上的废旧轮胎
见物思理:下列生活中的现象蕴含了什么奥秘?
摩托车头盔里的衬垫
跳高用的海绵垫
物体碰撞会受到力的作用,物体动量变化和力有什么关系?
汽车的安全气囊
气功表演:碎大石
情景及问题创设:在光滑水平面上的质量为 m 的物体在水平恒力 F 的作用下,经过时间 t,速度由 v 变为 v′ ,如何推导这几个量之间的关系?
可得Ft= mv′ - mv ,即Ft= p′ - p
解:如图所示,物体的初动量为 p= mv,末动量为p′ = mv′ ,
由加速度的定义式:
由牛顿第二定律F = ma = ,
理论推导
4.意义:(1)冲量是矢量,作用力的方向不变时其方向与力的方向相同。
(2 ) 冲量是过程量,反映了力对时间的积累效应。
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I=F Δt
3.单位:牛·秒(N·s)
若F为变力,如何求其冲量?
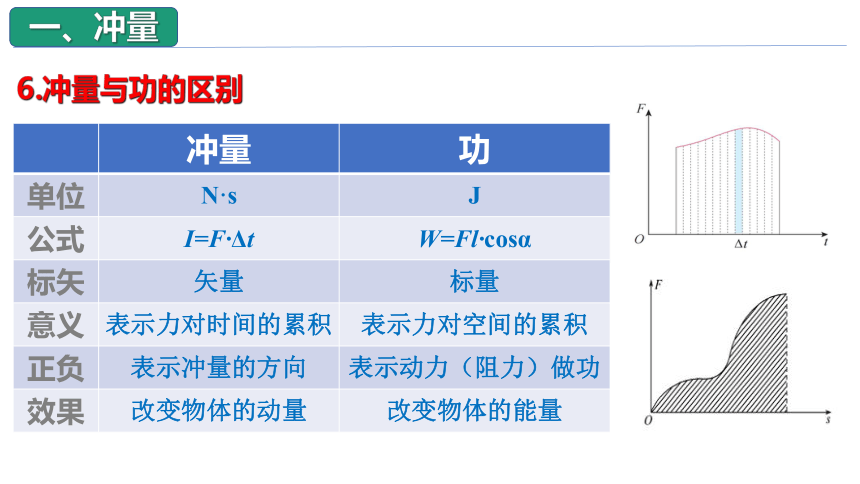
5.变力的冲量:
一、冲量
“面积”””
“冲量”
冲量 功
单位 N·s J
公式 I=F·Δt W=Fl·cosα
标矢 矢量 标量
意义 表示力对时间的累积 表示力对空间的累积
正负 表示冲量的方向 表示动力(阻力)做功
效果 改变物体的动量 改变物体的能量
一、冲量
6.冲量与功的区别
例1:
B
一、冲量
例2.质量为 m 的物体放在水平地面上,在与水平面成 角的拉力F 作用下由静止开始运动,经时间 t 速度达到 v,在这段时间内拉力 F 和重力 mg 冲量大小分别是 ( )
A.Ft,0
B.Ft cos , 0
C.mv, 0
D.Ft, mgt
D
F
v
mg
一、冲量
练习:如图所示,质量为2kg的物体沿倾角为30°高为h=5m的光滑斜面由静止从顶端下滑到底端的过程中 (g=10m/s2) ,求:
(1)重力的冲量;
(2)支持力的冲量;
(3)合外力的冲量.
mg
合外力的冲量IF合=F合·t=mgsin300 t=20N·s.
重力的冲量IG=mg·t=2×10×2N·s=40N·s.
支持力的冲量IF=F·t=mgcos300·t=20 N·s,
一、冲量
例3、A、B两个相同的物体,以相同的初速度分别在粗糙程度不同的水平面上运动,B物体先停下来,A物体又经较长时间停下来,下面的正确描述是( )
A、A物体受到的冲量大
B、B物体受到的冲量大
C、两个物体受到的冲量大小相等
D、这是不可能判断的
C
一、冲量
解:如图所示,物体的初动量为p=mv、末动量为 p、=mv` ,
由加速度的定义式
由牛顿第二定律 F=ma=
可得F t=mv ′ -mv ,即 F t =p ′ -p
1、内容:
2、公式:
Ft=mv'-mv
物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量.
3、说明:
①公式中的F指的是合外力,可以是恒力,可以是变力.
②公式表明合外力的冲量是动量变化的原因;
③动量定理公式是矢量式,计算时要先规定正方向,遵循平行四边形定则.
④动量定理不仅适用于宏观低速,同样适用于微观高速.
或
(过程量可通过状态量的变化来反映)
合力
末动量
初动量
二、动量定理
二、动量定理
例4、一个质量为0.18kg 的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s。球棒对垒球的平均作用力是多大?
解:沿垒球飞向球棒时的方向建立坐标轴,
垒球的初动量为
p=mv=0.18×25 kg·m/s=4.5kg·m/s
垒球的末动量为
p'=mv'=(-0.18)×25 kg·m/s=-8.1kg·m/s
垒球所受平均作用力大小为1260N,
力的方向与垒球飞来的方向相反
4、动量定理的应用步骤
(1)确定研究对象:一般为单个物体;
(2)明确物理过程:受力分析,求出合外力的冲量;
(3)明确研究对象的初末状态及相应的动量;
(4)选定正方向,确定在物理过程中研究对象的动量的变化;
(5)根据动量定理列方程,统一单位后代入数据求解。
二、动量定理
例5、质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点经历的时间为0.5s,求弹性绳对工人的平均作用力.(g = 10m/s2)
分析:以工人为研究对象,其运动过程分两个阶段:在空中自由下落5m,获得一定速度v ;弹性绳伸直后的运动,先加速后减速到速度为零,到达最低点,经历0.5s .
解法1:分段求解. 由 vt2 = 2gh, 得:v=10m/s
规定竖直向上为正方向,由 I合=Δp
(T – mg) t = mv’ – mv
得: T = mg+ (mv’ – mv)/ t = 500N + [0 – 50×( – 10) ] /0.5 N=1500N
解法2:全程处理.由h = gt 2/2,自由下落5m经受历的时间为:
t 1= 1s
规定竖直向下为正方向,由 I合=Δp
mg (t1 + t2) –Tt2= mv’ – mv=0
得:T = mg (t1 + t2)/ t2 = 50×10×( 1+0.5) /0.5N=1500N
二、动量定理
变题:质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点弹性绳伸长了2m,求弹性绳对工人的平均作用力.(g = 10m/s2)
解:全程处理.由W = ΔEk,
Mg(H+h) – Th = 0–0
T= Mg(H+h) /h = 50×10×( 5+2) /2N =1750N
小结:在题中涉及到的物理量主要是F、s、m、v 时,考虑用动能定理求解.
何时考虑用动能定理求解?
二、动量定理
越长,
一定,
越短,
则F越小.
则F越大.
知识应用:
一定,
为什么跳远时要有沙坑?
为什么跳高时要厚厚的海绵?
三、动量定理应用:解释现象
鸡蛋从一米多高的地方落到地板上,肯定会被打破,但如果在地板上放一块泡沫塑料垫,让鸡蛋落到泡沫塑料上,结果鸡蛋却保持完好无损,为什么?
三、动量定理应用:解释现象
杂技表演时,常可看见有人用铁锤猛击放在“大力士”身上的大石块,石裂而人不伤,这又是为什么?
三、动量定理应用:解释现象
一定,
越长,
则F 越小。
学以致用:
透过现象看本质--缓冲
三、动量定理应用:解释现象
一定,
越长,
一定,
越短,
则F 越小。
则F 越大。
三、动量定理应用
例1、把重物压在纸带上,用一水平力缓缓拉动纸带,重物跟着纸带一起运动;若迅速拉动纸带,纸带就会从重物下抽出,解释这个现象的正确说法是( )
A、在缓缓拉动纸带时,纸带给重物的摩擦力大
B、在迅速拉动纸带时,纸带给重物的摩擦力大
C、在缓缓拉动纸带时,纸带给重物的冲量大
D、在迅速拉动纸带时,纸带给重物的冲量大
BC
F一定时
ΔP = F合Δt
三、动量定理应用:解释现象
例2、玻璃杯从同一高度落下,掉在水泥地上比掉在草地上容易碎,这是由于在玻璃杯与水泥地撞击过程中( )
A、玻璃杯的动量较大 B、玻璃杯受到的冲量较大
C、玻璃杯的动量变化较大 D、玻璃杯的动量变化较快
D
例3、人从高处跳到低处时,为了安全,一般都是让脚尖先着地,这样做是为了( )
A、减小冲量
B、减小动量的变化量
C、增长与地面作用时间,从而减小冲力
D、增大人对地面的压强,起到安全作用
C
三、动量定理应用:解释现象
三、动量定理应用:解释现象
例1:一质点在水平面内以速度v做匀速圆周运动,如图,质点从位置A开始,经1/2圆周,质点所受合力的冲量是多少
vA
A
B
vB
O
解:质点做匀速圆周运动,合力是一个大小不变、但方向不断变化的力,
注意:变力的冲量一般不能直接由F·Δt求出,可借助ΣF·Δt=Δp间接求出,即合外力力的冲量由末动量与初动量的矢量差来决定.
以vB方向为正,因为vA =- v , vB = v ,
则Δp=mvB - mvA =m[v – ( - v )]=2mv,合力冲量与vB同向.
三、动量定理应用:动力学问题
例2:一质量为m的小球,以初速度v0 沿水平方向射出,恰好垂直地射到一倾角为300的固定斜面上,并立即反方向弹回.已知反弹速度的大小是入射速度大小的3/4,求在碰撞中斜面对小球的冲量大小.
解:小球在碰撞斜面前做平抛运动.设刚要碰撞斜面时小球速度为v. 由题意,v 的方向与竖直线的夹角为30°,且水平分量仍为v0,如右图.
v0
30°
v0
v
30°
由此得 v = 2v0 ①
碰撞过程中,小球速度由 v 变为反向的 3v/4,
碰撞时间极短,可不计重力的冲量,
由动量定理,斜面对小球的冲量为
由①、②得
三、动量定理应用:动力学问题
例3、质量为m 的物体作平抛运动,求抛出后第2个t 秒内物体动量的变化.
分析:由动量定理,
Δp = I合= mg t ,方向竖直向下.
已知物体所受的冲量,求动量的变化.
三、动量定理应用:动力学问题
例4、质量为4 kg的物体以2 m/s的初速度做匀变速直线运动,经过2 s,动量大小变为14 kg·m/s,则该物体( )
A.所受合外力的大小可能大于11 N
B.所受合外力的大小可能小于3 N
C.冲量大小可能小于6 N·s
D.冲量大小可能大于18 N·s
若以物体初速度方向为正方向,初动量p1=mv1=8 kg·m/s,则有两种可能末动量:
当p2=14 kg·m/s,则Ft=p2-p1=6 kg·m/s,F=3 N;
当p2=-14 kg·m/s,则Ft=p2-p1=-22 kg·m/s,F=-11 N,
负号表示方向,故选项A、B、C错误,D正确。
D
三、动量定理应用:动力学问题
例5、质量为M 、足够长的小车静止在光滑的水平面上,质量为m 的小物块以初速度v0 从小车的左端滑上小车的上表面.已知物块和小车上表面间的动摩擦因数为μ,求小物块从滑上小车到相对小车静止经历的时间.
f
f ’
v
解:规定向右为正方向,
对m: - μmgt = mv – mv0
对M: μmgt = Mv – 0
联立: t = Mv0 /μg(M+m)
如何求解方程也值得注意
v0
M
m
m
M
三、动量定理应用:动力学问题
例6、人们对手机的依赖性越来越强,有些人喜欢躺着看手机,经常出现手机砸伤眼睛的情况。若手机质量为120g,从离人眼为 20cm 的高度无初速掉落,砸到眼睛后手机反弹的高度为 5cm, 眼睛受到手机的冲击时间约为0.1s,(不计空气阻力,取重力加速度g=10m/s2)。求:
(1) 手机与眼睛作用过程中手机动量变化大小;
(2) 手机对眼睛的平均作用力为多大。
三、动量定理应用:动力学问题
总结解题步骤
1、确定研究对象,确定研究过程。
2、规定正方向,确定始、末两个状态的动量。
3、分析物体的受力情况,确定合外力的冲量。
4、根据动量定理列式求解。
三、动量定理应用:动力学问题
一.知识结构
1.动量、动量变化量和冲量
2.定理及理解 I 方向关系
3. 应用
(1)解释现象
(2)简单计算
一定,
越长,
一定,
越短,
则F越小。
则F越大。
二.我们要有善于观察,勇于探索,不懈追求,精益求精的精神
小结
牛顿第二定律
力的瞬时效果
——产生加速度
动能定理
力对空间的积累
——引起动能改变
动量定理
力对时间的积累
——引起动量改变
总结:从不同的角度看待力的作用的量度
矢量式
标量式
矢量式
牛顿第二定律另一表述:F=Δp/Δt
1、关于冲量、动量及动量变化,下列说法正确的是:
A. 合外力的冲量方向一定和动量变化量的方向相同
B. 合外力冲量的大小一定和动量变化量的大小相同
C. 动量的大小不变,冲量一定为零。
D..动量的变化大,合外力一定大。
巩固自测题
AB
2.从高处跳下,与地面接触时双腿弯曲,这样是为了( )
A、减少落地时的动量
B、减少动量的变化
C、减少冲量
D、减小地面对人的冲力
D
巩固自测题
3.如图质量为m的物体在跟水平方向成Θ角的F作用下,以速度V匀速前进t秒,则物体在这段时间内受到力F的冲量与合外力的冲量各为( )
A. Ft FtcosΘ B. Ftsin Θ Ftcos Θ
C. Ft 0 D. Ft Ftsin Θ
Θ
C
巩固自测题
4.在空间某一点以大小相同的速度分别自由下落、竖直上抛、竖直下抛质量相等的小球,(若空气阻力不计,小球均未落地) 经过t秒: 则( )
(A)作上抛运动的小球动量变化最小
(B)作下抛运动的小球动量变化最小
(C)自由下落小球动量变化最小
(D)三小球动量的变化量相等
D
巩固自测题
第1章 动量守恒定律
第2节 动量和动量定理
船靠岸时边缘上的废旧轮胎
见物思理:下列生活中的现象蕴含了什么奥秘?
摩托车头盔里的衬垫
跳高用的海绵垫
物体碰撞会受到力的作用,物体动量变化和力有什么关系?
汽车的安全气囊
气功表演:碎大石
情景及问题创设:在光滑水平面上的质量为 m 的物体在水平恒力 F 的作用下,经过时间 t,速度由 v 变为 v′ ,如何推导这几个量之间的关系?
可得Ft= mv′ - mv ,即Ft= p′ - p
解:如图所示,物体的初动量为 p= mv,末动量为p′ = mv′ ,
由加速度的定义式:
由牛顿第二定律F = ma = ,
理论推导
4.意义:(1)冲量是矢量,作用力的方向不变时其方向与力的方向相同。
(2 ) 冲量是过程量,反映了力对时间的积累效应。
1.定义:在物理学中,把力与力的作用时间的乘积叫做力的冲量。
2.公式:I=F Δt
3.单位:牛·秒(N·s)
若F为变力,如何求其冲量?
5.变力的冲量:
一、冲量
“面积”””
“冲量”
冲量 功
单位 N·s J
公式 I=F·Δt W=Fl·cosα
标矢 矢量 标量
意义 表示力对时间的累积 表示力对空间的累积
正负 表示冲量的方向 表示动力(阻力)做功
效果 改变物体的动量 改变物体的能量
一、冲量
6.冲量与功的区别
例1:
B
一、冲量
例2.质量为 m 的物体放在水平地面上,在与水平面成 角的拉力F 作用下由静止开始运动,经时间 t 速度达到 v,在这段时间内拉力 F 和重力 mg 冲量大小分别是 ( )
A.Ft,0
B.Ft cos , 0
C.mv, 0
D.Ft, mgt
D
F
v
mg
一、冲量
练习:如图所示,质量为2kg的物体沿倾角为30°高为h=5m的光滑斜面由静止从顶端下滑到底端的过程中 (g=10m/s2) ,求:
(1)重力的冲量;
(2)支持力的冲量;
(3)合外力的冲量.
mg
合外力的冲量IF合=F合·t=mgsin300 t=20N·s.
重力的冲量IG=mg·t=2×10×2N·s=40N·s.
支持力的冲量IF=F·t=mgcos300·t=20 N·s,
一、冲量
例3、A、B两个相同的物体,以相同的初速度分别在粗糙程度不同的水平面上运动,B物体先停下来,A物体又经较长时间停下来,下面的正确描述是( )
A、A物体受到的冲量大
B、B物体受到的冲量大
C、两个物体受到的冲量大小相等
D、这是不可能判断的
C
一、冲量
解:如图所示,物体的初动量为p=mv、末动量为 p、=mv` ,
由加速度的定义式
由牛顿第二定律 F=ma=
可得F t=mv ′ -mv ,即 F t =p ′ -p
1、内容:
2、公式:
Ft=mv'-mv
物体在一个过程中所受力的冲量等于它在这个过程始末的动量变化量.
3、说明:
①公式中的F指的是合外力,可以是恒力,可以是变力.
②公式表明合外力的冲量是动量变化的原因;
③动量定理公式是矢量式,计算时要先规定正方向,遵循平行四边形定则.
④动量定理不仅适用于宏观低速,同样适用于微观高速.
或
(过程量可通过状态量的变化来反映)
合力
末动量
初动量
二、动量定理
二、动量定理
例4、一个质量为0.18kg 的垒球,以25m/s的水平速度飞向球棒,被球棒打击后反向水平飞回,速度大小变为45m/s,设球棒与垒球的作用时间为0.01s。球棒对垒球的平均作用力是多大?
解:沿垒球飞向球棒时的方向建立坐标轴,
垒球的初动量为
p=mv=0.18×25 kg·m/s=4.5kg·m/s
垒球的末动量为
p'=mv'=(-0.18)×25 kg·m/s=-8.1kg·m/s
垒球所受平均作用力大小为1260N,
力的方向与垒球飞来的方向相反
4、动量定理的应用步骤
(1)确定研究对象:一般为单个物体;
(2)明确物理过程:受力分析,求出合外力的冲量;
(3)明确研究对象的初末状态及相应的动量;
(4)选定正方向,确定在物理过程中研究对象的动量的变化;
(5)根据动量定理列方程,统一单位后代入数据求解。
二、动量定理
例5、质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点经历的时间为0.5s,求弹性绳对工人的平均作用力.(g = 10m/s2)
分析:以工人为研究对象,其运动过程分两个阶段:在空中自由下落5m,获得一定速度v ;弹性绳伸直后的运动,先加速后减速到速度为零,到达最低点,经历0.5s .
解法1:分段求解. 由 vt2 = 2gh, 得:v=10m/s
规定竖直向上为正方向,由 I合=Δp
(T – mg) t = mv’ – mv
得: T = mg+ (mv’ – mv)/ t = 500N + [0 – 50×( – 10) ] /0.5 N=1500N
解法2:全程处理.由h = gt 2/2,自由下落5m经受历的时间为:
t 1= 1s
规定竖直向下为正方向,由 I合=Δp
mg (t1 + t2) –Tt2= mv’ – mv=0
得:T = mg (t1 + t2)/ t2 = 50×10×( 1+0.5) /0.5N=1500N
二、动量定理
变题:质量为50kg 的工人,身上系着长为5m的弹性安全带在高空作业,不慎掉下,若从弹性绳开始伸直到工人落到最低点弹性绳伸长了2m,求弹性绳对工人的平均作用力.(g = 10m/s2)
解:全程处理.由W = ΔEk,
Mg(H+h) – Th = 0–0
T= Mg(H+h) /h = 50×10×( 5+2) /2N =1750N
小结:在题中涉及到的物理量主要是F、s、m、v 时,考虑用动能定理求解.
何时考虑用动能定理求解?
二、动量定理
越长,
一定,
越短,
则F越小.
则F越大.
知识应用:
一定,
为什么跳远时要有沙坑?
为什么跳高时要厚厚的海绵?
三、动量定理应用:解释现象
鸡蛋从一米多高的地方落到地板上,肯定会被打破,但如果在地板上放一块泡沫塑料垫,让鸡蛋落到泡沫塑料上,结果鸡蛋却保持完好无损,为什么?
三、动量定理应用:解释现象
杂技表演时,常可看见有人用铁锤猛击放在“大力士”身上的大石块,石裂而人不伤,这又是为什么?
三、动量定理应用:解释现象
一定,
越长,
则F 越小。
学以致用:
透过现象看本质--缓冲
三、动量定理应用:解释现象
一定,
越长,
一定,
越短,
则F 越小。
则F 越大。
三、动量定理应用
例1、把重物压在纸带上,用一水平力缓缓拉动纸带,重物跟着纸带一起运动;若迅速拉动纸带,纸带就会从重物下抽出,解释这个现象的正确说法是( )
A、在缓缓拉动纸带时,纸带给重物的摩擦力大
B、在迅速拉动纸带时,纸带给重物的摩擦力大
C、在缓缓拉动纸带时,纸带给重物的冲量大
D、在迅速拉动纸带时,纸带给重物的冲量大
BC
F一定时
ΔP = F合Δt
三、动量定理应用:解释现象
例2、玻璃杯从同一高度落下,掉在水泥地上比掉在草地上容易碎,这是由于在玻璃杯与水泥地撞击过程中( )
A、玻璃杯的动量较大 B、玻璃杯受到的冲量较大
C、玻璃杯的动量变化较大 D、玻璃杯的动量变化较快
D
例3、人从高处跳到低处时,为了安全,一般都是让脚尖先着地,这样做是为了( )
A、减小冲量
B、减小动量的变化量
C、增长与地面作用时间,从而减小冲力
D、增大人对地面的压强,起到安全作用
C
三、动量定理应用:解释现象
三、动量定理应用:解释现象
例1:一质点在水平面内以速度v做匀速圆周运动,如图,质点从位置A开始,经1/2圆周,质点所受合力的冲量是多少
vA
A
B
vB
O
解:质点做匀速圆周运动,合力是一个大小不变、但方向不断变化的力,
注意:变力的冲量一般不能直接由F·Δt求出,可借助ΣF·Δt=Δp间接求出,即合外力力的冲量由末动量与初动量的矢量差来决定.
以vB方向为正,因为vA =- v , vB = v ,
则Δp=mvB - mvA =m[v – ( - v )]=2mv,合力冲量与vB同向.
三、动量定理应用:动力学问题
例2:一质量为m的小球,以初速度v0 沿水平方向射出,恰好垂直地射到一倾角为300的固定斜面上,并立即反方向弹回.已知反弹速度的大小是入射速度大小的3/4,求在碰撞中斜面对小球的冲量大小.
解:小球在碰撞斜面前做平抛运动.设刚要碰撞斜面时小球速度为v. 由题意,v 的方向与竖直线的夹角为30°,且水平分量仍为v0,如右图.
v0
30°
v0
v
30°
由此得 v = 2v0 ①
碰撞过程中,小球速度由 v 变为反向的 3v/4,
碰撞时间极短,可不计重力的冲量,
由动量定理,斜面对小球的冲量为
由①、②得
三、动量定理应用:动力学问题
例3、质量为m 的物体作平抛运动,求抛出后第2个t 秒内物体动量的变化.
分析:由动量定理,
Δp = I合= mg t ,方向竖直向下.
已知物体所受的冲量,求动量的变化.
三、动量定理应用:动力学问题
例4、质量为4 kg的物体以2 m/s的初速度做匀变速直线运动,经过2 s,动量大小变为14 kg·m/s,则该物体( )
A.所受合外力的大小可能大于11 N
B.所受合外力的大小可能小于3 N
C.冲量大小可能小于6 N·s
D.冲量大小可能大于18 N·s
若以物体初速度方向为正方向,初动量p1=mv1=8 kg·m/s,则有两种可能末动量:
当p2=14 kg·m/s,则Ft=p2-p1=6 kg·m/s,F=3 N;
当p2=-14 kg·m/s,则Ft=p2-p1=-22 kg·m/s,F=-11 N,
负号表示方向,故选项A、B、C错误,D正确。
D
三、动量定理应用:动力学问题
例5、质量为M 、足够长的小车静止在光滑的水平面上,质量为m 的小物块以初速度v0 从小车的左端滑上小车的上表面.已知物块和小车上表面间的动摩擦因数为μ,求小物块从滑上小车到相对小车静止经历的时间.
f
f ’
v
解:规定向右为正方向,
对m: - μmgt = mv – mv0
对M: μmgt = Mv – 0
联立: t = Mv0 /μg(M+m)
如何求解方程也值得注意
v0
M
m
m
M
三、动量定理应用:动力学问题
例6、人们对手机的依赖性越来越强,有些人喜欢躺着看手机,经常出现手机砸伤眼睛的情况。若手机质量为120g,从离人眼为 20cm 的高度无初速掉落,砸到眼睛后手机反弹的高度为 5cm, 眼睛受到手机的冲击时间约为0.1s,(不计空气阻力,取重力加速度g=10m/s2)。求:
(1) 手机与眼睛作用过程中手机动量变化大小;
(2) 手机对眼睛的平均作用力为多大。
三、动量定理应用:动力学问题
总结解题步骤
1、确定研究对象,确定研究过程。
2、规定正方向,确定始、末两个状态的动量。
3、分析物体的受力情况,确定合外力的冲量。
4、根据动量定理列式求解。
三、动量定理应用:动力学问题
一.知识结构
1.动量、动量变化量和冲量
2.定理及理解 I 方向关系
3. 应用
(1)解释现象
(2)简单计算
一定,
越长,
一定,
越短,
则F越小。
则F越大。
二.我们要有善于观察,勇于探索,不懈追求,精益求精的精神
小结
牛顿第二定律
力的瞬时效果
——产生加速度
动能定理
力对空间的积累
——引起动能改变
动量定理
力对时间的积累
——引起动量改变
总结:从不同的角度看待力的作用的量度
矢量式
标量式
矢量式
牛顿第二定律另一表述:F=Δp/Δt
1、关于冲量、动量及动量变化,下列说法正确的是:
A. 合外力的冲量方向一定和动量变化量的方向相同
B. 合外力冲量的大小一定和动量变化量的大小相同
C. 动量的大小不变,冲量一定为零。
D..动量的变化大,合外力一定大。
巩固自测题
AB
2.从高处跳下,与地面接触时双腿弯曲,这样是为了( )
A、减少落地时的动量
B、减少动量的变化
C、减少冲量
D、减小地面对人的冲力
D
巩固自测题
3.如图质量为m的物体在跟水平方向成Θ角的F作用下,以速度V匀速前进t秒,则物体在这段时间内受到力F的冲量与合外力的冲量各为( )
A. Ft FtcosΘ B. Ftsin Θ Ftcos Θ
C. Ft 0 D. Ft Ftsin Θ
Θ
C
巩固自测题
4.在空间某一点以大小相同的速度分别自由下落、竖直上抛、竖直下抛质量相等的小球,(若空气阻力不计,小球均未落地) 经过t秒: 则( )
(A)作上抛运动的小球动量变化最小
(B)作下抛运动的小球动量变化最小
(C)自由下落小球动量变化最小
(D)三小球动量的变化量相等
D
巩固自测题
