人教版八年级上册 15.2.3整数指数幂 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级上册 15.2.3整数指数幂 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 21:28:00 | ||
图片预览




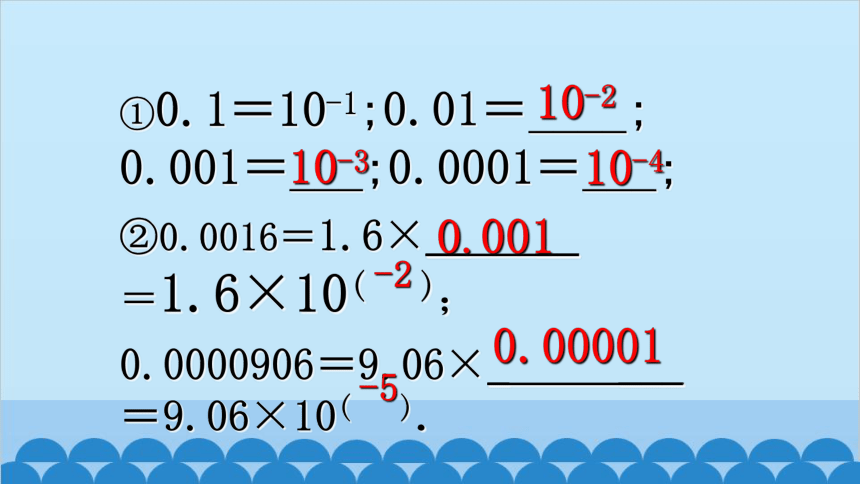

文档简介
(共20张PPT)
1.情景导入
人教版·八年级数学·上册
15.2.3 整数指数幂
阅读P142-145页,思考:
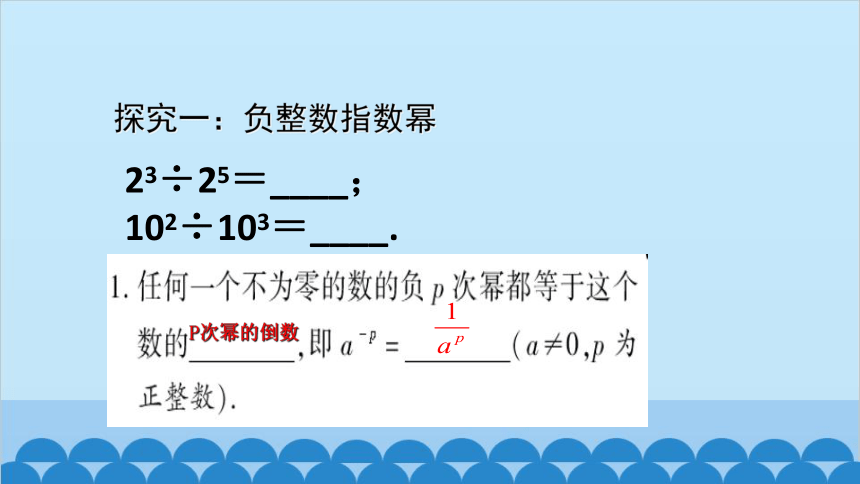
23÷25=____;
102÷103=____.
探究一:负整数指数幂
P次幂的倒数
整数指数幂的性质
①0.1=10-1;0.01=____;
0.001=___;0.0001=___;
②0.0016=1.6×__ __
=1.6×10( );
0.0000906=9.06×_ ___
=9.06×10( ).
10-2
10-4
10-3
0.00001
0.001
-2
-5
10
1
(1)原式=3.5×10-5
解:
(2)原式=-6.08×10-3
(3)原式=1.39×106
4:计算,把结果化为正整数指数幂
(x5y-3)4;
解:
a5b-3·(a-2b2)3.
5:把下列各式转化为只含正整数指数幂的形式.
解:
7:用科学记数法表示下列各数.
①0.0026;②-0.0000301;③1390000.
解:
①0.0026=2.6×10-3;
②-0.0000301=-3.01×10-5;
③1390000=1.39×106.
下列是用科学记数法表示的数,写出原来的数.
(1)2×10-8 (2)7.001×10-6
(1)0.000 000 02 (2)0.000 007 001
本课时我们学习了哪些知识?
1.零指数幂:当a≠0时,a0=1.
2.负整数指数幂:当n是正整数时,a-n=
3.整数指数幂的运算性质:
(1)am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
一、整数指数幂
课堂小结
二.用科学记数法表示绝对值小于1的数
绝对值小于1的数用科学记数法表示为a×10-n的形式,1≤│a│ <10,n为原数第1个不为0的数字前面所有0的个数(包括小数点前面那个0).
2:把下列各式转化为只含正整数指数幂的形式.
解:
解:
(1)(2a2b)-2·(a-1b-2)-3
解:
3.化简:
1.情景导入
人教版·八年级数学·上册
15.2.3 整数指数幂
阅读P142-145页,思考:
23÷25=____;
102÷103=____.
探究一:负整数指数幂
P次幂的倒数
整数指数幂的性质
①0.1=10-1;0.01=____;
0.001=___;0.0001=___;
②0.0016=1.6×__ __
=1.6×10( );
0.0000906=9.06×_ ___
=9.06×10( ).
10-2
10-4
10-3
0.00001
0.001
-2
-5
10
1
(1)原式=3.5×10-5
解:
(2)原式=-6.08×10-3
(3)原式=1.39×106
4:计算,把结果化为正整数指数幂
(x5y-3)4;
解:
a5b-3·(a-2b2)3.
5:把下列各式转化为只含正整数指数幂的形式.
解:
7:用科学记数法表示下列各数.
①0.0026;②-0.0000301;③1390000.
解:
①0.0026=2.6×10-3;
②-0.0000301=-3.01×10-5;
③1390000=1.39×106.
下列是用科学记数法表示的数,写出原来的数.
(1)2×10-8 (2)7.001×10-6
(1)0.000 000 02 (2)0.000 007 001
本课时我们学习了哪些知识?
1.零指数幂:当a≠0时,a0=1.
2.负整数指数幂:当n是正整数时,a-n=
3.整数指数幂的运算性质:
(1)am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
一、整数指数幂
课堂小结
二.用科学记数法表示绝对值小于1的数
绝对值小于1的数用科学记数法表示为a×10-n的形式,1≤│a│ <10,n为原数第1个不为0的数字前面所有0的个数(包括小数点前面那个0).
2:把下列各式转化为只含正整数指数幂的形式.
解:
解:
(1)(2a2b)-2·(a-1b-2)-3
解:
3.化简:
