人教版八年级上册 12.2 三角形全等的判定ASA(AAS)(第3课时) 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级上册 12.2 三角形全等的判定ASA(AAS)(第3课时) 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 539.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 08:11:53 | ||
图片预览





文档简介
(共21张PPT)
(1)判断三角形全等至少要有几个条件?
至少要有三个条件
(2)我们已学了哪些判定公理?
SSS公理和SAS公理
回顾和思考
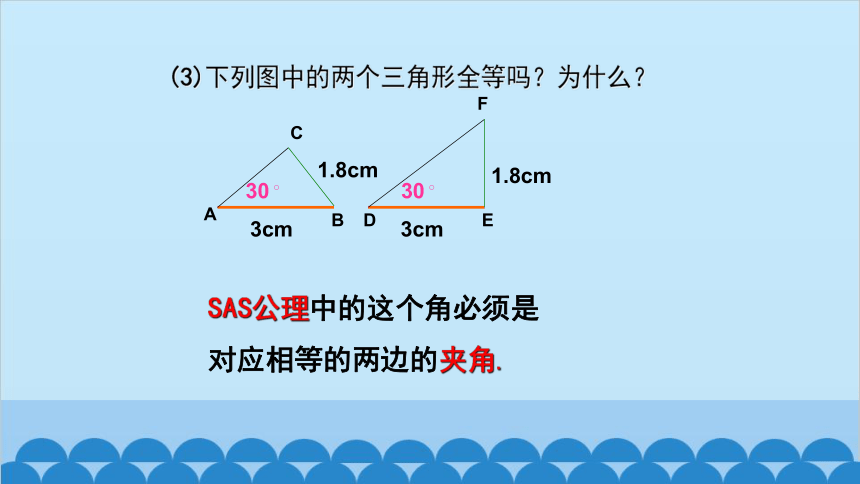
(3)下列图中的两个三角形全等吗?为什么?
3cm
3cm
30
30
A
D
B
E
C
F
1.8cm
1.8cm
SAS公理中的这个角必须是
对应相等的两边的夹角.
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
12.2三角形全等的判定
(ASA和AAS)
先任意画一个△ABC,再画一个△DEF,使DE=AB ,∠D=∠A ,∠E =∠B ,
画好的△DEF能否与原来的三角形重合,由此你能得出什么结论?
探究4
自学课本40-41页练习题上面的部分,思考:
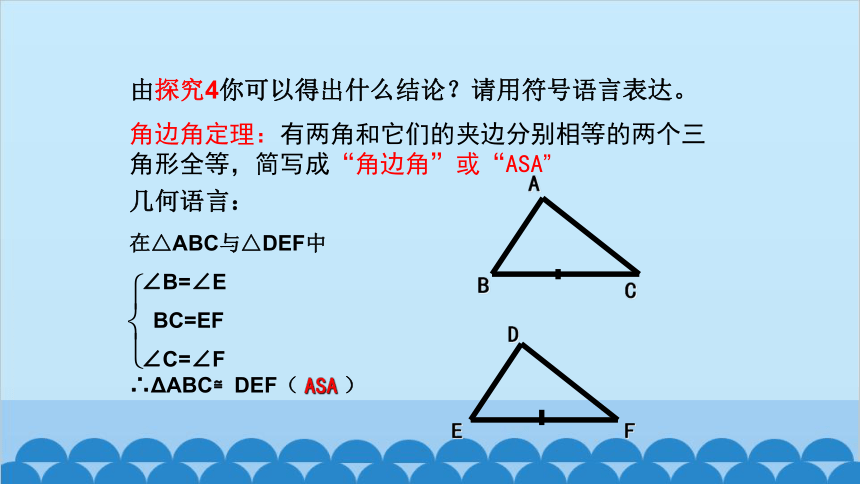
1、由探究4你可以得出什么结论?请用符号语言表达。
2、例3、例4你能理解吗?从例4可以得出什么结论?请用符号语言表达。
3、测量三角尺的内外两个三角形的三个角,由此你认为三个角对应相等的两个三角形全等吗?
4、现在你能解决引入部分的问题吗
在△ABC与△DEF中
∠B=∠E
BC=EF
∠C=∠F ∴ΔABC≌DEF( ASA )
角边角定理:有两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
几何语言:
A
B
C
D
E
F
由探究4你可以得出什么结论?请用符号语言表达。
40页例3、例4你能理解吗?从例4可以得出什么结论?请用符号语言表达。
几何语言:
在△ABC与△DEF中
∠B=∠E,
∠C=∠F ,
AC=DF
∴ΔABC≌DEF( AAS )
角角边定理:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”
A
B
C
D
E
F
3、测量三角尺的内外两个三角形的三个角,由此你认为三个角对应相等的两个三角形全等吗?
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
根据ASA公理,已知三角形的两个角和它们的夹边就能作出这个三角形.
问题 解决
1.如图,已知∠ACB=∠DFE,BC=EF,则应补充一个直接条件 --------------------------,就能使△ABC≌△DEF。
A
B
C
D
E
F
⑴ ∠B=∠E(ASA)
⑵ ∠A=∠D(AAS)
⑶ AC=DF(SAS)
当堂练习
2、 如图,O是AB的中点, = ,
与 全等吗 为什么?
解:
3、 图中的两个三角形全等吗 请说明理由。
A
B
C
D
4、已知 和 中, = ,AB=AC.
求证: (1)
(3) BD=CE
证明:
(2) AE=AD
(全等三角形对应边相等)
又QAB=AC
,
ACD
ABE
D
D
Q
中
和
在
(已知)
(已知)
(公共角)
(等式的性质)
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
要学会用分类的思想数形结合思想,转化的思想解决问题。
小结
当堂检测
1.如图:AB⊥BC上,AD ⊥ DC 垂足分别为B,D,
∠1= ∠ 2。求证 :AB= AD
2.如图:要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长。为什么?
(1)判断三角形全等至少要有几个条件?
至少要有三个条件
(2)我们已学了哪些判定公理?
SSS公理和SAS公理
回顾和思考
(3)下列图中的两个三角形全等吗?为什么?
3cm
3cm
30
30
A
D
B
E
C
F
1.8cm
1.8cm
SAS公理中的这个角必须是
对应相等的两边的夹角.
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
12.2三角形全等的判定
(ASA和AAS)
先任意画一个△ABC,再画一个△DEF,使DE=AB ,∠D=∠A ,∠E =∠B ,
画好的△DEF能否与原来的三角形重合,由此你能得出什么结论?
探究4
自学课本40-41页练习题上面的部分,思考:
1、由探究4你可以得出什么结论?请用符号语言表达。
2、例3、例4你能理解吗?从例4可以得出什么结论?请用符号语言表达。
3、测量三角尺的内外两个三角形的三个角,由此你认为三个角对应相等的两个三角形全等吗?
4、现在你能解决引入部分的问题吗
在△ABC与△DEF中
∠B=∠E
BC=EF
∠C=∠F ∴ΔABC≌DEF( ASA )
角边角定理:有两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
几何语言:
A
B
C
D
E
F
由探究4你可以得出什么结论?请用符号语言表达。
40页例3、例4你能理解吗?从例4可以得出什么结论?请用符号语言表达。
几何语言:
在△ABC与△DEF中
∠B=∠E,
∠C=∠F ,
AC=DF
∴ΔABC≌DEF( AAS )
角角边定理:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“AAS”
A
B
C
D
E
F
3、测量三角尺的内外两个三角形的三个角,由此你认为三个角对应相等的两个三角形全等吗?
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适 你能说明其中理由吗
根据ASA公理,已知三角形的两个角和它们的夹边就能作出这个三角形.
问题 解决
1.如图,已知∠ACB=∠DFE,BC=EF,则应补充一个直接条件 --------------------------,就能使△ABC≌△DEF。
A
B
C
D
E
F
⑴ ∠B=∠E(ASA)
⑵ ∠A=∠D(AAS)
⑶ AC=DF(SAS)
当堂练习
2、 如图,O是AB的中点, = ,
与 全等吗 为什么?
解:
3、 图中的两个三角形全等吗 请说明理由。
A
B
C
D
4、已知 和 中, = ,AB=AC.
求证: (1)
(3) BD=CE
证明:
(2) AE=AD
(全等三角形对应边相等)
又QAB=AC
,
ACD
ABE
D
D
Q
中
和
在
(已知)
(已知)
(公共角)
(等式的性质)
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
要学会用分类的思想数形结合思想,转化的思想解决问题。
小结
当堂检测
1.如图:AB⊥BC上,AD ⊥ DC 垂足分别为B,D,
∠1= ∠ 2。求证 :AB= AD
2.如图:要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长。为什么?
