人教版数学九年级上册23.2.1 中心对称课件 (共18张PPT)
文档属性
| 名称 | 人教版数学九年级上册23.2.1 中心对称课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 520.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 08:24:20 | ||
图片预览

文档简介
(共18张PPT)
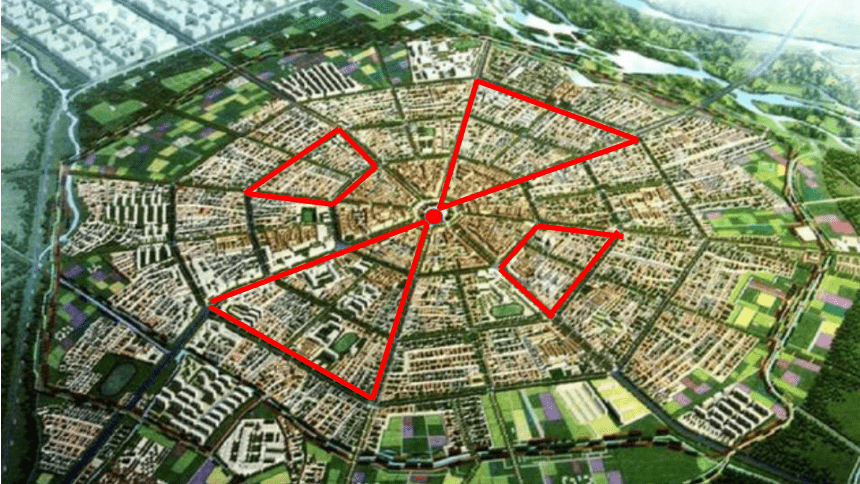
二十三章 旋转
23.2.1 中心对称——中心对称的概念及性质(1)
A
B
C
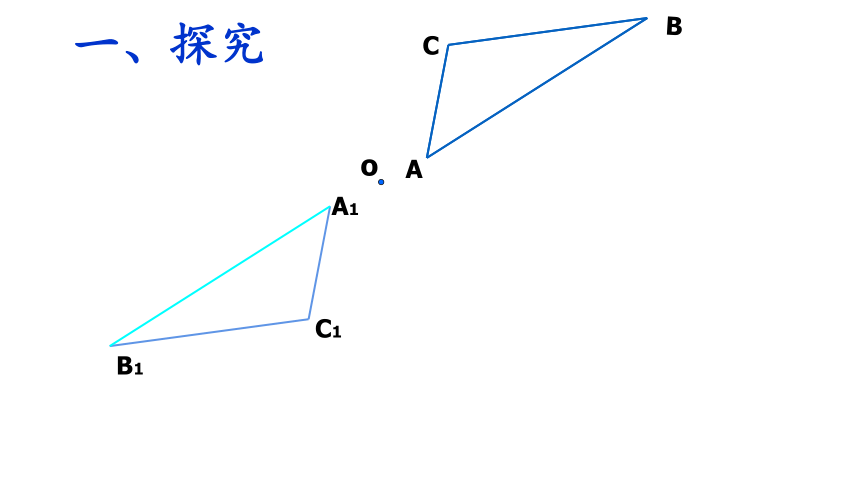
一、探究
A1
B1
C1
o
定义—— 像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
思考: A、O、A1三点的位置关系怎样
线段AO,A1O的大小关系呢
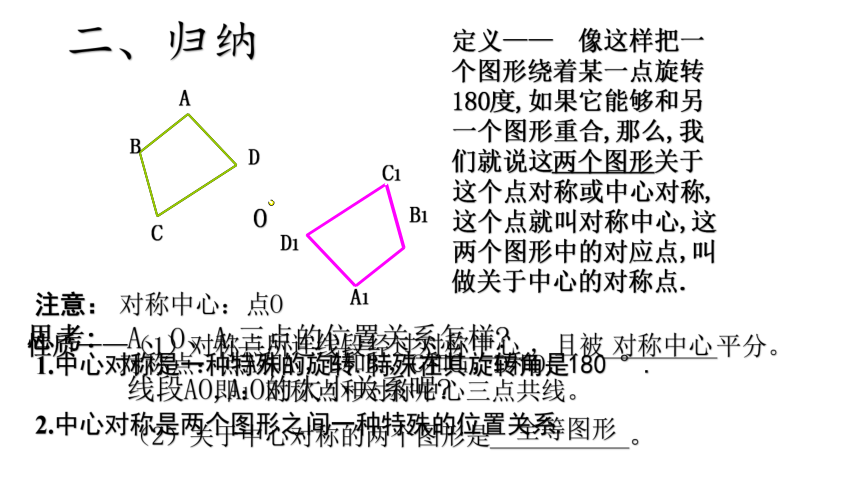
二、归纳
A
B
A1
D1
C1
B1
C
D
O
性质——(1)对称点所连线段经过_________,且被_________平分。
即:对称点和对称中心三点共线。
(2)关于中心对称的两个图形是___________。
对称中心:点O
对称点:点A和A1,B和B1,C和C1,D和D1
对称中心
对称中心
全等图形
注意:
1.中心对称是一种特殊的旋转.特殊在其旋转角是180 °.
2.中心对称是两个图形之间一种特殊的位置关系.
A′
A
O
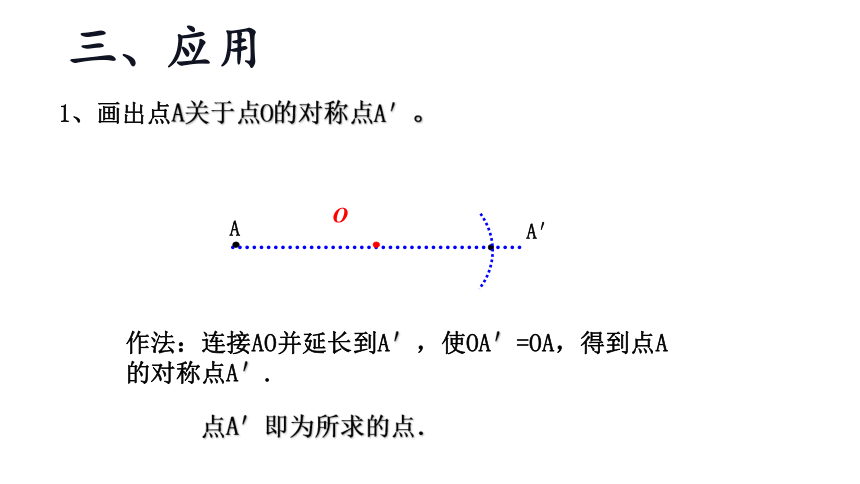
1、画出点A关于点O的对称点A′。
点A′即为所求的点.
作法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.
三、应用
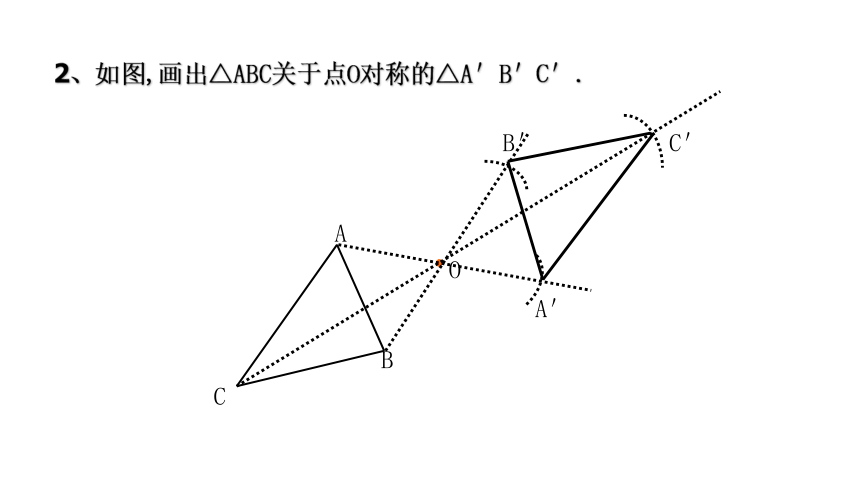
2、如图,画出△ABC关于点O对称的△A′B′C′.
A
B
O
C
A'
B'
C'
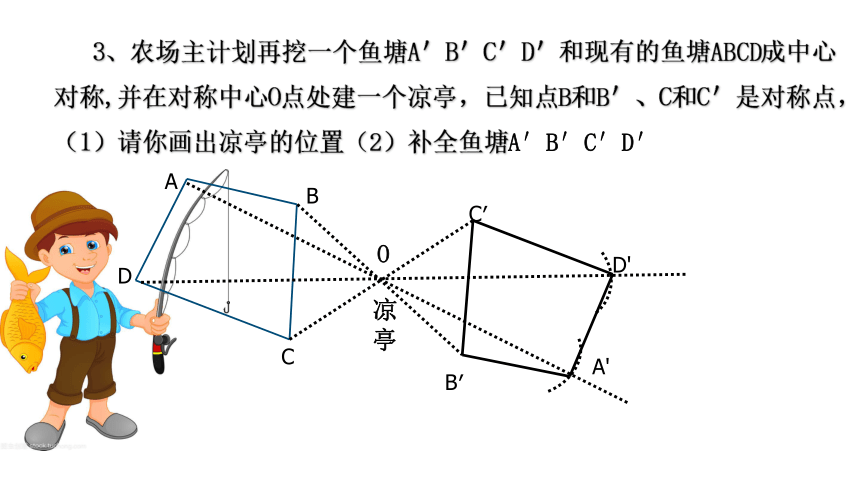
3、农场主计划再挖一个鱼塘A'B'C'D'和现有的鱼塘ABCD成中心对称,并在对称中心O点处建一个凉亭,已知点B和B'、C和C'是对称点,(1)请你画出凉亭的位置(2)补全鱼塘A′B′C′D′
A
B
C
D
C′
B′
O
凉亭
D'
A'
数学来源于生活,
也服务于生活
中心对称
概念
旋转角是180°
性质
1.对称中心与两对称点三点共线;
2.成中心对称的两个图形是全等形
作图
应用1:作中心对称图形;
应用2:找出对称中心.
四、课堂小结
二十三章 旋转
23.2.1 中心对称——中心对称的概念及性质(2)
魔术时间
桌上有四张牌,将其中一张牌旋转180度后,你很快能猜出是哪一张与原来的一模一样吗?
探究中心对称图形的概念
一
(1)线段
(2)平行四边形
A
B
问题:将下面的图形绕O点旋转,你有什么发现?
O
O
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
O
B
A
C
D
中心对称图形的定义
归纳总结
中心对称图形是指一个图形.
注意
探究中心对称图形的性质
二
探究与归纳
A
B
D
C
O
(1)中心对称图形的对称点连线都经过________
(2)中心对称图形的对称点连线被____________
对称中心
对称中心平分
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
归纳
√
√
(1)
(2)
(3)
√
(4)
判一判:下列图形中哪些是中心对称图形?
×
图(1)
图(2)
解密魔术
请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 .
一石激起千层浪
①
汽车方向盘
②
铜钱
③
①
②
③
①
③
谢谢聆听
二十三章 旋转
23.2.1 中心对称——中心对称的概念及性质(1)
A
B
C
一、探究
A1
B1
C1
o
定义—— 像这样把一个图形绕着某一点旋转180度,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称,这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
思考: A、O、A1三点的位置关系怎样
线段AO,A1O的大小关系呢
二、归纳
A
B
A1
D1
C1
B1
C
D
O
性质——(1)对称点所连线段经过_________,且被_________平分。
即:对称点和对称中心三点共线。
(2)关于中心对称的两个图形是___________。
对称中心:点O
对称点:点A和A1,B和B1,C和C1,D和D1
对称中心
对称中心
全等图形
注意:
1.中心对称是一种特殊的旋转.特殊在其旋转角是180 °.
2.中心对称是两个图形之间一种特殊的位置关系.
A′
A
O
1、画出点A关于点O的对称点A′。
点A′即为所求的点.
作法:连接AO并延长到A′,使OA′=OA,得到点A的对称点A′.
三、应用
2、如图,画出△ABC关于点O对称的△A′B′C′.
A
B
O
C
A'
B'
C'
3、农场主计划再挖一个鱼塘A'B'C'D'和现有的鱼塘ABCD成中心对称,并在对称中心O点处建一个凉亭,已知点B和B'、C和C'是对称点,(1)请你画出凉亭的位置(2)补全鱼塘A′B′C′D′
A
B
C
D
C′
B′
O
凉亭
D'
A'
数学来源于生活,
也服务于生活
中心对称
概念
旋转角是180°
性质
1.对称中心与两对称点三点共线;
2.成中心对称的两个图形是全等形
作图
应用1:作中心对称图形;
应用2:找出对称中心.
四、课堂小结
二十三章 旋转
23.2.1 中心对称——中心对称的概念及性质(2)
魔术时间
桌上有四张牌,将其中一张牌旋转180度后,你很快能猜出是哪一张与原来的一模一样吗?
探究中心对称图形的概念
一
(1)线段
(2)平行四边形
A
B
问题:将下面的图形绕O点旋转,你有什么发现?
O
O
共同点:
(1)都绕一点旋转了180度;
(2)都与原图形完全重合.
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
O
B
A
C
D
中心对称图形的定义
归纳总结
中心对称图形是指一个图形.
注意
探究中心对称图形的性质
二
探究与归纳
A
B
D
C
O
(1)中心对称图形的对称点连线都经过________
(2)中心对称图形的对称点连线被____________
对称中心
对称中心平分
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
归纳
√
√
(1)
(2)
(3)
√
(4)
判一判:下列图形中哪些是中心对称图形?
×
图(1)
图(2)
解密魔术
请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 .
一石激起千层浪
①
汽车方向盘
②
铜钱
③
①
②
③
①
③
谢谢聆听
同课章节目录
