新课标苏教版六上4.2《解决问题的策略(2)》课件(34张ppt)
文档属性
| 名称 | 新课标苏教版六上4.2《解决问题的策略(2)》课件(34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 13:51:40 | ||
图片预览







文档简介
(共34张PPT)
解决问题的策略(2)
苏教版六年级上册
教学目标
1.学习目标描述:学会用“假设”的策略理解题意、分析数量关系,并能根据问题的特点确定合理的解题步骤。
2.学习内容分析:本课时是用策略解决问题的第二课时,在第一课时里尝试了用替换的策略解决问题的方法,这节课是在进一步感受用策略解决问题的思路和步骤这一思考方法,从而生成和进一步巩固“假设”策略这一思考方法。
教学目标
3.学科核心素养分析:使学生在对解决实际问题过程的不断反思中,感受“假设”策略对于解决特定问题的价值,进一步发展分析、综合和简单推理能力;进一步积累解决问题的经验,增强解决问题的策略意识,获得解决问题的成功体验,提高学好数学的信心。
新知导入
在1个大盒和4个同样的小盒里装满球,正好是90个。如果2个小盒与1个大盒装的一样多,那么大盒里装了多少个球?每个小盒呢?
怎样理解题中数量之间的关系?
1个大盒+4个小盒=90个
2个小盒=1个大盒
你准备怎样解决这个问题呢?与同伴说说自己的想法。
新知导入
在1个大盒和4个同样的小盒里装满球,正好是90个。如果2个小盒与1个大盒装的一样多,那么大盒里装了多少个球?每个小盒呢?
假设把球都装入小盒。
1个大盒+4个小盒=90个
2个小盒
90÷(4÷2+1)=30(个)
答:每个大盒里装了30个球,每个小盒里装了15个球。
30÷2=15(个)
新知导入
在1个大盒和4个同样的小盒里装满球,正好是90个。如果2个小盒与1个大盒装的一样多,那么大盒里装了多少个球?每个小盒呢?
假设把球都装入大盒。
1个大盒+4个小盒=90个
2个大盒
90÷(2+4)=15(个)
答:每个大盒里装了30个球,每个小盒里装了15个球。
15×2=30(个)
新知导入
通过假设替换,可以转化问题,使数量关系变得简单。
如果把上题中的已知条件稍微改一下,又该怎样解答呢?
新知讲解
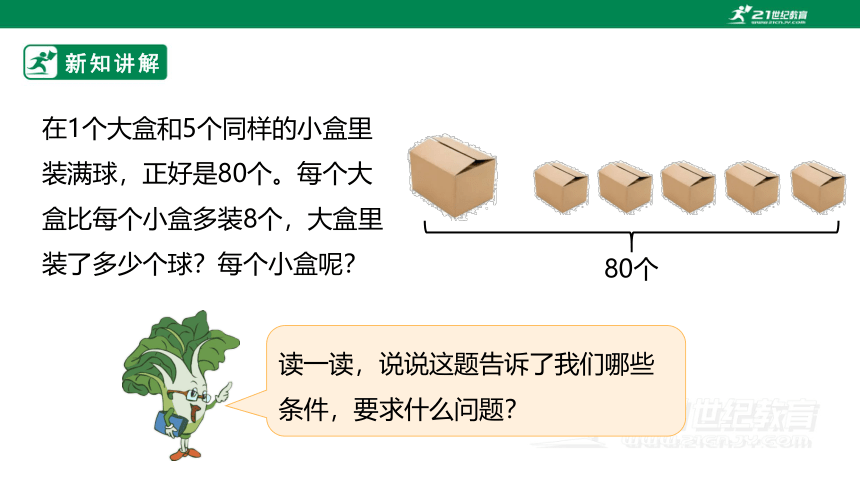
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
80个
读一读,说说这题告诉了我们哪些条件,要求什么问题?
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
怎样理解题意中的数量关系呢?
1个大盒里的球的个数+5个小盒里球的个数=80
1个大盒里球的个数-8=1个小盒里球的个数
1个小盒里球的个数+8=1个大盒里球的个数
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
合作提示:
你能根据假设后的数量关系想想怎样解决这个问题?并与小组学生交流自己的想法。
新知讲解
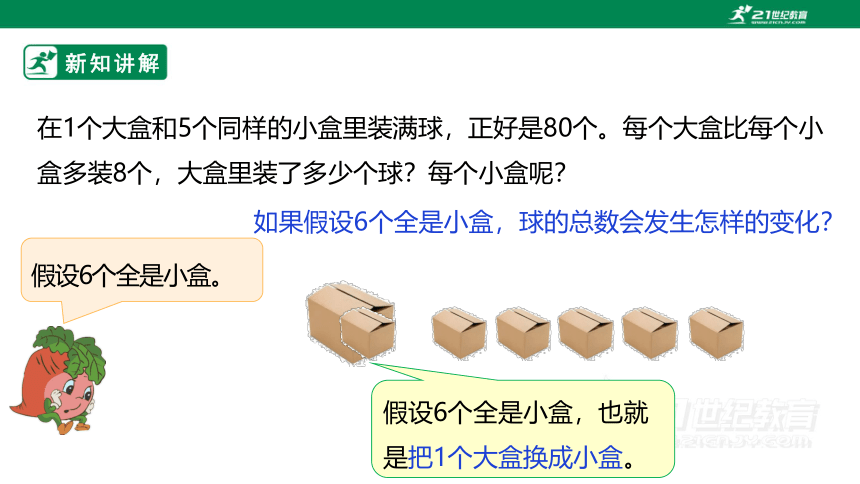
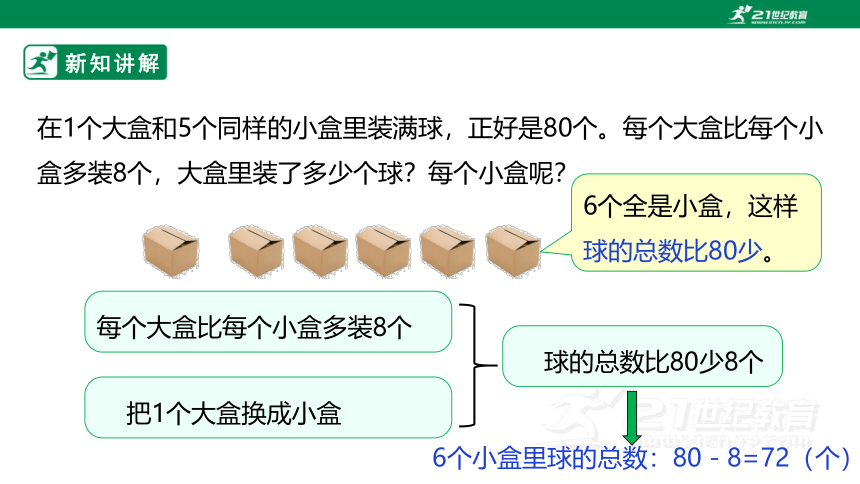
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
假设6个全是小盒。
如果假设6个全是小盒,球的总数会发生怎样的变化?
假设6个全是小盒,也就是把1个大盒换成小盒。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
每个大盒比每个小盒多装8个
6个全是小盒,这样球的总数比80少。
把1个大盒换成小盒
球的总数比80少8个
6个小盒里球的总数:80-8=72(个)
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
6个小盒里球的总数:80-8=72(个)
每个小盒里装:72÷6=12(个)
每个大盒里装:12+8=20(个)
检验:20+12×5=80(个)
答:大盒里装了20个,每个小盒装12个。
结合题意,检验一下答案是否正确。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
还可以假设6个全是大盒。
如果假设6个全是大盒,球的总数会发生怎样的变化?
6个全是大盒,球的总数比80多。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
每个大盒比每个小盒多装8个。
把5个小盒换成大盒,球的总数比80多8×5=40(个)。
6个大盒里球的总数是:80+40=120(个)
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
6个大盒里球的总数是:80+40=120(个)
每个大盒里装:120÷6=20(个)
每个小盒里装:20-8=12(个)
检验:20+12×5=80(个)
答:大盒里装了20个,每个小盒装12个。
算出每个大盒里装了多少个球?每个小盒呢?并检验。
新知讲解
刚才我们用两种思路解决了上面的问题,假设6个全是小盒或者假设6个全是大盒,虽然假设的方法不一样,但你发现它们有什么相同的地方?
都是先提出假设。
假设后球的总数与实际数量不一样,这时就需要调整,从而推算出正确的结果。
新知讲解
在进行调整时,我们又是怎么想的?
先算出假设与实际总数相差多少,再算一算每一份相差多少,最后算出调整的数量。
新知讲解
利用“假设”的策略解决相差关系的问题时,先根据解题的需要对已知条件作出假设,通过假设引出差量,然后分析产生差量的原因,找到差量对应的数量来解决问题。
新知讲解
上节课我们学习了例1,明确了假设的策略,今天又学习了例2,用假设的策略解决了另一类比较复杂的问题。回顾例1和例2解决问题的过程,你有什么体会?
都可以通过假设使数量关系变得简单。
要弄清假设前后的数量关系,注意假设前后总量有没有变化。
要在不同的假设方法中选择比较简单的。
课堂练习
1.填一填。
妈妈用96元钱买了6千克苹果和4千克橘子,如果每千克橘子比每千克苹果便宜1.5元。
(1)假设这10千克全买苹果,就必须( )(填“多”或“少”)付( )元,共付( )元,每千克苹果( )元;
(2)假设这10千克全买橘子,就必须( )(填“多”或“少”)付( )元,共付( )元,每千克橘子( )元。
多
6
102
10.2
少
9
87
8.7
课堂练习
2.有 200 位来宾,坐满了12张圆桌和10张方桌,每张圆桌比每张方桌多坐2人,每张圆桌坐多少人?
假设全坐的是圆桌,把10张方桌换成圆桌,总人数比200多10×2=20(人)。
12张圆桌可坐人数:200+10×2=220(人)
每张圆桌:220÷(12+10)=10(人)
答:每张圆桌坐10人。
课堂练习
2.有 200 位来宾,坐满了12张圆桌和10张方桌,每张圆桌比每张方桌多坐2人,每张圆桌坐多少人?
假设全坐的是方桌,把12张圆桌换成方桌,总人数比200少12×2=24(人)。
12张方桌可坐人数:200-12×2=176(人)
每张方桌:176÷(12+10)=8(人)
每张圆桌:8+2=10(人)
答:每张圆桌坐10人。
课堂练习
3.在3个同样的大盒和4个同样的小盒里装满球,正好是120个。每个大盒比每个小盒多装5个,每个大盒和每个小盒里各装了多少个球?
假设假设7个全是大盒,把4个小盒换成大盒,总数比120多5×4=20(个)。
7个大盒里球的总数:120+5×4=140(个)
每个大盒里装:140÷(3+4)=20(个)
每个小盒里装:20-5=15(个)
答:每个大盒里装20个,每个小盒里装15个。
课堂练习
3.在3个同样的大盒和4个同样的小盒里装满球,正好是120个。每个大盒比每个小盒多装5个,每个大盒和每个小盒里各装了多少个球?
假设假设7个全是小盒,把3个大盒换成小盒,总数比120少5×3=15(个)。
7个小盒里球的总数:120-5×3=105(个)
每个小盒里装:105÷(3+4)=15(个)
每个大盒里装:15+5=20(个)
答:每个大盒里装20个,每个小盒里装15个。
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
思考:鸡和兔一共有20只,一共有50条腿。假设20只全是鸡,一共有( )条腿,这样就会减少( )条腿,这是因为把一只兔看作一只鸡就会减少( )条腿,从而可知兔有( )只,鸡有( )只。
40
10
2
5
15
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
假设20只全是鸡。
20只鸡总腿数:2×20=40(条)
假设后腿减少:50-40=10(条)
把一只兔看作一只鸡就会减少:4-2=2(条)
兔:10÷2=5(只)
鸡:20-5=15(只)
答:鸡有15只,兔有5只。
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
思考:鸡和兔一共有20只,一共有50条腿。假设20只全是兔,一共有( )条腿,这样就会增加( )条腿,这是因为把一只鸡看作一只兔就会增加( )条腿,从而可知鸡有( )只,兔有( )只。
80
30
2
15
5
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
假设20只全是兔。
20只兔总腿数:4×20=80(条)
假设后腿增加:80-50=30(条)
把一只鸡看作一只兔就会增加:4-2=2(条)
鸡:30÷2=15(只)
兔:20-15=5(只)
答:鸡有15只,兔有5只。
课堂总结
通过今天的学习,你有哪些收获?
我会利用“假设”的策略解决相差关系的问题。
我还知道假设时,要根据条件合理假设,把一种量假设成另一种量。
板书设计
解决问题的策略(2)
假设6个全是小盒 假设6个全是大盒
少:8个 多8×5=40(个)
总量:80-8=72(个) 总量:80+40=120(个)
小盒:72÷6=12(个) 大盒:120÷6=20(个)
大盒:12+8=20(个) 小盒:20-8=12(个)
答:大盒里装了20个,每个小盒装12个。
假设→调整→推算
作业布置
完成教材71页“练一练”习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
解决问题的策略(2)
苏教版六年级上册
教学目标
1.学习目标描述:学会用“假设”的策略理解题意、分析数量关系,并能根据问题的特点确定合理的解题步骤。
2.学习内容分析:本课时是用策略解决问题的第二课时,在第一课时里尝试了用替换的策略解决问题的方法,这节课是在进一步感受用策略解决问题的思路和步骤这一思考方法,从而生成和进一步巩固“假设”策略这一思考方法。
教学目标
3.学科核心素养分析:使学生在对解决实际问题过程的不断反思中,感受“假设”策略对于解决特定问题的价值,进一步发展分析、综合和简单推理能力;进一步积累解决问题的经验,增强解决问题的策略意识,获得解决问题的成功体验,提高学好数学的信心。
新知导入
在1个大盒和4个同样的小盒里装满球,正好是90个。如果2个小盒与1个大盒装的一样多,那么大盒里装了多少个球?每个小盒呢?
怎样理解题中数量之间的关系?
1个大盒+4个小盒=90个
2个小盒=1个大盒
你准备怎样解决这个问题呢?与同伴说说自己的想法。
新知导入
在1个大盒和4个同样的小盒里装满球,正好是90个。如果2个小盒与1个大盒装的一样多,那么大盒里装了多少个球?每个小盒呢?
假设把球都装入小盒。
1个大盒+4个小盒=90个
2个小盒
90÷(4÷2+1)=30(个)
答:每个大盒里装了30个球,每个小盒里装了15个球。
30÷2=15(个)
新知导入
在1个大盒和4个同样的小盒里装满球,正好是90个。如果2个小盒与1个大盒装的一样多,那么大盒里装了多少个球?每个小盒呢?
假设把球都装入大盒。
1个大盒+4个小盒=90个
2个大盒
90÷(2+4)=15(个)
答:每个大盒里装了30个球,每个小盒里装了15个球。
15×2=30(个)
新知导入
通过假设替换,可以转化问题,使数量关系变得简单。
如果把上题中的已知条件稍微改一下,又该怎样解答呢?
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
80个
读一读,说说这题告诉了我们哪些条件,要求什么问题?
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
怎样理解题意中的数量关系呢?
1个大盒里的球的个数+5个小盒里球的个数=80
1个大盒里球的个数-8=1个小盒里球的个数
1个小盒里球的个数+8=1个大盒里球的个数
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
合作提示:
你能根据假设后的数量关系想想怎样解决这个问题?并与小组学生交流自己的想法。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
假设6个全是小盒。
如果假设6个全是小盒,球的总数会发生怎样的变化?
假设6个全是小盒,也就是把1个大盒换成小盒。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
每个大盒比每个小盒多装8个
6个全是小盒,这样球的总数比80少。
把1个大盒换成小盒
球的总数比80少8个
6个小盒里球的总数:80-8=72(个)
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
6个小盒里球的总数:80-8=72(个)
每个小盒里装:72÷6=12(个)
每个大盒里装:12+8=20(个)
检验:20+12×5=80(个)
答:大盒里装了20个,每个小盒装12个。
结合题意,检验一下答案是否正确。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
还可以假设6个全是大盒。
如果假设6个全是大盒,球的总数会发生怎样的变化?
6个全是大盒,球的总数比80多。
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
每个大盒比每个小盒多装8个。
把5个小盒换成大盒,球的总数比80多8×5=40(个)。
6个大盒里球的总数是:80+40=120(个)
新知讲解
在1个大盒和5个同样的小盒里装满球,正好是80个。每个大盒比每个小盒多装8个,大盒里装了多少个球?每个小盒呢?
6个大盒里球的总数是:80+40=120(个)
每个大盒里装:120÷6=20(个)
每个小盒里装:20-8=12(个)
检验:20+12×5=80(个)
答:大盒里装了20个,每个小盒装12个。
算出每个大盒里装了多少个球?每个小盒呢?并检验。
新知讲解
刚才我们用两种思路解决了上面的问题,假设6个全是小盒或者假设6个全是大盒,虽然假设的方法不一样,但你发现它们有什么相同的地方?
都是先提出假设。
假设后球的总数与实际数量不一样,这时就需要调整,从而推算出正确的结果。
新知讲解
在进行调整时,我们又是怎么想的?
先算出假设与实际总数相差多少,再算一算每一份相差多少,最后算出调整的数量。
新知讲解
利用“假设”的策略解决相差关系的问题时,先根据解题的需要对已知条件作出假设,通过假设引出差量,然后分析产生差量的原因,找到差量对应的数量来解决问题。
新知讲解
上节课我们学习了例1,明确了假设的策略,今天又学习了例2,用假设的策略解决了另一类比较复杂的问题。回顾例1和例2解决问题的过程,你有什么体会?
都可以通过假设使数量关系变得简单。
要弄清假设前后的数量关系,注意假设前后总量有没有变化。
要在不同的假设方法中选择比较简单的。
课堂练习
1.填一填。
妈妈用96元钱买了6千克苹果和4千克橘子,如果每千克橘子比每千克苹果便宜1.5元。
(1)假设这10千克全买苹果,就必须( )(填“多”或“少”)付( )元,共付( )元,每千克苹果( )元;
(2)假设这10千克全买橘子,就必须( )(填“多”或“少”)付( )元,共付( )元,每千克橘子( )元。
多
6
102
10.2
少
9
87
8.7
课堂练习
2.有 200 位来宾,坐满了12张圆桌和10张方桌,每张圆桌比每张方桌多坐2人,每张圆桌坐多少人?
假设全坐的是圆桌,把10张方桌换成圆桌,总人数比200多10×2=20(人)。
12张圆桌可坐人数:200+10×2=220(人)
每张圆桌:220÷(12+10)=10(人)
答:每张圆桌坐10人。
课堂练习
2.有 200 位来宾,坐满了12张圆桌和10张方桌,每张圆桌比每张方桌多坐2人,每张圆桌坐多少人?
假设全坐的是方桌,把12张圆桌换成方桌,总人数比200少12×2=24(人)。
12张方桌可坐人数:200-12×2=176(人)
每张方桌:176÷(12+10)=8(人)
每张圆桌:8+2=10(人)
答:每张圆桌坐10人。
课堂练习
3.在3个同样的大盒和4个同样的小盒里装满球,正好是120个。每个大盒比每个小盒多装5个,每个大盒和每个小盒里各装了多少个球?
假设假设7个全是大盒,把4个小盒换成大盒,总数比120多5×4=20(个)。
7个大盒里球的总数:120+5×4=140(个)
每个大盒里装:140÷(3+4)=20(个)
每个小盒里装:20-5=15(个)
答:每个大盒里装20个,每个小盒里装15个。
课堂练习
3.在3个同样的大盒和4个同样的小盒里装满球,正好是120个。每个大盒比每个小盒多装5个,每个大盒和每个小盒里各装了多少个球?
假设假设7个全是小盒,把3个大盒换成小盒,总数比120少5×3=15(个)。
7个小盒里球的总数:120-5×3=105(个)
每个小盒里装:105÷(3+4)=15(个)
每个大盒里装:15+5=20(个)
答:每个大盒里装20个,每个小盒里装15个。
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
思考:鸡和兔一共有20只,一共有50条腿。假设20只全是鸡,一共有( )条腿,这样就会减少( )条腿,这是因为把一只兔看作一只鸡就会减少( )条腿,从而可知兔有( )只,鸡有( )只。
40
10
2
5
15
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
假设20只全是鸡。
20只鸡总腿数:2×20=40(条)
假设后腿减少:50-40=10(条)
把一只兔看作一只鸡就会减少:4-2=2(条)
兔:10÷2=5(只)
鸡:20-5=15(只)
答:鸡有15只,兔有5只。
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
思考:鸡和兔一共有20只,一共有50条腿。假设20只全是兔,一共有( )条腿,这样就会增加( )条腿,这是因为把一只鸡看作一只兔就会增加( )条腿,从而可知鸡有( )只,兔有( )只。
80
30
2
15
5
课堂练习
4.拓展练习:鸡兔同笼,上有20只头,下有50只脚,则鸡兔各有多少只?
假设20只全是兔。
20只兔总腿数:4×20=80(条)
假设后腿增加:80-50=30(条)
把一只鸡看作一只兔就会增加:4-2=2(条)
鸡:30÷2=15(只)
兔:20-15=5(只)
答:鸡有15只,兔有5只。
课堂总结
通过今天的学习,你有哪些收获?
我会利用“假设”的策略解决相差关系的问题。
我还知道假设时,要根据条件合理假设,把一种量假设成另一种量。
板书设计
解决问题的策略(2)
假设6个全是小盒 假设6个全是大盒
少:8个 多8×5=40(个)
总量:80-8=72(个) 总量:80+40=120(个)
小盒:72÷6=12(个) 大盒:120÷6=20(个)
大盒:12+8=20(个) 小盒:20-8=12(个)
答:大盒里装了20个,每个小盒装12个。
假设→调整→推算
作业布置
完成教材71页“练一练”习题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
