黑龙江省大兴安岭呼玛县中2022-2023学年高二上学期8月开学考试数学试题(Word版无答案)
文档属性
| 名称 | 黑龙江省大兴安岭呼玛县中2022-2023学年高二上学期8月开学考试数学试题(Word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 17:09:19 | ||
图片预览


文档简介
大兴安岭呼玛县中2022-2023学年高二上学期8月开学考试
数学试题
一、单项选择题 (本大题共 8 小题, 每小题 5 分, 共 40 分, 在每小题给出的四个选项中, 只有一项是符合 题目要求的)
1. 已知等腰梯形 , 现绕着它的较长底 所在的直线旋转一周, 所得的几何体为 ( )
A. 一个圆台、两个圆锥
B. 一个圆柱、两个圆锥
C. 两个圆台、一个圆柱
D. 两个圆柱、一个圆台
2.已知直线 两个不同的平面 , 下列命题正确的是( )
A. 若 , 则
B. 若 , 则
C. 若 , 则
D. 若 , 则
3. 若 , 且 , 则 和 的夹角是( )
A.
B.
C.
D.
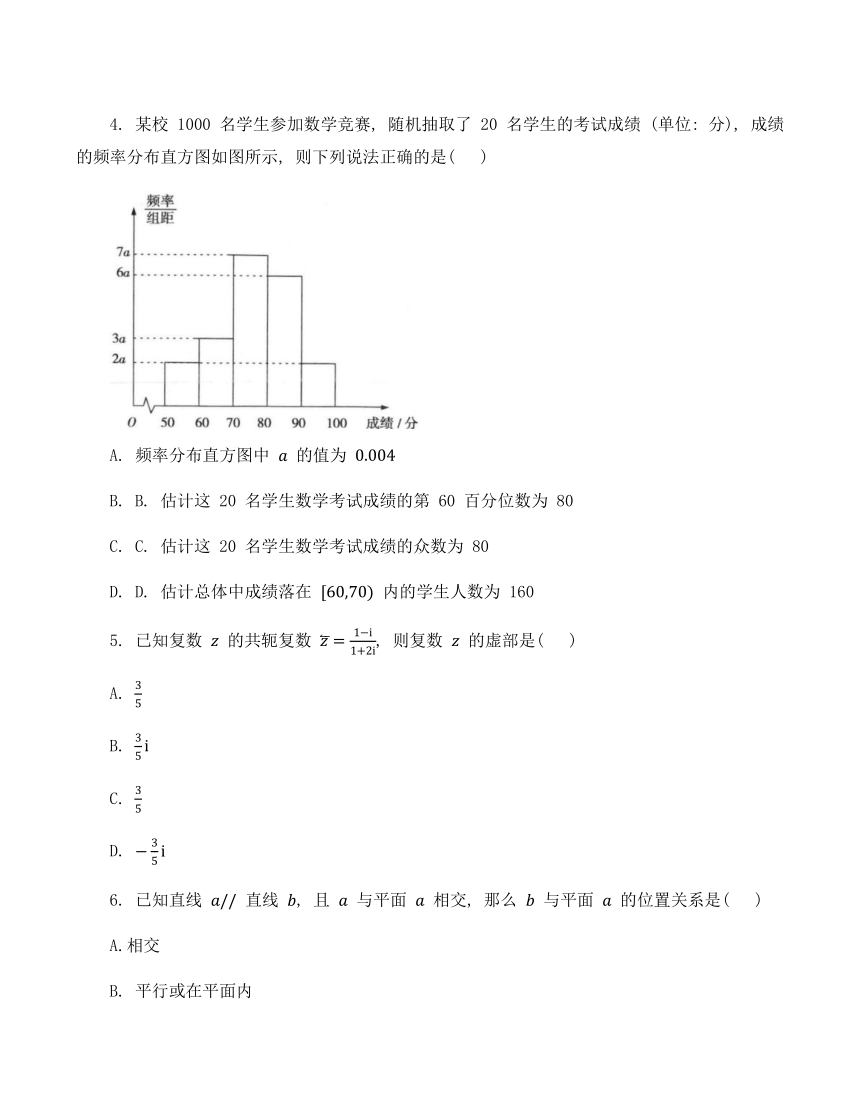
4. 某校 1000 名学生参加数学竞赛, 随机抽取了 20 名学生的考试成绩 (单位: 分), 成绩的频率分布直方图如图所示, 则下列说法正确的是( )
A. 频率分布直方图中 的值为
B. B. 估计这 20 名学生数学考试成绩的第 60 百分位数为 80
C. C. 估计这 20 名学生数学考试成绩的众数为 80
D. D. 估计总体中成绩落在 内的学生人数为 160
5. 已知复数 的共轭复数 , 则复数 的虚部是( )
A.
B.
C.
D.
6. 已知直线 直线 , 且 与平面 相交, 那么 与平面 的位置关系是( )
A.相交
B. 平行或在平面内
C.相交或平行
D.相交或在平面内
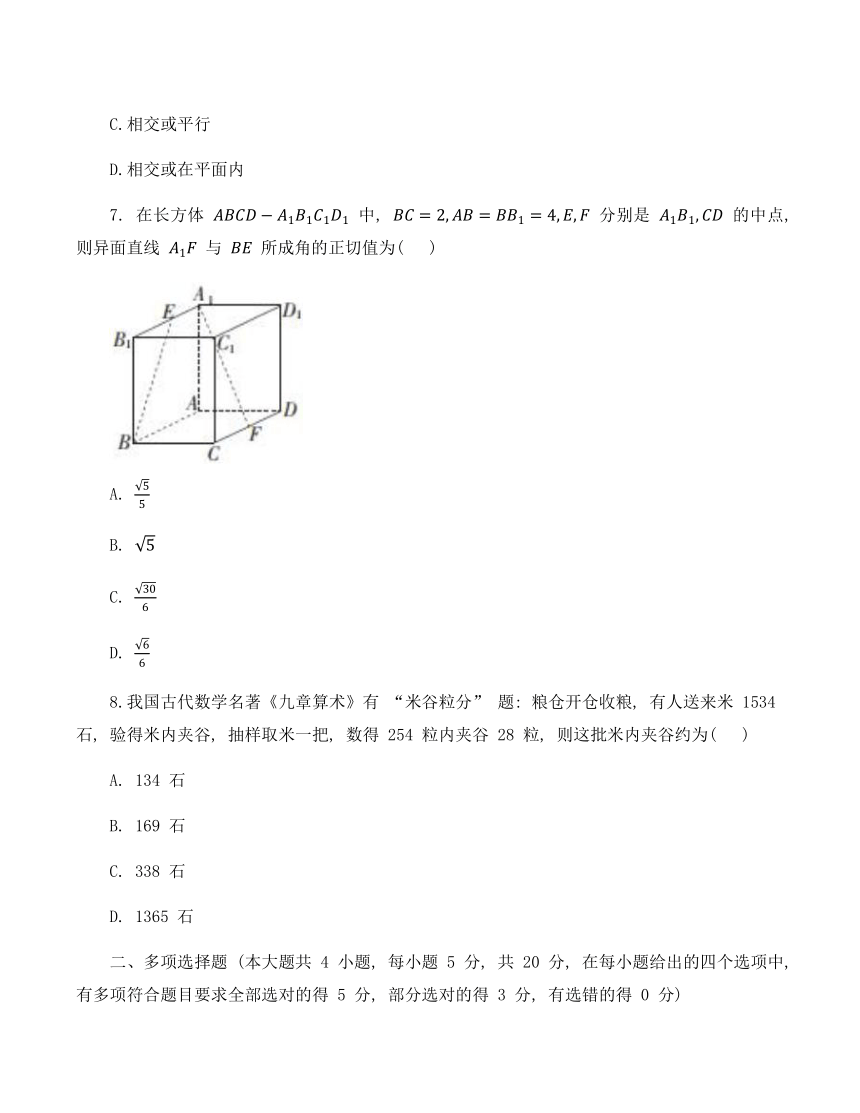
7. 在长方体 中, 分别是 的中点, 则异面直线 与 所成角的正切值为( )
A.
B.
C.
D.
8.我国古代数学名著《九章算术》有 “米谷粒分” 题: 粮仓开仓收粮, 有人送来米 1534 石, 验得米内夹谷, 抽样取米一把, 数得 254 粒内夹谷 28 粒, 则这批米内夹谷约为( )
A. 134 石
B. 169 石
C. 338 石
D. 1365 石
二、多项选择题 (本大题共 4 小题, 每小题 5 分, 共 20 分, 在每小题给出的四个选项中, 有多项符合题目要求全部选对的得 5 分, 部分选对的得 3 分, 有选错的得 0 分)
9. 已知 的内角 所对的边分别为 , 下列四个命题中, 正确的命题是( )
A. 若 , 则 有两解
B. 若 , 则 是等腰三角形
C. 若 在线段 上, 且 , 则 的面积为 8
D. 若 , 动点 在 所在平面内且 , 则 动点 的轨迹的长度为 .
10. 已知复数 , 其中 , 则下列结论正确的是( )
A. 的虚部为
B. 的共轭复数
C. 是关于 的方程 的一个根
D. 若 , 则 在复平面内对应的点的集合是以 为圆心, 3 为半径的圆
11. 已知在正三棱锥 中, 底面 的边长为 4, 为 的中点, , 下列结论正确的为( )
A. 正三棱锥 的体积为
B. 三棱锥 的外接球的表面积为
C. D. 与 所成角的正切值为
D. 与 所成角的正切值为
12. 从甲袋中摸出一个红球的概率是 , 从乙袋中摸出一个红球的概率是 , 从两袋各摸出一个球, 下列 结论正确的是( )
A. 2 个球都是红球的概率为
B. 2 个球不都是红球的概率为
C. 至少有 1 个红球的概率为
D. 2 个球中恰有 1 个红球的概率为
三、填空题 (本大题共 4 小题, 每小题 5 分, 共 20 分)
13. 为做好疫情防控工作, 某市各学校坚持落实 “双测温两报告” 制度, 以下是某宿舍 6 名同学某日上午的体温记录: (单位: ), 则该组数据的第 80 百分位数为 .
14.已知向量 , 若 , 则 .
15. 某射手射中 10 环的概率为 , 那么, 在一次射击训练中, 该射手射击一次不够 10 环的概率为 .
16. 在四面体 中, 是边长为 2 的等边三角形, 是以 为斜边的等腰直角三角形, 平面 平面 , 则四面体 的外接球的表面积为 .
四、解答题(本大题共 6 小题, 共 70 分. 解答时应写出必要的文字说明、证明过程或演算步骤)
17. (10 分) 已知 .
(1) 若 , 求 与 的夹角的余弦值;
(2) 若 , 求实数 的值.
18. (12 分) 某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况, 数据如下表: (单位: 人)
(1) 从该班随机选 1 名同学, 求该同学至少参加上述一个社团的概率;
(2) (2) 在既参加书法社团又参加演讲社团的 8 名同学中, 有 5 名男同学 名 女同学 , 现从这 5 名男同学和 3 名女同学中各随机选 1 人, 求 被选中且 末被选中的概率.
19. (12 分) 如图, 边长为 2 的等边 所在的平面垂直于矩形 所在的平面, , 为 的中点.
(1)证明: ;
(2)求平面 与平面 的夹角的大小;
(3)求点 到平面 的距离.
20. (12 分) 某中学为了解大数据提供的个性化作业质量情况, 随机访问 50 名学生, 根据这 50 名学生对个 性化作业的评分, 绘制频率分布直方图 (如图所示), 其中样本数据分组区 、 .
(1) 求频率分布直方图中 的值;
(2) 估计该中学学生对个性化作业评分不低于 70 的概率;
(3) 从评分在 的受访学生中, 随机抽取 2 人, 求此 2 人评分都在 的概率.
21. (12 分) 在 中, 角 所对的边分别为 , 已知 .
(1) 求角 的大小;
(2) 若 , 求 的面积 的值.
22. (12 分) 如图, 在直角梯形 中, , 且 , 直角梯形 可以通过直角梯形 以直线 为轴旋转得到.
(1) 求证: 平面 平面 ;
(2) 若二面角 的大小为 , 求直线 与平面 所成角的正弦值.
数学试题
一、单项选择题 (本大题共 8 小题, 每小题 5 分, 共 40 分, 在每小题给出的四个选项中, 只有一项是符合 题目要求的)
1. 已知等腰梯形 , 现绕着它的较长底 所在的直线旋转一周, 所得的几何体为 ( )
A. 一个圆台、两个圆锥
B. 一个圆柱、两个圆锥
C. 两个圆台、一个圆柱
D. 两个圆柱、一个圆台
2.已知直线 两个不同的平面 , 下列命题正确的是( )
A. 若 , 则
B. 若 , 则
C. 若 , 则
D. 若 , 则
3. 若 , 且 , 则 和 的夹角是( )
A.
B.
C.
D.
4. 某校 1000 名学生参加数学竞赛, 随机抽取了 20 名学生的考试成绩 (单位: 分), 成绩的频率分布直方图如图所示, 则下列说法正确的是( )
A. 频率分布直方图中 的值为
B. B. 估计这 20 名学生数学考试成绩的第 60 百分位数为 80
C. C. 估计这 20 名学生数学考试成绩的众数为 80
D. D. 估计总体中成绩落在 内的学生人数为 160
5. 已知复数 的共轭复数 , 则复数 的虚部是( )
A.
B.
C.
D.
6. 已知直线 直线 , 且 与平面 相交, 那么 与平面 的位置关系是( )
A.相交
B. 平行或在平面内
C.相交或平行
D.相交或在平面内
7. 在长方体 中, 分别是 的中点, 则异面直线 与 所成角的正切值为( )
A.
B.
C.
D.
8.我国古代数学名著《九章算术》有 “米谷粒分” 题: 粮仓开仓收粮, 有人送来米 1534 石, 验得米内夹谷, 抽样取米一把, 数得 254 粒内夹谷 28 粒, 则这批米内夹谷约为( )
A. 134 石
B. 169 石
C. 338 石
D. 1365 石
二、多项选择题 (本大题共 4 小题, 每小题 5 分, 共 20 分, 在每小题给出的四个选项中, 有多项符合题目要求全部选对的得 5 分, 部分选对的得 3 分, 有选错的得 0 分)
9. 已知 的内角 所对的边分别为 , 下列四个命题中, 正确的命题是( )
A. 若 , 则 有两解
B. 若 , 则 是等腰三角形
C. 若 在线段 上, 且 , 则 的面积为 8
D. 若 , 动点 在 所在平面内且 , 则 动点 的轨迹的长度为 .
10. 已知复数 , 其中 , 则下列结论正确的是( )
A. 的虚部为
B. 的共轭复数
C. 是关于 的方程 的一个根
D. 若 , 则 在复平面内对应的点的集合是以 为圆心, 3 为半径的圆
11. 已知在正三棱锥 中, 底面 的边长为 4, 为 的中点, , 下列结论正确的为( )
A. 正三棱锥 的体积为
B. 三棱锥 的外接球的表面积为
C. D. 与 所成角的正切值为
D. 与 所成角的正切值为
12. 从甲袋中摸出一个红球的概率是 , 从乙袋中摸出一个红球的概率是 , 从两袋各摸出一个球, 下列 结论正确的是( )
A. 2 个球都是红球的概率为
B. 2 个球不都是红球的概率为
C. 至少有 1 个红球的概率为
D. 2 个球中恰有 1 个红球的概率为
三、填空题 (本大题共 4 小题, 每小题 5 分, 共 20 分)
13. 为做好疫情防控工作, 某市各学校坚持落实 “双测温两报告” 制度, 以下是某宿舍 6 名同学某日上午的体温记录: (单位: ), 则该组数据的第 80 百分位数为 .
14.已知向量 , 若 , 则 .
15. 某射手射中 10 环的概率为 , 那么, 在一次射击训练中, 该射手射击一次不够 10 环的概率为 .
16. 在四面体 中, 是边长为 2 的等边三角形, 是以 为斜边的等腰直角三角形, 平面 平面 , 则四面体 的外接球的表面积为 .
四、解答题(本大题共 6 小题, 共 70 分. 解答时应写出必要的文字说明、证明过程或演算步骤)
17. (10 分) 已知 .
(1) 若 , 求 与 的夹角的余弦值;
(2) 若 , 求实数 的值.
18. (12 分) 某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况, 数据如下表: (单位: 人)
(1) 从该班随机选 1 名同学, 求该同学至少参加上述一个社团的概率;
(2) (2) 在既参加书法社团又参加演讲社团的 8 名同学中, 有 5 名男同学 名 女同学 , 现从这 5 名男同学和 3 名女同学中各随机选 1 人, 求 被选中且 末被选中的概率.
19. (12 分) 如图, 边长为 2 的等边 所在的平面垂直于矩形 所在的平面, , 为 的中点.
(1)证明: ;
(2)求平面 与平面 的夹角的大小;
(3)求点 到平面 的距离.
20. (12 分) 某中学为了解大数据提供的个性化作业质量情况, 随机访问 50 名学生, 根据这 50 名学生对个 性化作业的评分, 绘制频率分布直方图 (如图所示), 其中样本数据分组区 、 .
(1) 求频率分布直方图中 的值;
(2) 估计该中学学生对个性化作业评分不低于 70 的概率;
(3) 从评分在 的受访学生中, 随机抽取 2 人, 求此 2 人评分都在 的概率.
21. (12 分) 在 中, 角 所对的边分别为 , 已知 .
(1) 求角 的大小;
(2) 若 , 求 的面积 的值.
22. (12 分) 如图, 在直角梯形 中, , 且 , 直角梯形 可以通过直角梯形 以直线 为轴旋转得到.
(1) 求证: 平面 平面 ;
(2) 若二面角 的大小为 , 求直线 与平面 所成角的正弦值.
同课章节目录
