2022—2023学年北师大版数学七年级上册 1.1生活中的立体图形 同步测试(word版 含答案)
文档属性
| 名称 | 2022—2023学年北师大版数学七年级上册 1.1生活中的立体图形 同步测试(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 383.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 09:27:33 | ||
图片预览




文档简介
北师大版七年级数学上册第一章1.1生活中的立体图形 同步测试
一.选择题
1.下列几何体:①正方体;②圆柱;③圆锥;④长方体;⑤球;⑥五棱柱,其中有两个底面的是( )
A.②④⑥ B.①②⑥ C.②③⑤ D.①②④⑥
2.如图所示的平面图形绕直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
3.下列几何图形中为圆柱体的是( )
A. B. C. D.
4.下列几何体中,通过下图旋转一周后形成的立体图形是( )
5.下列几何体中,不能由一个平面图形通过旋转得到的是( )
6.如图,模块①由15个棱长为1的小正方体构成,模块②﹣⑥均由4个棱长为1的小正方体构成.现在从模块②﹣⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是( )
A.模块②,⑤,⑥ B.模块③,④,⑥ C.模块②,④,⑤ D.模块③,⑤,⑥
7.正方体的顶点数.面数和棱数分别是( )
A.8.6.12 B.6.8.12 C.8.12.6 D.6.8.10
8.一个正方体体积为125立方厘米,则这个正方体的表面积为( )平方厘米.
A.45 B.125 C.150 D.175
9.如图,有一个棱长是4 cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )
A.变大了 B.变小了 C.没变 D.无法确定变化情
10.将下面的直角梯形绕直线l旋转一周,可以得到如图立体图形的是( )
A. B. C. D.
11.一个圆柱的体积是80cm3,底面积是16cm2,它的高是( )cm.
A.15 B.10 C.5 D.0.2
12.10个棱长为1的正方体木块堆成如图所示的形状,则它的表面积是( )
A.30 B.34 C.36 D.48
二.填空题
13.“枪打一条线,棍打一大片”这个现象说明:______________
14.一个棱柱共有18个顶点,所有的侧棱长的和是72厘米,则每条侧棱长
是 厘米.
15.五棱柱有 个面, 个顶点, 条侧棱,n棱柱有 个面, 个顶点, 条棱.
16.已知有一个长为5,宽为3的长方形,若以这个长方形的长边所在的直线为轴,将它旋转一周,则所得的几何体的体积为 (结果保留π).
17.将如图所示半圆形薄片绕轴旋转一周,得到的几何体是 ,这一现象说明 .
18.如图所示,一个长方体的长.宽.高分别是3cm,3cm,5cm,在这个长方体每个面的中心位置,从前到后,从左到右,从上到下分别打一个边长为1cm的正方形通孔,那么打孔后的长方体的表面积为 cm2.
三.解答题
19.补画长方体.
20.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
21.如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
22.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
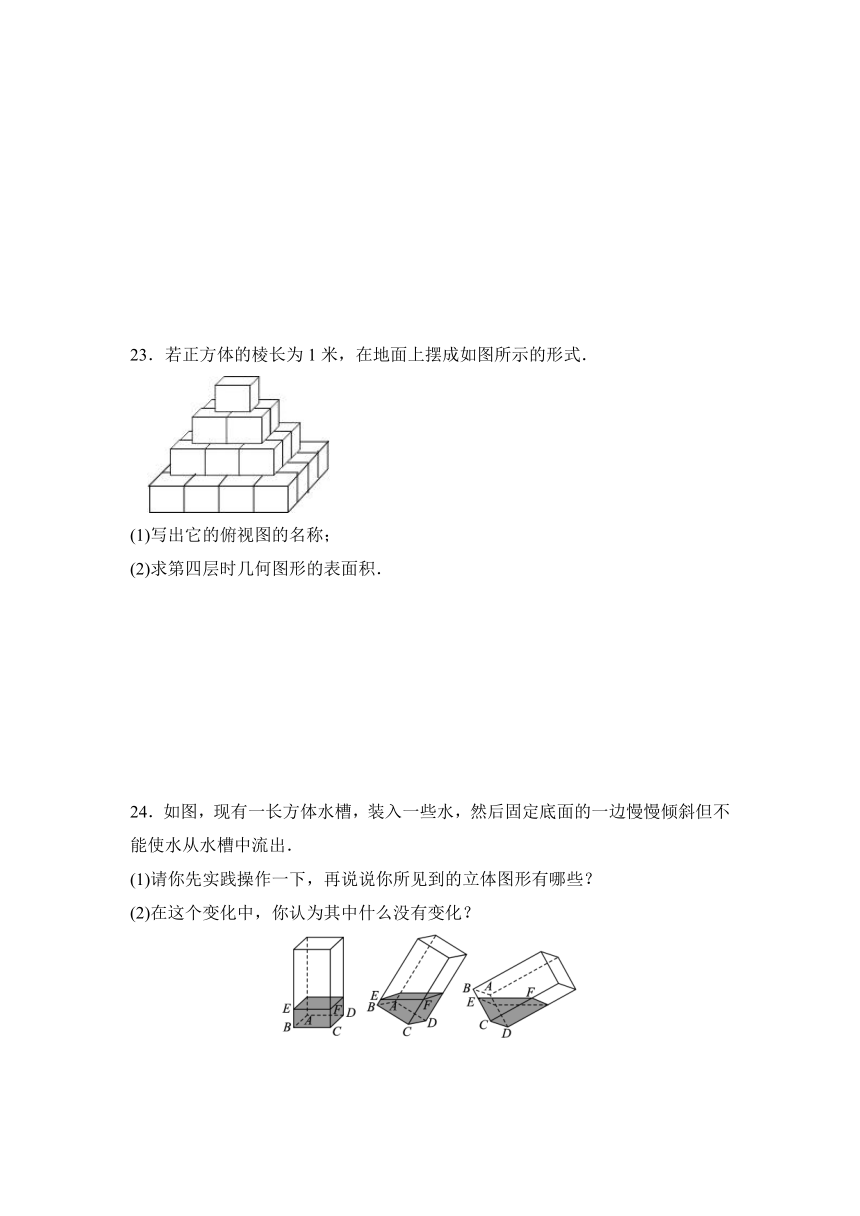
23.若正方体的棱长为1米,在地面上摆成如图所示的形式.
(1)写出它的俯视图的名称;
(2)求第四层时几何图形的表面积.
24.如图,现有一长方体水槽,装入一些水,然后固定底面的一边慢慢倾斜但不能使水从水槽中流出.
(1)请你先实践操作一下,再说说你所见到的立体图形有哪些?
(2)在这个变化中,你认为其中什么没有变化?
25.新年晚会的会场上悬挂了许多五彩缤纷的小装饰品,其中有各种各样的立体图形,如图:
请你数一数上图中每个多面体具有的顶点数(V),棱数(E)和面数(F),并把结果计入下表中.
名称 各面形状 顶点数(V) 面数(F) 棱数(E) V+F-E
正四面体 正三角形
正方体 正方形
正八面体 正三角形
正十二面体 正五边形 20 12 30 2
北师大版七年级数学上册第一章1.1生活中的立体图形 答案提示
一.选择题
1.下列几何体:①正方体;②圆柱;③圆锥;④长方体;⑤球;⑥五棱柱,其中有两个底面的是( )选:D
A.②④⑥ B.①②⑥ C.②③⑤ D.①②④⑥
2.如图所示的平面图形绕直线l旋转一周,可以得到的立体图形是( )选:C.
A. B. C. D.
3.下列几何图形中为圆柱体的是( ) 选:C
A. B. C. D.
4.下列几何体中,通过下图旋转一周后形成的立体图形是( )选:D
5.下列几何体中,不能由一个平面图形通过旋转得到的是( )选:D
6.如图,模块①由15个棱长为1的小正方体构成,模块②﹣⑥均由4个棱长为1的小正方体构成.现在从模块②﹣⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是()选:A.
A.模块②,⑤,⑥ B.模块③,④,⑥ C.模块②,④,⑤ D.模块③,⑤,⑥
7.正方体的顶点数.面数和棱数分别是( ) 选:A
A.8.6.12 B.6.8.12 C.8.12.6 D.6.8.10
8.一个正方体体积为125立方厘米,则这个正方体的表面积为( )平方厘米.
选:C.
A.45 B.125 C.150 D.175
9.如图,有一个棱长是4 cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )选:C
A.变大了 B.变小了 C.没变 D.无法确定变化情
10.将下面的直角梯形绕直线l旋转一周,可以得到如图立体图形的是( )选:B.
A. B. C. D.
11.一个圆柱的体积是80cm3,底面积是16cm2,它的高是( )cm.选:C.
A.15 B.10 C.5 D.0.2
12.10个棱长为1的正方体木块堆成如图所示的形状,则它的表面积是( )
A.30 B.34 C.36 D.48
12.C
【解答】根据以上分析露出的面积=5+4×2+2+4×2+3+2×1+2+6=36.【分析】第一层露出5个面;第二层露出4×2+2个面;第三层露出4×2+3+2×1+2;底面6个面.
二.填空题
13.“枪打一条线,棍打一大片”这个现象说明:______________
13.点动成线,线动成面
14.一个棱柱共有18个顶点,所有的侧棱长的和是72厘米,则每条侧棱长
是 厘米.14.8.
15.五棱柱有 个面, 个顶点, 条侧棱,n棱柱有 个面, 个顶点, 条棱.15.7,10,5,(n+2),2n,3n.
16.已知有一个长为5,宽为3的长方形,若以这个长方形的长边所在的直线为轴,将它旋转一周,则所得的几何体的体积为 45π (结果保留π).
17.将如图所示半圆形薄片绕轴旋转一周,得到的几何体是 ,这一现象说明 .17.球,面动成体.
18.如图所示,一个长方体的长.宽.高分别是3cm,3cm,5cm,在这个长方体每个面的中心位置,从前到后,从左到右,从上到下分别打一个边长为1cm的正方形通孔,那么打孔后的长方体的表面积为 104 cm2.
解:打孔后的长方体的表面积=2×(3×3+3×5+3×5)﹣6+8×(1×1)+8×(1×1)+8×(2×1)=104(cm2)
三.解答题
19.补画长方体.
解:如图所示:
.
20.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 3 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
故答案为:3.
(2)以AB为轴:
×3×82×4=×3×64×4=256(立方厘米);
以BC为轴:
×3×42×8=×3×16×8=128(立方厘米).
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
21.如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
21.解:(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;
(2)绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;
(3)绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.
故答案为:圆柱;面动成体.
22.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
解:绕长所在的直线旋转一周得到圆柱体积为:
π×32×4=36π(cm3),
绕宽所在的直线旋转一周得到圆柱体积为:
π×42×3=48π(cm3),
答:得到的圆柱体的体积是36πcm3或者48πcm3.
23.若正方体的棱长为1米,在地面上摆成如图所示的形式.
(1)写出它的俯视图的名称;
(2)求第四层时几何图形的表面积.
23.(1)正方形,解答:它的俯视图是边长为4米的正方形;
(2)56m2
解答:S=(1+2+3+4)×12×4+4×4=40+16=56m2 .
24.如图,现有一长方体水槽,装入一些水,然后固定底面的一边慢慢倾斜但不能使水从水槽中流出.
(1)请你先实践操作一下,再说说你所见到的立体图形有哪些?
(2)在这个变化中,你认为其中什么没有变化?
24.解:(1)长方体、四棱柱、三棱柱.
(2)水的体积不变,即水槽中的水构成的柱体的体积不变.
25.新年晚会的会场上悬挂了许多五彩缤纷的小装饰品,其中有各种各样的立体图形,如图:
请你数一数上图中每个多面体具有的顶点数(V),棱数(E)和面数(F),并把结果计入下表中.
名称 各面形状 顶点数(V) 面数(F) 棱数(E) V+F-E
正四面体 正三角形
正方体 正方形
正八面体 正三角形
正十二面体 正五边形 20 12 30 2
解:
从左到右,从上到下依次填:4,4,6,2;8,6,12,2;6,8,12,2.
一.选择题
1.下列几何体:①正方体;②圆柱;③圆锥;④长方体;⑤球;⑥五棱柱,其中有两个底面的是( )
A.②④⑥ B.①②⑥ C.②③⑤ D.①②④⑥
2.如图所示的平面图形绕直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
3.下列几何图形中为圆柱体的是( )
A. B. C. D.
4.下列几何体中,通过下图旋转一周后形成的立体图形是( )
5.下列几何体中,不能由一个平面图形通过旋转得到的是( )
6.如图,模块①由15个棱长为1的小正方体构成,模块②﹣⑥均由4个棱长为1的小正方体构成.现在从模块②﹣⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是( )
A.模块②,⑤,⑥ B.模块③,④,⑥ C.模块②,④,⑤ D.模块③,⑤,⑥
7.正方体的顶点数.面数和棱数分别是( )
A.8.6.12 B.6.8.12 C.8.12.6 D.6.8.10
8.一个正方体体积为125立方厘米,则这个正方体的表面积为( )平方厘米.
A.45 B.125 C.150 D.175
9.如图,有一个棱长是4 cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )
A.变大了 B.变小了 C.没变 D.无法确定变化情
10.将下面的直角梯形绕直线l旋转一周,可以得到如图立体图形的是( )
A. B. C. D.
11.一个圆柱的体积是80cm3,底面积是16cm2,它的高是( )cm.
A.15 B.10 C.5 D.0.2
12.10个棱长为1的正方体木块堆成如图所示的形状,则它的表面积是( )
A.30 B.34 C.36 D.48
二.填空题
13.“枪打一条线,棍打一大片”这个现象说明:______________
14.一个棱柱共有18个顶点,所有的侧棱长的和是72厘米,则每条侧棱长
是 厘米.
15.五棱柱有 个面, 个顶点, 条侧棱,n棱柱有 个面, 个顶点, 条棱.
16.已知有一个长为5,宽为3的长方形,若以这个长方形的长边所在的直线为轴,将它旋转一周,则所得的几何体的体积为 (结果保留π).
17.将如图所示半圆形薄片绕轴旋转一周,得到的几何体是 ,这一现象说明 .
18.如图所示,一个长方体的长.宽.高分别是3cm,3cm,5cm,在这个长方体每个面的中心位置,从前到后,从左到右,从上到下分别打一个边长为1cm的正方形通孔,那么打孔后的长方体的表面积为 cm2.
三.解答题
19.补画长方体.
20.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
21.如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
22.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
23.若正方体的棱长为1米,在地面上摆成如图所示的形式.
(1)写出它的俯视图的名称;
(2)求第四层时几何图形的表面积.
24.如图,现有一长方体水槽,装入一些水,然后固定底面的一边慢慢倾斜但不能使水从水槽中流出.
(1)请你先实践操作一下,再说说你所见到的立体图形有哪些?
(2)在这个变化中,你认为其中什么没有变化?
25.新年晚会的会场上悬挂了许多五彩缤纷的小装饰品,其中有各种各样的立体图形,如图:
请你数一数上图中每个多面体具有的顶点数(V),棱数(E)和面数(F),并把结果计入下表中.
名称 各面形状 顶点数(V) 面数(F) 棱数(E) V+F-E
正四面体 正三角形
正方体 正方形
正八面体 正三角形
正十二面体 正五边形 20 12 30 2
北师大版七年级数学上册第一章1.1生活中的立体图形 答案提示
一.选择题
1.下列几何体:①正方体;②圆柱;③圆锥;④长方体;⑤球;⑥五棱柱,其中有两个底面的是( )选:D
A.②④⑥ B.①②⑥ C.②③⑤ D.①②④⑥
2.如图所示的平面图形绕直线l旋转一周,可以得到的立体图形是( )选:C.
A. B. C. D.
3.下列几何图形中为圆柱体的是( ) 选:C
A. B. C. D.
4.下列几何体中,通过下图旋转一周后形成的立体图形是( )选:D
5.下列几何体中,不能由一个平面图形通过旋转得到的是( )选:D
6.如图,模块①由15个棱长为1的小正方体构成,模块②﹣⑥均由4个棱长为1的小正方体构成.现在从模块②﹣⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体.下列四个方案中,符合上述要求的是()选:A.
A.模块②,⑤,⑥ B.模块③,④,⑥ C.模块②,④,⑤ D.模块③,⑤,⑥
7.正方体的顶点数.面数和棱数分别是( ) 选:A
A.8.6.12 B.6.8.12 C.8.12.6 D.6.8.10
8.一个正方体体积为125立方厘米,则这个正方体的表面积为( )平方厘米.
选:C.
A.45 B.125 C.150 D.175
9.如图,有一个棱长是4 cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )选:C
A.变大了 B.变小了 C.没变 D.无法确定变化情
10.将下面的直角梯形绕直线l旋转一周,可以得到如图立体图形的是( )选:B.
A. B. C. D.
11.一个圆柱的体积是80cm3,底面积是16cm2,它的高是( )cm.选:C.
A.15 B.10 C.5 D.0.2
12.10个棱长为1的正方体木块堆成如图所示的形状,则它的表面积是( )
A.30 B.34 C.36 D.48
12.C
【解答】根据以上分析露出的面积=5+4×2+2+4×2+3+2×1+2+6=36.【分析】第一层露出5个面;第二层露出4×2+2个面;第三层露出4×2+3+2×1+2;底面6个面.
二.填空题
13.“枪打一条线,棍打一大片”这个现象说明:______________
13.点动成线,线动成面
14.一个棱柱共有18个顶点,所有的侧棱长的和是72厘米,则每条侧棱长
是 厘米.14.8.
15.五棱柱有 个面, 个顶点, 条侧棱,n棱柱有 个面, 个顶点, 条棱.15.7,10,5,(n+2),2n,3n.
16.已知有一个长为5,宽为3的长方形,若以这个长方形的长边所在的直线为轴,将它旋转一周,则所得的几何体的体积为 45π (结果保留π).
17.将如图所示半圆形薄片绕轴旋转一周,得到的几何体是 ,这一现象说明 .17.球,面动成体.
18.如图所示,一个长方体的长.宽.高分别是3cm,3cm,5cm,在这个长方体每个面的中心位置,从前到后,从左到右,从上到下分别打一个边长为1cm的正方形通孔,那么打孔后的长方体的表面积为 104 cm2.
解:打孔后的长方体的表面积=2×(3×3+3×5+3×5)﹣6+8×(1×1)+8×(1×1)+8×(2×1)=104(cm2)
三.解答题
19.补画长方体.
解:如图所示:
.
20.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到 3 种大小不同的几何体?
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)
解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.
故答案为:3.
(2)以AB为轴:
×3×82×4=×3×64×4=256(立方厘米);
以BC为轴:
×3×42×8=×3×16×8=128(立方厘米).
答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.
21.如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
21.解:(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;
(2)绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;
(3)绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.
故答案为:圆柱;面动成体.
22.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)
解:绕长所在的直线旋转一周得到圆柱体积为:
π×32×4=36π(cm3),
绕宽所在的直线旋转一周得到圆柱体积为:
π×42×3=48π(cm3),
答:得到的圆柱体的体积是36πcm3或者48πcm3.
23.若正方体的棱长为1米,在地面上摆成如图所示的形式.
(1)写出它的俯视图的名称;
(2)求第四层时几何图形的表面积.
23.(1)正方形,解答:它的俯视图是边长为4米的正方形;
(2)56m2
解答:S=(1+2+3+4)×12×4+4×4=40+16=56m2 .
24.如图,现有一长方体水槽,装入一些水,然后固定底面的一边慢慢倾斜但不能使水从水槽中流出.
(1)请你先实践操作一下,再说说你所见到的立体图形有哪些?
(2)在这个变化中,你认为其中什么没有变化?
24.解:(1)长方体、四棱柱、三棱柱.
(2)水的体积不变,即水槽中的水构成的柱体的体积不变.
25.新年晚会的会场上悬挂了许多五彩缤纷的小装饰品,其中有各种各样的立体图形,如图:
请你数一数上图中每个多面体具有的顶点数(V),棱数(E)和面数(F),并把结果计入下表中.
名称 各面形状 顶点数(V) 面数(F) 棱数(E) V+F-E
正四面体 正三角形
正方体 正方形
正八面体 正三角形
正十二面体 正五边形 20 12 30 2
解:
从左到右,从上到下依次填:4,4,6,2;8,6,12,2;6,8,12,2.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
