2022—2023学年北师大版数学九年级上册 1.3正方形的性质与判定 同步测试(word版 含答案)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级上册 1.3正方形的性质与判定 同步测试(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 465.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 09:30:57 | ||
图片预览




文档简介
北师大版九年级数学上册第一章1.3正方形的性质与判定 同步测试
一.选择题
1.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
2.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
4.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
5.若正方形的周长为40,则其对角线长为( )
A.100 B.20 C.10 D.10
6.如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )
A.45° B.22.5° C.67.5° D.75°
下列说法不正确的是( )
A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形
8.如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
如图,正方形ABCD绕点A逆时针旋转45°与正方形AEFG重合,EF与CD交于点M,得四边形AEMD,正方形ABCD的边长为2,则两正方形重合部分(阴影部分)的面积为( )
A.4 -4 B.4 +4 C.8-4 D.+1
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
11.如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )
A.45° B.55° C.60° D.75°
12.如图,菱形ABCD中,,点P从点B出发,沿折线方向移动,移动到点D停止.在形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
二.填空题
13.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.
14.在正方形ABCD中,E为BC上一点,EF⊥AC,EG⊥BD,垂足分别为F、G,如果AB=cm,那么EF+EG的长为______.
15.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________(只填写序号)
16.如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
17.对角线________的菱形是正方形,对角线________的矩形是正方形,
对角线________________的平行四边形是正方形,
对角线 的四边形是正方形.
18.如图所示,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以AE为边作第三个正方形AEGM,…已知正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3,…Sn(n为正整数),那么第8个正方形面积S8= .
三.解答题
19.如图,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.
20.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,且AF=CE.
(1)四边形ACEF是平行四边形吗?说明理由;
(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
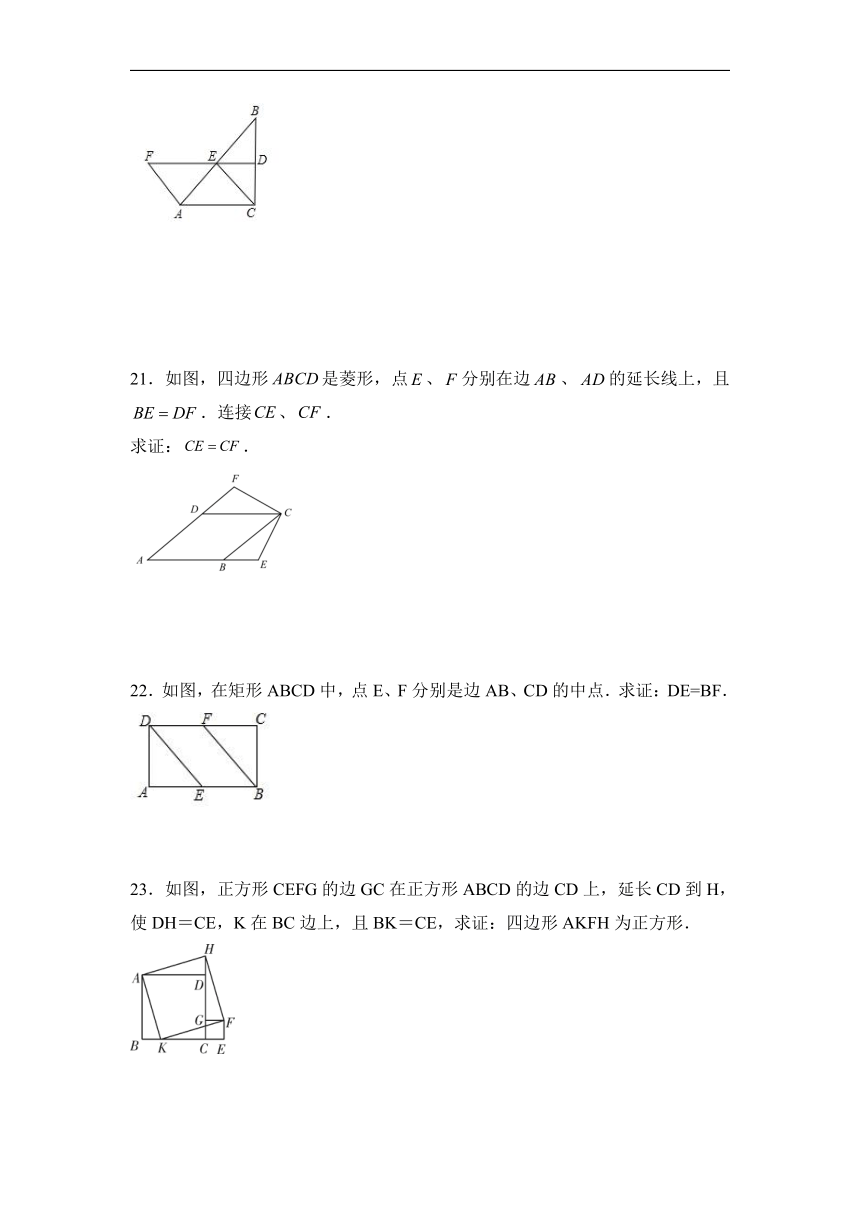
21.如图,四边形是菱形,点、分别在边、的延长线上,且.连接、.
求证:.
22.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.
23.如图,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
24.如图①,在正方形ABCD中,E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是________,位置关系是________;
(2)如图②,若E,F分别是边CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请做出判断并给予证明;
(3)如图③,若E,F分别是边BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
25.如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形
26.如图,E是矩形ABCD的边BC的中点,P是边AD上的一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?并证明;
(2)在(1)的条件下,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?
北师大版九年级数学上册第一章1.3正方形的性质与判定 答案提示
一.选择题
1.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
解:A.不正确,菱形的对角线不相等;
B.不正确,菱形的对角线不相等,矩形的对角线不垂直;
C.正确,三者均具有此性质;
D.不正确,矩形的四边不相等,菱形的四个角不相等;
故选C.
2.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
解:设CE=x,则BE=3-x,
由折叠性质可知,
EF=CE=x,DF=CD=AB=5
在Rt△DAF中,AD=3,DF=5,
∴AF=,
∴BF=AB-AF=5-4=1,
在Rt△BEF中,BE2+BF2=EF2,
即(3-x)2+12=x2,
解得x=,
故选:D.
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ) 选:B.
A.选①② B.选②③ C.选①③ D.选②④
4.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
解:由题意设CH=xcm,则DH=EH=(9﹣x)cm,
∵BE:EC=2:1,
∴CE=BC=3cm
∴在Rt△ECH中,EH2=EC2+CH2,
即(9﹣x)2=32+x2,
解得:x=4,即CH=4cm.故选:C.
5.若正方形的周长为40,则其对角线长为( )
A.100 B.20 C.10 D.10
解: ∵正方形的周长为40,∴正方形的边长为10,∴对角线长为10
故选C.
6.如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )选:B.
A.45° B.22.5° C.67.5° D.75°
下列说法不正确的是( )选:D.
A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形
8.如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
解: ∵HF⊥BC,EG⊥AB,
∴∠BEO=∠BFO=90°,
∵∠A=120°,
∴∠B=60°,
∴∠EOF=120°,∠EOH=60°,
由菱形的对边平行,得HF⊥AD,EG⊥CD,
因为O点是菱形ABCD的对称中心,
∴O点到各边的距离相等,即OE=OF=OG=OH,
∴∠OEF=∠OFE=30°,∠OEH=∠OHE=60°,
∴∠HEF=∠EFG=∠FGH=∠EHG=90°,
所以四边形EFGH是矩形;
设OE=OF=OG=OH=x,
∴EG=HF=2x,,
如图,连接AC,则AC经过点O,
可得三角形ABC是等边三角形,
∴∠BAC=60°,AC=AB=2,
∴OA=1,∠AOE=30°,
∴AE=,
∴x=OE=
∴四边形EFGH的周长为EF+FG+GH+HE=,
故选A.
如图,正方形ABCD绕点A逆时针旋转45°与正方形AEFG重合,EF与CD交于点M,得四边形AEMD,正方形ABCD的边长为2,则两正方形重合部分(阴影部分)的面积为( )选:A.
A.4 -4 B.4 +4 C.8-4 D.+1
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )选:D.
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
11.如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )
A.45° B.55° C.60° D.75°
解: ∵四边形ABCD是正方形,
∴AB=AD,∠BAS=90°,
∵△AED是等边三角形,
∴∠AED=∠EAD=60°,AE=AD,
∴∠BAE=150°,AB=AE,
∴∠ABE=∠AEB=(180°-150°)=15°,
∴∠DFE=∠AFB=90°-15°=75°,
故选D.
12.如图,菱形ABCD中,,点P从点B出发,沿折线方向移动,移动到点D停止.在形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
解:连接AC,BD,如图所示.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B.
∵∠B=60°,
∴∠D=∠B=60°.
∴和都是等边三角形.
点P在移动过程中,依次共有四个特殊位置:
(1)当点P移动到BC边的中点时,记作.
∵是等边三角形,是 BC的中点,
∴.
∴.
∴是直角三角形.
(2)当点P与点C重合时,记作.
此时,是等边三角形;
(3)当点P移动到CD边的中点时,记为.
∵和都是等边三角形,
∴.
∴是直角三角形.
(4)当点P与点D重合时,记作.
∵,
∴是等腰三角形.
综上,形状的变化过程中,依次出现的特殊三角形是:
直角三角形→等边三角形→直角三角形→等腰三角形.
故选:C
二.填空题
13.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.①③④
14.在正方形ABCD中,E为BC上一点,EF⊥AC,EG⊥BD,垂足分别为F、G,如果AB=cm,那么EF+EG的长为______.5cm;
15.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________(只填写序号) ②③或①④
解: 有6种选法:(1)①②:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(2)②③:由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误;
(3)①③:由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(4)②④:由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
(5)①④:由①得有一组邻边相等的平行四边形是菱形,由④得对角线互相垂直的平行四边形是菱形,所以不能得出平行四边形ABCD是正方形,错误;
(6)③④:由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
综上所述:错误的是:②③或①④;
故答案为:②③或①④.
16.如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
解:∵菱形ABCD的对角线AC、BD相交于点O,且AC=8,DB=6,
∴AO=4,DO=3,∠AOD=90°,
∴AD=5,
在 中,由等面积法得: ,
∴
故答案为: .
17.对角线________的菱形是正方形,对角线________的矩形是正方形,
对角线________________的平行四边形是正方形,
对角线 的四边形是正方形.
相等 互相垂直 互相垂直且相等 互相垂直平分且相等
18.如图所示,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以AE为边作第三个正方形AEGM,…已知正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3,…Sn(n为正整数),那么第8个正方形面积S8= .
解:根据题意可得:第n个正方形的边长是第(n﹣1)个的倍;故面积是第(n﹣1)个的2倍,已知第一个面积为1;则那么第8个正方形面积S8=27=128.
故答案为128.
三.解答题
19.如图,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.
证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°.
∵BF⊥CE,∴∠BCE+∠CBG=90°.
∵∠ABF+∠CBG=90°,∴∠BCE=∠ABF.
在△BCE和△ABF中,
∠BCE=∠ABF,BC=AB,∠CBE=∠A,
∴△BCE≌△ABF(ASA),∴AF=BE.
20.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,且AF=CE.
(1)四边形ACEF是平行四边形吗?说明理由;
(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
解:(1)四边形ACEF是平行四边形;
理由:∵DE垂直平分BC,
∴D为BC的中点,ED⊥BC,
又∵AC⊥BC,
∴ED∥AC,
∴E为AB中点,
∴ED是△ABC的中位线.
∴BE=AE,FD∥AC.
∴BD=CD,
∴Rt△ABC中,CE是斜边AB的中线,
∴CE=AE=AF.
∴∠F=∠5=∠1=∠2.
∴∠FAE=∠AEC.
∴AF∥EC.
又∵AF=EC,
∴四边形ACEF是平行四边形;
(2)理由:∵∠ACB=90°,∠B=30°,
∴AC=AB,
由(1)知CE=AB,∴AC=CE
又四边形ACEF为平行四边形
∴四边形ACEF为菱形;
解:(3)四边形ACEF不可能是正方形,
∵∠ACB=90°,
∴∠ACE<∠ACB,
即∠ACE<90°,不能为直角,
所以四边形ACEF不可能是正方形
21.如图,四边形是菱形,点、分别在边、的延长线上,且.连接、.
求证:.
解:∵四边形ABCD是菱形,
∴BC=CD,∠ADC=∠ABC,
∴∠CDF=∠CBE,
在△BEC和△DFC中,
,
∴△BEC≌△DFC(SAS),
∴CE=CF.
22.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
又E、F分别是边AB、CD的中点,
∴DF=BE,
又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE=BF.
23.如图,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
证明:∵四边形ABCD和四边形CEFG是正方形,∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,∴∠ADH=∠HGF=∠E=∠B=90°.又∵DH=CE,BK=CE,∴BK=GF=DH=EF,KE=GH=AB=AD,∴△ABK≌△KEF≌△HGF≌△ADH,∴AK=KF=HF=AH,∠BAK=∠DAH.∵∠BAD=90°,∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,∴四边形AKFH为正方形.
24.如图①,在正方形ABCD中,E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是________,位置关系是________;
(2)如图②,若E,F分别是边CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请做出判断并给予证明;
(3)如图③,若E,F分别是边BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
解:(1)相等 互相平行
(2)成立.
证明:如图,过点G作GH⊥CB交其延长线于点H.
∵EG⊥DE,
∴∠GEH+∠DEC=90°.
∵∠GEH+∠HGE=90°,
∴∠DEC=∠HGE.
在△HGE与△CED中,
∠GHE=∠DCE=90°,∠HGE=∠DEC,EG=DE,
∴△HGE≌△CED,∴GH=CE,HE=CD.
∵CE=BF,∴GH=BF.
又∵GH∥BF且∠GHE=90°,
∴四边形GHBF是矩形,
∴FG=BH,FG∥CH,∴FG∥CE.
∵四边形ABCD是正方形,∴CD=BC,
∴HE=BC,
∴HE+EB=BC+EB,
∴BH=CE,∴FG=CE.
(3)成立.FG=CE,FG∥CE.
25.如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形
解:∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵∠DCE=90°,∴∠ACD+∠ACE=90°,
∴∠BCD=∠ACE,
在△CBD与△CAE中,
CB=CA
∠BCD=∠ACE
CD=CE
∴△CBD≌△CAE(SAS),
∴∠B=∠CAE,
∵∠B+∠BAC=90°,∴∠BAC+∠EAC=90°,∴AB⊥AE;
解: (2)证明:∵点D为AB中点,
∴∠ADC=90°,
∵∠DCE=90°,∠BAE=90°,
∴四边形ADCE是矩形,
∴CD=CE,∴四边形ADCE是正方形
26.如图,E是矩形ABCD的边BC的中点,P是边AD上的一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?并证明;
(2)在(1)的条件下,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?
解:(1)当矩形ABCD的长是宽的2倍时,四边形PHEF是矩形.
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
∵E是BC的中点,
∴AB=BE=EC=CD,则△ABE,△DCE均是等腰直角三角形,
∴∠AEB=∠DEC=45°,
∴∠AED=90°.
在四边形PHEF中,∵∠PFE=∠FEH=∠EHP=90°,
∴四边形PHEF是矩形.
(2)当点P是AD的中点时,矩形PHEF变为正方形.理由如下:
由(1)可得∠BAE=∠CDE=45°,
∴∠FAP=∠HDP=45°.
又∵∠AFP=∠DHP=90°,AP=DP,
∴Rt△AFP≌Rt△DHP,
∴PF=PH,
∴矩形PHEF是正方形.
一.选择题
1.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
2.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.选①② B.选②③ C.选①③ D.选②④
4.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
5.若正方形的周长为40,则其对角线长为( )
A.100 B.20 C.10 D.10
6.如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )
A.45° B.22.5° C.67.5° D.75°
下列说法不正确的是( )
A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形
8.如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
如图,正方形ABCD绕点A逆时针旋转45°与正方形AEFG重合,EF与CD交于点M,得四边形AEMD,正方形ABCD的边长为2,则两正方形重合部分(阴影部分)的面积为( )
A.4 -4 B.4 +4 C.8-4 D.+1
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
11.如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )
A.45° B.55° C.60° D.75°
12.如图,菱形ABCD中,,点P从点B出发,沿折线方向移动,移动到点D停止.在形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
二.填空题
13.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.
14.在正方形ABCD中,E为BC上一点,EF⊥AC,EG⊥BD,垂足分别为F、G,如果AB=cm,那么EF+EG的长为______.
15.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________(只填写序号)
16.如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
17.对角线________的菱形是正方形,对角线________的矩形是正方形,
对角线________________的平行四边形是正方形,
对角线 的四边形是正方形.
18.如图所示,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以AE为边作第三个正方形AEGM,…已知正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3,…Sn(n为正整数),那么第8个正方形面积S8= .
三.解答题
19.如图,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.
20.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,且AF=CE.
(1)四边形ACEF是平行四边形吗?说明理由;
(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
21.如图,四边形是菱形,点、分别在边、的延长线上,且.连接、.
求证:.
22.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.
23.如图,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
24.如图①,在正方形ABCD中,E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是________,位置关系是________;
(2)如图②,若E,F分别是边CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请做出判断并给予证明;
(3)如图③,若E,F分别是边BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
25.如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形
26.如图,E是矩形ABCD的边BC的中点,P是边AD上的一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?并证明;
(2)在(1)的条件下,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?
北师大版九年级数学上册第一章1.3正方形的性质与判定 答案提示
一.选择题
1.菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
解:A.不正确,菱形的对角线不相等;
B.不正确,菱形的对角线不相等,矩形的对角线不垂直;
C.正确,三者均具有此性质;
D.不正确,矩形的四边不相等,菱形的四个角不相等;
故选C.
2.如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( )
A.1 B. C. D.
解:设CE=x,则BE=3-x,
由折叠性质可知,
EF=CE=x,DF=CD=AB=5
在Rt△DAF中,AD=3,DF=5,
∴AF=,
∴BF=AB-AF=5-4=1,
在Rt△BEF中,BE2+BF2=EF2,
即(3-x)2+12=x2,
解得x=,
故选:D.
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ) 选:B.
A.选①② B.选②③ C.选①③ D.选②④
4.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
解:由题意设CH=xcm,则DH=EH=(9﹣x)cm,
∵BE:EC=2:1,
∴CE=BC=3cm
∴在Rt△ECH中,EH2=EC2+CH2,
即(9﹣x)2=32+x2,
解得:x=4,即CH=4cm.故选:C.
5.若正方形的周长为40,则其对角线长为( )
A.100 B.20 C.10 D.10
解: ∵正方形的周长为40,∴正方形的边长为10,∴对角线长为10
故选C.
6.如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )选:B.
A.45° B.22.5° C.67.5° D.75°
下列说法不正确的是( )选:D.
A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形
8.如图,在菱形ABCD中,,,过菱形ABCD的对称中心O分别作边AB,BC的垂线,交各边于点E,F,G,H,则四边形EFGH的周长为( )
A. B. C. D.
解: ∵HF⊥BC,EG⊥AB,
∴∠BEO=∠BFO=90°,
∵∠A=120°,
∴∠B=60°,
∴∠EOF=120°,∠EOH=60°,
由菱形的对边平行,得HF⊥AD,EG⊥CD,
因为O点是菱形ABCD的对称中心,
∴O点到各边的距离相等,即OE=OF=OG=OH,
∴∠OEF=∠OFE=30°,∠OEH=∠OHE=60°,
∴∠HEF=∠EFG=∠FGH=∠EHG=90°,
所以四边形EFGH是矩形;
设OE=OF=OG=OH=x,
∴EG=HF=2x,,
如图,连接AC,则AC经过点O,
可得三角形ABC是等边三角形,
∴∠BAC=60°,AC=AB=2,
∴OA=1,∠AOE=30°,
∴AE=,
∴x=OE=
∴四边形EFGH的周长为EF+FG+GH+HE=,
故选A.
如图,正方形ABCD绕点A逆时针旋转45°与正方形AEFG重合,EF与CD交于点M,得四边形AEMD,正方形ABCD的边长为2,则两正方形重合部分(阴影部分)的面积为( )选:A.
A.4 -4 B.4 +4 C.8-4 D.+1
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )选:D.
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
11.如图,在正方形ABCD的外侧,作等边三角形ADE,连结BE交AD于点F,则∠DFE的度数为( )
A.45° B.55° C.60° D.75°
解: ∵四边形ABCD是正方形,
∴AB=AD,∠BAS=90°,
∵△AED是等边三角形,
∴∠AED=∠EAD=60°,AE=AD,
∴∠BAE=150°,AB=AE,
∴∠ABE=∠AEB=(180°-150°)=15°,
∴∠DFE=∠AFB=90°-15°=75°,
故选D.
12.如图,菱形ABCD中,,点P从点B出发,沿折线方向移动,移动到点D停止.在形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
解:连接AC,BD,如图所示.
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B.
∵∠B=60°,
∴∠D=∠B=60°.
∴和都是等边三角形.
点P在移动过程中,依次共有四个特殊位置:
(1)当点P移动到BC边的中点时,记作.
∵是等边三角形,是 BC的中点,
∴.
∴.
∴是直角三角形.
(2)当点P与点C重合时,记作.
此时,是等边三角形;
(3)当点P移动到CD边的中点时,记为.
∵和都是等边三角形,
∴.
∴是直角三角形.
(4)当点P与点D重合时,记作.
∵,
∴是等腰三角形.
综上,形状的变化过程中,依次出现的特殊三角形是:
直角三角形→等边三角形→直角三角形→等腰三角形.
故选:C
二.填空题
13.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是________.①③④
14.在正方形ABCD中,E为BC上一点,EF⊥AC,EG⊥BD,垂足分别为F、G,如果AB=cm,那么EF+EG的长为______.5cm;
15.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中错误的是_________(只填写序号) ②③或①④
解: 有6种选法:(1)①②:由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(2)②③:由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误;
(3)①③:由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确;
(4)②④:由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
(5)①④:由①得有一组邻边相等的平行四边形是菱形,由④得对角线互相垂直的平行四边形是菱形,所以不能得出平行四边形ABCD是正方形,错误;
(6)③④:由③得对角线相等的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确;
综上所述:错误的是:②③或①④;
故答案为:②③或①④.
16.如图,菱形的对角线、相交于点O,,垂足为E,,,则的长为______.
解:∵菱形ABCD的对角线AC、BD相交于点O,且AC=8,DB=6,
∴AO=4,DO=3,∠AOD=90°,
∴AD=5,
在 中,由等面积法得: ,
∴
故答案为: .
17.对角线________的菱形是正方形,对角线________的矩形是正方形,
对角线________________的平行四边形是正方形,
对角线 的四边形是正方形.
相等 互相垂直 互相垂直且相等 互相垂直平分且相等
18.如图所示,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以AE为边作第三个正方形AEGM,…已知正方形ABCD的面积S1=1,按上述方法所作的正方形的面积依次为S2,S3,…Sn(n为正整数),那么第8个正方形面积S8= .
解:根据题意可得:第n个正方形的边长是第(n﹣1)个的倍;故面积是第(n﹣1)个的2倍,已知第一个面积为1;则那么第8个正方形面积S8=27=128.
故答案为128.
三.解答题
19.如图,四边形ABCD是正方形,E,F分别是AB,AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.
证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBE=90°.
∵BF⊥CE,∴∠BCE+∠CBG=90°.
∵∠ABF+∠CBG=90°,∴∠BCE=∠ABF.
在△BCE和△ABF中,
∠BCE=∠ABF,BC=AB,∠CBE=∠A,
∴△BCE≌△ABF(ASA),∴AF=BE.
20.如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于点D,交AB于点E,点F在DE的延长线上,且AF=CE.
(1)四边形ACEF是平行四边形吗?说明理由;
(2)当∠B的大小满足什么条件时,四边形ACEF为菱形?请说明你的结论;
(3)四边形ACEF有可能是正方形吗?为什么?
解:(1)四边形ACEF是平行四边形;
理由:∵DE垂直平分BC,
∴D为BC的中点,ED⊥BC,
又∵AC⊥BC,
∴ED∥AC,
∴E为AB中点,
∴ED是△ABC的中位线.
∴BE=AE,FD∥AC.
∴BD=CD,
∴Rt△ABC中,CE是斜边AB的中线,
∴CE=AE=AF.
∴∠F=∠5=∠1=∠2.
∴∠FAE=∠AEC.
∴AF∥EC.
又∵AF=EC,
∴四边形ACEF是平行四边形;
(2)理由:∵∠ACB=90°,∠B=30°,
∴AC=AB,
由(1)知CE=AB,∴AC=CE
又四边形ACEF为平行四边形
∴四边形ACEF为菱形;
解:(3)四边形ACEF不可能是正方形,
∵∠ACB=90°,
∴∠ACE<∠ACB,
即∠ACE<90°,不能为直角,
所以四边形ACEF不可能是正方形
21.如图,四边形是菱形,点、分别在边、的延长线上,且.连接、.
求证:.
解:∵四边形ABCD是菱形,
∴BC=CD,∠ADC=∠ABC,
∴∠CDF=∠CBE,
在△BEC和△DFC中,
,
∴△BEC≌△DFC(SAS),
∴CE=CF.
22.如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
又E、F分别是边AB、CD的中点,
∴DF=BE,
又AB∥CD,
∴四边形DEBF是平行四边形,
∴DE=BF.
23.如图,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
证明:∵四边形ABCD和四边形CEFG是正方形,∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,∴∠ADH=∠HGF=∠E=∠B=90°.又∵DH=CE,BK=CE,∴BK=GF=DH=EF,KE=GH=AB=AD,∴△ABK≌△KEF≌△HGF≌△ADH,∴AK=KF=HF=AH,∠BAK=∠DAH.∵∠BAD=90°,∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,∴四边形AKFH为正方形.
24.如图①,在正方形ABCD中,E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是________,位置关系是________;
(2)如图②,若E,F分别是边CB,BA延长线上的点,其他条件不变,(1)中结论是否仍然成立?请做出判断并给予证明;
(3)如图③,若E,F分别是边BC,AB延长线上的点,其他条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
解:(1)相等 互相平行
(2)成立.
证明:如图,过点G作GH⊥CB交其延长线于点H.
∵EG⊥DE,
∴∠GEH+∠DEC=90°.
∵∠GEH+∠HGE=90°,
∴∠DEC=∠HGE.
在△HGE与△CED中,
∠GHE=∠DCE=90°,∠HGE=∠DEC,EG=DE,
∴△HGE≌△CED,∴GH=CE,HE=CD.
∵CE=BF,∴GH=BF.
又∵GH∥BF且∠GHE=90°,
∴四边形GHBF是矩形,
∴FG=BH,FG∥CH,∴FG∥CE.
∵四边形ABCD是正方形,∴CD=BC,
∴HE=BC,
∴HE+EB=BC+EB,
∴BH=CE,∴FG=CE.
(3)成立.FG=CE,FG∥CE.
25.如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形
解:∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵∠DCE=90°,∴∠ACD+∠ACE=90°,
∴∠BCD=∠ACE,
在△CBD与△CAE中,
CB=CA
∠BCD=∠ACE
CD=CE
∴△CBD≌△CAE(SAS),
∴∠B=∠CAE,
∵∠B+∠BAC=90°,∴∠BAC+∠EAC=90°,∴AB⊥AE;
解: (2)证明:∵点D为AB中点,
∴∠ADC=90°,
∵∠DCE=90°,∠BAE=90°,
∴四边形ADCE是矩形,
∴CD=CE,∴四边形ADCE是正方形
26.如图,E是矩形ABCD的边BC的中点,P是边AD上的一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?并证明;
(2)在(1)的条件下,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?
解:(1)当矩形ABCD的长是宽的2倍时,四边形PHEF是矩形.
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
∵E是BC的中点,
∴AB=BE=EC=CD,则△ABE,△DCE均是等腰直角三角形,
∴∠AEB=∠DEC=45°,
∴∠AED=90°.
在四边形PHEF中,∵∠PFE=∠FEH=∠EHP=90°,
∴四边形PHEF是矩形.
(2)当点P是AD的中点时,矩形PHEF变为正方形.理由如下:
由(1)可得∠BAE=∠CDE=45°,
∴∠FAP=∠HDP=45°.
又∵∠AFP=∠DHP=90°,AP=DP,
∴Rt△AFP≌Rt△DHP,
∴PF=PH,
∴矩形PHEF是正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
