2022—2023学年沪科版数学九年级上册 22.1比例线段 同步练习(word版 含答案)
文档属性
| 名称 | 2022—2023学年沪科版数学九年级上册 22.1比例线段 同步练习(word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览



文档简介
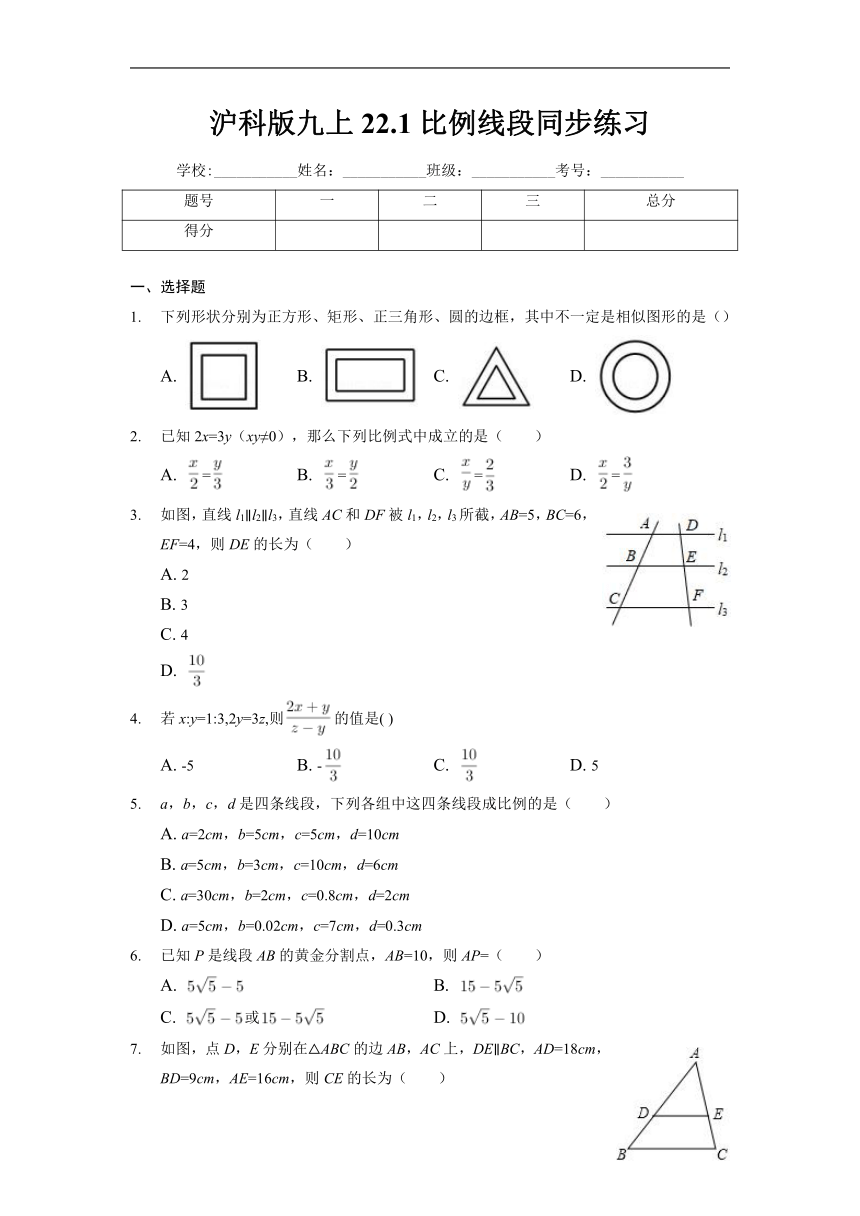
沪科版九上22.1比例线段同步练习
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一、选择题
下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是()
A. B. C. D.
已知2x=3y(xy≠0),那么下列比例式中成立的是( )
A. = B. = C. = D. =
如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为( )
A. 2
B. 3
C. 4
D.
若x:y=1:3,2y=3z,则的值是( )
A. -5 B. - C. D. 5
a,b,c,d是四条线段,下列各组中这四条线段成比例的是( )
A. a=2cm,b=5cm,c=5cm,d=10cm
B. a=5cm,b=3cm,c=10cm,d=6cm
C. a=30cm,b=2cm,c=0.8cm,d=2cm
D. a=5cm,b=0.02cm,c=7cm,d=0.3cm
已知P是线段AB的黄金分割点,AB=10,则AP=( )
A. B.
C. 或 D.
如图,点D,E分别在△ABC的边AB,AC上,DE∥BC,AD=18cm,BD=9cm,AE=16cm,则CE的长为( )
A. 16cm
B. 8cm
C. 24cm
D. 12cm
如图,在山西旅游景区地图上,图上距离与实际距离之比约1:10000000,若从太原到大同云冈石窟所在地的实际距离约为251.0km,则这两地的图上距离约为( )cm.
A. 0.251 B. 2.51 C. 25.1 D. 251
勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.在设计人体雕像时,使雕像的下部(腰以下)与全部(全身)的高度比值接近0.618,可以增加视觉美感.如图,如果雕像的高为2m,那么它的下部应设计为(结果保留两位小数)( )
A. 1.23m B. 1.24m C. 1.25m D. 1.26m
如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A. 4.4
B. 4
C. 3.4
D. 2.4
二、填空题
已知线段AB=2,C是线段AB的黄金分割点,且AC<CB,则AC的长度为______.
已知点M、N在线段AB上,=,=,且MN=2,则AB=______
如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B=______.
四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,则a=______cm.
已知线段AB=6cm,点C是线段AB的黄金分割点,且AC>BC,则BC=______cm.
三、解答题
已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
(1)若.求代数式的值;
(2)已知,求代数式的值.
(1)已知a=4.5,b=2,c是a,b的比例中项,求c.
(2)如图,C是AB的黄金分割点,且AC>BC,AB=4,求AC的长.
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)若AD=5,DB=6,EC=12,求AE的长;
(2)若AB=10,AD=4,AE=6,求EC的长.
已知,如图l1∥l2∥l3,AB=3,BC=5,DF=16,求DE和EF的长.
如图,在RtABC中,ACB=,CD是斜边AB上的高,AC=3,BC=4.
(1)求CD和AD的长.
(2)求证:AC是AD和AB的比例中项.
1.B
2.B
3.D
4.A
5.B
6.C
7.B
8.B
9.B
10.D
11.3-.
12.
13.65°
14.1
15.(9-3)
16.解:(1)∵a=0.3m=30cm;b=60cm,
∴a:b=30:60=1:2;
(2)∵线段a、b、c、d是成比例线段,
∴=,
∵c=12dm=120cm,
∴=,
∴d=240cm;
(3)是,理由:
∵b2=3600,ac=30×120=3600,
∴b2=ac,
∴b是a和c的比例中项.
17.解:(1)∵,
∴
=-2
=-2
=;
(2)设===k,
∴a=2k,b=3k,c=5k,
∴
=
=
=.
18.解:(1)∵c是 a,b的比例中项,
∴c2=ab=4.5×2=9,
∴c1=3,c2=-3,
∴c为3或-3;
(2)∵C是AB的黄金分割点,且AC>BC,AB=4,
∴AC=AB=×4=2-2.
19.解:(1)∵DE∥BC,
∴=,即=,
解得,AE=10;
(2)DE∥BC,
∴=,即=,
解得,AC=15,
∴EC=AC-AE=9.
20.解:∵l1∥l2∥l3,
∴AB:BC=DE:EF,
∵AB=3,BC=5,DF=16,
∴3:5=DE:(16-DE),
∴DE=6,
∴EF=16-6=10.
21.解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=,
∵S△ABC=AC BC=AB CD,
∴CD==,
在Rt△ACD中,AD==
(2)∵AD·AB=,
AC2=9,
∴AC2=AD AB,
∴AC是AD和AB的比例中项.
第2页,共7页
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
一、选择题
下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是()
A. B. C. D.
已知2x=3y(xy≠0),那么下列比例式中成立的是( )
A. = B. = C. = D. =
如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为( )
A. 2
B. 3
C. 4
D.
若x:y=1:3,2y=3z,则的值是( )
A. -5 B. - C. D. 5
a,b,c,d是四条线段,下列各组中这四条线段成比例的是( )
A. a=2cm,b=5cm,c=5cm,d=10cm
B. a=5cm,b=3cm,c=10cm,d=6cm
C. a=30cm,b=2cm,c=0.8cm,d=2cm
D. a=5cm,b=0.02cm,c=7cm,d=0.3cm
已知P是线段AB的黄金分割点,AB=10,则AP=( )
A. B.
C. 或 D.
如图,点D,E分别在△ABC的边AB,AC上,DE∥BC,AD=18cm,BD=9cm,AE=16cm,则CE的长为( )
A. 16cm
B. 8cm
C. 24cm
D. 12cm
如图,在山西旅游景区地图上,图上距离与实际距离之比约1:10000000,若从太原到大同云冈石窟所在地的实际距离约为251.0km,则这两地的图上距离约为( )cm.
A. 0.251 B. 2.51 C. 25.1 D. 251
勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.在设计人体雕像时,使雕像的下部(腰以下)与全部(全身)的高度比值接近0.618,可以增加视觉美感.如图,如果雕像的高为2m,那么它的下部应设计为(结果保留两位小数)( )
A. 1.23m B. 1.24m C. 1.25m D. 1.26m
如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=1.5,BC=2,DE=1.8,则EF=( )
A. 4.4
B. 4
C. 3.4
D. 2.4
二、填空题
已知线段AB=2,C是线段AB的黄金分割点,且AC<CB,则AC的长度为______.
已知点M、N在线段AB上,=,=,且MN=2,则AB=______
如图,四边形ABCD∽四边形EFGH,∠E=85°,∠G=90°,∠D=120°,则∠B=______.
四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,则a=______cm.
已知线段AB=6cm,点C是线段AB的黄金分割点,且AC>BC,则BC=______cm.
三、解答题
已知线段a=0.3m,b=60cm,c=12dm.
(1)求线段a与线段b的比.
(2)如果线段a、b、c、d成比例,求线段d的长.
(3)b是a和c的比例中项吗?为什么?
(1)若.求代数式的值;
(2)已知,求代数式的值.
(1)已知a=4.5,b=2,c是a,b的比例中项,求c.
(2)如图,C是AB的黄金分割点,且AC>BC,AB=4,求AC的长.
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)若AD=5,DB=6,EC=12,求AE的长;
(2)若AB=10,AD=4,AE=6,求EC的长.
已知,如图l1∥l2∥l3,AB=3,BC=5,DF=16,求DE和EF的长.
如图,在RtABC中,ACB=,CD是斜边AB上的高,AC=3,BC=4.
(1)求CD和AD的长.
(2)求证:AC是AD和AB的比例中项.
1.B
2.B
3.D
4.A
5.B
6.C
7.B
8.B
9.B
10.D
11.3-.
12.
13.65°
14.1
15.(9-3)
16.解:(1)∵a=0.3m=30cm;b=60cm,
∴a:b=30:60=1:2;
(2)∵线段a、b、c、d是成比例线段,
∴=,
∵c=12dm=120cm,
∴=,
∴d=240cm;
(3)是,理由:
∵b2=3600,ac=30×120=3600,
∴b2=ac,
∴b是a和c的比例中项.
17.解:(1)∵,
∴
=-2
=-2
=;
(2)设===k,
∴a=2k,b=3k,c=5k,
∴
=
=
=.
18.解:(1)∵c是 a,b的比例中项,
∴c2=ab=4.5×2=9,
∴c1=3,c2=-3,
∴c为3或-3;
(2)∵C是AB的黄金分割点,且AC>BC,AB=4,
∴AC=AB=×4=2-2.
19.解:(1)∵DE∥BC,
∴=,即=,
解得,AE=10;
(2)DE∥BC,
∴=,即=,
解得,AC=15,
∴EC=AC-AE=9.
20.解:∵l1∥l2∥l3,
∴AB:BC=DE:EF,
∵AB=3,BC=5,DF=16,
∴3:5=DE:(16-DE),
∴DE=6,
∴EF=16-6=10.
21.解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=,
∵S△ABC=AC BC=AB CD,
∴CD==,
在Rt△ACD中,AD==
(2)∵AD·AB=,
AC2=9,
∴AC2=AD AB,
∴AC是AD和AB的比例中项.
第2页,共7页
