人教版八年级数学上册 11.2与三角形有关的角 达标测试题(word版,含解析)
文档属性
| 名称 | 人教版八年级数学上册 11.2与三角形有关的角 达标测试题(word版,含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 360.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览



文档简介
2022-2023学年人教版八年级数学上册《11.2与三角形有关的角》达标测试题(附答案)
一.选择题(共8小题,满分40分)
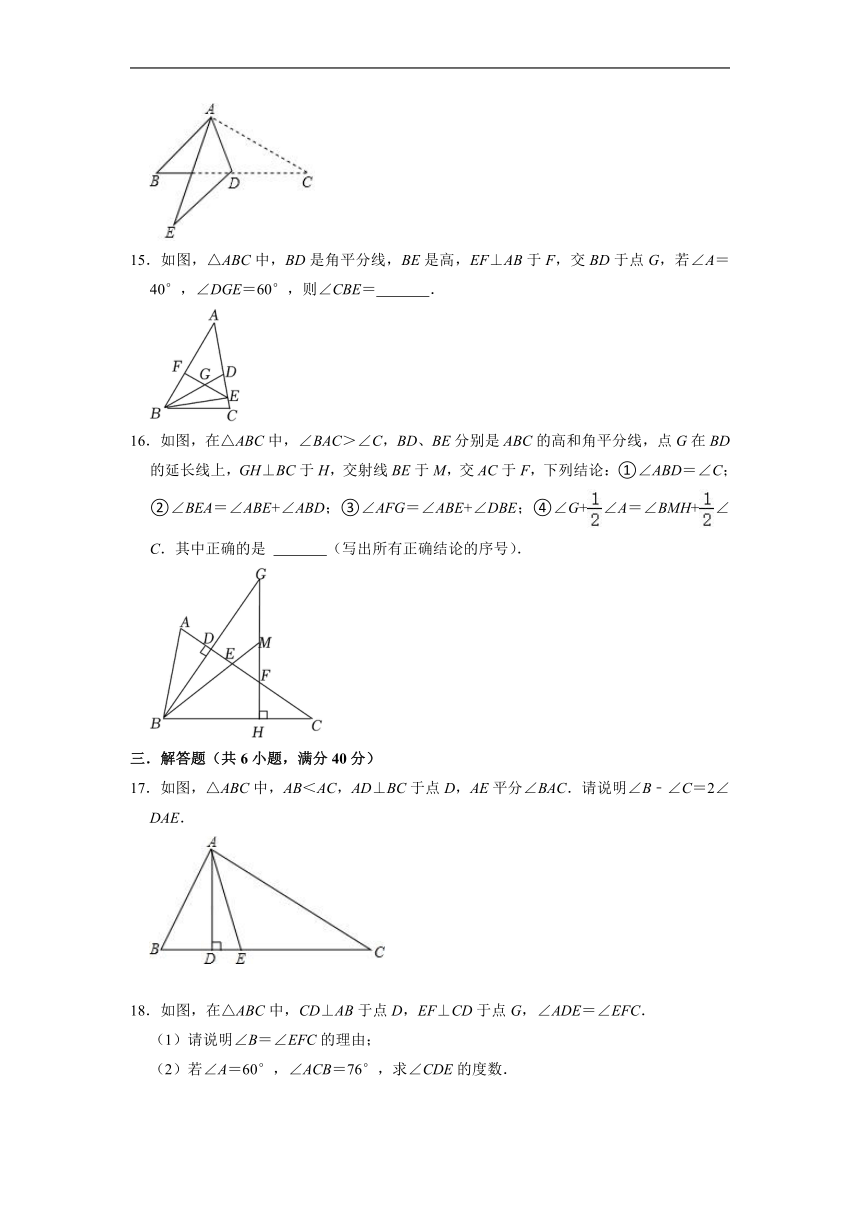
1.在直角三角形ABC中,∠1=30°,在C点处作AB的平行线,如图所示,则∠2的度数是( )
A.50° B.45° C.60° D.30°
2.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若∠BDE=56°,则∠DAE的度数为( )度.
A.23 B.28 C.52 D.56
3.如图,△ABC沿直线MN折叠,使点A与AB边上的点E重合,若∠B=54°,∠C=90°,则∠ENC等于( )
A.54° B.62° C.72° D.76°
4.如图,∠B=30°,∠CAD=65°且AD平分∠CAE,则∠ACD等于( )
A.95° B.65° C.50° D.80°
5.如图,线段AB、CD相交于点O,连接AD、CB,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A.∠P=2(∠B﹣∠D) B.
C. D.
6.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
7.三角形是一种常见且神奇的图形,我们小学阶段就知道,三角形的内角和等于180°.如图,ABC的角平分线BE、CD相交于点F,∠A=90°,GD∥BC,BG⊥GD于点G,下列结论:①∠CBG=90°;②∠BDG=2∠ABE;③∠BFD=∠FBC+∠FCB;④∠AEB=∠EBG;⑤∠CFE=45°,其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
8.如图,在△ABC中,∠A=52°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,同理可得∠A3,则∠A3=( )度.
A.26° B.15° C.10° D.6.5°
二.填空题(共8小题,满分40分)
9.已知在△ABC中,∠A=114°,∠B=∠C,则∠B= .
10.如图,在△ABC中,∠A=65°,则∠1+∠2= °.
11.如图,在△ABC中,AD是BAC的平分线,EF∥AD,交BC于E、AB于F、CA的延长线于G,∠B=30°,∠C=70°,则∠G的度数 .
12.如图,在△ABC中,∠B=80°,∠C=42°,AD⊥BC于点D,AE平分∠BAC,则∠DAE= .
13.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为 °.
14.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若∠BAE=50°,则∠DAC的度数为 °.
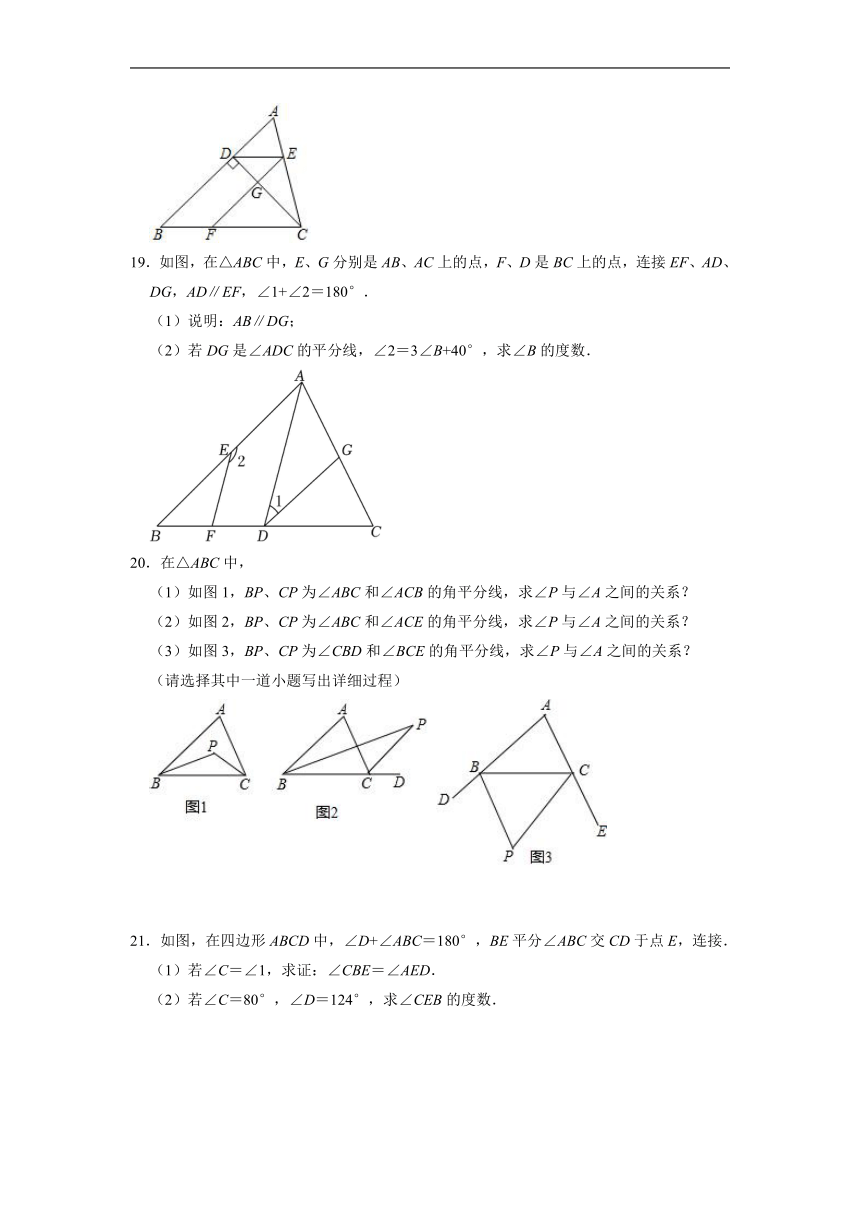
15.如图,△ABC中,BD是角平分线,BE是高,EF⊥AB于F,交BD于点G,若∠A=40°,∠DGE=60°,则∠CBE= .
16.如图,在△ABC中,∠BAC>∠C,BD、BE分别是ABC的高和角平分线,点G在BD的延长线上,GH⊥BC于H,交射线BE于M,交AC于F,下列结论:①∠ABD=∠C;②∠BEA=∠ABE+∠ABD;③∠AFG=∠ABE+∠DBE;④∠G+∠A=∠BMH+∠C.其中正确的是 (写出所有正确结论的序号).
三.解答题(共6小题,满分40分)
17.如图,△ABC中,AB<AC,AD⊥BC于点D,AE平分∠BAC.请说明∠B﹣∠C=2∠DAE.
18.如图,在△ABC中,CD⊥AB于点D,EF⊥CD于点G,∠ADE=∠EFC.
(1)请说明∠B=∠EFC的理由;
(2)若∠A=60°,∠ACB=76°,求∠CDE的度数.
19.如图,在△ABC中,E、G分别是AB、AC上的点,F、D是BC上的点,连接EF、AD、DG,AD∥EF,∠1+∠2=180°.
(1)说明:AB∥DG;
(2)若DG是∠ADC的平分线,∠2=3∠B+40°,求∠B的度数.
20.在△ABC中,
(1)如图1,BP、CP为∠ABC和∠ACB的角平分线,求∠P与∠A之间的关系?
(2)如图2,BP、CP为∠ABC和∠ACE的角平分线,求∠P与∠A之间的关系?
(3)如图3,BP、CP为∠CBD和∠BCE的角平分线,求∠P与∠A之间的关系?
(请选择其中一道小题写出详细过程)
21.如图,在四边形ABCD中,∠D+∠ABC=180°,BE平分∠ABC交CD于点E,连接.
(1)若∠C=∠1,求证:∠CBE=∠AED.
(2)若∠C=80°,∠D=124°,求∠CEB的度数.
22.如图1至图2,在△ABC中,∠BAC=α,点D在边AC上,作DE垂直于直线BC,垂足为点E,BM为△ABC的角平分线,∠ADE的平分线交直线BC于点G.
特例感悟:
(1)如图1,延长AB交DG于点F,若BM∥DG,∠F=30°.
解决问题:
①∠ABC= °;
②求证:AB⊥AC.
深入探究:
(2)如图2,当0°<α<90°,DG与BM反向延长线交于点H,用含α的代数式表示∠BHD,并说明理由;
拓展延伸:
(3)当点D在边AC上移动时,若射线DG与线段BM相交,设交点为N,则∠BND与α的关系式是 .
参考答案
一.选择题(共8小题,满分40分)
1.解:在Rt△ABC中,∠ACB=90°,∠1=30°,
则∠ABC=90°﹣∠1=60°,
∵a∥b,
∴∠2=∠ABC=60°,
故选:C.
2.解:∵∠C=90°,
∴∠CAB+∠B=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE+∠B=90°,
∴∠CAB=∠BDE,
∵∠BDE=56°,
∴∠CAB=56°,
∵AD平分∠CAB,
∴∠DAE=∠CAB=28°,
故选:B.
3.解:∵∠B=54°,∠C=90°,
∴∠A=90°﹣54°=36°,
由折叠的性质可知,∠NEA=∠A=36°,
∴∠ENC=∠NEA+∠A=72°,
故选:C.
4.解:∵∠CAD=65°,AD平分∠CAE,
∴∠CAE=2∠CAD=130°,
∴∠BAC=180°﹣130°=50°,
∵∠B=30°,
∴∠ACD=∠B+∠BAC=30°+50°=80°.
故选:D.
5.解:∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
∵∠D+∠DAP=∠P+∠DCP①,
∠PAB+∠P=∠B+∠PCB②,
∴①﹣②得:∠D﹣∠P=∠P﹣∠B,
∴2∠P=∠D+∠B,
即∠P=(∠D+∠B).
故选:B.
6.解:在△FBC中,∠BFC=125°.
∴∠FBC+∠FCB=180°﹣∠BFC=55°.
∵BF平分∠ABC,CF平分∠ACB.
∴∠ABC=2∠FBC,∠ACB=2∠FCB.
∴∠ABC+∠ACB=2(∠FBC+∠FCB)=110°.
∴在△ABC中,∠A=180°﹣(∠ABC+∠ACB)=70°.
故选:C.
7.解:①∵BG⊥GD于点G,
∴∠G=90°.
∵GD∥BC,
∴∠G+∠GBC=180°.
∴∠GBC=180°﹣∠G=90°.
故①正确.
②∵GD∥BC,
∴∠GDB=∠DBC.
∵BE平分∠ABC,
∴∠ABC=2∠ABE.
∴∠GDB=2∠ABE.
故②正确.
③根据三角形外角的性质,得∠BFD=∠FBC+∠FCB,故③正确.
④由①知,∠GBC=∠GBF+∠FBC=90°.
∴∠EBG=90°﹣∠FBC.
∵∠AEB=∠ACB+∠EBC,
∴∠AEB=∠ABC﹣∠ABE+∠EBC.
∵∠A=90°,
∴∠ABC+∠ABC=180°﹣∠A=90°.
∴∠AEB=90°﹣∠ABE.
∵∵BE平分∠ABC,
∴∠ABE=∠EBC.
∴∠AEB=∠EBG.
故④正确.
⑤由④得,∠ABC+∠ACB=90°.
∵BE平分∠ABC,CD平分∠ACB,
∴∠EBC=,∠DCB=.
∴∠EBC+∠DCB=.
∴∠CFE=∠EBC+∠FCB=45°.
故⑤正确.
综上:正确的有①②③④⑤,共5个.
故选:A.
8.解:∵∠BA1是∠ABC的平分线,CA1是∠ACD和∠ACD的平分线,
∴∠ABA1=∠A1BC=∠ABC,∠ACA1=∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∴∠A1=∠A,
同理可得,∠A2=∠A1,∠A3=∠A2,
∴∠A3=∠A=×52°=6.5°,
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵∠A=114°,∠B=∠C,
∴114°+∠B+∠C=180°,
∴∠B=33°,
故答案为:33°.
10.解:∵△ABC中,∠A=65°,
∴∠B+∠C=180°﹣65°=115°,
∵∠B+∠C+∠1+∠2=360°,
∴∠1+∠2=360°﹣115°=245°,
故答案为:245.
11.解:∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°.
∵AD平分∠BAC,
∴∠DAC==40°.
∵EF∥AD,
∴∠G=∠DAC=40°.
故答案为:40°.
12.解:在△ABC中,∠B=80°,∠C=42°,
∴∠BAC=180°﹣∠B﹣∠C=58°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣42°=48°,
∴∠DAE=∠DAC﹣∠EAC=48°﹣29°=19°,
故答案为:19°.
13.解:∵∠B=50°,∠CEB=∠ADB﹣90°,
∴∠EHD=180°﹣50°=130°,
又∵∠EHD=∠AHC,
∴∠AHC=130°,
故答案为:130.
14.解:∵∠B=40°,∠C=30°,
∴∠BAC=110°,
∵∠BAE=50°,
∴∠CAE=60°,
∵△ADC沿直线AD折叠得到△ADE,
∴∠CAD=∠EAD=30°,
故答案为:30.
15.解:∵EF⊥AB,
∴∠AFE=90°,
∴∠A+∠AEF=90°,
∵∠A=40°,
∴∠AEF=50°,
∵∠AEF+∠DGE+∠GDE=180°,∠DGE=60°,
∴∠GDE=180°﹣50°﹣60°=70°,
∴∠ABD=∠GDE﹣∠A=70°﹣40°=30°,
∵BD是角平分线,
∴∠ABC=2∠ABD=60°,
∵BE是△ABC的高线,
∴BE⊥AC,
∴∠ABE+∠A=90°,
∴∠ABE=90°﹣40°=50°,
∴∠CBE=ABC﹣∠ABE=60°﹣50°=10°.
故答案为:10°.
16.解:①∵GH⊥BC,BG⊥AC,
∴∠BDC=∠BHG=90°,
∴∠G+∠GBH=∠DBC+∠C=90°,
∴∠G=∠C,
若∠ABD=∠C,则∠ABD=∠G,
则有AB∥GH,而已知条件并不能对此证明,
因此①错误.
②∵∠BEA=∠EBC+∠C,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠BEA=∠ABE+∠C,
由于①不能证明,故②也不能证明.
③显然,∠AFG=∠HFC (对顶角),
∵GH⊥BC,BG⊥AC,
∴∠FHC=∠BDC=90°,
∴∠HFC+∠C=90°,∠DBC+∠C=90°,
∴∠HFC=∠DBC=∠DBE+∠EBC,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠HFC=∠DBC=∠DBE+∠EBC=∠ABE+∠DBE,
因此,∠AFG=∠HFC=∠ABE+∠DBE,③正确.
④∵BG⊥AC,
∴∠ADB=∠BDC=90°,
∴∠A+∠ABD=∠DBC+∠C=90°,
∴∠A﹣∠C=∠DBC﹣∠ABD=∠DBE+∠EBC﹣∠ABD,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠A﹣∠C=∠DBE+∠ABE﹣∠ABD=2∠DBE,
又∵∠BMH=∠DBE+∠G,
∴∠BMH=(∠A﹣∠C)+∠G,
即∠G+∠A=∠BMH+∠C,
故④正确,
故答案为:③④.
三.解答题(共6小题,满分40分)
17.解:∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC,
∵AD⊥BC,
∴∠ADE=90°,
即∠DAE+∠AED=90°,
而∠AED=∠C+∠CAE,
∴∠DAE+∠C+=90°,
∴2∠DAE+2∠C+∠BAC=180°,
即2∠DAE=180°﹣2∠C﹣∠BAC=∠B﹣∠C.
18.(1)证明:∵CD⊥AB于点D,EF⊥CD于点G,
∴AB∥EF,
∴∠B=∠EFC;
(2)解:∵∠A=60°,∠ACB=76°,
∴∠B=44°,
∵CD⊥AB,
∴∠BCD=90°﹣∠B=46°,
∵AB∥EF,
∴∠ADE=∠DEF,
∵∠ADE=∠EFC,
∴∠DEF=∠EFC,
∴DE∥BC,
∴∠CDE=∠BCD,
∴∠CDE=46°.
19.证明:(1)由题意可知,
∠BEF=∠1,∠BFE=∠ADB,
∴∠BEF+∠BFE=∠1+ADB,
∴180°﹣(∠BEF+∠BFE)=180°﹣(∠1+ADB),
即∠B=∠GDC,
∴AB∥DG.
解:(2)∵DG是∠ADC的平分线,且AB∥DG,
∴∠1=∠DGC=∠B,
∵∠2=3∠B+40°,
∴180°﹣∠1=3∠B+40°,
∴180°﹣∠B=3∠B+40°,
∴∠B=35°.
20.解:(1)∵BP、CP为∠ABC和∠ACB的角平分线,
∴∠CBP=,∠BCP=.
∴∠CBP+∠CBP=.
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A.
∴∠PBC+∠PCB=.
∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣=90°+.
(2)∵∠P+∠PBC=∠PCD,
∴∠P=∠PCD﹣∠PBC.
∵BP、CP为∠ABC和∠ACE的角平分线,
∴∠PCD=,∠PBC=.
∴∠P==.
(3)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A.
∵BP、CP为∠CBD和∠BCE的角平分线,
∴∠CBP=,∠BCP=.
∴=.
∴∠P=180°﹣(∠CBP+∠BCP)=180°﹣=90°﹣.
21.(1)证明:∵∠C+∠CBE+∠CEB=180°,∠AED+∠1+∠CEB=180°,∠C=∠1,
∴∠CBE=∠AED;
(2)解:∵∠D+∠ABC=180°,∠D=124°,
∴∠ABC=56°,
∵BE平分∠ABC,
∴∠CBE=∠ABC=28°,
∵∠C+∠CBE+∠CEB=180°,∠C=80°,
∴∠CEB=72°.
22.解:(1)①∵BM∥DG,
∴∠ABM=∠F=30°,
∵BM为△ABC的角平分线,
∴∠ABC=2∠ABM=60°,
故答案为:60°;
②证明:由①得,∠CBM=∠ABM=30°,
∵BM∥DG,
∴∠DGC=∠CBM=30°,
∵DE⊥BC,
∴∠EDG=60°,
∵DG平分∠ADE,
∴∠ADF=60°,
∴∠A=180°﹣30°﹣60°=90°,
∴AC⊥AB;
(2)45°﹣.
理由:由八字模型可得,△BHG和△DEG中,
∠BHD=∠EDG+90°﹣∠HBG=∠ADE+90°﹣(180°﹣ABC)=(∠ADE+∠ABC)﹣90°=45°﹣.
故答案为:45°﹣;
(3)①如图,
由八字模型可得,△ABM和△NMD中,
∠BND=∠ABN+∠A﹣∠MDN=∠ABC+α﹣(90°﹣∠ACB)=(∠ABC+∠ACB)+α﹣45°=45°+;
②如图,
由四边形的内角和得,
∠BND=360°﹣90°﹣ABC﹣ADE=270°﹣(270°﹣α)=135°+;
③如图,
由八字模型可得,∠BND+∠ABM=∠ADG+∠DAB,
∴∠BND=∠ADE+(180°﹣α)﹣ABC=(90°﹣∠ACB)+(180°﹣α)﹣ABC=135°﹣;
综上,∠BND=45°+或135°±.
一.选择题(共8小题,满分40分)
1.在直角三角形ABC中,∠1=30°,在C点处作AB的平行线,如图所示,则∠2的度数是( )
A.50° B.45° C.60° D.30°
2.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若∠BDE=56°,则∠DAE的度数为( )度.
A.23 B.28 C.52 D.56
3.如图,△ABC沿直线MN折叠,使点A与AB边上的点E重合,若∠B=54°,∠C=90°,则∠ENC等于( )
A.54° B.62° C.72° D.76°
4.如图,∠B=30°,∠CAD=65°且AD平分∠CAE,则∠ACD等于( )
A.95° B.65° C.50° D.80°
5.如图,线段AB、CD相交于点O,连接AD、CB,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A.∠P=2(∠B﹣∠D) B.
C. D.
6.如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
7.三角形是一种常见且神奇的图形,我们小学阶段就知道,三角形的内角和等于180°.如图,ABC的角平分线BE、CD相交于点F,∠A=90°,GD∥BC,BG⊥GD于点G,下列结论:①∠CBG=90°;②∠BDG=2∠ABE;③∠BFD=∠FBC+∠FCB;④∠AEB=∠EBG;⑤∠CFE=45°,其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
8.如图,在△ABC中,∠A=52°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2,同理可得∠A3,则∠A3=( )度.
A.26° B.15° C.10° D.6.5°
二.填空题(共8小题,满分40分)
9.已知在△ABC中,∠A=114°,∠B=∠C,则∠B= .
10.如图,在△ABC中,∠A=65°,则∠1+∠2= °.
11.如图,在△ABC中,AD是BAC的平分线,EF∥AD,交BC于E、AB于F、CA的延长线于G,∠B=30°,∠C=70°,则∠G的度数 .
12.如图,在△ABC中,∠B=80°,∠C=42°,AD⊥BC于点D,AE平分∠BAC,则∠DAE= .
13.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为 °.
14.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若∠BAE=50°,则∠DAC的度数为 °.
15.如图,△ABC中,BD是角平分线,BE是高,EF⊥AB于F,交BD于点G,若∠A=40°,∠DGE=60°,则∠CBE= .
16.如图,在△ABC中,∠BAC>∠C,BD、BE分别是ABC的高和角平分线,点G在BD的延长线上,GH⊥BC于H,交射线BE于M,交AC于F,下列结论:①∠ABD=∠C;②∠BEA=∠ABE+∠ABD;③∠AFG=∠ABE+∠DBE;④∠G+∠A=∠BMH+∠C.其中正确的是 (写出所有正确结论的序号).
三.解答题(共6小题,满分40分)
17.如图,△ABC中,AB<AC,AD⊥BC于点D,AE平分∠BAC.请说明∠B﹣∠C=2∠DAE.
18.如图,在△ABC中,CD⊥AB于点D,EF⊥CD于点G,∠ADE=∠EFC.
(1)请说明∠B=∠EFC的理由;
(2)若∠A=60°,∠ACB=76°,求∠CDE的度数.
19.如图,在△ABC中,E、G分别是AB、AC上的点,F、D是BC上的点,连接EF、AD、DG,AD∥EF,∠1+∠2=180°.
(1)说明:AB∥DG;
(2)若DG是∠ADC的平分线,∠2=3∠B+40°,求∠B的度数.
20.在△ABC中,
(1)如图1,BP、CP为∠ABC和∠ACB的角平分线,求∠P与∠A之间的关系?
(2)如图2,BP、CP为∠ABC和∠ACE的角平分线,求∠P与∠A之间的关系?
(3)如图3,BP、CP为∠CBD和∠BCE的角平分线,求∠P与∠A之间的关系?
(请选择其中一道小题写出详细过程)
21.如图,在四边形ABCD中,∠D+∠ABC=180°,BE平分∠ABC交CD于点E,连接.
(1)若∠C=∠1,求证:∠CBE=∠AED.
(2)若∠C=80°,∠D=124°,求∠CEB的度数.
22.如图1至图2,在△ABC中,∠BAC=α,点D在边AC上,作DE垂直于直线BC,垂足为点E,BM为△ABC的角平分线,∠ADE的平分线交直线BC于点G.
特例感悟:
(1)如图1,延长AB交DG于点F,若BM∥DG,∠F=30°.
解决问题:
①∠ABC= °;
②求证:AB⊥AC.
深入探究:
(2)如图2,当0°<α<90°,DG与BM反向延长线交于点H,用含α的代数式表示∠BHD,并说明理由;
拓展延伸:
(3)当点D在边AC上移动时,若射线DG与线段BM相交,设交点为N,则∠BND与α的关系式是 .
参考答案
一.选择题(共8小题,满分40分)
1.解:在Rt△ABC中,∠ACB=90°,∠1=30°,
则∠ABC=90°﹣∠1=60°,
∵a∥b,
∴∠2=∠ABC=60°,
故选:C.
2.解:∵∠C=90°,
∴∠CAB+∠B=90°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE+∠B=90°,
∴∠CAB=∠BDE,
∵∠BDE=56°,
∴∠CAB=56°,
∵AD平分∠CAB,
∴∠DAE=∠CAB=28°,
故选:B.
3.解:∵∠B=54°,∠C=90°,
∴∠A=90°﹣54°=36°,
由折叠的性质可知,∠NEA=∠A=36°,
∴∠ENC=∠NEA+∠A=72°,
故选:C.
4.解:∵∠CAD=65°,AD平分∠CAE,
∴∠CAE=2∠CAD=130°,
∴∠BAC=180°﹣130°=50°,
∵∠B=30°,
∴∠ACD=∠B+∠BAC=30°+50°=80°.
故选:D.
5.解:∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
∵∠D+∠DAP=∠P+∠DCP①,
∠PAB+∠P=∠B+∠PCB②,
∴①﹣②得:∠D﹣∠P=∠P﹣∠B,
∴2∠P=∠D+∠B,
即∠P=(∠D+∠B).
故选:B.
6.解:在△FBC中,∠BFC=125°.
∴∠FBC+∠FCB=180°﹣∠BFC=55°.
∵BF平分∠ABC,CF平分∠ACB.
∴∠ABC=2∠FBC,∠ACB=2∠FCB.
∴∠ABC+∠ACB=2(∠FBC+∠FCB)=110°.
∴在△ABC中,∠A=180°﹣(∠ABC+∠ACB)=70°.
故选:C.
7.解:①∵BG⊥GD于点G,
∴∠G=90°.
∵GD∥BC,
∴∠G+∠GBC=180°.
∴∠GBC=180°﹣∠G=90°.
故①正确.
②∵GD∥BC,
∴∠GDB=∠DBC.
∵BE平分∠ABC,
∴∠ABC=2∠ABE.
∴∠GDB=2∠ABE.
故②正确.
③根据三角形外角的性质,得∠BFD=∠FBC+∠FCB,故③正确.
④由①知,∠GBC=∠GBF+∠FBC=90°.
∴∠EBG=90°﹣∠FBC.
∵∠AEB=∠ACB+∠EBC,
∴∠AEB=∠ABC﹣∠ABE+∠EBC.
∵∠A=90°,
∴∠ABC+∠ABC=180°﹣∠A=90°.
∴∠AEB=90°﹣∠ABE.
∵∵BE平分∠ABC,
∴∠ABE=∠EBC.
∴∠AEB=∠EBG.
故④正确.
⑤由④得,∠ABC+∠ACB=90°.
∵BE平分∠ABC,CD平分∠ACB,
∴∠EBC=,∠DCB=.
∴∠EBC+∠DCB=.
∴∠CFE=∠EBC+∠FCB=45°.
故⑤正确.
综上:正确的有①②③④⑤,共5个.
故选:A.
8.解:∵∠BA1是∠ABC的平分线,CA1是∠ACD和∠ACD的平分线,
∴∠ABA1=∠A1BC=∠ABC,∠ACA1=∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∴∠A1=∠A,
同理可得,∠A2=∠A1,∠A3=∠A2,
∴∠A3=∠A=×52°=6.5°,
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵∠A=114°,∠B=∠C,
∴114°+∠B+∠C=180°,
∴∠B=33°,
故答案为:33°.
10.解:∵△ABC中,∠A=65°,
∴∠B+∠C=180°﹣65°=115°,
∵∠B+∠C+∠1+∠2=360°,
∴∠1+∠2=360°﹣115°=245°,
故答案为:245.
11.解:∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°.
∵AD平分∠BAC,
∴∠DAC==40°.
∵EF∥AD,
∴∠G=∠DAC=40°.
故答案为:40°.
12.解:在△ABC中,∠B=80°,∠C=42°,
∴∠BAC=180°﹣∠B﹣∠C=58°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣42°=48°,
∴∠DAE=∠DAC﹣∠EAC=48°﹣29°=19°,
故答案为:19°.
13.解:∵∠B=50°,∠CEB=∠ADB﹣90°,
∴∠EHD=180°﹣50°=130°,
又∵∠EHD=∠AHC,
∴∠AHC=130°,
故答案为:130.
14.解:∵∠B=40°,∠C=30°,
∴∠BAC=110°,
∵∠BAE=50°,
∴∠CAE=60°,
∵△ADC沿直线AD折叠得到△ADE,
∴∠CAD=∠EAD=30°,
故答案为:30.
15.解:∵EF⊥AB,
∴∠AFE=90°,
∴∠A+∠AEF=90°,
∵∠A=40°,
∴∠AEF=50°,
∵∠AEF+∠DGE+∠GDE=180°,∠DGE=60°,
∴∠GDE=180°﹣50°﹣60°=70°,
∴∠ABD=∠GDE﹣∠A=70°﹣40°=30°,
∵BD是角平分线,
∴∠ABC=2∠ABD=60°,
∵BE是△ABC的高线,
∴BE⊥AC,
∴∠ABE+∠A=90°,
∴∠ABE=90°﹣40°=50°,
∴∠CBE=ABC﹣∠ABE=60°﹣50°=10°.
故答案为:10°.
16.解:①∵GH⊥BC,BG⊥AC,
∴∠BDC=∠BHG=90°,
∴∠G+∠GBH=∠DBC+∠C=90°,
∴∠G=∠C,
若∠ABD=∠C,则∠ABD=∠G,
则有AB∥GH,而已知条件并不能对此证明,
因此①错误.
②∵∠BEA=∠EBC+∠C,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠BEA=∠ABE+∠C,
由于①不能证明,故②也不能证明.
③显然,∠AFG=∠HFC (对顶角),
∵GH⊥BC,BG⊥AC,
∴∠FHC=∠BDC=90°,
∴∠HFC+∠C=90°,∠DBC+∠C=90°,
∴∠HFC=∠DBC=∠DBE+∠EBC,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠HFC=∠DBC=∠DBE+∠EBC=∠ABE+∠DBE,
因此,∠AFG=∠HFC=∠ABE+∠DBE,③正确.
④∵BG⊥AC,
∴∠ADB=∠BDC=90°,
∴∠A+∠ABD=∠DBC+∠C=90°,
∴∠A﹣∠C=∠DBC﹣∠ABD=∠DBE+∠EBC﹣∠ABD,
又∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠A﹣∠C=∠DBE+∠ABE﹣∠ABD=2∠DBE,
又∵∠BMH=∠DBE+∠G,
∴∠BMH=(∠A﹣∠C)+∠G,
即∠G+∠A=∠BMH+∠C,
故④正确,
故答案为:③④.
三.解答题(共6小题,满分40分)
17.解:∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC,
∵AD⊥BC,
∴∠ADE=90°,
即∠DAE+∠AED=90°,
而∠AED=∠C+∠CAE,
∴∠DAE+∠C+=90°,
∴2∠DAE+2∠C+∠BAC=180°,
即2∠DAE=180°﹣2∠C﹣∠BAC=∠B﹣∠C.
18.(1)证明:∵CD⊥AB于点D,EF⊥CD于点G,
∴AB∥EF,
∴∠B=∠EFC;
(2)解:∵∠A=60°,∠ACB=76°,
∴∠B=44°,
∵CD⊥AB,
∴∠BCD=90°﹣∠B=46°,
∵AB∥EF,
∴∠ADE=∠DEF,
∵∠ADE=∠EFC,
∴∠DEF=∠EFC,
∴DE∥BC,
∴∠CDE=∠BCD,
∴∠CDE=46°.
19.证明:(1)由题意可知,
∠BEF=∠1,∠BFE=∠ADB,
∴∠BEF+∠BFE=∠1+ADB,
∴180°﹣(∠BEF+∠BFE)=180°﹣(∠1+ADB),
即∠B=∠GDC,
∴AB∥DG.
解:(2)∵DG是∠ADC的平分线,且AB∥DG,
∴∠1=∠DGC=∠B,
∵∠2=3∠B+40°,
∴180°﹣∠1=3∠B+40°,
∴180°﹣∠B=3∠B+40°,
∴∠B=35°.
20.解:(1)∵BP、CP为∠ABC和∠ACB的角平分线,
∴∠CBP=,∠BCP=.
∴∠CBP+∠CBP=.
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A.
∴∠PBC+∠PCB=.
∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣=90°+.
(2)∵∠P+∠PBC=∠PCD,
∴∠P=∠PCD﹣∠PBC.
∵BP、CP为∠ABC和∠ACE的角平分线,
∴∠PCD=,∠PBC=.
∴∠P==.
(3)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=∠A+∠ACB+∠A+∠ABC=180°+∠A.
∵BP、CP为∠CBD和∠BCE的角平分线,
∴∠CBP=,∠BCP=.
∴=.
∴∠P=180°﹣(∠CBP+∠BCP)=180°﹣=90°﹣.
21.(1)证明:∵∠C+∠CBE+∠CEB=180°,∠AED+∠1+∠CEB=180°,∠C=∠1,
∴∠CBE=∠AED;
(2)解:∵∠D+∠ABC=180°,∠D=124°,
∴∠ABC=56°,
∵BE平分∠ABC,
∴∠CBE=∠ABC=28°,
∵∠C+∠CBE+∠CEB=180°,∠C=80°,
∴∠CEB=72°.
22.解:(1)①∵BM∥DG,
∴∠ABM=∠F=30°,
∵BM为△ABC的角平分线,
∴∠ABC=2∠ABM=60°,
故答案为:60°;
②证明:由①得,∠CBM=∠ABM=30°,
∵BM∥DG,
∴∠DGC=∠CBM=30°,
∵DE⊥BC,
∴∠EDG=60°,
∵DG平分∠ADE,
∴∠ADF=60°,
∴∠A=180°﹣30°﹣60°=90°,
∴AC⊥AB;
(2)45°﹣.
理由:由八字模型可得,△BHG和△DEG中,
∠BHD=∠EDG+90°﹣∠HBG=∠ADE+90°﹣(180°﹣ABC)=(∠ADE+∠ABC)﹣90°=45°﹣.
故答案为:45°﹣;
(3)①如图,
由八字模型可得,△ABM和△NMD中,
∠BND=∠ABN+∠A﹣∠MDN=∠ABC+α﹣(90°﹣∠ACB)=(∠ABC+∠ACB)+α﹣45°=45°+;
②如图,
由四边形的内角和得,
∠BND=360°﹣90°﹣ABC﹣ADE=270°﹣(270°﹣α)=135°+;
③如图,
由八字模型可得,∠BND+∠ABM=∠ADG+∠DAB,
∴∠BND=∠ADE+(180°﹣α)﹣ABC=(90°﹣∠ACB)+(180°﹣α)﹣ABC=135°﹣;
综上,∠BND=45°+或135°±.
