2022-2023学年北师大版九年级数学上册 三角形相似的判定同步练习 (word版 含答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学上册 三角形相似的判定同步练习 (word版 含答案) | 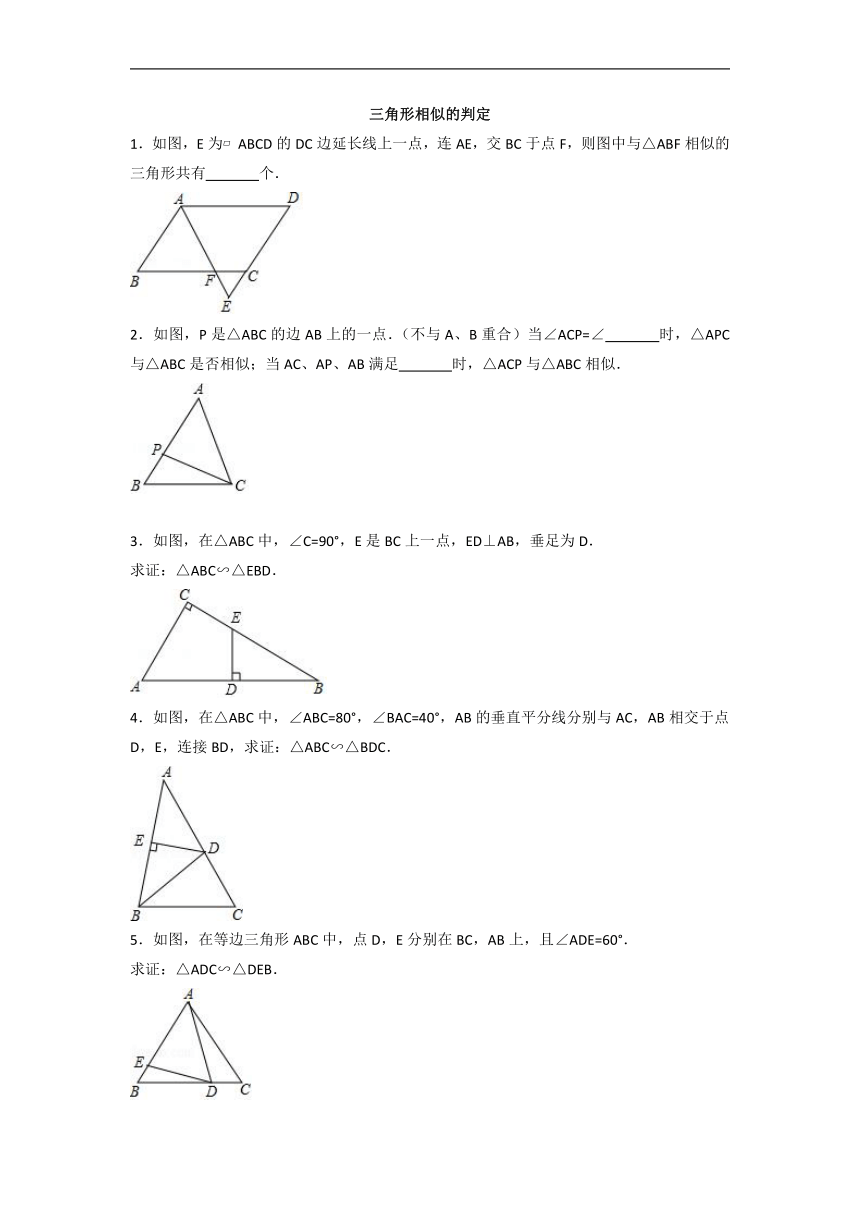 | |
| 格式 | docx | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 10:59:00 | ||
图片预览



文档简介
三角形相似的判定
1.如图,E为 ABCD的DC边延长线上一点,连AE,交BC于点F,则图中与△ABF相似的三角形共有 个.
2.如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ 时,△APC与△ABC是否相似;当AC、AP、AB满足 时,△ACP与△ABC相似.
3.如图,在△ABC中,∠C=90°,E是BC上一点,ED⊥AB,垂足为D.
求证:△ABC∽△EBD.
4.如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB相交于点D,E,连接BD,求证:△ABC∽△BDC.
5.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.
求证:△ADC∽△DEB.
6.已知:如图,在△ABC中,点D在BC上,点E在AC上,DE与AB不平行.添加一个条件 ,使得△CDE∽△CAB,然后再加以证明.
7.如图,在△ABC和△ADE中,AB/AD=BC/DE=AC/AE,点B.D.E在一条直线上,求证:△ABD∽△ACE.
8.如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,求证:△FED∽△DEB.
9.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
10.如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
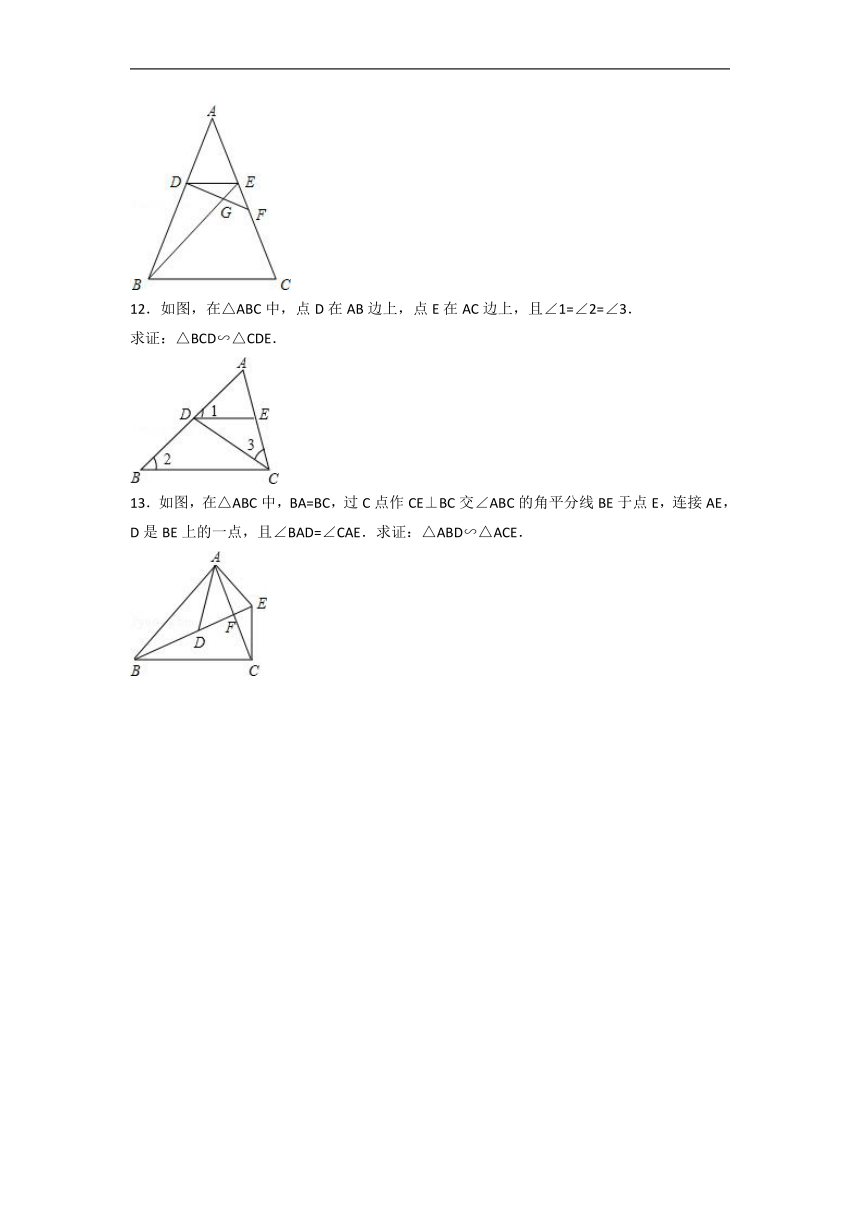
11.如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:△DEF∽△BDE.
12.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3.
求证:△BCD∽△CDE.
13.如图,在△ABC中,BA=BC,过C点作CE⊥BC交∠ABC的角平分线BE于点E,连接AE,D是BE上的一点,且∠BAD=∠CAE.求证:△ABD∽△ACE.
参考答案与试题解析
1.如图,E为 ABCD的DC边延长线上一点,连AE,交BC于点F,则图中与△ABF相似的三角形共有 2 个.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△CEF,△CEF∽△AED,
∴△ABF∽△AED.
∴图中与△ABF相似的三角形是:△CEF,△AED.
故答案为:2
2.如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ B 时,△APC与△ABC是否相似;当AC、AP、AB满足 时,△ACP与△ABC相似.
【解答】解:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC;
∵,∠A=∠A,
∴△ACP与△ABC;
故答案为:B;.
3.如图,在△ABC中,∠C=90°,E是BC上一点,ED⊥AB,垂足为D.
求证:△ABC∽△EBD.
【解答】证明:∵ED⊥AB,
∴∠EDB=90°,
∵∠C=90°,
∴∠EDB=∠C,
∵∠B=∠B,
∴△ABC∽△EBD.
4.如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB相交于点D,E,连接BD,求证:△ABC∽△BDC.
【解答】证明:
∵DE是AB的垂直平分线,
∴AD=BD.
∵∠BAC=40°,
∴∠ABD=40°,
∵∠ABC=80°,
∴∠DBC=40°,
∴∠DBC=∠BAC,
∵∠C=∠C,
∴△ABC∽△BDC.
5.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.
求证:△ADC∽△DEB.
【解答】证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠ADB=∠CAD+∠C=∠CAD+60°,
∵∠ADE=60°,
∴∠ADB=∠BDE+60°,
∴∠CAD=∠BDE,
∴△ADC∽△DEB.
6.已知:如图,在△ABC中,点D在BC上,点E在AC上,DE与AB不平行.添加一个条件 ∠CDE=∠A ,使得△CDE∽△CAB,然后再加以证明.
【解答】解:添加条件为:∠CDE=∠A,
理由:∵∠C=∠C,
∠CDE=∠A,
∴△CDE∽△CAB.
故答案为:∠CDE=∠A.
7.如图,在△ABC和△ADE中,AB/AD=BC/DE=AC/AE,点B.D.E在一条直线上,求证:△ABD∽△ACE.
【解答】证明:∵在△ABC和△ADE中,,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵,
∴,
∴△ABD∽△ACE.
8.如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,求证:△FED∽△DEB.
【解答】证明:∵四边形ABCD是矩形,
∴∠BAE=90°,∵∠AFE=∠BFA=90°,
∴∠AFE=∠BAE,∵∠AEF=∠BEA,
∴△AFE∽△BAE,
得 =,
又∵AE=ED,
∴=,而∠BED=∠BED,
∴△FED∽△DEB.
9.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
【解答】证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
10.如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
【解答】证明:∵CE=CD,
∴∠CED=∠CDE,
∴∠AEC=∠ADB,
∵∠DAC=∠B,
∴△ACE∽△BAD.
11.如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:△DEF∽△BDE.
【解答】证明:∵AB=AC,
∴∠ABC=∠ACB.
∵DE∥BC,
∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.
∴∠BDE=∠CED.
∵∠EDF=∠ABE,
∴△DEF∽△BDE.
12.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3.
求证:△BCD∽△CDE.
【解答】证明:∵∠DEC=∠1+∠A,∠BDC=∠3+∠A,
∵∠1=∠3,
∴∠BDC=∠DEC,
∵∠2=∠3,
∴△BCD∽△CDE.
13.如图,在△ABC中,BA=BC,过C点作CE⊥BC交∠ABC的角平分线BE于点E,连接AE,D是BE上的一点,且∠BAD=∠CAE.求证:△ABD∽△ACE.
【解答】解:∵BA=BC,BE平分∠ABC,
∴∠ABE=∠CBE,BE⊥AC(等腰三角形三线合一的性质),
∴∠CBE+∠ACB=90°,
又∵CE⊥BC,
∴∠ACE+∠ACB=90°,
∴∠CBE=∠ACE,
∴∠ABE=∠ACE,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
1.如图,E为 ABCD的DC边延长线上一点,连AE,交BC于点F,则图中与△ABF相似的三角形共有 个.
2.如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ 时,△APC与△ABC是否相似;当AC、AP、AB满足 时,△ACP与△ABC相似.
3.如图,在△ABC中,∠C=90°,E是BC上一点,ED⊥AB,垂足为D.
求证:△ABC∽△EBD.
4.如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB相交于点D,E,连接BD,求证:△ABC∽△BDC.
5.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.
求证:△ADC∽△DEB.
6.已知:如图,在△ABC中,点D在BC上,点E在AC上,DE与AB不平行.添加一个条件 ,使得△CDE∽△CAB,然后再加以证明.
7.如图,在△ABC和△ADE中,AB/AD=BC/DE=AC/AE,点B.D.E在一条直线上,求证:△ABD∽△ACE.
8.如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,求证:△FED∽△DEB.
9.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
10.如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
11.如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:△DEF∽△BDE.
12.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3.
求证:△BCD∽△CDE.
13.如图,在△ABC中,BA=BC,过C点作CE⊥BC交∠ABC的角平分线BE于点E,连接AE,D是BE上的一点,且∠BAD=∠CAE.求证:△ABD∽△ACE.
参考答案与试题解析
1.如图,E为 ABCD的DC边延长线上一点,连AE,交BC于点F,则图中与△ABF相似的三角形共有 2 个.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△CEF,△CEF∽△AED,
∴△ABF∽△AED.
∴图中与△ABF相似的三角形是:△CEF,△AED.
故答案为:2
2.如图,P是△ABC的边AB上的一点.(不与A、B重合)当∠ACP=∠ B 时,△APC与△ABC是否相似;当AC、AP、AB满足 时,△ACP与△ABC相似.
【解答】解:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC;
∵,∠A=∠A,
∴△ACP与△ABC;
故答案为:B;.
3.如图,在△ABC中,∠C=90°,E是BC上一点,ED⊥AB,垂足为D.
求证:△ABC∽△EBD.
【解答】证明:∵ED⊥AB,
∴∠EDB=90°,
∵∠C=90°,
∴∠EDB=∠C,
∵∠B=∠B,
∴△ABC∽△EBD.
4.如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC,AB相交于点D,E,连接BD,求证:△ABC∽△BDC.
【解答】证明:
∵DE是AB的垂直平分线,
∴AD=BD.
∵∠BAC=40°,
∴∠ABD=40°,
∵∠ABC=80°,
∴∠DBC=40°,
∴∠DBC=∠BAC,
∵∠C=∠C,
∴△ABC∽△BDC.
5.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.
求证:△ADC∽△DEB.
【解答】证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠ADB=∠CAD+∠C=∠CAD+60°,
∵∠ADE=60°,
∴∠ADB=∠BDE+60°,
∴∠CAD=∠BDE,
∴△ADC∽△DEB.
6.已知:如图,在△ABC中,点D在BC上,点E在AC上,DE与AB不平行.添加一个条件 ∠CDE=∠A ,使得△CDE∽△CAB,然后再加以证明.
【解答】解:添加条件为:∠CDE=∠A,
理由:∵∠C=∠C,
∠CDE=∠A,
∴△CDE∽△CAB.
故答案为:∠CDE=∠A.
7.如图,在△ABC和△ADE中,AB/AD=BC/DE=AC/AE,点B.D.E在一条直线上,求证:△ABD∽△ACE.
【解答】证明:∵在△ABC和△ADE中,,
∴△ABC∽△ADE,
∴∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵,
∴,
∴△ABD∽△ACE.
8.如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,求证:△FED∽△DEB.
【解答】证明:∵四边形ABCD是矩形,
∴∠BAE=90°,∵∠AFE=∠BFA=90°,
∴∠AFE=∠BAE,∵∠AEF=∠BEA,
∴△AFE∽△BAE,
得 =,
又∵AE=ED,
∴=,而∠BED=∠BED,
∴△FED∽△DEB.
9.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
【解答】证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
10.如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
【解答】证明:∵CE=CD,
∴∠CED=∠CDE,
∴∠AEC=∠ADB,
∵∠DAC=∠B,
∴△ACE∽△BAD.
11.如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:△DEF∽△BDE.
【解答】证明:∵AB=AC,
∴∠ABC=∠ACB.
∵DE∥BC,
∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.
∴∠BDE=∠CED.
∵∠EDF=∠ABE,
∴△DEF∽△BDE.
12.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3.
求证:△BCD∽△CDE.
【解答】证明:∵∠DEC=∠1+∠A,∠BDC=∠3+∠A,
∵∠1=∠3,
∴∠BDC=∠DEC,
∵∠2=∠3,
∴△BCD∽△CDE.
13.如图,在△ABC中,BA=BC,过C点作CE⊥BC交∠ABC的角平分线BE于点E,连接AE,D是BE上的一点,且∠BAD=∠CAE.求证:△ABD∽△ACE.
【解答】解:∵BA=BC,BE平分∠ABC,
∴∠ABE=∠CBE,BE⊥AC(等腰三角形三线合一的性质),
∴∠CBE+∠ACB=90°,
又∵CE⊥BC,
∴∠ACE+∠ACB=90°,
∴∠CBE=∠ACE,
∴∠ABE=∠ACE,
∵∠BAD=∠CAE,
∴△ABD∽△ACE.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
