第十二章全等三角形导学案
文档属性
| 名称 | 第十二章全等三角形导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-23 21:38:57 | ||
图片预览




文档简介
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.1 全等三角形 课型 新授
第1课时 主备教师 上课教师 审核人
学习目标 1、了解全等形及全等三角形的概念。理解掌握全等三角形的性质。2、能够准确辩认全等三角形的对应元素。3、在探究和运用全等三角形性质的过程中感受到数学活动的乐趣。
教学重点 难点 【重点】全等三角形的概念及性质.【难点】找全等三角形的对应边、对应角.
教 学 过 程 修改内容
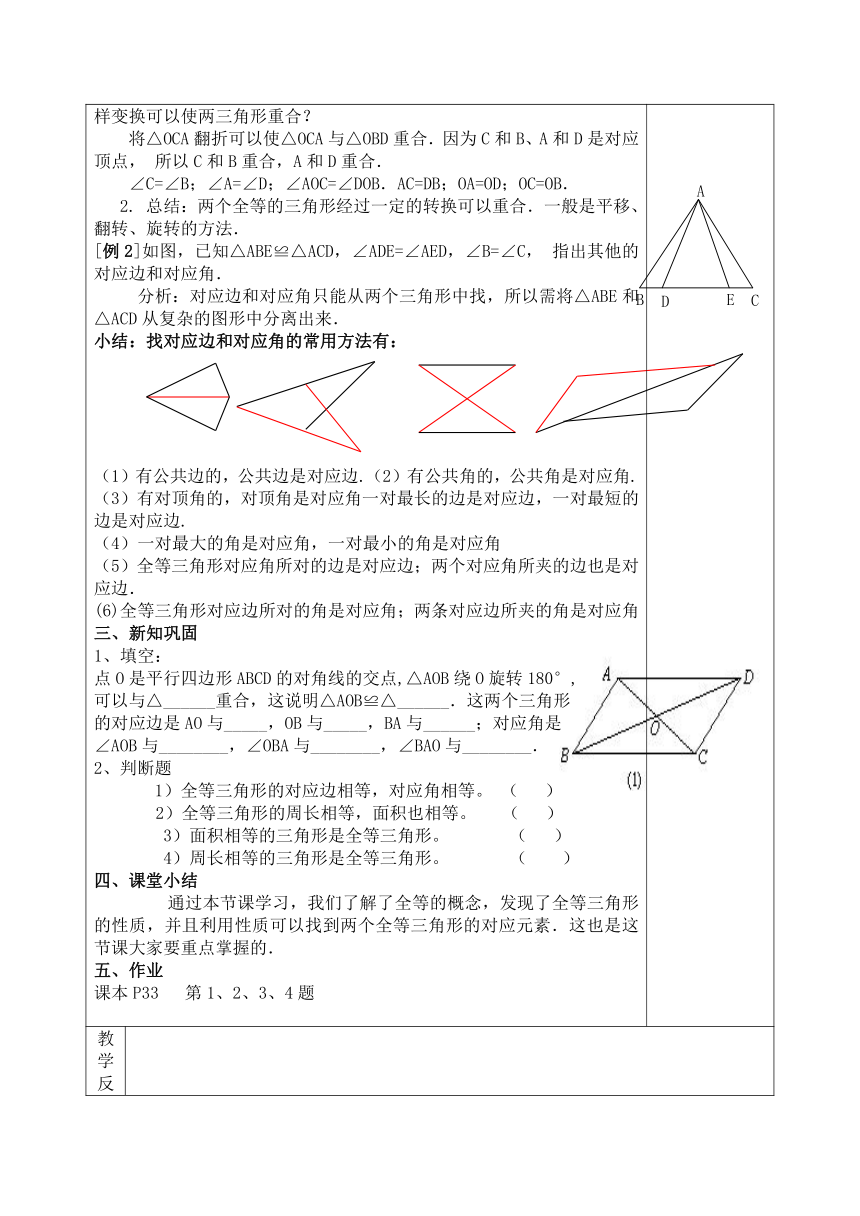
情景引入:出示投影片:1.问题:你能发现这两个图形有什么美妙的关系吗?2.那同学们能举出现实生活中能够完全重合的图形的例子吗 3.动手操作:取一张纸,将自己事先准备好的三角板按在纸上,画下图形,照图形裁下来,纸样与三角板形状、大小完全一样.4.获取概念:让学生用自己的语言叙述:全等形、全等三角形、对应顶点、对应角、对应边,以及有关的数学符号.记作:△ABC ≌ △ A’B’C’ 符号“ ≌ ”读作“全等于”(注意强调书写时对应顶点字母写在对应的位置上)二、新知探究 利用投影片演示1.活动:将△ABC沿直线BC平移得△DEF;将△ABC沿BC翻折180 得到△DBC; 将△ABC旋转180°得△AED. 2. 议一议:各图中的两个三角形全等吗? 启示:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略. 3. 观察与思考: 寻找甲图中两三角形的对应元素,它们的对应边有什么关系?对应角呢? (引导学生从全等三角形可以完全重合出发找等量关系)得到全等三角形的性质:全等三角形的对应边相等.全等三角形的对应角相等.[例1]如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角. 1. 分析:△OCA≌△OBD,说明这两个三角形可以重合,思考通过怎样变换可以使两三角形重合?将△OCA翻折可以使△OCA与△OBD重合.因为C和B、A和D是对应顶点,所以C和B重合,A和D重合. ∠C=∠B;∠A=∠D;∠AOC=∠DOB.AC=DB;OA=OD;OC=OB. 2. 总结:两个全等的三角形经过一定的转换可以重合.一般是平移、翻转、旋转的方法.[例2]如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.分析:对应边和对应角只能从两个三角形中找,所以需将△ABE和△ACD从复杂的图形中分离出来.小结:找对应边和对应角的常用方法有:(1)有公共边的,公共边是对应边.(2)有公共角的,公共角是对应角. (3)有对顶角的,对顶角是对应角一对最长的边是对应边,一对最短的边是对应边.(4)一对最大的角是对应角,一对最小的角是对应角(5)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.(6)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角三、新知巩固1、填空:点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180°,可以与△______重合,这说明△AOB≌△______.这两个三角形的对应边是AO与_____,OB与_____,BA与______;对应角是∠AOB与________,∠OBA与________,∠BAO与________.2、判断题1)全等三角形的对应边相等,对应角相等。 ( ) 2)全等三角形的周长相等,面积也相等。 ( ) 3)面积相等的三角形是全等三角形。 ( ) 4)周长相等的三角形是全等三角形。 ( )四、课堂小结通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素.这也是这节课大家要重点掌握的.五、作业课本P33 第1、2、3、4题
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 八 教学课题 12.2 三角形全等的判定(1) 课型
第2课时 主备教师 上课教师 审核人
学习目标 1、经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.2、掌握三角形全等的“边边边”条件,3、通过对问题的共同探讨,培养学生的协作精神.
教学重点 难点 【重点】三角形全等的“边边边”判定方法。【难点】运用“边边边”进行简单的证明。
教 学 过 程 修改内容
一、预习导学:预习教材P35-37页,并尝试完成自主预习案。二、新知探究 合作交流:多媒体显示:复习全等三角形的定义及其性质,结论:全等三角形三条边对应相等,三个角分别对应相等.反之,这六个元素分别相等,这样的两个三角形一定全等.两个三角形全等,是否一定需要六个条件呢 如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢 组织学生进行讨论交流,经过学生逐步分析,各种情况逐渐明朗,进行交流予以汇总归纳.探究一:先任意画一个△ABC,再画一个△A'B'C',使△ABC与△A'B'C',满足上述条件中的一个或两个.你画出的△A'B'C'与△ABC一定全等吗 让学生按照下面给出的条件作出三角形. (1)三角形的两个角分别是30°、50°. (2)三角形的两条边分别是4cm,6cm. (3)三角形的一个角为30°,—条边为3cm.再通过画一画,剪一剪,比一比的方式,得出结论:只给出一个或两个条件时,都不能保证所画出的三角形一定全等. 探究二:先任意画出一个△A'B'C',使A'B'=AB,B'C'=BC,C'A'=CA,把画好的△A'B'C'剪下,放到△ABC上,它们全等吗 让学生充分交流后,在教师的引导下作出△A'B'C',并通过比较得出结论:三边对应相等的两个三角形全等.【例l】如下图△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证△ABD≌△ACD.让学生独立思考后口头表达理由,再让学生展示。师生共同检查学生展示内容,要特别强调证明格式的书写。【例2】如图,已知∠AOB,求作:∠A/O/B/,使∠A/O/B/=∠AOB。【教师点评】师生共同分析,探讨作图过程,让学生理解并掌握每一步的具体作法。 思考:为什么这样作出的∠A/O/B/和∠AOB是相等的。 让学生自己任意画一个角,巩固作图方法。三、新知巩固1、如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试.2、教材P37第1、2题。四、课堂小结:回顾反思本节课对知识的研究探索过程、小结方法及结论,提炼数学思想,掌握数学规律.例3 如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试.五、作业1、课本P43练习第1题.2、.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 教学课题 12.2 三角形全等的判定(2) 课型
第3课时 主备教师 上课教师 审核人
学习目标 1、探索三角形全等条件之二:SAS,培养学生观察分析图形能力、动手能力.2、在探索三角形全等条件及其运用的过程中,体验操作、归纳得出数学结论的方法。
教学重点 难点 【重点】应用“边角边”证明两个三角形全等,进而得出线段或角相等.【难点】教学难点指导学生分析问题,寻找判定三角形全等的条件.
教 学 过 程 修改内容
一、预习导学:预习教材P37-39页,并尝试回答下列问题:多媒体出示探究3:已知任意△ABC,画△A'B'C',使A'B'=AB,A'C'=AC,∠A'=∠A.【教帅点拨】学生边学边画图,再让学生把画好的△A'B'C',剪下放在△ABC上,观察回答:1、通过对“探究三”的阅读理解,你得到了什么?2、通过对“例2”的阅读理解,你又得到了什么?3、继续阅读“探究四”,你有什么发现?根据前面的操作学习,鼓励学生用自己的语言来总结规律: 【两边和它们的夹角对应相等的两个三角形全等.(SAS)】 补充强调:角必须是两条相等的对应边的夹角,边必须是夹相等角的两对边.二、新知探究 合作交流出示例2,如图,有—池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么 让学生充分思考后,书写推理过程,并说明每一步的依据. (教师也可作如下分析: 要想证AB=DE, 只需证△ABC≌△DECABC与△DEC全等的条件现有_________还需要________________________)补充例题:1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE 求证: △ABD≌△ACE证明:∵∠BAC=∠DAE(已知) ∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD ∴∠BAD=∠CAE 在△ABD与△ACE中 AB=AC(已知) ∠BAD= ∠CAE (已证) AD=AE(已知) ∴△ABD≌△ACE(SAS)变式一:求证:1.BD=CE 2. ∠B= ∠C 3. ∠ADB= ∠AEC【明确:证明分别属于两个三角形的线段相等或者角相等的问题,常常通过证明这两个三角形全等来解决.】三、再次探究,释解疑惑探究4,我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗 为什么 让学生模仿前面的探究方法,得出结论:两边及其中一边的对角对应相等的两个三角形不一定全等. 四、巩固练习1、课本P39页,1、2.2、补充:已知:如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE.
求证: △DAC≌△EABBE=DC ∠B= ∠ C ∠ D= ∠ E BE⊥CD五、课堂小结1.判定三角形全等的方法;2.证明线段、角相等常见的方法有哪些 让学生自由表述,其他学生补充,六、作业1.课本P43页,第2、3、4题.2.选作题:(1)小明做了一个如图所示的风筝,测得DE=DF,EH=FH,你能发现哪些结沦 并说明理由.(2)如图,∠1=∠2,AB=AD,AE=AC,求证BC=DE.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.2.3 三角形全等的条件(3) 课型 新授
第4课时 主备教师 上课教师 审核人
学习目标 1、掌握三角形全等的“角边角”“角角边”条件 2.能运用全等三角形的条件,解决简单的推理证明问题在探究中感受推理的魅力,在成功中获得喜悦,在分析中提升思维能力。
教学重点 难点 【重点】已知两角一边的三角形全等探究.【难点】灵活运用三角形全等条件证明
教 学 过 程 修改内容
一、提出问题,创设情境1.复习:(1)三角形中已知三个元素,包括哪几种情况? 三个角、三个边、两边一角、两角一边.(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?三种:①定义;②SSS;③SAS. 2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?二、新课讲解问题1:三角形中已知两角一边有几种可能? 1.两角和它们的夹边. 2.两角和其中一角的对边.问题2:三角形的两个内角分别是60°和80°,它们的夹边为4cm,你能画一个三角形同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是不是全等,你能得出什么规律? 将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.提炼规律:两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).问题3:我们刚才做的三角形是一个特殊三角形,画任意一个三角形ABC,能不能作一个△A′B′C′,使∠A=∠A′、∠B=∠B′、AB=A′B′呢?作法 ① 作线段A′B′,使A′B′=AB ② 分别以A′、B′为顶点,A′B′为一边在同一侧作∠DA′B′、∠EB′A,使∠D′AB=∠CAB,∠EB′A′=∠CBA. ③射线A′D与B′E交于一点,记为C′ 即可得到△A′B′C′. 将△A′B′C′与△ABC重 叠,发现两三角形全等.两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”). 思考:在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢? 问题4:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗? 证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180° ∠A=∠D,∠B=∠E ∴∠A+∠B=∠D+∠E ∴∠C=∠F 在△ABC和△DEF中 ∴△ABC≌△DEF(ASA). 两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).5.探究:对于三个角对应相等的两个三角形全等吗?如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。三个角对应相等的两个三角形不一定全等 [例]如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE. [分析]AD和AE分别在△ADC和△AEB中,所以要证AD=AE,只需证明△ADC≌△AEB即可.三、新知巩固 1.课本P13练习1、2.2.补充练习图中的两个三角形全等吗?请说明理由.四、课堂小结 我们有五种判定三角形全等的方法:【边边边(SSS) 边角边(SAS) 角边角(ASA) 角角边(AAS)】 推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径.五、作业 1.教材P44页 第4、7、8题.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.2 三角形全等的条件(4) 课型 新授
第5课时 主备教师 上课教师 审核人
学习目标 1、掌握直角三角形全等的条件,并能运用其解决一些实际问题2、经历探索Rt△全等条件的过程,体会利用操作、归纳获得数学结论的过程;
教学重点 难点 【重点】运用直角三角形全等的条件解决一些实际问题。【难点】熟练运用直角三角形全等的条件解决一些实际问题。
教 学 过 程 修改内容
一、预习导学:1、判定两个三角形全等的方法: 、 、 、 2、如图,Rt△ABC中,直角边是 、 , 斜边是 3、如图,AB⊥BE于C,DE⊥BE于E,(1)若∠A=∠D,AB=DE,则△ABC与△DEF _______根据 (用简写法)(2)若∠A=∠D,BC=EF,则△ABC与△DEF 根据 (用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF 根据 (用简写法)(4)若AB=DE,BC=EF,AC=DF则△ABC与△DEF 根据 (用简写法)二、新知探究探索练习:(动手操作): 已知线段a ,c (a教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.3 角的平分线的性质(1) 课型 新授
第6课时 主备教师 上课教师 审核人
学习目标 1、应用三角形全等的知识,解释角平分线的原理.2、会用尺规作一个已知角的平分线.3、角平分线的性质。
教学重点 难点 【重点】利用尺规作已知角的平分线.【难点】角的平分线的作图方法的提炼.
教 学 过 程 修改内容
一、预习导学: 生预习教材P48-49页,完成自主预习案。二、新知探究: 1. 议一议: 下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?即射线AC就是∠DAB的平分线.根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)2.作已知角的平分线的方法:已知: ∠AOB(如图)求作: ∠AOB的角平分线OC.作法:1、以O为圆心,适当长为半径作弧,交OA于M,交OB于N。2、分别以M、N为圆心,大于MN的长为半径作弧,两弧在∠AOB内部交于点C。3、作射线OC,射线OC即为所求。练一练:任意画一角∠AOB,作它的平分线.2、探究:下面用我们学过的知识证明发现:如图,已知AO平分∠BAC,OE⊥AB,OD⊥AC求证:OE=OD。让学生自己独立完成证明过程角平分线的性质定理:角平分线上的点到角的两边的距离相等数学语言:∵AO平分∠BOC,OE⊥AB,OD⊥OC ∴ OE=OD 如何更直观的表达题意?我们通常在证明之前画出图形,并用符号表示出已知与求证【补充例题】已知:如图,△ABC中 ∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,求证:CF=EB分析:要证CF=EB,首先我们想到的是要证它们所在的两个三角形全等,即Rt△CDF ≌ Rt△EDB. 现已有一个条件BD=DF(斜边相等),还需要我们找什么条件DC=DE (因为角的平分线的性质) 再用HL证明. 学生尝试完成证明过程。三、新知巩固课本P50第1题。 练后总结:平角∠AOB的平分线OC与直线AB垂直. 将OC反向延长得到直线CD,直线CD与AB也垂直.四、课时小结 本节课中我们利用已学过的三角形全等的知识,探究得到了角平分线仪器的操作原理, 由此归纳出角的平分线的尺规画法,并进一步探究到角平分线的性质.五、作业:1、教材P51第1、2题六、课后思考:思考:在一节数学课上,老师要求同学们练习一道题,题目的图形如图所示,图中的BD是∠ABC的平分线,在同学们忙于画图和分析题目时,小明同学忽然兴奋地大声说:“我有个发现!”原来他自己创造了一个在直角三角形中画锐角的平分线的方法.他的方法是这样的,在AB上取点E,使BE=BC,然后画DE⊥AB交AC于D,那么BD就是∠ABC的平分线.有的同学对小明的画法表示怀疑,你认为他的画法对不对呢?请你来说明理由.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.3角的平分线的性质(2) 课型 新授
第7课时 主备教师 上课教师 审核人
学习目标 1、会叙述角的平分线的性质的逆定理“到角两边距离相等的点在角的平分线上”.2、能应用这个定理解决一些简单的实际问题.3、在操作中让学生经历了思考,仔细,合作,提升学生认真的习惯。
教学重点 难点 【重点】角平分线性质的逆定理及其应用.【难点】灵活应用两个性质解决问题.
教 学 过 程 修改内容
一、预习导学: 1、角的平分线性质定理的内容是什么?其中题设、结论是什么?2、角平分线性质定理的作用是证明什么?3、填空 如图:∵OC平分∠AOB, ∴AC=BC(角平分线性质定理)思考:怎样判定一个点是否在已知角的平分线上?二、新知探究:1、逆向思维探求角平分线的判定定理问: 把角平分线性质定理的题设、结论交换后,得出什么命题? 它正确?如何证明?指出:以上问题是我们今天所要解决的重点。2、证明上面提问得出的猜想:如果一个点到角的两边的距离相等,那么这个点在角的平分线上。已知:PD⊥OA于D,PE⊥OB于E,PD=PE求证:点P在∠AOB的平分线上分析: 直角△DOP≌直角△EOP证明:(学生板书)3、引导学生得出角平分线判定定理: 到一个角的两边的距离相等的点,在这个角的平分线上。【例题】现有一题目,两位同学分别用两种方法证明,问他们的做法正确?那一种方法好?已知:, CA⊥OA于A,BC⊥OB于B,AC=BC求证: OC平分∠AOB证法1:∵CA⊥OA,BC⊥OB∴∠A=∠B在△AOC和△BOC中∴△AOC≌△BOC(HL)∴∠AOC=∠BOC ∴OC平分∠AOB证法2:∵ CA⊥OA于A,BC⊥OB于B, AC=BC∴OC平分∠AOB(角平分线判定定理)指出:在已知一定条件下,证角平分线不再用三角形全等后角相等得出,可直接运用角平分线判定定理。三、新知巩固 1 、P 50 第2题 2 、完成当堂评价案四、小结 1、 角平分线的判定定理是什么?它的作用是用来证 明什么相等? 2、在已知一定条件下,证角平分线不再用三角形全等后角相等得出,可直接运用角平分线判定定理。五、作业 1如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠BAO=∠CAO2.已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD 求证:⑴△BDE≌△CDF ⑵点D在∠A的平分线上
教学反思
A
B
C
D
E
A
C
D
E
B
F
B
A
D
C
E
F
_年 月 日
学科 数学 年级 七 教学课题 12.1 全等三角形 课型 新授
第1课时 主备教师 上课教师 审核人
学习目标 1、了解全等形及全等三角形的概念。理解掌握全等三角形的性质。2、能够准确辩认全等三角形的对应元素。3、在探究和运用全等三角形性质的过程中感受到数学活动的乐趣。
教学重点 难点 【重点】全等三角形的概念及性质.【难点】找全等三角形的对应边、对应角.
教 学 过 程 修改内容
情景引入:出示投影片:1.问题:你能发现这两个图形有什么美妙的关系吗?2.那同学们能举出现实生活中能够完全重合的图形的例子吗 3.动手操作:取一张纸,将自己事先准备好的三角板按在纸上,画下图形,照图形裁下来,纸样与三角板形状、大小完全一样.4.获取概念:让学生用自己的语言叙述:全等形、全等三角形、对应顶点、对应角、对应边,以及有关的数学符号.记作:△ABC ≌ △ A’B’C’ 符号“ ≌ ”读作“全等于”(注意强调书写时对应顶点字母写在对应的位置上)二、新知探究 利用投影片演示1.活动:将△ABC沿直线BC平移得△DEF;将△ABC沿BC翻折180 得到△DBC; 将△ABC旋转180°得△AED. 2. 议一议:各图中的两个三角形全等吗? 启示:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略. 3. 观察与思考: 寻找甲图中两三角形的对应元素,它们的对应边有什么关系?对应角呢? (引导学生从全等三角形可以完全重合出发找等量关系)得到全等三角形的性质:全等三角形的对应边相等.全等三角形的对应角相等.[例1]如图,△OCA≌△OBD,C和B,A和D是对应顶点,说出这两个三角形中相等的边和角. 1. 分析:△OCA≌△OBD,说明这两个三角形可以重合,思考通过怎样变换可以使两三角形重合?将△OCA翻折可以使△OCA与△OBD重合.因为C和B、A和D是对应顶点,所以C和B重合,A和D重合. ∠C=∠B;∠A=∠D;∠AOC=∠DOB.AC=DB;OA=OD;OC=OB. 2. 总结:两个全等的三角形经过一定的转换可以重合.一般是平移、翻转、旋转的方法.[例2]如图,已知△ABE≌△ACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.分析:对应边和对应角只能从两个三角形中找,所以需将△ABE和△ACD从复杂的图形中分离出来.小结:找对应边和对应角的常用方法有:(1)有公共边的,公共边是对应边.(2)有公共角的,公共角是对应角. (3)有对顶角的,对顶角是对应角一对最长的边是对应边,一对最短的边是对应边.(4)一对最大的角是对应角,一对最小的角是对应角(5)全等三角形对应角所对的边是对应边;两个对应角所夹的边也是对应边.(6)全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角三、新知巩固1、填空:点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180°,可以与△______重合,这说明△AOB≌△______.这两个三角形的对应边是AO与_____,OB与_____,BA与______;对应角是∠AOB与________,∠OBA与________,∠BAO与________.2、判断题1)全等三角形的对应边相等,对应角相等。 ( ) 2)全等三角形的周长相等,面积也相等。 ( ) 3)面积相等的三角形是全等三角形。 ( ) 4)周长相等的三角形是全等三角形。 ( )四、课堂小结通过本节课学习,我们了解了全等的概念,发现了全等三角形的性质,并且利用性质可以找到两个全等三角形的对应元素.这也是这节课大家要重点掌握的.五、作业课本P33 第1、2、3、4题
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 八 教学课题 12.2 三角形全等的判定(1) 课型
第2课时 主备教师 上课教师 审核人
学习目标 1、经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程.2、掌握三角形全等的“边边边”条件,3、通过对问题的共同探讨,培养学生的协作精神.
教学重点 难点 【重点】三角形全等的“边边边”判定方法。【难点】运用“边边边”进行简单的证明。
教 学 过 程 修改内容
一、预习导学:预习教材P35-37页,并尝试完成自主预习案。二、新知探究 合作交流:多媒体显示:复习全等三角形的定义及其性质,结论:全等三角形三条边对应相等,三个角分别对应相等.反之,这六个元素分别相等,这样的两个三角形一定全等.两个三角形全等,是否一定需要六个条件呢 如果只满足上述六个条件中的一部分,是否也能保证两个三角形全等呢 组织学生进行讨论交流,经过学生逐步分析,各种情况逐渐明朗,进行交流予以汇总归纳.探究一:先任意画一个△ABC,再画一个△A'B'C',使△ABC与△A'B'C',满足上述条件中的一个或两个.你画出的△A'B'C'与△ABC一定全等吗 让学生按照下面给出的条件作出三角形. (1)三角形的两个角分别是30°、50°. (2)三角形的两条边分别是4cm,6cm. (3)三角形的一个角为30°,—条边为3cm.再通过画一画,剪一剪,比一比的方式,得出结论:只给出一个或两个条件时,都不能保证所画出的三角形一定全等. 探究二:先任意画出一个△A'B'C',使A'B'=AB,B'C'=BC,C'A'=CA,把画好的△A'B'C'剪下,放到△ABC上,它们全等吗 让学生充分交流后,在教师的引导下作出△A'B'C',并通过比较得出结论:三边对应相等的两个三角形全等.【例l】如下图△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证△ABD≌△ACD.让学生独立思考后口头表达理由,再让学生展示。师生共同检查学生展示内容,要特别强调证明格式的书写。【例2】如图,已知∠AOB,求作:∠A/O/B/,使∠A/O/B/=∠AOB。【教师点评】师生共同分析,探讨作图过程,让学生理解并掌握每一步的具体作法。 思考:为什么这样作出的∠A/O/B/和∠AOB是相等的。 让学生自己任意画一个角,巩固作图方法。三、新知巩固1、如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试.2、教材P37第1、2题。四、课堂小结:回顾反思本节课对知识的研究探索过程、小结方法及结论,提炼数学思想,掌握数学规律.例3 如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成两个相互全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试.五、作业1、课本P43练习第1题.2、.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 教学课题 12.2 三角形全等的判定(2) 课型
第3课时 主备教师 上课教师 审核人
学习目标 1、探索三角形全等条件之二:SAS,培养学生观察分析图形能力、动手能力.2、在探索三角形全等条件及其运用的过程中,体验操作、归纳得出数学结论的方法。
教学重点 难点 【重点】应用“边角边”证明两个三角形全等,进而得出线段或角相等.【难点】教学难点指导学生分析问题,寻找判定三角形全等的条件.
教 学 过 程 修改内容
一、预习导学:预习教材P37-39页,并尝试回答下列问题:多媒体出示探究3:已知任意△ABC,画△A'B'C',使A'B'=AB,A'C'=AC,∠A'=∠A.【教帅点拨】学生边学边画图,再让学生把画好的△A'B'C',剪下放在△ABC上,观察回答:1、通过对“探究三”的阅读理解,你得到了什么?2、通过对“例2”的阅读理解,你又得到了什么?3、继续阅读“探究四”,你有什么发现?根据前面的操作学习,鼓励学生用自己的语言来总结规律: 【两边和它们的夹角对应相等的两个三角形全等.(SAS)】 补充强调:角必须是两条相等的对应边的夹角,边必须是夹相等角的两对边.二、新知探究 合作交流出示例2,如图,有—池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么 让学生充分思考后,书写推理过程,并说明每一步的依据. (教师也可作如下分析: 要想证AB=DE, 只需证△ABC≌△DECABC与△DEC全等的条件现有_________还需要________________________)补充例题:1、已知:如图AB=AC,AD=AE,∠BAC=∠DAE 求证: △ABD≌△ACE证明:∵∠BAC=∠DAE(已知) ∠ BAC+ ∠ CAD= ∠DAE+ ∠ CAD ∴∠BAD=∠CAE 在△ABD与△ACE中 AB=AC(已知) ∠BAD= ∠CAE (已证) AD=AE(已知) ∴△ABD≌△ACE(SAS)变式一:求证:1.BD=CE 2. ∠B= ∠C 3. ∠ADB= ∠AEC【明确:证明分别属于两个三角形的线段相等或者角相等的问题,常常通过证明这两个三角形全等来解决.】三、再次探究,释解疑惑探究4,我们知道,两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗 为什么 让学生模仿前面的探究方法,得出结论:两边及其中一边的对角对应相等的两个三角形不一定全等. 四、巩固练习1、课本P39页,1、2.2、补充:已知:如图,AB⊥AC,AD⊥AE,AB=AC,AD=AE.
求证: △DAC≌△EABBE=DC ∠B= ∠ C ∠ D= ∠ E BE⊥CD五、课堂小结1.判定三角形全等的方法;2.证明线段、角相等常见的方法有哪些 让学生自由表述,其他学生补充,六、作业1.课本P43页,第2、3、4题.2.选作题:(1)小明做了一个如图所示的风筝,测得DE=DF,EH=FH,你能发现哪些结沦 并说明理由.(2)如图,∠1=∠2,AB=AD,AE=AC,求证BC=DE.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.2.3 三角形全等的条件(3) 课型 新授
第4课时 主备教师 上课教师 审核人
学习目标 1、掌握三角形全等的“角边角”“角角边”条件 2.能运用全等三角形的条件,解决简单的推理证明问题在探究中感受推理的魅力,在成功中获得喜悦,在分析中提升思维能力。
教学重点 难点 【重点】已知两角一边的三角形全等探究.【难点】灵活运用三角形全等条件证明
教 学 过 程 修改内容
一、提出问题,创设情境1.复习:(1)三角形中已知三个元素,包括哪几种情况? 三个角、三个边、两边一角、两角一边.(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?三种:①定义;②SSS;③SAS. 2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?二、新课讲解问题1:三角形中已知两角一边有几种可能? 1.两角和它们的夹边. 2.两角和其中一角的对边.问题2:三角形的两个内角分别是60°和80°,它们的夹边为4cm,你能画一个三角形同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是不是全等,你能得出什么规律? 将所得三角形重叠在一起,发现完全重合,这说明这些三角形全等.提炼规律:两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).问题3:我们刚才做的三角形是一个特殊三角形,画任意一个三角形ABC,能不能作一个△A′B′C′,使∠A=∠A′、∠B=∠B′、AB=A′B′呢?作法 ① 作线段A′B′,使A′B′=AB ② 分别以A′、B′为顶点,A′B′为一边在同一侧作∠DA′B′、∠EB′A,使∠D′AB=∠CAB,∠EB′A′=∠CBA. ③射线A′D与B′E交于一点,记为C′ 即可得到△A′B′C′. 将△A′B′C′与△ABC重 叠,发现两三角形全等.两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”). 思考:在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢? 问题4:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗? 证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180° ∠A=∠D,∠B=∠E ∴∠A+∠B=∠D+∠E ∴∠C=∠F 在△ABC和△DEF中 ∴△ABC≌△DEF(ASA). 两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”).5.探究:对于三个角对应相等的两个三角形全等吗?如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。三个角对应相等的两个三角形不一定全等 [例]如下图,D在AB上,E在AC上,AB=AC,∠B=∠C.求证:AD=AE. [分析]AD和AE分别在△ADC和△AEB中,所以要证AD=AE,只需证明△ADC≌△AEB即可.三、新知巩固 1.课本P13练习1、2.2.补充练习图中的两个三角形全等吗?请说明理由.四、课堂小结 我们有五种判定三角形全等的方法:【边边边(SSS) 边角边(SAS) 角边角(ASA) 角角边(AAS)】 推证两三角形全等时,要善于观察,寻求对应相等的条件,从而获得解题途径.五、作业 1.教材P44页 第4、7、8题.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.2 三角形全等的条件(4) 课型 新授
第5课时 主备教师 上课教师 审核人
学习目标 1、掌握直角三角形全等的条件,并能运用其解决一些实际问题2、经历探索Rt△全等条件的过程,体会利用操作、归纳获得数学结论的过程;
教学重点 难点 【重点】运用直角三角形全等的条件解决一些实际问题。【难点】熟练运用直角三角形全等的条件解决一些实际问题。
教 学 过 程 修改内容
一、预习导学:1、判定两个三角形全等的方法: 、 、 、 2、如图,Rt△ABC中,直角边是 、 , 斜边是 3、如图,AB⊥BE于C,DE⊥BE于E,(1)若∠A=∠D,AB=DE,则△ABC与△DEF _______根据 (用简写法)(2)若∠A=∠D,BC=EF,则△ABC与△DEF 根据 (用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF 根据 (用简写法)(4)若AB=DE,BC=EF,AC=DF则△ABC与△DEF 根据 (用简写法)二、新知探究探索练习:(动手操作): 已知线段a ,c (a
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.3 角的平分线的性质(1) 课型 新授
第6课时 主备教师 上课教师 审核人
学习目标 1、应用三角形全等的知识,解释角平分线的原理.2、会用尺规作一个已知角的平分线.3、角平分线的性质。
教学重点 难点 【重点】利用尺规作已知角的平分线.【难点】角的平分线的作图方法的提炼.
教 学 过 程 修改内容
一、预习导学: 生预习教材P48-49页,完成自主预习案。二、新知探究: 1. 议一议: 下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?即射线AC就是∠DAB的平分线.根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)2.作已知角的平分线的方法:已知: ∠AOB(如图)求作: ∠AOB的角平分线OC.作法:1、以O为圆心,适当长为半径作弧,交OA于M,交OB于N。2、分别以M、N为圆心,大于MN的长为半径作弧,两弧在∠AOB内部交于点C。3、作射线OC,射线OC即为所求。练一练:任意画一角∠AOB,作它的平分线.2、探究:下面用我们学过的知识证明发现:如图,已知AO平分∠BAC,OE⊥AB,OD⊥AC求证:OE=OD。让学生自己独立完成证明过程角平分线的性质定理:角平分线上的点到角的两边的距离相等数学语言:∵AO平分∠BOC,OE⊥AB,OD⊥OC ∴ OE=OD 如何更直观的表达题意?我们通常在证明之前画出图形,并用符号表示出已知与求证【补充例题】已知:如图,△ABC中 ∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上BD=DF,求证:CF=EB分析:要证CF=EB,首先我们想到的是要证它们所在的两个三角形全等,即Rt△CDF ≌ Rt△EDB. 现已有一个条件BD=DF(斜边相等),还需要我们找什么条件DC=DE (因为角的平分线的性质) 再用HL证明. 学生尝试完成证明过程。三、新知巩固课本P50第1题。 练后总结:平角∠AOB的平分线OC与直线AB垂直. 将OC反向延长得到直线CD,直线CD与AB也垂直.四、课时小结 本节课中我们利用已学过的三角形全等的知识,探究得到了角平分线仪器的操作原理, 由此归纳出角的平分线的尺规画法,并进一步探究到角平分线的性质.五、作业:1、教材P51第1、2题六、课后思考:思考:在一节数学课上,老师要求同学们练习一道题,题目的图形如图所示,图中的BD是∠ABC的平分线,在同学们忙于画图和分析题目时,小明同学忽然兴奋地大声说:“我有个发现!”原来他自己创造了一个在直角三角形中画锐角的平分线的方法.他的方法是这样的,在AB上取点E,使BE=BC,然后画DE⊥AB交AC于D,那么BD就是∠ABC的平分线.有的同学对小明的画法表示怀疑,你认为他的画法对不对呢?请你来说明理由.
教学反思
集体备课导学案
_年 月 日
学科 数学 年级 七 教学课题 12.3角的平分线的性质(2) 课型 新授
第7课时 主备教师 上课教师 审核人
学习目标 1、会叙述角的平分线的性质的逆定理“到角两边距离相等的点在角的平分线上”.2、能应用这个定理解决一些简单的实际问题.3、在操作中让学生经历了思考,仔细,合作,提升学生认真的习惯。
教学重点 难点 【重点】角平分线性质的逆定理及其应用.【难点】灵活应用两个性质解决问题.
教 学 过 程 修改内容
一、预习导学: 1、角的平分线性质定理的内容是什么?其中题设、结论是什么?2、角平分线性质定理的作用是证明什么?3、填空 如图:∵OC平分∠AOB, ∴AC=BC(角平分线性质定理)思考:怎样判定一个点是否在已知角的平分线上?二、新知探究:1、逆向思维探求角平分线的判定定理问: 把角平分线性质定理的题设、结论交换后,得出什么命题? 它正确?如何证明?指出:以上问题是我们今天所要解决的重点。2、证明上面提问得出的猜想:如果一个点到角的两边的距离相等,那么这个点在角的平分线上。已知:PD⊥OA于D,PE⊥OB于E,PD=PE求证:点P在∠AOB的平分线上分析: 直角△DOP≌直角△EOP证明:(学生板书)3、引导学生得出角平分线判定定理: 到一个角的两边的距离相等的点,在这个角的平分线上。【例题】现有一题目,两位同学分别用两种方法证明,问他们的做法正确?那一种方法好?已知:, CA⊥OA于A,BC⊥OB于B,AC=BC求证: OC平分∠AOB证法1:∵CA⊥OA,BC⊥OB∴∠A=∠B在△AOC和△BOC中∴△AOC≌△BOC(HL)∴∠AOC=∠BOC ∴OC平分∠AOB证法2:∵ CA⊥OA于A,BC⊥OB于B, AC=BC∴OC平分∠AOB(角平分线判定定理)指出:在已知一定条件下,证角平分线不再用三角形全等后角相等得出,可直接运用角平分线判定定理。三、新知巩固 1 、P 50 第2题 2 、完成当堂评价案四、小结 1、 角平分线的判定定理是什么?它的作用是用来证 明什么相等? 2、在已知一定条件下,证角平分线不再用三角形全等后角相等得出,可直接运用角平分线判定定理。五、作业 1如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠BAO=∠CAO2.已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD 求证:⑴△BDE≌△CDF ⑵点D在∠A的平分线上
教学反思
A
B
C
D
E
A
C
D
E
B
F
B
A
D
C
E
F
