11.2.1 三角形的内角和课件(共26张PPT)
文档属性
| 名称 | 11.2.1 三角形的内角和课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-27 21:55:00 | ||
图片预览





文档简介
(共26张PPT)
11.2.1 三角形的内角和
人教版八年级上册
知识回顾
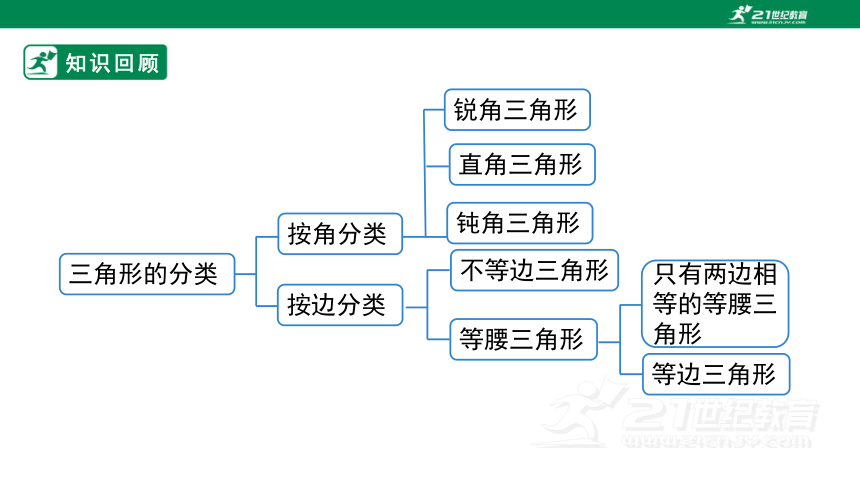
三角形的分类
按角分类
按边分类
不等边三角形
等腰三角形
只有两边相等的等腰三角形
等边三角形
锐角三角形
直角三角形
钝角三角形
教学目标
1.学习和掌握三角形的内角和定理.
2.理解三角形的内角和定理的推导、验证过程.
3.在解决实际问题时能熟练运用三角形的内角和定理.
新知导入
通过前面的学习,我们认识到三角形在生活中的广泛运用,并且学习了三角形边、高、中线、角平分线,这节课我们就来继续研究三角形的重要元素“内角”。
除了直角三角形和等边三角形具有固定度数的内角外,其他类型的三角形的内角度数都是可变化的,所以对于单独的一个内角度数,没有特别的规律,那么三角形的三个内角的和会不会有什么特别的规律呢?
新知探究
知识点 1
三角形的内角和
问题1:小学中我们学习过如何证明和计算一个三角形的内角和?
答:通过测量或者剪拼
问题2:测量是如何进行验证的?剪拼呢?还有其他方法吗?
测量法演示
剪拼法演示
折叠法演示
新知探究
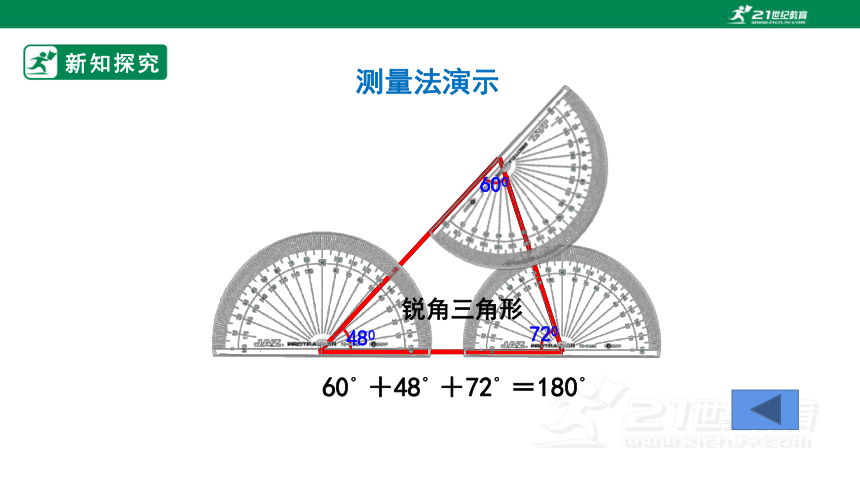
测量法演示
480
720
600
60°+48°+72°=180°
锐角三角形
新知探究
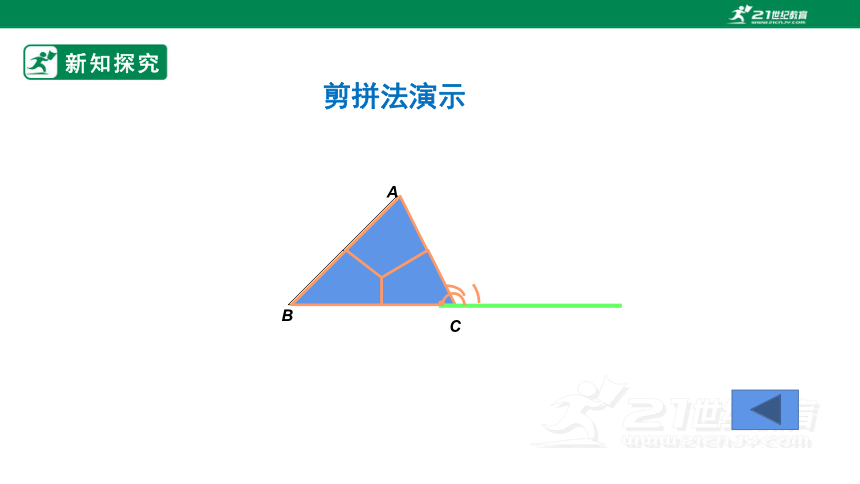
剪拼法演示
A
B
C
2
1
新知探究
折叠法演示
新知探究
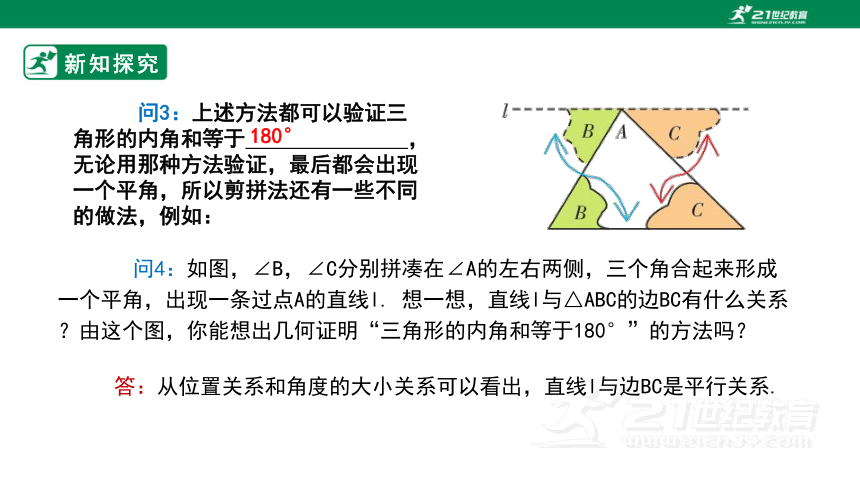
问3:上述方法都可以验证三角形的内角和等于 ,无论用那种方法验证,最后都会出现一个平角,所以剪拼法还有一些不同的做法,例如:
180°
问4:如图,∠B,∠C分别拼凑在∠A的左右两侧,三个角合起来形成一个平角,出现一条过点A的直线l. 想一想,直线l与△ABC的边BC有什么关系?由这个图,你能想出几何证明“三角形的内角和等于180°”的方法吗?
答:从位置关系和角度的大小关系可以看出,直线l与边BC是平行关系.
新知探究
已知:如图,△ABC,
求证:∠A+∠B+∠C=180°.
证明:过点A作直线l,使得l//BC.
∵l//BC,
∴∠2=∠B,∠3=∠C.
∵∠1、∠2、∠3构成平角,∴∠1+∠2+∠3=180°.
则∠BAC+∠B+∠C=180°.
三角形内角和定理的证明
你能想出来其他的证明方法吗?
2
3
1
新知探究
方法二 证明:过点C作直线l,使得l//AB,延长BC.∵l//AB,
∴∠2=∠A, ∠3=∠B.
∵∠1、∠2、∠3构成平角,
∴∠1+∠2+∠3=180°.
则∠ACB+∠A+∠B=180°.
如图,已知△ABC,求证∠A+∠B+∠C=180°.
A
C
1
3
2
l
B
新知探究
C
B
A
E
D
F
证法3:过BC上一点D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
新知小结
为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,通过作平行线,利用平行线的性质,把所证问题转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
新知典例
例1 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数.
解:∵∠BAC=40°,AD是△ABC的角平分线, ∴∠BAD=20°.
∵在△ADB中,∠B=75°,
∴∠ADB=180°-∠BAD-∠B=85°.
A
D
C
B
课堂练习
1. 如图,已知在△ABC中,∠B=30°,∠C=50°,AE是BC边上的高,AD是∠BAC的角平分线,求∠DAE的度数.
解:∵∠B=30°,∠C=50°,
∴∠BAC=180°﹣∠B﹣∠C=100°
∵AD是∠BAC的角平分线,
∴
∵AE是BC边上的高,
∴∠AEB=90°,
∴∠BAE=90°﹣∠B=60°,
∴∠DAE=∠BAE﹣∠BAD=10°
新知典例
例2 如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向. 从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB是多少度
A
B
C
D
北
北
E
解:∵∠CAB=∠BAD–∠CAD=80°–50°=30°,∵AD//BE得,∴∠BAD+∠ABE=180°,
∴∠ABE=180°–∠BAD=180°–80°=100°,
∴∠ABC=∠ABE–∠EBC=100°–40°=60°.
在△ABC中,∠ACB=180°–∠ABC–∠CAB=
180°–60°–30°=90°.
答:从B岛看A,C两岛的视角∠ABC是60度,从C岛看A,B两岛的视角∠ACB是90度.
课堂练习
2. 如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?
C
解:∵∠CAD=30°,∠ADC=90°,∴∠ACD=60°.
∵∠CBD=45°,∠ADC=90°,
∴∠BCD=45°.
∴∠ACB=∠ACD-∠BCD=15°.
课堂小测
1.如图,∠B=30°,∠CAD=65°且AD平分∠CAE,则∠ACD等于( )
A.95° B.65° C.50° D.80°
解:∵∠CAD=65°,AD平分∠CAE,
∴∠CAE=2∠CAD=130°,
∴∠BAC=180°﹣130°=50°,
∵∠B=30°,
∴∠ACD=∠B+∠BAC=30°+50°=80°
D
课堂小测
2.如图,在△ABC中,CD是∠ACB的角平分线交AB于点D,DE∥BC,交AC于点E,∠A=60°,∠BDC=80°,则∠EDC的度数为( )
A.10° B.20° C.30° D.40°
解:∵CD是∠ACB的角平分线,
∴∠BCD=∠ACD.
∵∠BDC=∠A+∠ACD,
∴80°=60°+∠ACD.
∴∠ACD=∠BCD=20°.
∵DE∥BC,
∴∠EDC=∠BCD=20°.
B
课堂小测
3.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为 °.
130
解:∵∠B=50°,∠CEB=∠ADB﹣90°,
∴∠EHD=180°﹣50°=130°,
又∵∠EHD=∠AHC,
∴∠AHC=130°
课堂小测
4.如图,将直角三角板ABC与直尺贴在一起,使三角板ABC的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=65°,则∠2的度数等于 .
25°
解:如图,由于直尺的两条边是平行线,
∴∠1=∠3,
∵∠ACB=90°=∠2+∠3,
∴∠1+∠2=90°,
∴∠2=90°﹣∠1=90°﹣65°=25°,
课堂小测
5.已知如图,AD是△ABC的角平分线,点D、E在BC上,点G在CA的延长线上,EG交AB于点F,且∠BEF+∠ADC=180°.∠AFG与∠G相等吗?为什么?
解:∠AFG=∠G,证明如下:
∵∠BEF+∠ADC=180°(已知),
∠BEF+∠GED=180°(平角的定义),
∴∠GED=∠ADC(同角的补角相等).
∴AD∥GE(同位角相等,两直线平行),
∴∠AFG=∠BAD(两直线平行,内错角相等),
∠G=∠CAD(两直线平行,同位角相等),
∵AD是∠BAC的平分线(已知),
∴∠BAD=∠CAD(角平分线的定义),
∴∠AFG=∠G(等量代换).
课堂总结
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.1 三角形的内角和
人教版八年级上册
知识回顾
三角形的分类
按角分类
按边分类
不等边三角形
等腰三角形
只有两边相等的等腰三角形
等边三角形
锐角三角形
直角三角形
钝角三角形
教学目标
1.学习和掌握三角形的内角和定理.
2.理解三角形的内角和定理的推导、验证过程.
3.在解决实际问题时能熟练运用三角形的内角和定理.
新知导入
通过前面的学习,我们认识到三角形在生活中的广泛运用,并且学习了三角形边、高、中线、角平分线,这节课我们就来继续研究三角形的重要元素“内角”。
除了直角三角形和等边三角形具有固定度数的内角外,其他类型的三角形的内角度数都是可变化的,所以对于单独的一个内角度数,没有特别的规律,那么三角形的三个内角的和会不会有什么特别的规律呢?
新知探究
知识点 1
三角形的内角和
问题1:小学中我们学习过如何证明和计算一个三角形的内角和?
答:通过测量或者剪拼
问题2:测量是如何进行验证的?剪拼呢?还有其他方法吗?
测量法演示
剪拼法演示
折叠法演示
新知探究
测量法演示
480
720
600
60°+48°+72°=180°
锐角三角形
新知探究
剪拼法演示
A
B
C
2
1
新知探究
折叠法演示
新知探究
问3:上述方法都可以验证三角形的内角和等于 ,无论用那种方法验证,最后都会出现一个平角,所以剪拼法还有一些不同的做法,例如:
180°
问4:如图,∠B,∠C分别拼凑在∠A的左右两侧,三个角合起来形成一个平角,出现一条过点A的直线l. 想一想,直线l与△ABC的边BC有什么关系?由这个图,你能想出几何证明“三角形的内角和等于180°”的方法吗?
答:从位置关系和角度的大小关系可以看出,直线l与边BC是平行关系.
新知探究
已知:如图,△ABC,
求证:∠A+∠B+∠C=180°.
证明:过点A作直线l,使得l//BC.
∵l//BC,
∴∠2=∠B,∠3=∠C.
∵∠1、∠2、∠3构成平角,∴∠1+∠2+∠3=180°.
则∠BAC+∠B+∠C=180°.
三角形内角和定理的证明
你能想出来其他的证明方法吗?
2
3
1
新知探究
方法二 证明:过点C作直线l,使得l//AB,延长BC.∵l//AB,
∴∠2=∠A, ∠3=∠B.
∵∠1、∠2、∠3构成平角,
∴∠1+∠2+∠3=180°.
则∠ACB+∠A+∠B=180°.
如图,已知△ABC,求证∠A+∠B+∠C=180°.
A
C
1
3
2
l
B
新知探究
C
B
A
E
D
F
证法3:过BC上一点D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
新知小结
为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,通过作平行线,利用平行线的性质,把所证问题转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
新知典例
例1 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数.
解:∵∠BAC=40°,AD是△ABC的角平分线, ∴∠BAD=20°.
∵在△ADB中,∠B=75°,
∴∠ADB=180°-∠BAD-∠B=85°.
A
D
C
B
课堂练习
1. 如图,已知在△ABC中,∠B=30°,∠C=50°,AE是BC边上的高,AD是∠BAC的角平分线,求∠DAE的度数.
解:∵∠B=30°,∠C=50°,
∴∠BAC=180°﹣∠B﹣∠C=100°
∵AD是∠BAC的角平分线,
∴
∵AE是BC边上的高,
∴∠AEB=90°,
∴∠BAE=90°﹣∠B=60°,
∴∠DAE=∠BAE﹣∠BAD=10°
新知典例
例2 如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向. 从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB是多少度
A
B
C
D
北
北
E
解:∵∠CAB=∠BAD–∠CAD=80°–50°=30°,∵AD//BE得,∴∠BAD+∠ABE=180°,
∴∠ABE=180°–∠BAD=180°–80°=100°,
∴∠ABC=∠ABE–∠EBC=100°–40°=60°.
在△ABC中,∠ACB=180°–∠ABC–∠CAB=
180°–60°–30°=90°.
答:从B岛看A,C两岛的视角∠ABC是60度,从C岛看A,B两岛的视角∠ACB是90度.
课堂练习
2. 如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?
C
解:∵∠CAD=30°,∠ADC=90°,∴∠ACD=60°.
∵∠CBD=45°,∠ADC=90°,
∴∠BCD=45°.
∴∠ACB=∠ACD-∠BCD=15°.
课堂小测
1.如图,∠B=30°,∠CAD=65°且AD平分∠CAE,则∠ACD等于( )
A.95° B.65° C.50° D.80°
解:∵∠CAD=65°,AD平分∠CAE,
∴∠CAE=2∠CAD=130°,
∴∠BAC=180°﹣130°=50°,
∵∠B=30°,
∴∠ACD=∠B+∠BAC=30°+50°=80°
D
课堂小测
2.如图,在△ABC中,CD是∠ACB的角平分线交AB于点D,DE∥BC,交AC于点E,∠A=60°,∠BDC=80°,则∠EDC的度数为( )
A.10° B.20° C.30° D.40°
解:∵CD是∠ACB的角平分线,
∴∠BCD=∠ACD.
∵∠BDC=∠A+∠ACD,
∴80°=60°+∠ACD.
∴∠ACD=∠BCD=20°.
∵DE∥BC,
∴∠EDC=∠BCD=20°.
B
课堂小测
3.如图,在△ABC中,AD⊥BC,CE⊥AB,且AD与CE交于点H,若∠B=50°,则∠AHC的度数为 °.
130
解:∵∠B=50°,∠CEB=∠ADB﹣90°,
∴∠EHD=180°﹣50°=130°,
又∵∠EHD=∠AHC,
∴∠AHC=130°
课堂小测
4.如图,将直角三角板ABC与直尺贴在一起,使三角板ABC的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=65°,则∠2的度数等于 .
25°
解:如图,由于直尺的两条边是平行线,
∴∠1=∠3,
∵∠ACB=90°=∠2+∠3,
∴∠1+∠2=90°,
∴∠2=90°﹣∠1=90°﹣65°=25°,
课堂小测
5.已知如图,AD是△ABC的角平分线,点D、E在BC上,点G在CA的延长线上,EG交AB于点F,且∠BEF+∠ADC=180°.∠AFG与∠G相等吗?为什么?
解:∠AFG=∠G,证明如下:
∵∠BEF+∠ADC=180°(已知),
∠BEF+∠GED=180°(平角的定义),
∴∠GED=∠ADC(同角的补角相等).
∴AD∥GE(同位角相等,两直线平行),
∴∠AFG=∠BAD(两直线平行,内错角相等),
∠G=∠CAD(两直线平行,同位角相等),
∵AD是∠BAC的平分线(已知),
∴∠BAD=∠CAD(角平分线的定义),
∴∠AFG=∠G(等量代换).
课堂总结
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
