人教A版2019必修第一册5.1 任意角和弧度制 精品学案(Word版含答案)
文档属性
| 名称 | 人教A版2019必修第一册5.1 任意角和弧度制 精品学案(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 06:12:33 | ||
图片预览


文档简介
5.1 任意角和弧度制
目标导航
1.了解任意角的概念,区分正角、负角与零角.
2.了解象限角的概念.
3.理解并掌握终边相同的角的概念,能写出终边相同的角所组成的集合.
4.了解弧度制下,角的集合与实数集之间的一一对应关系.
5.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数.
知识解读
知识点一 任意角
1.角的概念:
角可以看成平面内一条 绕着它的端点 所成的 .
2.角的表示:
如图所示:角α可记为“α”或“∠α”或“∠AOB”,始边: ,终边: ,顶点 .
3.角的分类:
名称 定义 图示
正角 一条射线绕其端点按 方向旋转形成的角
负角 一条射线绕其端点按 方向旋转形成的角
零角 一条射线 做任何旋转形成的角
知识点二 角的加法与减法
设α,β是任意两个角, 为角α的相反角.
(1)α+β:把角α的 旋转角β.
(2)α-β:α-β= .
知识点三 象限角
把角放在平面直角坐标系中,使角的顶点与 重合,角的始边与x轴的非负半轴重合,那么,角的 在第几象限,就说这个角是第几 ;如果角的终边在 ,就认为这个角不属于任何一个象限.
知识点四 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
知识点五 度量角的两种制度
角度制 定义 用度作为单位来度量角的单位制
1度的角 1度的角等于周角的
弧度制 定义 以 作为单位来度量角的单位制
1弧度的角 长度等于 的圆弧所对的圆心角
知识点六 弧度数的计算
(1)弧度数
正角的弧度数是一个 数.
负角的弧度数是一个 数.
(2)零角的弧度数是
(3)弧度数的计算
公式:
知识点七 角度与弧度的互化
角度化弧度 弧度化角度
360°= rad 2π rad=
180°= rad π rad=
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
度数×=弧度数 弧度数×°=度数
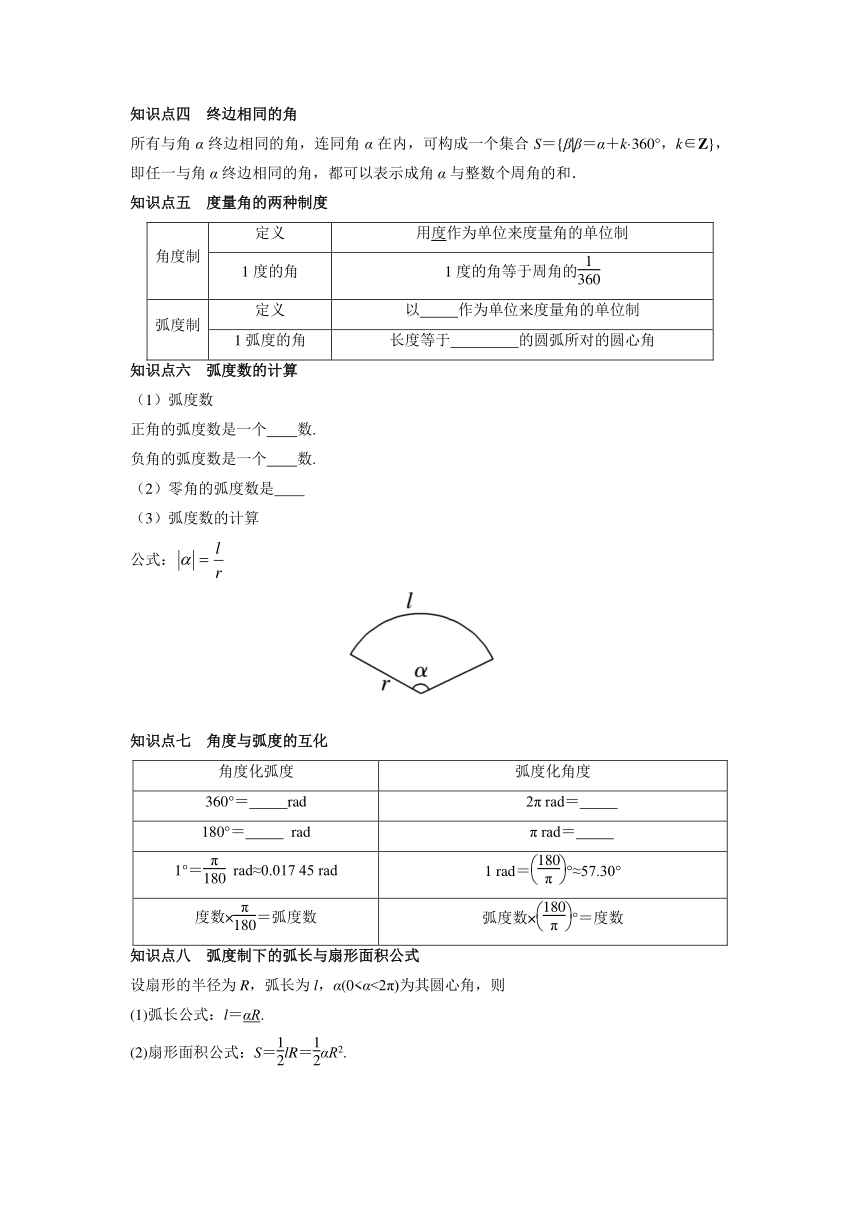
知识点八 弧度制下的弧长与扇形面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l=αR.
(2)扇形面积公式:S=lR=αR2.
跟踪训练
1.与终边相同的角是( )
A. B. C. D.
2.的角化为弧度制的结果为( )
A. B. C. D.
3.下列说法正确的是( )
A.终边相同的角相等 B.相等的角终边相同
C.小于的角是锐角 D.第一象限的角是正角
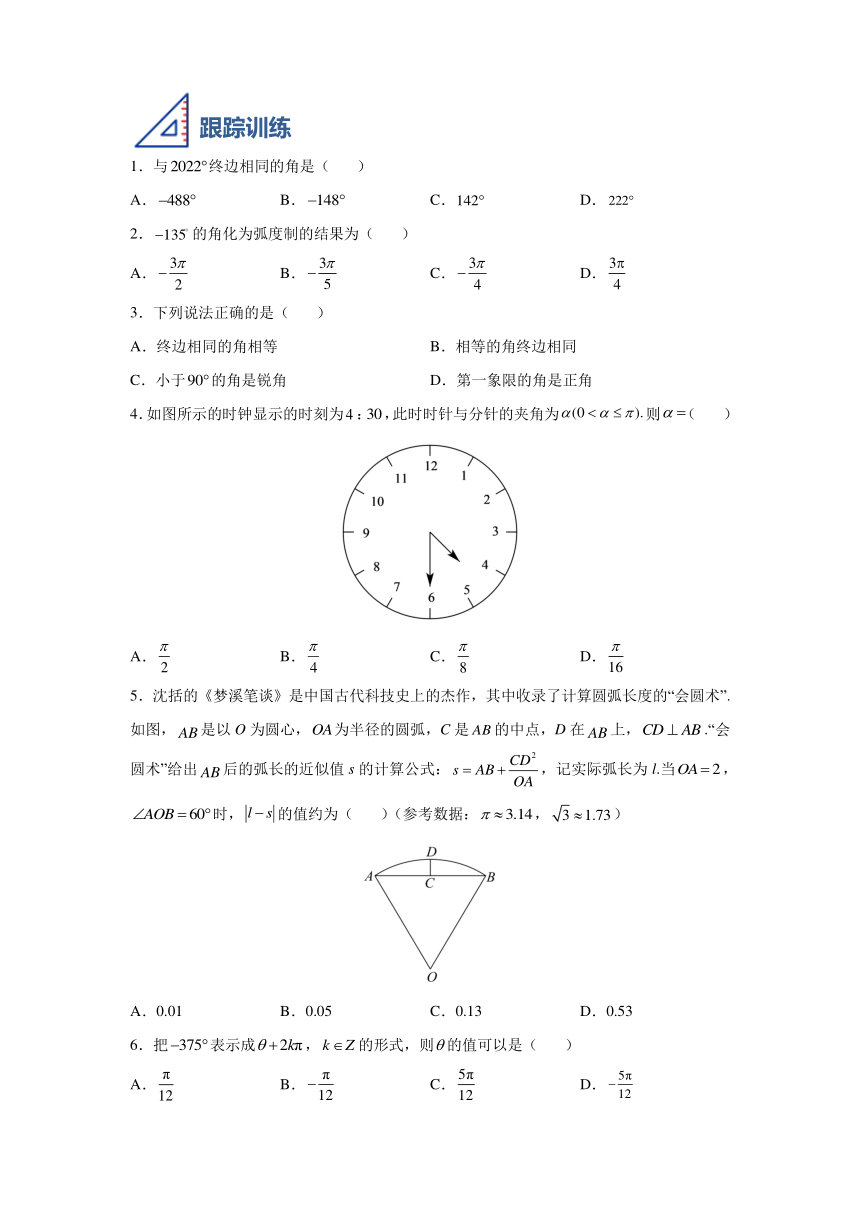
4.如图所示的时钟显示的时刻为:,此时时针与分针的夹角为则( )
A. B. C. D.
5.沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以O为圆心,为半径的圆弧,C是的中点,D在上,.“会圆术”给出后的弧长的近似值s的计算公式:,记实际弧长为l.当,时,的值约为( )(参考数据:,)
A.0.01 B.0.05 C.0.13 D.0.53
6.把表示成,的形式,则的值可以是( )
A. B. C. D.
7.角所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知一扇形的周长为,则当该扇形的面积取得最大时,圆心角大小为( )
A. B. C.1 D.2
二、多选题
9.若是第二象限角,则( )
A.是第一象限角 B.是第一或第三象限角
C.是第二象限角 D.是第三或第四象限角
10.设扇形的圆心角为,半径为,弧长为,面积为,周长为,则( )
A.若,确定,则,唯一确定 B.若,确定,则,唯一确定
C.若,确定,则,唯一确定 D.若,确定,则,唯一确定
11.下列结论中正确的是( )
A.终边经过点的角的集合是;
B.将表的分针拨慢10分钟,则分针转过的角的弧度数是;
C.若是第三象限角,则是第二象限角,为第一或第二象限角;
D.,,则
12.已知{第一象限角},{锐角},{小于的角},那么A、B、C关系是( )
A. B. C. D.
三、填空题
13.写出两个与终边相同的角______.
14.半径为2cm,中心角为的扇形的弧长为______cm.
15.如图,扇环ABCD中,弧,弧,,则扇环ABCD的面积__________.
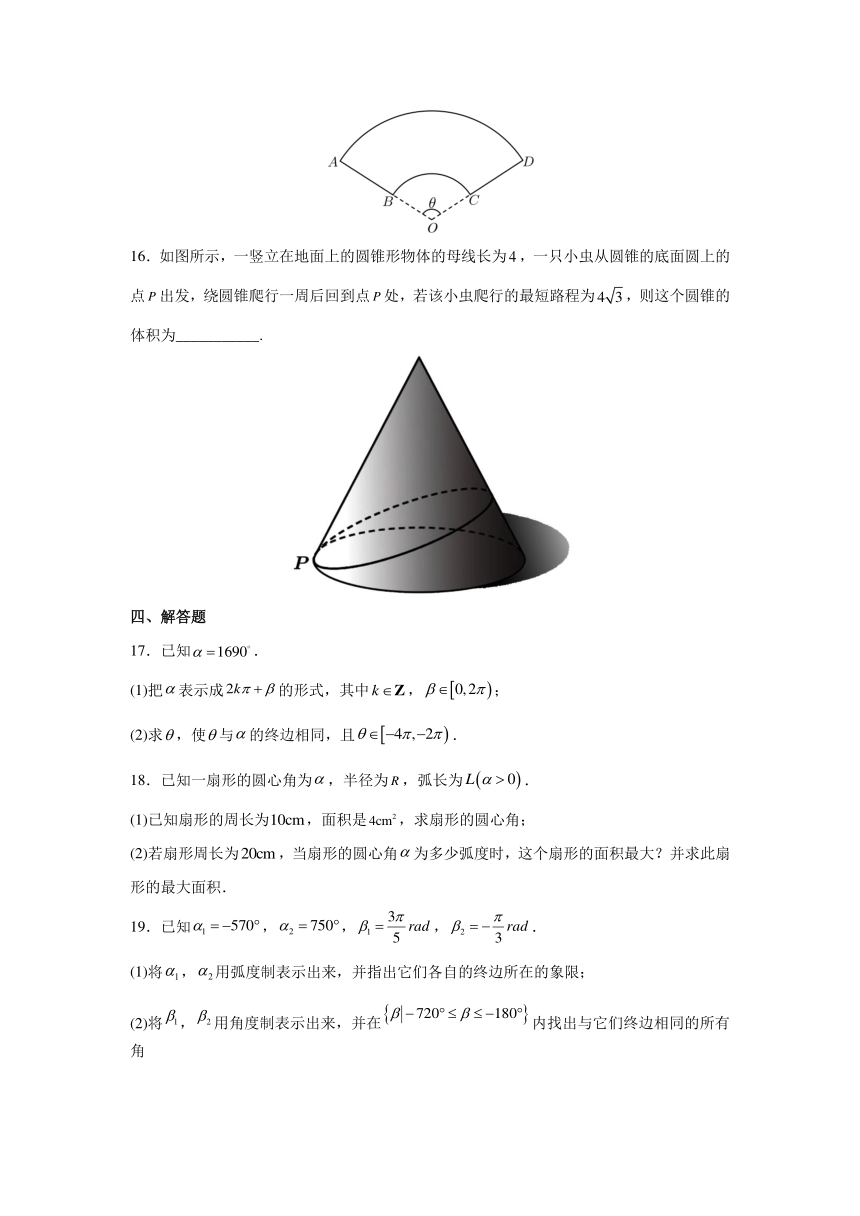
16.如图所示,一竖立在地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥爬行一周后回到点处,若该小虫爬行的最短路程为,则这个圆锥的体积为___________.
四、解答题
17.已知.
(1)把表示成的形式,其中,;
(2)求,使与的终边相同,且.
18.已知一扇形的圆心角为,半径为,弧长为.
(1)已知扇形的周长为,面积是,求扇形的圆心角;
(2)若扇形周长为,当扇形的圆心角为多少弧度时,这个扇形的面积最大?并求此扇形的最大面积.
19.已知,,,.
(1)将,用弧度制表示出来,并指出它们各自的终边所在的象限;
(2)将,用角度制表示出来,并在内找出与它们终边相同的所有角
5.1 任意角和弧度制
目标导航
1.了解任意角的概念,区分正角、负角与零角.
2.了解象限角的概念.
3.理解并掌握终边相同的角的概念,能写出终边相同的角所组成的集合.
4.了解弧度制下,角的集合与实数集之间的一一对应关系.
5.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数.
知识解读
知识点一 任意角
1.角的概念:
角可以看成平面内一条 绕着它的端点 所成的 .
2.角的表示:
如图所示:角α可记为“α”或“∠α”或“∠AOB”,始边: ,终边: ,顶点 .
3.角的分类:
名称 定义 图示
正角 一条射线绕其端点按 方向旋转形成的角
负角 一条射线绕其端点按 方向旋转形成的角
零角 一条射线 做任何旋转形成的角
【答案】射线 旋转 图形 OA OB O 逆时针 顺时针 没有
知识点二 角的加法与减法
设α,β是任意两个角, 为角α的相反角.
(1)α+β:把角α的 旋转角β.
(2)α-β:α-β= .
【答案】-α 终边 α+(-β)
知识点三 象限角
把角放在平面直角坐标系中,使角的顶点与 重合,角的始边与x轴的非负半轴重合,那么,角的 在第几象限,就说这个角是第几 ;如果角的终边在 ,就认为这个角不属于任何一个象限.
【答案】原点 终边 象限角 坐标轴上
知识点四 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
知识点五 度量角的两种制度
角度制 定义 用度作为单位来度量角的单位制
1度的角 1度的角等于周角的
弧度制 定义 以 作为单位来度量角的单位制
1弧度的角 长度等于 的圆弧所对的圆心角
【答案】弧度 半径长
知识点六 弧度数的计算
(1)弧度数
正角的弧度数是一个 数.
负角的弧度数是一个 数.
(2)零角的弧度数是
(3)弧度数的计算
公式:
【答案】正 负 0
知识点七 角度与弧度的互化
角度化弧度 弧度化角度
360°= rad 2π rad=
180°= rad π rad=
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
度数×=弧度数 弧度数×°=度数
【答案】2π 360° π 180°
知识点八 弧度制下的弧长与扇形面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l=αR.
(2)扇形面积公式:S=lR=αR2.
跟踪训练
1.与终边相同的角是( )
A. B. C. D.
【答案】D
【分析】与终边相同的角可表示为.
【详解】∵,
∴与终边相同的角是.
故选:D
2.的角化为弧度制的结果为( )
A. B. C. D.
【答案】C
【分析】根据角度和弧度的换算公式即可得到答案.
【详解】.
故选:C.
3.下列说法正确的是( )
A.终边相同的角相等 B.相等的角终边相同
C.小于的角是锐角 D.第一象限的角是正角
【答案】B
【分析】根据角的定义判断.
【详解】终边相同的角相差周角的整数倍,A不正确;相等的角终边一定相同;所以B正确;小于的角是锐角可以是负角,C错;第一象限的角是正角,也可以是负角,D错误.
故选:B.
4.如图所示的时钟显示的时刻为:,此时时针与分针的夹角为则( )
A. B. C. D.
【答案】B
【分析】由图可知为周角的,计算可得结果.
【详解】解:由图可知,.
故选:B.
5.沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以O为圆心,为半径的圆弧,C是的中点,D在上,.“会圆术”给出后的弧长的近似值s的计算公式:,记实际弧长为l.当,时,的值约为( )(参考数据:,)
A.0.01 B.0.05 C.0.13 D.0.53
【答案】D
【分析】根据题意求出与的值,代入弧长公式和求出和即可.
【详解】因为,所以,
因为是的中点,在上,,
所以延长可得在上,,
所以,
,
所以.
故选:D
6.把表示成,的形式,则的值可以是( )
A. B. C. D.
【答案】B
【分析】由结合弧度制求解即可.
【详解】∵,∴
故选:B
7.角所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【分析】根据角的终边位置可直接得到结果.
【详解】,角位于第三象限.
故选:C.
8.已知一扇形的周长为,则当该扇形的面积取得最大时,圆心角大小为( )
A. B. C.1 D.2
【答案】D
【分析】根据周长建立弧长与半径间的关系,由扇形面积公式可得,利用二次函数求最值,并求出S最大时对应的圆心角即可.
【详解】设扇形的半径为,弧长为,则,
所以,
扇形面积,
当时,有最大值,此时圆心角,
故选:D
二、多选题
9.若是第二象限角,则( )
A.是第一象限角 B.是第一或第三象限角
C.是第二象限角 D.是第三或第四象限角
【答案】AB
【分析】由与关于轴对称,即可判断AD;由已知可得,,再根据不等式的性质可判断B;由是第一象限角判断C.
【详解】解:因为与关于轴对称,而是第二象限角,所以是第三象限角,
所以是第一象限角,故A正确,D错误;
因为是第二象限角,所以,,所以,,
故是第一或第三象限角,故 B正确;
因为是第二象限角,所以是第一象限角,故C错误.
故选:AB.
10.设扇形的圆心角为,半径为,弧长为,面积为,周长为,则( )
A.若,确定,则,唯一确定 B.若,确定,则,唯一确定
C.若,确定,则,唯一确定 D.若,确定,则,唯一确定
【答案】ABD
【分析】由弧长公式和面积公式判断.
【详解】由弧长公式得,,周长,
若,确定,则唯一确定,则,唯一确定,故A正确,
若,确定,则唯一确定,则,唯一确定,故B正确,
若,确定,则,,即,当,有两正实根,不唯一确定,所以,不一定唯一确定,故C错误,
若,确定,则唯一确定,则唯一确定,故D正确,
故选:ABD.
11.下列结论中正确的是( )
A.终边经过点的角的集合是;
B.将表的分针拨慢10分钟,则分针转过的角的弧度数是;
C.若是第三象限角,则是第二象限角,为第一或第二象限角;
D.,,则
【答案】ABD
【分析】直接以角的表示方法,象限角的概念,集合间的关系求出结果.
【详解】A.终边经过点的角的终边在第一象限平分线上,故角的集合是,所以A正确;
B. 将表的分针拨慢10分钟,按逆时针旋转,则分针转过的角度为,对应弧度数是,所以B正确;
C.因为是第三象限角,即,所以,当为奇数时,是第四象限角,当为偶数时,是第二象限角;,所以的终边位置在第一或第二象限或轴非负半轴,所以C错误;
D. ,
,易知,所以D正确;
故选:ABD.
12.已知{第一象限角},{锐角},{小于的角},那么A、B、C关系是( )
A. B. C. D.
【答案】BC
【解析】根据集合中角的范围,对选项逐一分析,由此得出正确选项.
【详解】对于A选项,除了锐角,还包括其它角,比如,所以A选项错误.
对于B选项,锐角是小于的角,故B选项正确.
对于C选项,锐角是第一象限角,故C选项正确.
对于D选项,中角的范围不一样,所以D选项错误.
故选:BC
【点睛】本小题主要考查角的范围比较,考查集合交集、并集和集合相等的概念,属于基础题.
三、填空题
13.写出两个与终边相同的角______.
【答案】,(答案不唯一)
【分析】利用终边相同的角的定义求解.
【详解】设是与终边相同的角,
则,
令,得,
令,得,
故答案为:,(其他正确答案也可)14.半径为2cm,中心角为的扇形的弧长为______cm.
【答案】
【分析】先将圆心角角度化成弧度制,然后直接利用弧长公式进行求解即可.
【详解】解:圆弧所对的中心角为即为弧度,半径为
弧长为.
故答案为:.
15.如图,扇环ABCD中,弧,弧,,则扇环ABCD的面积__________.
【答案】3
【分析】根据弧长公式求出,,再由根据扇形的面积公式求解即可.
【详解】设,
因为弧,弧,,
所以,,
所以,,
又扇形的面积为,扇形的面积为,
所以扇环ABCD的面积.
故答案为:3
16.如图所示,一竖立在地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥爬行一周后回到点处,若该小虫爬行的最短路程为,则这个圆锥的体积为___________.
【答案】
【分析】作出该圆锥的侧面展开图,该小虫爬行的最短路程为PP′,由余弦定理求出,求出底面圆的半径r,从而求出这个圆锥的高,由此能求出这个圆锥的体积.
【详解】作出该圆锥的侧面展开图,如图所示:
该小虫爬行的最短路程为PP′,由余弦定理可得:
∴.
设底面圆的半径为r,则有,解得,
所以这个圆锥的高为,
则这个圆锥的体积为.
故答案为:.
【点睛】立体几何中的翻折叠(展开)问题要注意翻折(展开)过程中的不变量.
四、解答题
17.已知.
(1)把表示成的形式,其中,;
(2)求,使与的终边相同,且.
【答案】(1)
(2)
【分析】(1)将直接表示为的形式,其中,;
(2)设,由可求得的值,即可得解.
【解析】(1)解:.
(2)解:,设,
由可得,解得,
,则,故.
18.已知一扇形的圆心角为,半径为,弧长为.
(1)已知扇形的周长为,面积是,求扇形的圆心角;
(2)若扇形周长为,当扇形的圆心角为多少弧度时,这个扇形的面积最大?并求此扇形的最大面积.
【答案】(1)
(2)取得最大值25,此时
【分析】(1)根据弧长公式及扇形的面积公式,再结合扇形的周长公式即可求解;
(2)根据扇形的周长公式及扇形的面积公式,再结合二次函数的性质即可求解.
【解析】(1)由题意得,解得(舍去),.
所以扇形圆心角.
(2)由已知得,.
所以,
所以当时,取得最大值25,
,解得.
当扇形的圆心角为多少弧度时,这个扇形的面积最大为25.
19.已知,,,.
(1)将,用弧度制表示出来,并指出它们各自的终边所在的象限;
(2)将,用角度制表示出来,并在内找出与它们终边相同的所有角.
【答案】(1),第二象限;,第一象限
(2),和;,
【分析】(1)直接将角度转化成弧度表示即可;通过周期公式化简,可求出终边对应象限;
(2)将弧度转化成角度即可;通过任意角概念给赋值,求出在内对应角即可.
(1)由题意,根据角度制与弧度制的互化公式,可得
,
.
又由,所以与角的终边相同,所以终边位于第二象限;
,所以与角的终边相同,所以终边位于第一象限;
(2)根据角度制与弧度制的互化公式,可得,.
根据终边相同角的表示,可得与终边相同的角为,,当时,;当时,.
与终边相同的角为,,
当时,.
因此,在内,与终边相同的角是和,与终边相同的角是
目标导航
1.了解任意角的概念,区分正角、负角与零角.
2.了解象限角的概念.
3.理解并掌握终边相同的角的概念,能写出终边相同的角所组成的集合.
4.了解弧度制下,角的集合与实数集之间的一一对应关系.
5.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数.
知识解读
知识点一 任意角
1.角的概念:
角可以看成平面内一条 绕着它的端点 所成的 .
2.角的表示:
如图所示:角α可记为“α”或“∠α”或“∠AOB”,始边: ,终边: ,顶点 .
3.角的分类:
名称 定义 图示
正角 一条射线绕其端点按 方向旋转形成的角
负角 一条射线绕其端点按 方向旋转形成的角
零角 一条射线 做任何旋转形成的角
知识点二 角的加法与减法
设α,β是任意两个角, 为角α的相反角.
(1)α+β:把角α的 旋转角β.
(2)α-β:α-β= .
知识点三 象限角
把角放在平面直角坐标系中,使角的顶点与 重合,角的始边与x轴的非负半轴重合,那么,角的 在第几象限,就说这个角是第几 ;如果角的终边在 ,就认为这个角不属于任何一个象限.
知识点四 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
知识点五 度量角的两种制度
角度制 定义 用度作为单位来度量角的单位制
1度的角 1度的角等于周角的
弧度制 定义 以 作为单位来度量角的单位制
1弧度的角 长度等于 的圆弧所对的圆心角
知识点六 弧度数的计算
(1)弧度数
正角的弧度数是一个 数.
负角的弧度数是一个 数.
(2)零角的弧度数是
(3)弧度数的计算
公式:
知识点七 角度与弧度的互化
角度化弧度 弧度化角度
360°= rad 2π rad=
180°= rad π rad=
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
度数×=弧度数 弧度数×°=度数
知识点八 弧度制下的弧长与扇形面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l=αR.
(2)扇形面积公式:S=lR=αR2.
跟踪训练
1.与终边相同的角是( )
A. B. C. D.
2.的角化为弧度制的结果为( )
A. B. C. D.
3.下列说法正确的是( )
A.终边相同的角相等 B.相等的角终边相同
C.小于的角是锐角 D.第一象限的角是正角
4.如图所示的时钟显示的时刻为:,此时时针与分针的夹角为则( )
A. B. C. D.
5.沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以O为圆心,为半径的圆弧,C是的中点,D在上,.“会圆术”给出后的弧长的近似值s的计算公式:,记实际弧长为l.当,时,的值约为( )(参考数据:,)
A.0.01 B.0.05 C.0.13 D.0.53
6.把表示成,的形式,则的值可以是( )
A. B. C. D.
7.角所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知一扇形的周长为,则当该扇形的面积取得最大时,圆心角大小为( )
A. B. C.1 D.2
二、多选题
9.若是第二象限角,则( )
A.是第一象限角 B.是第一或第三象限角
C.是第二象限角 D.是第三或第四象限角
10.设扇形的圆心角为,半径为,弧长为,面积为,周长为,则( )
A.若,确定,则,唯一确定 B.若,确定,则,唯一确定
C.若,确定,则,唯一确定 D.若,确定,则,唯一确定
11.下列结论中正确的是( )
A.终边经过点的角的集合是;
B.将表的分针拨慢10分钟,则分针转过的角的弧度数是;
C.若是第三象限角,则是第二象限角,为第一或第二象限角;
D.,,则
12.已知{第一象限角},{锐角},{小于的角},那么A、B、C关系是( )
A. B. C. D.
三、填空题
13.写出两个与终边相同的角______.
14.半径为2cm,中心角为的扇形的弧长为______cm.
15.如图,扇环ABCD中,弧,弧,,则扇环ABCD的面积__________.
16.如图所示,一竖立在地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥爬行一周后回到点处,若该小虫爬行的最短路程为,则这个圆锥的体积为___________.
四、解答题
17.已知.
(1)把表示成的形式,其中,;
(2)求,使与的终边相同,且.
18.已知一扇形的圆心角为,半径为,弧长为.
(1)已知扇形的周长为,面积是,求扇形的圆心角;
(2)若扇形周长为,当扇形的圆心角为多少弧度时,这个扇形的面积最大?并求此扇形的最大面积.
19.已知,,,.
(1)将,用弧度制表示出来,并指出它们各自的终边所在的象限;
(2)将,用角度制表示出来,并在内找出与它们终边相同的所有角
5.1 任意角和弧度制
目标导航
1.了解任意角的概念,区分正角、负角与零角.
2.了解象限角的概念.
3.理解并掌握终边相同的角的概念,能写出终边相同的角所组成的集合.
4.了解弧度制下,角的集合与实数集之间的一一对应关系.
5.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数.
知识解读
知识点一 任意角
1.角的概念:
角可以看成平面内一条 绕着它的端点 所成的 .
2.角的表示:
如图所示:角α可记为“α”或“∠α”或“∠AOB”,始边: ,终边: ,顶点 .
3.角的分类:
名称 定义 图示
正角 一条射线绕其端点按 方向旋转形成的角
负角 一条射线绕其端点按 方向旋转形成的角
零角 一条射线 做任何旋转形成的角
【答案】射线 旋转 图形 OA OB O 逆时针 顺时针 没有
知识点二 角的加法与减法
设α,β是任意两个角, 为角α的相反角.
(1)α+β:把角α的 旋转角β.
(2)α-β:α-β= .
【答案】-α 终边 α+(-β)
知识点三 象限角
把角放在平面直角坐标系中,使角的顶点与 重合,角的始边与x轴的非负半轴重合,那么,角的 在第几象限,就说这个角是第几 ;如果角的终边在 ,就认为这个角不属于任何一个象限.
【答案】原点 终边 象限角 坐标轴上
知识点四 终边相同的角
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
知识点五 度量角的两种制度
角度制 定义 用度作为单位来度量角的单位制
1度的角 1度的角等于周角的
弧度制 定义 以 作为单位来度量角的单位制
1弧度的角 长度等于 的圆弧所对的圆心角
【答案】弧度 半径长
知识点六 弧度数的计算
(1)弧度数
正角的弧度数是一个 数.
负角的弧度数是一个 数.
(2)零角的弧度数是
(3)弧度数的计算
公式:
【答案】正 负 0
知识点七 角度与弧度的互化
角度化弧度 弧度化角度
360°= rad 2π rad=
180°= rad π rad=
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
度数×=弧度数 弧度数×°=度数
【答案】2π 360° π 180°
知识点八 弧度制下的弧长与扇形面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l=αR.
(2)扇形面积公式:S=lR=αR2.
跟踪训练
1.与终边相同的角是( )
A. B. C. D.
【答案】D
【分析】与终边相同的角可表示为.
【详解】∵,
∴与终边相同的角是.
故选:D
2.的角化为弧度制的结果为( )
A. B. C. D.
【答案】C
【分析】根据角度和弧度的换算公式即可得到答案.
【详解】.
故选:C.
3.下列说法正确的是( )
A.终边相同的角相等 B.相等的角终边相同
C.小于的角是锐角 D.第一象限的角是正角
【答案】B
【分析】根据角的定义判断.
【详解】终边相同的角相差周角的整数倍,A不正确;相等的角终边一定相同;所以B正确;小于的角是锐角可以是负角,C错;第一象限的角是正角,也可以是负角,D错误.
故选:B.
4.如图所示的时钟显示的时刻为:,此时时针与分针的夹角为则( )
A. B. C. D.
【答案】B
【分析】由图可知为周角的,计算可得结果.
【详解】解:由图可知,.
故选:B.
5.沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以O为圆心,为半径的圆弧,C是的中点,D在上,.“会圆术”给出后的弧长的近似值s的计算公式:,记实际弧长为l.当,时,的值约为( )(参考数据:,)
A.0.01 B.0.05 C.0.13 D.0.53
【答案】D
【分析】根据题意求出与的值,代入弧长公式和求出和即可.
【详解】因为,所以,
因为是的中点,在上,,
所以延长可得在上,,
所以,
,
所以.
故选:D
6.把表示成,的形式,则的值可以是( )
A. B. C. D.
【答案】B
【分析】由结合弧度制求解即可.
【详解】∵,∴
故选:B
7.角所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【分析】根据角的终边位置可直接得到结果.
【详解】,角位于第三象限.
故选:C.
8.已知一扇形的周长为,则当该扇形的面积取得最大时,圆心角大小为( )
A. B. C.1 D.2
【答案】D
【分析】根据周长建立弧长与半径间的关系,由扇形面积公式可得,利用二次函数求最值,并求出S最大时对应的圆心角即可.
【详解】设扇形的半径为,弧长为,则,
所以,
扇形面积,
当时,有最大值,此时圆心角,
故选:D
二、多选题
9.若是第二象限角,则( )
A.是第一象限角 B.是第一或第三象限角
C.是第二象限角 D.是第三或第四象限角
【答案】AB
【分析】由与关于轴对称,即可判断AD;由已知可得,,再根据不等式的性质可判断B;由是第一象限角判断C.
【详解】解:因为与关于轴对称,而是第二象限角,所以是第三象限角,
所以是第一象限角,故A正确,D错误;
因为是第二象限角,所以,,所以,,
故是第一或第三象限角,故 B正确;
因为是第二象限角,所以是第一象限角,故C错误.
故选:AB.
10.设扇形的圆心角为,半径为,弧长为,面积为,周长为,则( )
A.若,确定,则,唯一确定 B.若,确定,则,唯一确定
C.若,确定,则,唯一确定 D.若,确定,则,唯一确定
【答案】ABD
【分析】由弧长公式和面积公式判断.
【详解】由弧长公式得,,周长,
若,确定,则唯一确定,则,唯一确定,故A正确,
若,确定,则唯一确定,则,唯一确定,故B正确,
若,确定,则,,即,当,有两正实根,不唯一确定,所以,不一定唯一确定,故C错误,
若,确定,则唯一确定,则唯一确定,故D正确,
故选:ABD.
11.下列结论中正确的是( )
A.终边经过点的角的集合是;
B.将表的分针拨慢10分钟,则分针转过的角的弧度数是;
C.若是第三象限角,则是第二象限角,为第一或第二象限角;
D.,,则
【答案】ABD
【分析】直接以角的表示方法,象限角的概念,集合间的关系求出结果.
【详解】A.终边经过点的角的终边在第一象限平分线上,故角的集合是,所以A正确;
B. 将表的分针拨慢10分钟,按逆时针旋转,则分针转过的角度为,对应弧度数是,所以B正确;
C.因为是第三象限角,即,所以,当为奇数时,是第四象限角,当为偶数时,是第二象限角;,所以的终边位置在第一或第二象限或轴非负半轴,所以C错误;
D. ,
,易知,所以D正确;
故选:ABD.
12.已知{第一象限角},{锐角},{小于的角},那么A、B、C关系是( )
A. B. C. D.
【答案】BC
【解析】根据集合中角的范围,对选项逐一分析,由此得出正确选项.
【详解】对于A选项,除了锐角,还包括其它角,比如,所以A选项错误.
对于B选项,锐角是小于的角,故B选项正确.
对于C选项,锐角是第一象限角,故C选项正确.
对于D选项,中角的范围不一样,所以D选项错误.
故选:BC
【点睛】本小题主要考查角的范围比较,考查集合交集、并集和集合相等的概念,属于基础题.
三、填空题
13.写出两个与终边相同的角______.
【答案】,(答案不唯一)
【分析】利用终边相同的角的定义求解.
【详解】设是与终边相同的角,
则,
令,得,
令,得,
故答案为:,(其他正确答案也可)14.半径为2cm,中心角为的扇形的弧长为______cm.
【答案】
【分析】先将圆心角角度化成弧度制,然后直接利用弧长公式进行求解即可.
【详解】解:圆弧所对的中心角为即为弧度,半径为
弧长为.
故答案为:.
15.如图,扇环ABCD中,弧,弧,,则扇环ABCD的面积__________.
【答案】3
【分析】根据弧长公式求出,,再由根据扇形的面积公式求解即可.
【详解】设,
因为弧,弧,,
所以,,
所以,,
又扇形的面积为,扇形的面积为,
所以扇环ABCD的面积.
故答案为:3
16.如图所示,一竖立在地面上的圆锥形物体的母线长为,一只小虫从圆锥的底面圆上的点出发,绕圆锥爬行一周后回到点处,若该小虫爬行的最短路程为,则这个圆锥的体积为___________.
【答案】
【分析】作出该圆锥的侧面展开图,该小虫爬行的最短路程为PP′,由余弦定理求出,求出底面圆的半径r,从而求出这个圆锥的高,由此能求出这个圆锥的体积.
【详解】作出该圆锥的侧面展开图,如图所示:
该小虫爬行的最短路程为PP′,由余弦定理可得:
∴.
设底面圆的半径为r,则有,解得,
所以这个圆锥的高为,
则这个圆锥的体积为.
故答案为:.
【点睛】立体几何中的翻折叠(展开)问题要注意翻折(展开)过程中的不变量.
四、解答题
17.已知.
(1)把表示成的形式,其中,;
(2)求,使与的终边相同,且.
【答案】(1)
(2)
【分析】(1)将直接表示为的形式,其中,;
(2)设,由可求得的值,即可得解.
【解析】(1)解:.
(2)解:,设,
由可得,解得,
,则,故.
18.已知一扇形的圆心角为,半径为,弧长为.
(1)已知扇形的周长为,面积是,求扇形的圆心角;
(2)若扇形周长为,当扇形的圆心角为多少弧度时,这个扇形的面积最大?并求此扇形的最大面积.
【答案】(1)
(2)取得最大值25,此时
【分析】(1)根据弧长公式及扇形的面积公式,再结合扇形的周长公式即可求解;
(2)根据扇形的周长公式及扇形的面积公式,再结合二次函数的性质即可求解.
【解析】(1)由题意得,解得(舍去),.
所以扇形圆心角.
(2)由已知得,.
所以,
所以当时,取得最大值25,
,解得.
当扇形的圆心角为多少弧度时,这个扇形的面积最大为25.
19.已知,,,.
(1)将,用弧度制表示出来,并指出它们各自的终边所在的象限;
(2)将,用角度制表示出来,并在内找出与它们终边相同的所有角.
【答案】(1),第二象限;,第一象限
(2),和;,
【分析】(1)直接将角度转化成弧度表示即可;通过周期公式化简,可求出终边对应象限;
(2)将弧度转化成角度即可;通过任意角概念给赋值,求出在内对应角即可.
(1)由题意,根据角度制与弧度制的互化公式,可得
,
.
又由,所以与角的终边相同,所以终边位于第二象限;
,所以与角的终边相同,所以终边位于第一象限;
(2)根据角度制与弧度制的互化公式,可得,.
根据终边相同角的表示,可得与终边相同的角为,,当时,;当时,.
与终边相同的角为,,
当时,.
因此,在内,与终边相同的角是和,与终边相同的角是
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
