2023年高考数学一轮总复习考点探究与题型突破 第27讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用 精品讲义(Word含答案)
文档属性
| 名称 | 2023年高考数学一轮总复习考点探究与题型突破 第27讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用 精品讲义(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 00:00:00 | ||
图片预览




文档简介
第27讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
1.函数y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ) (A>0,ω>0) 振幅 周期 频率 相位 初相
A T= f== ωx+φ φ
2.用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图
用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图时,要找五个关键点,如下表所示:
ωx+φ 0 π 2π
x - - -
y=Asin(ωx+φ) 0 A 0 -A 0
五点法作图的步骤
用“五点法”作函数y=Asin(ωx+φ)的简图,精髄是通过变量代换,设z=ωx+φ,由z取0,,π,,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象,其中相邻两点的横向距离均为.
3.由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法
考点1 函数y=Asin(ωx+φ)的图象及变换
[名师点睛]
作函数y=Asin(ωx+φ)(A>0,ω>0)的图象常用如下两种方法:
(1)五点法作图:用“五点法”作y=Asin(ωx+φ)的简图,主要是通过变量代换,设z=ωx+φ,由z取0,,π,π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;
(2)图象的变换法:由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
[典例]
1.(2022·浙江·高考真题)为了得到函数的图象,只要把函数图象上所有的点( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
2.(2022·安徽·合肥市第八中学模拟预测(文))若函数(其中)图象的一个对称中心为,其相邻一条对称轴方程为,且函数在该对称轴处取得最小值,为了得到的图象,则只要将f(x)的图象( )
A.向右平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向左平移个单位长度
[举一反三]
1.(2022·湖北·荆州中学三模)要得到函数的图象,只需将函数的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
2.(2022·全国·高三专题练习)由函数的图象经过图象变换得到函数的图象,则这个变换过程为( )
A.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
B.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
C.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
D.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
3.(2022·河北唐山·高三期末)为了得到函数的图像,只需把函数的图像( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右移个单位
考点2 由图象求解析式
[名师点睛]
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
(1)求A,b,确定函数的最大值M和最小值m,
则A=,b=.
(2)求ω,确定函数的最小正周期T,则可得ω=.
(3)求φ,常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上);
②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:
“最大值点”(即图象的“峰点”)时ωx+φ =+2kπ(k∈Z);“最小值点”(即图象的“谷点”)时ωx+φ=+2kπ(k∈Z).
[典例]
1.(2022·广东茂名·二模)已知函数 的部分图象如图所示.将函数的图象向左平移 个单位得到 的图象,则( )
A. ) B.
C. D.
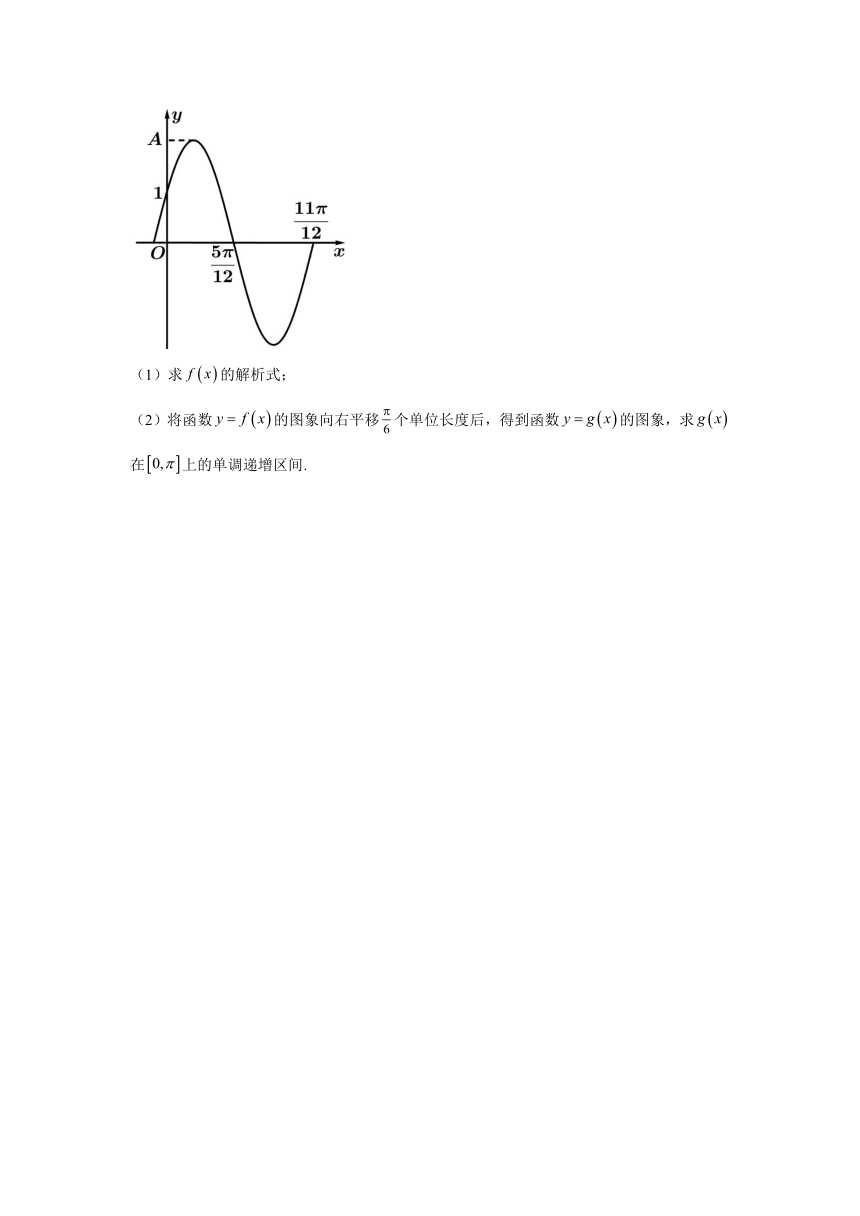
2.(2022·浙江·高三专题练习)已知函数在一个周期内的图象如图所示.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度后,得到函数的图象,求在上的单调递增区间.
[举一反三]
1.(2022·山东潍坊·模拟预测)函数的部分图像如图所示,现将的图像向左平移个单位长度,得到函数的图像,则的表达式可以为( )
A. B.
C. D.
2.(2022·广东惠州·高三阶段练习)已知函数的部分图像如图所示,则将的图像向左平移个单位后,所得图像的函数解析式为( )
A. B.
C. D.
3.(2022·河北·模拟预测)已知函数的图象过点,且相邻两个零点的距离为.若将函数的图象向左平移个单位长度得到的图象,则函数的解析式为___________.
4.(2022·全国·高三专题练习)函数的部分图象如图所示,若将图象上的所有点向左平移个单位得到函数的图象,则函数___________.
考点3 函数y=Asin(ωx+φ)图象与性质的综合应用
[名师点睛]
先将y=f(x)化为y=Asin(ωx+φ)+B的形式,再借助y=Asin(ωx+φ)的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
[典例]
1.(多选)(2022·江苏徐州·模拟预测)已知函数,若函数的部分图象如图所示,则关于函数,下列结论中正确的是( )
A.函数的图象关于直线对称
B.函数的图象关于点对称
C.函数在区间上的减区间为
D.函数的图象可由函数的图象向左平移个单位长度而得到
2.(2022·湖北·襄阳五中模拟预测)已知数的相邻两对称轴间的距离为.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度,再把各点的横坐标缩小为原来的(纵坐标不变),得到函数的图象,当时,求函数的值域;
(3)对于第(2)问中的函数,记方程在上的根从小到大依次为,若,试求与的值.
[举一反三]
1.(2022·天津·高考真题)已知,关于该函数有下面四个说法:
①的最小正周期为;
②在上单调递增;
③当时,的值域为;
④的图象可由的图象向左平移个单位长度得到.
以上四个说法中,正确的个数有( )
A. B. C. D.
2.(2022·江苏南京·高三开学考试)设函数有个不同的零点,则正实数的取值范围为( )
A. B.
C. D.
3.(多选)(2022·湖南·岳阳市教育科学技术研究院三模)若函数的图象向右平移个单位长度后,得到函数的图象,则下列关于函数的说法中,错误的是( )
A.数的图象关于直线对称
B.函数的图象关于点对称
C.函数的单调递增区间为
D.函数是偶函数
4.(2022·重庆八中模拟预测)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象上所有的点向右平移个单位,再将所得图象上每一个点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象.当时,方程恰有三个不相等的实数根,求实数a的取值范围和的值.
考点4 三角函数模型及其应用
[名师点睛]
三角函数模型在实际应用中体现的两个方面
(1)已知函数模型,利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与因变量之间的对应法则;
(2)需要建立精确的或者数据拟合的模型去解决问题,尤其是利用已知数据建立拟合函数解决实际问题,此类问题体现了数学建模核心素养,考查应用意识.
[典例]
1.(2022·北京东城·三模)如图,某摩天轮最高点距离地面高度为,转盘直径为,开启后按逆时针方向匀速旋转,旋转一周需要.游客在座舱转到距离地面最近的位置进舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
2.(2022·上海·华东师范大学附属东昌中学高三阶段练习)降噪耳机主要有主动降噪耳机和被动降噪耳机两种.其中主动降噪耳机的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的反向声波来抵消噪声(如图所示).已知某噪声的声波曲线是,其中的振幅为,且经过点
(1)求该噪声声波曲线的解析式以及降噪芯片生成的降噪声波曲线的解析式;
(2)先将函数图象上各点的横坐标变为原来的倍,纵坐标不变,再将所得函数图象向右平移个单位,得到函数的图象.若锐角满足,求的值.
[举一反三]
1.(2022·天津滨海新·高三阶段练习)筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图1).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.如图2,将筒车抽象为一个半径为的圆,设筒车按逆时针方向每旋转一周用时秒,当时,盛水筒位于点,经过秒后运动到点,点的纵坐标满足(,,),则下列叙述不正确的是( )
A.筒车转动的角速度
B.当筒车旋转秒时,盛水筒对应的点的纵坐标为
C.当筒车旋转秒时,盛水筒和初始点的水平距离为
D.筒车在秒的旋转过程中,盛水筒最高点到轴的距离的最大值为
2.(2022·山东·烟台二中高三期末)武威“天马之眼”摩天轮,于2014年5月建成运营.夜间的“天马之眼”摩天轮美轮美奂,绚丽多彩,气势宏大,震撼人心,是武威一颗耀眼的明珠.该摩天轮直径为120米,摩天轮的最高点距地面128米,摩天轮匀速转动,每转动一圈需要t分钟,若小夏同学从摩天轮的最低点处登上摩天轮,从小夏登上摩天轮的时刻开始计时.
(1)求小夏与地面的距离y(米)与时间x(分钟)的函数关系式;
(2)在摩天轮转动一圈的过程中,小夏的高度在距地面不低于98米的时间不少分钟,求t的最小值
第27讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
1.函数y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ) (A>0,ω>0) 振幅 周期 频率 相位 初相
A T= f== ωx+φ φ
2.用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图
用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图时,要找五个关键点,如下表所示:
ωx+φ 0 π 2π
x - - -
y=Asin(ωx+φ) 0 A 0 -A 0
五点法作图的步骤
用“五点法”作函数y=Asin(ωx+φ)的简图,精髄是通过变量代换,设z=ωx+φ,由z取0,,π,,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象,其中相邻两点的横向距离均为.
3.由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法
考点1 函数y=Asin(ωx+φ)的图象及变换
[名师点睛]
作函数y=Asin(ωx+φ)(A>0,ω>0)的图象常用如下两种方法:
(1)五点法作图:用“五点法”作y=Asin(ωx+φ)的简图,主要是通过变量代换,设z=ωx+φ,由z取0,,π,π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;
(2)图象的变换法:由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
[典例]
1.(2022·浙江·高考真题)为了得到函数的图象,只要把函数图象上所有的点( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
【答案】D
【解析】因为,所以把函数图象上的所有点向右平移个单位长度即可得到函数的图象.
故选:D.
2.(2022·安徽·合肥市第八中学模拟预测(文))若函数(其中)图象的一个对称中心为,其相邻一条对称轴方程为,且函数在该对称轴处取得最小值,为了得到的图象,则只要将f(x)的图象( )
A.向右平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向左平移个单位长度
【答案】D
【解析】解:函数图象的一个对称中心为,其相邻一条对称轴方程为,
所以,
所以.
因为函数在时取得最小值,
所以,,
∴ ,
∵∴
∴
根据平移变换规律可知,向左平移个单位,可得函数,
所以向左平移个单位可得的图象,
故选:D.
[举一反三]
1.(2022·湖北·荆州中学三模)要得到函数的图象,只需将函数的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
【答案】A
【解析】,所以的图象向左平移个单位得:.
故选:A.
2.(2022·全国·高三专题练习)由函数的图象经过图象变换得到函数的图象,则这个变换过程为( )
A.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
B.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
C.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
D.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
【答案】A
【解析】的图象经过图象变换得到函数的图象,
可先平移后伸缩:
将函数图象向左平移个单位长度得,再将所有点的横坐标扩大为原来的2倍(纵坐标不变),即可得到的图象;
先伸缩后平移:
把所有点的横坐标伸长为原来的2倍(纵坐标不变),得到,再将图象左移个单位,得到的图象.
故选:A
3.(2022·河北唐山·高三期末)为了得到函数的图像,只需把函数的图像( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右移个单位
【答案】D
【解析】因为:.
所以:函数的图象向右平移个单位,
可得到函数的图象.
故选:D.
考点2 由图象求解析式
[名师点睛]
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
(1)求A,b,确定函数的最大值M和最小值m,
则A=,b=.
(2)求ω,确定函数的最小正周期T,则可得ω=.
(3)求φ,常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上);
②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:
“最大值点”(即图象的“峰点”)时ωx+φ =+2kπ(k∈Z);“最小值点”(即图象的“谷点”)时ωx+φ=+2kπ(k∈Z).
[典例]
1.(2022·广东茂名·二模)已知函数 的部分图象如图所示.将函数的图象向左平移 个单位得到 的图象,则( )
A. ) B.
C. D.
【答案】D
【解析】由图象知,,
∵,
∴,
又,∴,
∴,
∵将函数的图象向左平移个单位得到的图象,
∴,
故选:D.
2.(2022·浙江·高三专题练习)已知函数在一个周期内的图象如图所示.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度后,得到函数的图象,求在上的单调递增区间.
【解】(1)由图可得函数的最小正周期为,
所以,,
,则,
,则,,则,所以,,
因为,所以,,所以,;
(2)由题意可得,
令,,得,,
记,则.
因此,函数在上的增区间是、.
[举一反三]
1.(2022·山东潍坊·模拟预测)函数的部分图像如图所示,现将的图像向左平移个单位长度,得到函数的图像,则的表达式可以为( )
A. B.
C. D.
【答案】B
【解析】由图像可知:,;
又,,又,,
,由五点作图法可知:,解得:,;
.
故选:B.
2.(2022·广东惠州·高三阶段练习)已知函数的部分图像如图所示,则将的图像向左平移个单位后,所得图像的函数解析式为( )
A. B.
C. D.
【答案】B
【解析】由题,
由图,,
所以,向左平移个单位后,
得到
故选:B.
3.(2022·河北·模拟预测)已知函数的图象过点,且相邻两个零点的距离为.若将函数的图象向左平移个单位长度得到的图象,则函数的解析式为___________.
【答案】
【解析】的相邻两个零点的距离为,的最小正周期,;
又,,解得:,
又,,,
.
故答案为:.
4.(2022·全国·高三专题练习)函数的部分图象如图所示,若将图象上的所有点向左平移个单位得到函数的图象,则函数___________.
【答案】
【解析】根据函数的部分图象,
可得,,.
再结合五点法作图,可得,,.
将图象上的所有点向左平移个单位得到函数的图象,
故答案为:.
考点3 函数y=Asin(ωx+φ)图象与性质的综合应用
[名师点睛]
先将y=f(x)化为y=Asin(ωx+φ)+B的形式,再借助y=Asin(ωx+φ)的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
[典例]
1.(多选)(2022·江苏徐州·模拟预测)已知函数,若函数的部分图象如图所示,则关于函数,下列结论中正确的是( )
A.函数的图象关于直线对称
B.函数的图象关于点对称
C.函数在区间上的减区间为
D.函数的图象可由函数的图象向左平移个单位长度而得到
【答案】BC
【解析】根据函数图象可得:,∴,,
又,故,
所以对称轴为时,故A项错.
,∴关于对称,故B项对.
函数的单调递减区间为,
时在单调递减,故C项对.
,故D项错.
故选:BC.
2.(2022·湖北·襄阳五中模拟预测)已知数的相邻两对称轴间的距离为.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度,再把各点的横坐标缩小为原来的(纵坐标不变),得到函数的图象,当时,求函数的值域;
(3)对于第(2)问中的函数,记方程在上的根从小到大依次为,若,试求与的值.
【解析】(1)由题意,函数
因为函数图象的相邻两对称轴间的距离为,所以,可得.
故
(2)将函数的图象向右平移个单位长度,可得的图象.
再把橫坐标缩小为原来的,得到函数的图象.
当时,,
当时,函数取得最小值,最小值为,
当时,函数取得最大值,最大值为,
故函数的值域.
(3)由方程,即,即,
因为,可得,
设,其中,即,结合正弦函数的图象,
可得方程在区间有5个解,即,
其中,
即
解得
所以.
综上,
[举一反三]
1.(2022·天津·高考真题)已知,关于该函数有下面四个说法:
①的最小正周期为;
②在上单调递增;
③当时,的值域为;
④的图象可由的图象向左平移个单位长度得到.
以上四个说法中,正确的个数有( )
A. B. C. D.
【答案】A
【解析】因为,所以的最小正周期为,①不正确;
令,而在上递增,所以在上单调递增,②正确;因为,,所以,③不正确;
由于,所以的图象可由的图象向右平移个单位长度得到,④不正确.
故选:A.
2.(2022·江苏南京·高三开学考试)设函数有个不同的零点,则正实数的取值范围为( )
A. B.
C. D.
【答案】A
【解析】由题,当时,,显然单调递增,且,,所有此时有且只有一个零点,
所有当时,有4个零点,令,即,解得,
由题可得区间内的4个零点分别是,所以即在之间,
即,解得
故选:A
3.(多选)(2022·湖南·岳阳市教育科学技术研究院三模)若函数的图象向右平移个单位长度后,得到函数的图象,则下列关于函数的说法中,错误的是( )
A.数的图象关于直线对称
B.函数的图象关于点对称
C.函数的单调递增区间为
D.函数是偶函数
【答案】ABC
【解析】由题意得:,
将代入得:
故A错误;
将代入得:,B错误;
令,解得:,
故)的单调递增区间不是,C错误;
,为偶函数,D选项正确.
故选:ABC
4.(2022·重庆八中模拟预测)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象上所有的点向右平移个单位,再将所得图象上每一个点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象.当时,方程恰有三个不相等的实数根,求实数a的取值范围和的值.
【解】(1)解:由图示得:,
又,所以,所以,所以,
又因为过点,所以,即,
所以,解得,又,所以,
所以;
(2)解:由已知得,
当时,,令,则,
令,则
,,,,
所以,
因为有三个不同的实数根,则,
所以,即,
所以.
考点4 三角函数模型及其应用
[名师点睛]
三角函数模型在实际应用中体现的两个方面
(1)已知函数模型,利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与因变量之间的对应法则;
(2)需要建立精确的或者数据拟合的模型去解决问题,尤其是利用已知数据建立拟合函数解决实际问题,此类问题体现了数学建模核心素养,考查应用意识.
[典例]
1.(2022·北京东城·三模)如图,某摩天轮最高点距离地面高度为,转盘直径为,开启后按逆时针方向匀速旋转,旋转一周需要.游客在座舱转到距离地面最近的位置进舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
【答案】B
【解析】解:根据题意设,,
因为某摩天轮最高点距离地面高度为,转盘直径为,
所以,该摩天轮最低点距离地面高度为,
所以,解得,
因为开启后按逆时针方向匀速旋转,旋转一周需要,
所以,,解得,
因为时,,故,即,解得.
所以,
故选:B
2.(2022·上海·华东师范大学附属东昌中学高三阶段练习)降噪耳机主要有主动降噪耳机和被动降噪耳机两种.其中主动降噪耳机的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的反向声波来抵消噪声(如图所示).已知某噪声的声波曲线是,其中的振幅为,且经过点
(1)求该噪声声波曲线的解析式以及降噪芯片生成的降噪声波曲线的解析式;
(2)先将函数图象上各点的横坐标变为原来的倍,纵坐标不变,再将所得函数图象向右平移个单位,得到函数的图象.若锐角满足,求的值.
【解】(1)解:由已知可得,,可得,
所以,,得,
因为,则,故,
.
(2)解;将函数图象上各点的横坐标变为原来的倍,纵坐标不变,可得到函数的图象,再将所得函数图象向右平移个单位,可得函数的图象,则,
因为,则,
,则,故.
[举一反三]
1.(2022·天津滨海新·高三阶段练习)筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图1).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.如图2,将筒车抽象为一个半径为的圆,设筒车按逆时针方向每旋转一周用时秒,当时,盛水筒位于点,经过秒后运动到点,点的纵坐标满足(,,),则下列叙述不正确的是( )
A.筒车转动的角速度
B.当筒车旋转秒时,盛水筒对应的点的纵坐标为
C.当筒车旋转秒时,盛水筒和初始点的水平距离为
D.筒车在秒的旋转过程中,盛水筒最高点到轴的距离的最大值为
【答案】B
【解析】A:因为筒车按逆时针方向每旋转一周用时秒,
所以,因此本选项叙述正确;
B:因为当时,盛水筒位于点,所以,
所以有,因为,所以,
即,
所以,
因此本选项叙述不正确;
C:由B可知:盛水筒的纵坐标为,设它的横坐标为,
所以有,因为筒车旋转秒时,所以此时盛水筒在第三象限,故,盛水筒和初始点的水平距离为,因此本选项叙述正确;
D:因为,所以筒车在秒的旋转过程中,盛水筒最高点到轴的距离的最大值为,因此本选项叙述正确,
故选:B
2.(2022·山东·烟台二中高三期末)武威“天马之眼”摩天轮,于2014年5月建成运营.夜间的“天马之眼”摩天轮美轮美奂,绚丽多彩,气势宏大,震撼人心,是武威一颗耀眼的明珠.该摩天轮直径为120米,摩天轮的最高点距地面128米,摩天轮匀速转动,每转动一圈需要t分钟,若小夏同学从摩天轮的最低点处登上摩天轮,从小夏登上摩天轮的时刻开始计时.
(1)求小夏与地面的距离y(米)与时间x(分钟)的函数关系式;
(2)在摩天轮转动一圈的过程中,小夏的高度在距地面不低于98米的时间不少分钟,求t的最小值.
【解】(1)如图,以摩天轮最低点的正下方的地面处为原点,
以地平面所在直线为x轴建立平面直角坐标系,
摩天轮的最高点距地面128米,摩天轮的半径为60米,摩天轮的圆心O到地面的距离为68米.
因为每转动一圈需要t分钟,所以.
.
(2)依题意,可知,即,
不妨取第一圈,可得,,
持续时间为,即,故t的最小值为25
1.函数y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ) (A>0,ω>0) 振幅 周期 频率 相位 初相
A T= f== ωx+φ φ
2.用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图
用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图时,要找五个关键点,如下表所示:
ωx+φ 0 π 2π
x - - -
y=Asin(ωx+φ) 0 A 0 -A 0
五点法作图的步骤
用“五点法”作函数y=Asin(ωx+φ)的简图,精髄是通过变量代换,设z=ωx+φ,由z取0,,π,,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象,其中相邻两点的横向距离均为.
3.由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法
考点1 函数y=Asin(ωx+φ)的图象及变换
[名师点睛]
作函数y=Asin(ωx+φ)(A>0,ω>0)的图象常用如下两种方法:
(1)五点法作图:用“五点法”作y=Asin(ωx+φ)的简图,主要是通过变量代换,设z=ωx+φ,由z取0,,π,π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;
(2)图象的变换法:由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
[典例]
1.(2022·浙江·高考真题)为了得到函数的图象,只要把函数图象上所有的点( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
2.(2022·安徽·合肥市第八中学模拟预测(文))若函数(其中)图象的一个对称中心为,其相邻一条对称轴方程为,且函数在该对称轴处取得最小值,为了得到的图象,则只要将f(x)的图象( )
A.向右平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向左平移个单位长度
[举一反三]
1.(2022·湖北·荆州中学三模)要得到函数的图象,只需将函数的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
2.(2022·全国·高三专题练习)由函数的图象经过图象变换得到函数的图象,则这个变换过程为( )
A.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
B.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
C.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
D.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
3.(2022·河北唐山·高三期末)为了得到函数的图像,只需把函数的图像( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右移个单位
考点2 由图象求解析式
[名师点睛]
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
(1)求A,b,确定函数的最大值M和最小值m,
则A=,b=.
(2)求ω,确定函数的最小正周期T,则可得ω=.
(3)求φ,常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上);
②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:
“最大值点”(即图象的“峰点”)时ωx+φ =+2kπ(k∈Z);“最小值点”(即图象的“谷点”)时ωx+φ=+2kπ(k∈Z).
[典例]
1.(2022·广东茂名·二模)已知函数 的部分图象如图所示.将函数的图象向左平移 个单位得到 的图象,则( )
A. ) B.
C. D.
2.(2022·浙江·高三专题练习)已知函数在一个周期内的图象如图所示.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度后,得到函数的图象,求在上的单调递增区间.
[举一反三]
1.(2022·山东潍坊·模拟预测)函数的部分图像如图所示,现将的图像向左平移个单位长度,得到函数的图像,则的表达式可以为( )
A. B.
C. D.
2.(2022·广东惠州·高三阶段练习)已知函数的部分图像如图所示,则将的图像向左平移个单位后,所得图像的函数解析式为( )
A. B.
C. D.
3.(2022·河北·模拟预测)已知函数的图象过点,且相邻两个零点的距离为.若将函数的图象向左平移个单位长度得到的图象,则函数的解析式为___________.
4.(2022·全国·高三专题练习)函数的部分图象如图所示,若将图象上的所有点向左平移个单位得到函数的图象,则函数___________.
考点3 函数y=Asin(ωx+φ)图象与性质的综合应用
[名师点睛]
先将y=f(x)化为y=Asin(ωx+φ)+B的形式,再借助y=Asin(ωx+φ)的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
[典例]
1.(多选)(2022·江苏徐州·模拟预测)已知函数,若函数的部分图象如图所示,则关于函数,下列结论中正确的是( )
A.函数的图象关于直线对称
B.函数的图象关于点对称
C.函数在区间上的减区间为
D.函数的图象可由函数的图象向左平移个单位长度而得到
2.(2022·湖北·襄阳五中模拟预测)已知数的相邻两对称轴间的距离为.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度,再把各点的横坐标缩小为原来的(纵坐标不变),得到函数的图象,当时,求函数的值域;
(3)对于第(2)问中的函数,记方程在上的根从小到大依次为,若,试求与的值.
[举一反三]
1.(2022·天津·高考真题)已知,关于该函数有下面四个说法:
①的最小正周期为;
②在上单调递增;
③当时,的值域为;
④的图象可由的图象向左平移个单位长度得到.
以上四个说法中,正确的个数有( )
A. B. C. D.
2.(2022·江苏南京·高三开学考试)设函数有个不同的零点,则正实数的取值范围为( )
A. B.
C. D.
3.(多选)(2022·湖南·岳阳市教育科学技术研究院三模)若函数的图象向右平移个单位长度后,得到函数的图象,则下列关于函数的说法中,错误的是( )
A.数的图象关于直线对称
B.函数的图象关于点对称
C.函数的单调递增区间为
D.函数是偶函数
4.(2022·重庆八中模拟预测)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象上所有的点向右平移个单位,再将所得图象上每一个点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象.当时,方程恰有三个不相等的实数根,求实数a的取值范围和的值.
考点4 三角函数模型及其应用
[名师点睛]
三角函数模型在实际应用中体现的两个方面
(1)已知函数模型,利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与因变量之间的对应法则;
(2)需要建立精确的或者数据拟合的模型去解决问题,尤其是利用已知数据建立拟合函数解决实际问题,此类问题体现了数学建模核心素养,考查应用意识.
[典例]
1.(2022·北京东城·三模)如图,某摩天轮最高点距离地面高度为,转盘直径为,开启后按逆时针方向匀速旋转,旋转一周需要.游客在座舱转到距离地面最近的位置进舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
2.(2022·上海·华东师范大学附属东昌中学高三阶段练习)降噪耳机主要有主动降噪耳机和被动降噪耳机两种.其中主动降噪耳机的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的反向声波来抵消噪声(如图所示).已知某噪声的声波曲线是,其中的振幅为,且经过点
(1)求该噪声声波曲线的解析式以及降噪芯片生成的降噪声波曲线的解析式;
(2)先将函数图象上各点的横坐标变为原来的倍,纵坐标不变,再将所得函数图象向右平移个单位,得到函数的图象.若锐角满足,求的值.
[举一反三]
1.(2022·天津滨海新·高三阶段练习)筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图1).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.如图2,将筒车抽象为一个半径为的圆,设筒车按逆时针方向每旋转一周用时秒,当时,盛水筒位于点,经过秒后运动到点,点的纵坐标满足(,,),则下列叙述不正确的是( )
A.筒车转动的角速度
B.当筒车旋转秒时,盛水筒对应的点的纵坐标为
C.当筒车旋转秒时,盛水筒和初始点的水平距离为
D.筒车在秒的旋转过程中,盛水筒最高点到轴的距离的最大值为
2.(2022·山东·烟台二中高三期末)武威“天马之眼”摩天轮,于2014年5月建成运营.夜间的“天马之眼”摩天轮美轮美奂,绚丽多彩,气势宏大,震撼人心,是武威一颗耀眼的明珠.该摩天轮直径为120米,摩天轮的最高点距地面128米,摩天轮匀速转动,每转动一圈需要t分钟,若小夏同学从摩天轮的最低点处登上摩天轮,从小夏登上摩天轮的时刻开始计时.
(1)求小夏与地面的距离y(米)与时间x(分钟)的函数关系式;
(2)在摩天轮转动一圈的过程中,小夏的高度在距地面不低于98米的时间不少分钟,求t的最小值
第27讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
1.函数y=Asin(ωx+φ)的有关概念
y=Asin(ωx+φ) (A>0,ω>0) 振幅 周期 频率 相位 初相
A T= f== ωx+φ φ
2.用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图
用五点法画y=Asin(ωx+φ)(A>0,ω>0)一个周期内的简图时,要找五个关键点,如下表所示:
ωx+φ 0 π 2π
x - - -
y=Asin(ωx+φ) 0 A 0 -A 0
五点法作图的步骤
用“五点法”作函数y=Asin(ωx+φ)的简图,精髄是通过变量代换,设z=ωx+φ,由z取0,,π,,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象,其中相邻两点的横向距离均为.
3.由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象的两种方法
考点1 函数y=Asin(ωx+φ)的图象及变换
[名师点睛]
作函数y=Asin(ωx+φ)(A>0,ω>0)的图象常用如下两种方法:
(1)五点法作图:用“五点法”作y=Asin(ωx+φ)的简图,主要是通过变量代换,设z=ωx+φ,由z取0,,π,π,2π来求出相应的x,通过列表,计算得出五点坐标,描点后得出图象;
(2)图象的变换法:由函数y=sin x的图象通过变换得到y=Asin(ωx+φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.
[典例]
1.(2022·浙江·高考真题)为了得到函数的图象,只要把函数图象上所有的点( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
【答案】D
【解析】因为,所以把函数图象上的所有点向右平移个单位长度即可得到函数的图象.
故选:D.
2.(2022·安徽·合肥市第八中学模拟预测(文))若函数(其中)图象的一个对称中心为,其相邻一条对称轴方程为,且函数在该对称轴处取得最小值,为了得到的图象,则只要将f(x)的图象( )
A.向右平移个单位长度 B.向左平移个单位长度
C.向右平移个单位长度 D.向左平移个单位长度
【答案】D
【解析】解:函数图象的一个对称中心为,其相邻一条对称轴方程为,
所以,
所以.
因为函数在时取得最小值,
所以,,
∴ ,
∵∴
∴
根据平移变换规律可知,向左平移个单位,可得函数,
所以向左平移个单位可得的图象,
故选:D.
[举一反三]
1.(2022·湖北·荆州中学三模)要得到函数的图象,只需将函数的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
【答案】A
【解析】,所以的图象向左平移个单位得:.
故选:A.
2.(2022·全国·高三专题练习)由函数的图象经过图象变换得到函数的图象,则这个变换过程为( )
A.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
B.向左平移个单位长度,把所有点的横坐标扩大为原来的2倍(纵坐标不变)
C.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
D.把所有点的横坐标缩小为原来的(纵坐标不变),向左平移个单位长度
【答案】A
【解析】的图象经过图象变换得到函数的图象,
可先平移后伸缩:
将函数图象向左平移个单位长度得,再将所有点的横坐标扩大为原来的2倍(纵坐标不变),即可得到的图象;
先伸缩后平移:
把所有点的横坐标伸长为原来的2倍(纵坐标不变),得到,再将图象左移个单位,得到的图象.
故选:A
3.(2022·河北唐山·高三期末)为了得到函数的图像,只需把函数的图像( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右移个单位
【答案】D
【解析】因为:.
所以:函数的图象向右平移个单位,
可得到函数的图象.
故选:D.
考点2 由图象求解析式
[名师点睛]
确定y=Asin(ωx+φ)+b(A>0,ω>0)的步骤和方法
(1)求A,b,确定函数的最大值M和最小值m,
则A=,b=.
(2)求ω,确定函数的最小正周期T,则可得ω=.
(3)求φ,常用的方法有:
①代入法:把图象上的一个已知点代入(此时A,ω,b已知)或代入图象与直线y=b的交点求解(此时要注意交点在上升区间上还是在下降区间上);
②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:
“最大值点”(即图象的“峰点”)时ωx+φ =+2kπ(k∈Z);“最小值点”(即图象的“谷点”)时ωx+φ=+2kπ(k∈Z).
[典例]
1.(2022·广东茂名·二模)已知函数 的部分图象如图所示.将函数的图象向左平移 个单位得到 的图象,则( )
A. ) B.
C. D.
【答案】D
【解析】由图象知,,
∵,
∴,
又,∴,
∴,
∵将函数的图象向左平移个单位得到的图象,
∴,
故选:D.
2.(2022·浙江·高三专题练习)已知函数在一个周期内的图象如图所示.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度后,得到函数的图象,求在上的单调递增区间.
【解】(1)由图可得函数的最小正周期为,
所以,,
,则,
,则,,则,所以,,
因为,所以,,所以,;
(2)由题意可得,
令,,得,,
记,则.
因此,函数在上的增区间是、.
[举一反三]
1.(2022·山东潍坊·模拟预测)函数的部分图像如图所示,现将的图像向左平移个单位长度,得到函数的图像,则的表达式可以为( )
A. B.
C. D.
【答案】B
【解析】由图像可知:,;
又,,又,,
,由五点作图法可知:,解得:,;
.
故选:B.
2.(2022·广东惠州·高三阶段练习)已知函数的部分图像如图所示,则将的图像向左平移个单位后,所得图像的函数解析式为( )
A. B.
C. D.
【答案】B
【解析】由题,
由图,,
所以,向左平移个单位后,
得到
故选:B.
3.(2022·河北·模拟预测)已知函数的图象过点,且相邻两个零点的距离为.若将函数的图象向左平移个单位长度得到的图象,则函数的解析式为___________.
【答案】
【解析】的相邻两个零点的距离为,的最小正周期,;
又,,解得:,
又,,,
.
故答案为:.
4.(2022·全国·高三专题练习)函数的部分图象如图所示,若将图象上的所有点向左平移个单位得到函数的图象,则函数___________.
【答案】
【解析】根据函数的部分图象,
可得,,.
再结合五点法作图,可得,,.
将图象上的所有点向左平移个单位得到函数的图象,
故答案为:.
考点3 函数y=Asin(ωx+φ)图象与性质的综合应用
[名师点睛]
先将y=f(x)化为y=Asin(ωx+φ)+B的形式,再借助y=Asin(ωx+φ)的图象和性质(如定义域、值域、最值、周期性、对称性、单调性等)解决相关问题.
[典例]
1.(多选)(2022·江苏徐州·模拟预测)已知函数,若函数的部分图象如图所示,则关于函数,下列结论中正确的是( )
A.函数的图象关于直线对称
B.函数的图象关于点对称
C.函数在区间上的减区间为
D.函数的图象可由函数的图象向左平移个单位长度而得到
【答案】BC
【解析】根据函数图象可得:,∴,,
又,故,
所以对称轴为时,故A项错.
,∴关于对称,故B项对.
函数的单调递减区间为,
时在单调递减,故C项对.
,故D项错.
故选:BC.
2.(2022·湖北·襄阳五中模拟预测)已知数的相邻两对称轴间的距离为.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度,再把各点的横坐标缩小为原来的(纵坐标不变),得到函数的图象,当时,求函数的值域;
(3)对于第(2)问中的函数,记方程在上的根从小到大依次为,若,试求与的值.
【解析】(1)由题意,函数
因为函数图象的相邻两对称轴间的距离为,所以,可得.
故
(2)将函数的图象向右平移个单位长度,可得的图象.
再把橫坐标缩小为原来的,得到函数的图象.
当时,,
当时,函数取得最小值,最小值为,
当时,函数取得最大值,最大值为,
故函数的值域.
(3)由方程,即,即,
因为,可得,
设,其中,即,结合正弦函数的图象,
可得方程在区间有5个解,即,
其中,
即
解得
所以.
综上,
[举一反三]
1.(2022·天津·高考真题)已知,关于该函数有下面四个说法:
①的最小正周期为;
②在上单调递增;
③当时,的值域为;
④的图象可由的图象向左平移个单位长度得到.
以上四个说法中,正确的个数有( )
A. B. C. D.
【答案】A
【解析】因为,所以的最小正周期为,①不正确;
令,而在上递增,所以在上单调递增,②正确;因为,,所以,③不正确;
由于,所以的图象可由的图象向右平移个单位长度得到,④不正确.
故选:A.
2.(2022·江苏南京·高三开学考试)设函数有个不同的零点,则正实数的取值范围为( )
A. B.
C. D.
【答案】A
【解析】由题,当时,,显然单调递增,且,,所有此时有且只有一个零点,
所有当时,有4个零点,令,即,解得,
由题可得区间内的4个零点分别是,所以即在之间,
即,解得
故选:A
3.(多选)(2022·湖南·岳阳市教育科学技术研究院三模)若函数的图象向右平移个单位长度后,得到函数的图象,则下列关于函数的说法中,错误的是( )
A.数的图象关于直线对称
B.函数的图象关于点对称
C.函数的单调递增区间为
D.函数是偶函数
【答案】ABC
【解析】由题意得:,
将代入得:
故A错误;
将代入得:,B错误;
令,解得:,
故)的单调递增区间不是,C错误;
,为偶函数,D选项正确.
故选:ABC
4.(2022·重庆八中模拟预测)已知函数的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象上所有的点向右平移个单位,再将所得图象上每一个点的横坐标变为原来的2倍(纵坐标不变),得到函数的图象.当时,方程恰有三个不相等的实数根,求实数a的取值范围和的值.
【解】(1)解:由图示得:,
又,所以,所以,所以,
又因为过点,所以,即,
所以,解得,又,所以,
所以;
(2)解:由已知得,
当时,,令,则,
令,则
,,,,
所以,
因为有三个不同的实数根,则,
所以,即,
所以.
考点4 三角函数模型及其应用
[名师点睛]
三角函数模型在实际应用中体现的两个方面
(1)已知函数模型,利用三角函数的有关性质解决问题,其关键是准确理解自变量的意义及自变量与因变量之间的对应法则;
(2)需要建立精确的或者数据拟合的模型去解决问题,尤其是利用已知数据建立拟合函数解决实际问题,此类问题体现了数学建模核心素养,考查应用意识.
[典例]
1.(2022·北京东城·三模)如图,某摩天轮最高点距离地面高度为,转盘直径为,开启后按逆时针方向匀速旋转,旋转一周需要.游客在座舱转到距离地面最近的位置进舱,开始转动后距离地面的高度为,则在转动一周的过程中,高度关于时间的函数解析式是( )
A.
B.
C.
D.
【答案】B
【解析】解:根据题意设,,
因为某摩天轮最高点距离地面高度为,转盘直径为,
所以,该摩天轮最低点距离地面高度为,
所以,解得,
因为开启后按逆时针方向匀速旋转,旋转一周需要,
所以,,解得,
因为时,,故,即,解得.
所以,
故选:B
2.(2022·上海·华东师范大学附属东昌中学高三阶段练习)降噪耳机主要有主动降噪耳机和被动降噪耳机两种.其中主动降噪耳机的工作原理是:先通过微型麦克风采集周围的噪声,然后降噪芯片生成与噪声振幅相同、相位相反的反向声波来抵消噪声(如图所示).已知某噪声的声波曲线是,其中的振幅为,且经过点
(1)求该噪声声波曲线的解析式以及降噪芯片生成的降噪声波曲线的解析式;
(2)先将函数图象上各点的横坐标变为原来的倍,纵坐标不变,再将所得函数图象向右平移个单位,得到函数的图象.若锐角满足,求的值.
【解】(1)解:由已知可得,,可得,
所以,,得,
因为,则,故,
.
(2)解;将函数图象上各点的横坐标变为原来的倍,纵坐标不变,可得到函数的图象,再将所得函数图象向右平移个单位,可得函数的图象,则,
因为,则,
,则,故.
[举一反三]
1.(2022·天津滨海新·高三阶段练习)筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图1).假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.如图2,将筒车抽象为一个半径为的圆,设筒车按逆时针方向每旋转一周用时秒,当时,盛水筒位于点,经过秒后运动到点,点的纵坐标满足(,,),则下列叙述不正确的是( )
A.筒车转动的角速度
B.当筒车旋转秒时,盛水筒对应的点的纵坐标为
C.当筒车旋转秒时,盛水筒和初始点的水平距离为
D.筒车在秒的旋转过程中,盛水筒最高点到轴的距离的最大值为
【答案】B
【解析】A:因为筒车按逆时针方向每旋转一周用时秒,
所以,因此本选项叙述正确;
B:因为当时,盛水筒位于点,所以,
所以有,因为,所以,
即,
所以,
因此本选项叙述不正确;
C:由B可知:盛水筒的纵坐标为,设它的横坐标为,
所以有,因为筒车旋转秒时,所以此时盛水筒在第三象限,故,盛水筒和初始点的水平距离为,因此本选项叙述正确;
D:因为,所以筒车在秒的旋转过程中,盛水筒最高点到轴的距离的最大值为,因此本选项叙述正确,
故选:B
2.(2022·山东·烟台二中高三期末)武威“天马之眼”摩天轮,于2014年5月建成运营.夜间的“天马之眼”摩天轮美轮美奂,绚丽多彩,气势宏大,震撼人心,是武威一颗耀眼的明珠.该摩天轮直径为120米,摩天轮的最高点距地面128米,摩天轮匀速转动,每转动一圈需要t分钟,若小夏同学从摩天轮的最低点处登上摩天轮,从小夏登上摩天轮的时刻开始计时.
(1)求小夏与地面的距离y(米)与时间x(分钟)的函数关系式;
(2)在摩天轮转动一圈的过程中,小夏的高度在距地面不低于98米的时间不少分钟,求t的最小值.
【解】(1)如图,以摩天轮最低点的正下方的地面处为原点,
以地平面所在直线为x轴建立平面直角坐标系,
摩天轮的最高点距地面128米,摩天轮的半径为60米,摩天轮的圆心O到地面的距离为68米.
因为每转动一圈需要t分钟,所以.
.
(2)依题意,可知,即,
不妨取第一圈,可得,,
持续时间为,即,故t的最小值为25
同课章节目录
