7年级上册数学人教版课时练《4.1.2 点、线、面、体》(word、含答案)
文档属性
| 名称 | 7年级上册数学人教版课时练《4.1.2 点、线、面、体》(word、含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览

文档简介
人教版七年级数学上册
第四章 几何图形初步
《4,1,2 点、线、面、体》课时练
一、选择题
1.下列有六个面的几何体的个数是( )
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱
A.1个 B.2个 C.3个 D.4个
2.在以下四个几何体中,其侧面展开图不是平面图形的是( )
A.圆柱 B.棱柱 C.球 D.圆锥
3.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
4.用一个平面去截正方体,所得的截面不可能是( )
A.六边形 B.菱形 C.梯形 D.直角三角形
5.下列说法中,正确的是( )
A.棱柱的侧面可以是三角形
B.有两个面平行,其余各面都是四边形的几何体叫棱柱
C.将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥
D.棱台的侧棱所在的直线交于一点
6.下列现象不能体现线动成面的是( )
A.用平口铲子铲去墙面上的大片污渍
B.用一条拉直的细线切一块豆腐
C.流星划过天空留下运动轨迹
D.用木板的边缘将沙坑里的沙推平
7.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
8.下面几何体截面一定是圆的是( )
A.圆柱 B.圆锥 C.球 D.圆台
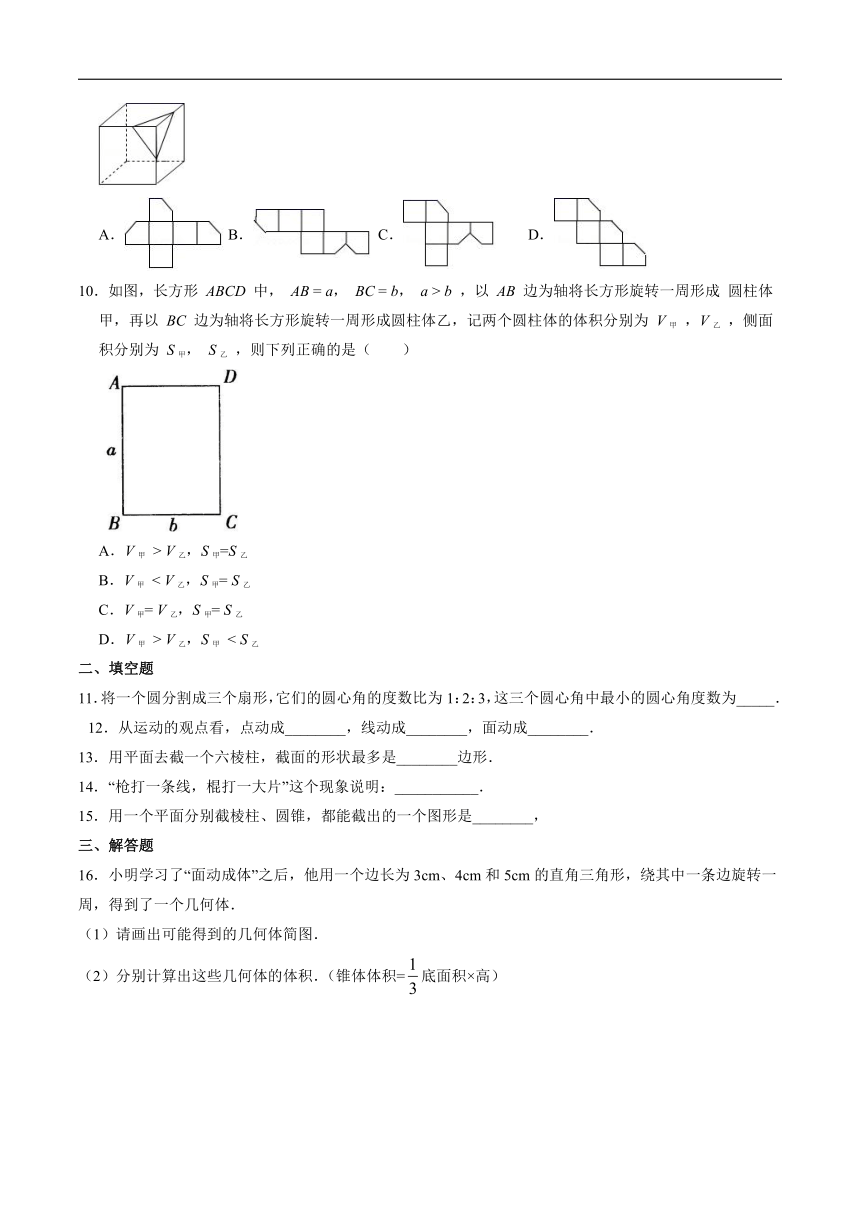
9.如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
A. B. C. D.
10.如图,长方形 ABCD 中, AB = a, BC = b, a > b ,以 AB 边为轴将长方形旋转一周形成 圆柱体甲,再以 BC 边为轴将长方形旋转一周形成圆柱体乙,记两个圆柱体的体积分别为 V甲 ,V乙 ,侧面积分别为 S甲, S乙 ,则下列正确的是( )
A.V甲 > V乙,S甲=S乙
B.V甲 < V乙,S甲= S乙
C.V甲= V乙,S甲= S乙
D.V甲 > V乙,S甲 < S乙
二、填空题
11.将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最小的圆心角度数为_____.
12.从运动的观点看,点动成________,线动成________,面动成________.
13.用平面去截一个六棱柱,截面的形状最多是________边形.
14.“枪打一条线,棍打一大片”这个现象说明:___________.
15.用一个平面分别截棱柱、圆锥,都能截出的一个图形是________,
三、解答题
16.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体简图.
(2)分别计算出这些几何体的体积.(锥体体积=底面积×高)
17.已知长方形的长为,宽为,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积,(结果保留)
18.一个圆柱的底面半径是6cm,高是12cm,如果用一个平面去截这个圆柱,截面能是正方形吗?如果能,请画图说明你的截法,并求这个正方形的面积;如果不能,请说明理由。
19.(1)把一个三棱柱分割成四个小三棱柱,你能找出多少种不同的分割方法?请把你的想法与同伴进行交流;
(2)在一个圆柱体中你能用一个平面截出一个三角形吗?能截出一个半圆吗?在什么条件下,你能截出一个正方形?
20.一个表面涂满色的正方体,现将棱三等分,再把它切开变成若干个小正方体,问:其中三面都涂色的小正方体有多少个?两面都涂色的小正方体有多少个?只有一面涂色的小正方体有多少个?各面都没有涂色的小正方体有多少个?
21.如果用平面截掉一个长方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?
22.用一个平面去截一个圆柱,(1)所得截面可能是三角形吗?(2)如果能得到正方形的截面,那么圆柱的底面半径和高有什么关系?
23.用平面去截一个正方体,能得到一个等边三角形吗?能得到一个直角三角形或钝角三角形截面吗?(画出示意图)
参考答案
1.C 2.C 3.D 4.D 5.D 6.C 7.B 8.C 9.D 10.B
11.60°
12.线 面 体
13.八
14.点动成线,线动成面
15.三角形
16.(1)以4cm为轴,得
;
以3cm为轴,得
;
以5cm为轴,得
;
(2)以4cm为轴体积为×π×32×4=12π,
以3cm为轴的体积为×π×42×3=16π,
以5cm为轴的体积为×π()2×5=9,6π.
17.(1)或;(2)或
18.能,截面能是正方形,经过底面圆心,顺着圆柱高的方向截圆柱,截面即为边长为12cm的正方形,
正方形的面积为,
19.(1)分割方法有:①横割三次;②横割一次,竖割一次;③竖割三次等
(2)不能截出三角形;不能截出半圆;圆柱的高等于底面圆的直径时,能截出一个正方形,
20.8,12,6,1
21.解:剩下的几何体可能有:7个顶点、12条棱、7个面;
或8个顶点、13条棱、7个面;
或9个顶点、14条棱、7个面;
或10个顶点、15条棱、7个面.
如图所示:
22.(1)不可能(2)底面半径是高的一半
23.能,不能,不能
第四章 几何图形初步
《4,1,2 点、线、面、体》课时练
一、选择题
1.下列有六个面的几何体的个数是( )
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱
A.1个 B.2个 C.3个 D.4个
2.在以下四个几何体中,其侧面展开图不是平面图形的是( )
A.圆柱 B.棱柱 C.球 D.圆锥
3.下列说法错误的是( )
A.若棱柱的底面边长相等,则它的各个侧面的面积相等
B.正九棱柱有9条侧棱,9个侧面,侧面为长方形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形
4.用一个平面去截正方体,所得的截面不可能是( )
A.六边形 B.菱形 C.梯形 D.直角三角形
5.下列说法中,正确的是( )
A.棱柱的侧面可以是三角形
B.有两个面平行,其余各面都是四边形的几何体叫棱柱
C.将直角三角形绕它的一边所在的直线旋转一周,形成的几何体一定是圆锥
D.棱台的侧棱所在的直线交于一点
6.下列现象不能体现线动成面的是( )
A.用平口铲子铲去墙面上的大片污渍
B.用一条拉直的细线切一块豆腐
C.流星划过天空留下运动轨迹
D.用木板的边缘将沙坑里的沙推平
7.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是( )
A.①②③④ B.①②③ C.②③④ D.①③④
8.下面几何体截面一定是圆的是( )
A.圆柱 B.圆锥 C.球 D.圆台
9.如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
A. B. C. D.
10.如图,长方形 ABCD 中, AB = a, BC = b, a > b ,以 AB 边为轴将长方形旋转一周形成 圆柱体甲,再以 BC 边为轴将长方形旋转一周形成圆柱体乙,记两个圆柱体的体积分别为 V甲 ,V乙 ,侧面积分别为 S甲, S乙 ,则下列正确的是( )
A.V甲 > V乙,S甲=S乙
B.V甲 < V乙,S甲= S乙
C.V甲= V乙,S甲= S乙
D.V甲 > V乙,S甲 < S乙
二、填空题
11.将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,这三个圆心角中最小的圆心角度数为_____.
12.从运动的观点看,点动成________,线动成________,面动成________.
13.用平面去截一个六棱柱,截面的形状最多是________边形.
14.“枪打一条线,棍打一大片”这个现象说明:___________.
15.用一个平面分别截棱柱、圆锥,都能截出的一个图形是________,
三、解答题
16.小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体简图.
(2)分别计算出这些几何体的体积.(锥体体积=底面积×高)
17.已知长方形的长为,宽为,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积,(结果保留)
18.一个圆柱的底面半径是6cm,高是12cm,如果用一个平面去截这个圆柱,截面能是正方形吗?如果能,请画图说明你的截法,并求这个正方形的面积;如果不能,请说明理由。
19.(1)把一个三棱柱分割成四个小三棱柱,你能找出多少种不同的分割方法?请把你的想法与同伴进行交流;
(2)在一个圆柱体中你能用一个平面截出一个三角形吗?能截出一个半圆吗?在什么条件下,你能截出一个正方形?
20.一个表面涂满色的正方体,现将棱三等分,再把它切开变成若干个小正方体,问:其中三面都涂色的小正方体有多少个?两面都涂色的小正方体有多少个?只有一面涂色的小正方体有多少个?各面都没有涂色的小正方体有多少个?
21.如果用平面截掉一个长方体的一个角,剩下的几何体有几个顶点、几条棱、几个面?
22.用一个平面去截一个圆柱,(1)所得截面可能是三角形吗?(2)如果能得到正方形的截面,那么圆柱的底面半径和高有什么关系?
23.用平面去截一个正方体,能得到一个等边三角形吗?能得到一个直角三角形或钝角三角形截面吗?(画出示意图)
参考答案
1.C 2.C 3.D 4.D 5.D 6.C 7.B 8.C 9.D 10.B
11.60°
12.线 面 体
13.八
14.点动成线,线动成面
15.三角形
16.(1)以4cm为轴,得
;
以3cm为轴,得
;
以5cm为轴,得
;
(2)以4cm为轴体积为×π×32×4=12π,
以3cm为轴的体积为×π×42×3=16π,
以5cm为轴的体积为×π()2×5=9,6π.
17.(1)或;(2)或
18.能,截面能是正方形,经过底面圆心,顺着圆柱高的方向截圆柱,截面即为边长为12cm的正方形,
正方形的面积为,
19.(1)分割方法有:①横割三次;②横割一次,竖割一次;③竖割三次等
(2)不能截出三角形;不能截出半圆;圆柱的高等于底面圆的直径时,能截出一个正方形,
20.8,12,6,1
21.解:剩下的几何体可能有:7个顶点、12条棱、7个面;
或8个顶点、13条棱、7个面;
或9个顶点、14条棱、7个面;
或10个顶点、15条棱、7个面.
如图所示:
22.(1)不可能(2)底面半径是高的一半
23.能,不能,不能
