1.3.1函数的单调性与导数 教学设计——2020-2021学年高二上学期数学人教A版选修2-2(表格式)
文档属性
| 名称 | 1.3.1函数的单调性与导数 教学设计——2020-2021学年高二上学期数学人教A版选修2-2(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览

文档简介
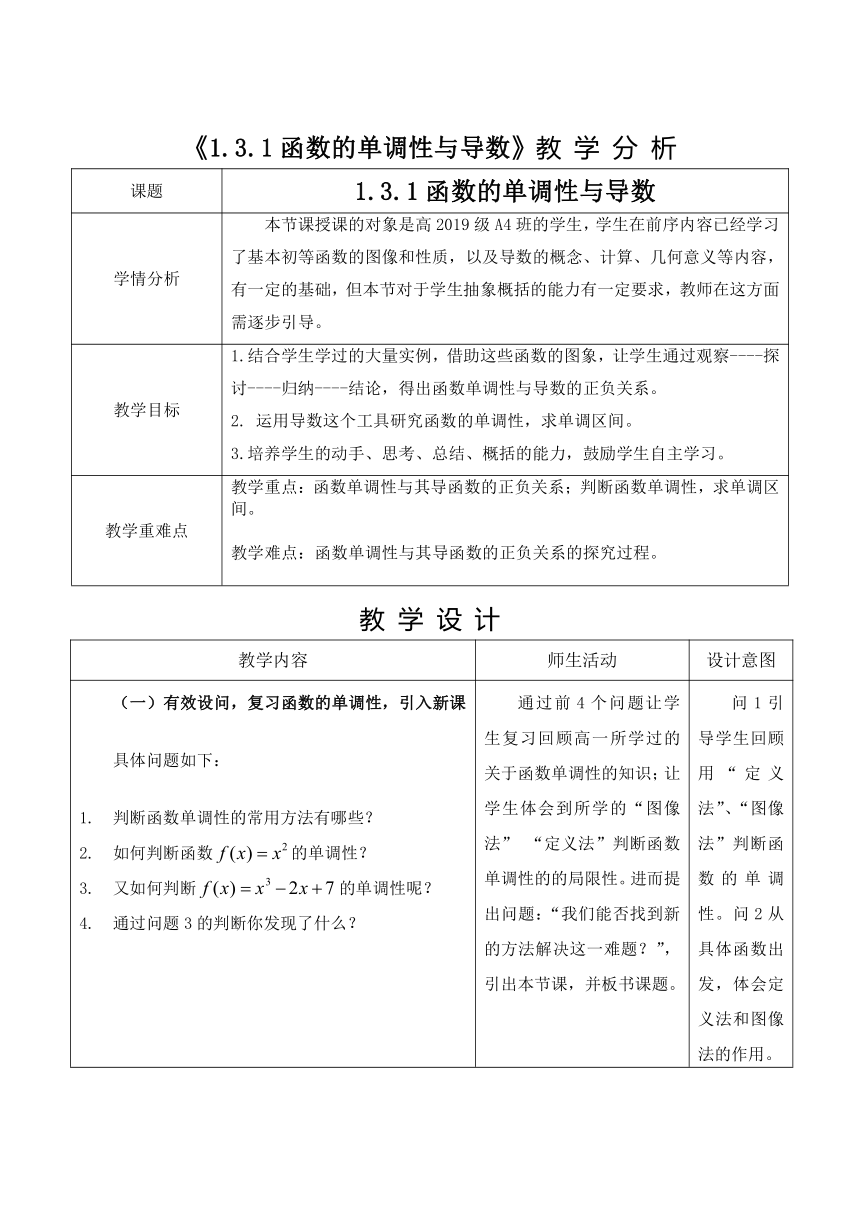
《1.3.1函数的单调性与导数》教 学 分 析
课题 1.3.1函数的单调性与导数
学情分析 本节课授课的对象是高2019级A4班的学生,学生在前序内容已经学习了基本初等函数的图像和性质,以及导数的概念、计算、几何意义等内容,有一定的基础,但本节对于学生抽象概括的能力有一定要求,教师在这方面需逐步引导。
教学目标 1.结合学生学过的大量实例,借助这些函数的图象,让学生通过观察----探讨----归纳----结论,得出函数单调性与导数的正负关系。 2. 运用导数这个工具研究函数的单调性,求单调区间。 3.培养学生的动手、思考、总结、概括的能力,鼓励学生自主学习。
教学重难点 教学重点:函数单调性与其导函数的正负关系;判断函数单调性,求单调区间。 教学难点:函数单调性与其导函数的正负关系的探究过程。
教 学 设 计
教学内容 师生活动 设计意图
(一)有效设问,复习函数的单调性,引入新课 具体问题如下: 判断函数单调性的常用方法有哪些? 如何判断函数的单调性? 又如何判断的单调性呢? 通过问题3的判断你发现了什么? 通过前4个问题让学生复习回顾高一所学过的关于函数单调性的知识;让学生体会到所学的“图像法” “定义法”判断函数单调性的的局限性。进而提出问题:“我们能否找到新的方法解决这一难题?”,引出本节课,并板书课题。 问1引导学生回顾用“定义法”、“图像法”判断函数的单调性。问2从具体函数出发,体会定义法和图像法的作用。
教学内容 师生活动 设计意图
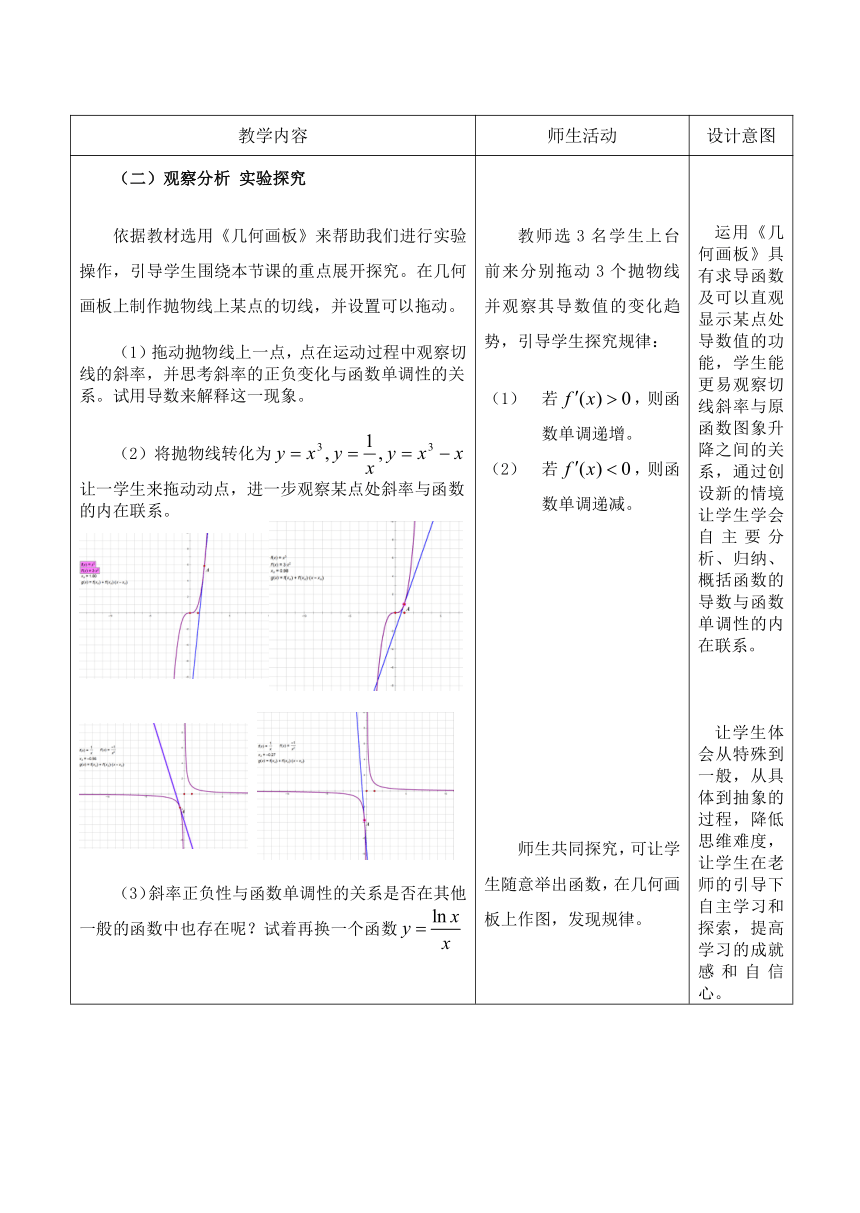
(二)观察分析 实验探究 依据教材选用《几何画板》来帮助我们进行实验操作,引导学生围绕本节课的重点展开探究。在几何画板上制作抛物线上某点的切线,并设置可以拖动。 (1)拖动抛物线上一点,点在运动过程中观察切线的斜率,并思考斜率的正负变化与函数单调性的关系。试用导数来解释这一现象。 (2)将抛物线转化为让一学生来拖动动点,进一步观察某点处斜率与函数的内在联系。 (3)斜率正负性与函数单调性的关系是否在其他一般的函数中也存在呢?试着再换一个函数 教师选3名学生上台前来分别拖动3个抛物线并观察其导数值的变化趋势,引导学生探究规律: 若,则函数单调递增。 若,则函数单调递减。 师生共同探究,可让学生随意举出函数,在几何画板上作图,发现规律。 运用《几何画板》具有求导函数及可以直观显示某点处导数值的功能,学生能更易观察切线斜率与原函数图象升降之间的关系,通过创设新的情境让学生学会自主要分析、归纳、概括函数的导数与函数单调性的内在联系。 让学生体会从特殊到一般,从具体到抽象的过程,降低思维难度,让学生在老师的引导下自主学习和探索,提高学习的成就感和自信心。
(三)追踪成果 深入探究 问1:那如果,函数又具备什么特征呢 问2:如果反过来,函数单调递增,成立吗?同样的,函数单调递减,成立吗? 问3:如果不成立,你能举出反例吗? (四)归纳结论,揭示本质 并板书结论:函数的单调性与其导函数正负的关系:在某个区间(a,b)内,若,则在(a,b)上是增函数;若,则在(a,b)上是减函数. 强调正确理解某个区间的含义,它必须是在定义域内的某个区间。反之,不成立。 (五)应用 例1已知函数的导函数的下列信息,试画出函数的大致图像。 当时, 当 当 例2 判断下列函数的单调性,并求出单调区间。 (1) (2) (3) (4) (六)课堂小结 内化知识 1.函数的单调性与其导函数正负的关系: 2.用导数求函数单调区间的一般步骤: 3.用导数的正负来判断函数的单调性,是导数几何意义在研究曲线变化规律的一个应用,它充分体现了数形结合的思想。 教师逐步追问,让学生有效思考该结论是否严谨。本质上我们只研究了结论的充分性,必要性还没研究。 教师引导学生探讨函数单调性与导数正负的充分必要关系,可举出。 采用由易到难,逐步过渡的教学策略,让学生进一步直观观察,分析问题的本质。
经历上述探究之后,将学生分成小组,进行讨论交流,揭示函数的单调性与导数的本质关系,让小组派代表归纳结论。 口头、书面的数学表达是学好数学的基本功
例1是一道逆向思维题,让学生动手操作,可以发现不同学生的理解程度,并及时纠正。其中例2老师板演,引导学生得出用导数法求单调区间的解题步骤,给学生示范,并将结果和利用“图象法”与“定义法”得到的结果进行比对,让学生进一步接受利用“导数法”求单调性; 师生共同总结,对于结论的充分不必要性教师重点指出,同时说明求单调区间的一般步骤。 通过本例的2个题目,从简单到复杂,让学生掌握用导数判断函数单调性的方法,并总结出一般步骤。
板书 设计 函数的单调性与导数 在某个区间(a,b)内,若,则在(a,b)上是增函数;若,则在(a,b)上是减函数. 例题
作业 布置 小聚焦
教 学 反 思
在教学实施过程中,备课是相当重要的,尤其是课堂活动中运用到的一些多媒体,要反复试用,避免出现问题,同时积极应对学生的突发状况。
课题 1.3.1函数的单调性与导数
学情分析 本节课授课的对象是高2019级A4班的学生,学生在前序内容已经学习了基本初等函数的图像和性质,以及导数的概念、计算、几何意义等内容,有一定的基础,但本节对于学生抽象概括的能力有一定要求,教师在这方面需逐步引导。
教学目标 1.结合学生学过的大量实例,借助这些函数的图象,让学生通过观察----探讨----归纳----结论,得出函数单调性与导数的正负关系。 2. 运用导数这个工具研究函数的单调性,求单调区间。 3.培养学生的动手、思考、总结、概括的能力,鼓励学生自主学习。
教学重难点 教学重点:函数单调性与其导函数的正负关系;判断函数单调性,求单调区间。 教学难点:函数单调性与其导函数的正负关系的探究过程。
教 学 设 计
教学内容 师生活动 设计意图
(一)有效设问,复习函数的单调性,引入新课 具体问题如下: 判断函数单调性的常用方法有哪些? 如何判断函数的单调性? 又如何判断的单调性呢? 通过问题3的判断你发现了什么? 通过前4个问题让学生复习回顾高一所学过的关于函数单调性的知识;让学生体会到所学的“图像法” “定义法”判断函数单调性的的局限性。进而提出问题:“我们能否找到新的方法解决这一难题?”,引出本节课,并板书课题。 问1引导学生回顾用“定义法”、“图像法”判断函数的单调性。问2从具体函数出发,体会定义法和图像法的作用。
教学内容 师生活动 设计意图
(二)观察分析 实验探究 依据教材选用《几何画板》来帮助我们进行实验操作,引导学生围绕本节课的重点展开探究。在几何画板上制作抛物线上某点的切线,并设置可以拖动。 (1)拖动抛物线上一点,点在运动过程中观察切线的斜率,并思考斜率的正负变化与函数单调性的关系。试用导数来解释这一现象。 (2)将抛物线转化为让一学生来拖动动点,进一步观察某点处斜率与函数的内在联系。 (3)斜率正负性与函数单调性的关系是否在其他一般的函数中也存在呢?试着再换一个函数 教师选3名学生上台前来分别拖动3个抛物线并观察其导数值的变化趋势,引导学生探究规律: 若,则函数单调递增。 若,则函数单调递减。 师生共同探究,可让学生随意举出函数,在几何画板上作图,发现规律。 运用《几何画板》具有求导函数及可以直观显示某点处导数值的功能,学生能更易观察切线斜率与原函数图象升降之间的关系,通过创设新的情境让学生学会自主要分析、归纳、概括函数的导数与函数单调性的内在联系。 让学生体会从特殊到一般,从具体到抽象的过程,降低思维难度,让学生在老师的引导下自主学习和探索,提高学习的成就感和自信心。
(三)追踪成果 深入探究 问1:那如果,函数又具备什么特征呢 问2:如果反过来,函数单调递增,成立吗?同样的,函数单调递减,成立吗? 问3:如果不成立,你能举出反例吗? (四)归纳结论,揭示本质 并板书结论:函数的单调性与其导函数正负的关系:在某个区间(a,b)内,若,则在(a,b)上是增函数;若,则在(a,b)上是减函数. 强调正确理解某个区间的含义,它必须是在定义域内的某个区间。反之,不成立。 (五)应用 例1已知函数的导函数的下列信息,试画出函数的大致图像。 当时, 当 当 例2 判断下列函数的单调性,并求出单调区间。 (1) (2) (3) (4) (六)课堂小结 内化知识 1.函数的单调性与其导函数正负的关系: 2.用导数求函数单调区间的一般步骤: 3.用导数的正负来判断函数的单调性,是导数几何意义在研究曲线变化规律的一个应用,它充分体现了数形结合的思想。 教师逐步追问,让学生有效思考该结论是否严谨。本质上我们只研究了结论的充分性,必要性还没研究。 教师引导学生探讨函数单调性与导数正负的充分必要关系,可举出。 采用由易到难,逐步过渡的教学策略,让学生进一步直观观察,分析问题的本质。
经历上述探究之后,将学生分成小组,进行讨论交流,揭示函数的单调性与导数的本质关系,让小组派代表归纳结论。 口头、书面的数学表达是学好数学的基本功
例1是一道逆向思维题,让学生动手操作,可以发现不同学生的理解程度,并及时纠正。其中例2老师板演,引导学生得出用导数法求单调区间的解题步骤,给学生示范,并将结果和利用“图象法”与“定义法”得到的结果进行比对,让学生进一步接受利用“导数法”求单调性; 师生共同总结,对于结论的充分不必要性教师重点指出,同时说明求单调区间的一般步骤。 通过本例的2个题目,从简单到复杂,让学生掌握用导数判断函数单调性的方法,并总结出一般步骤。
板书 设计 函数的单调性与导数 在某个区间(a,b)内,若,则在(a,b)上是增函数;若,则在(a,b)上是减函数. 例题
作业 布置 小聚焦
教 学 反 思
在教学实施过程中,备课是相当重要的,尤其是课堂活动中运用到的一些多媒体,要反复试用,避免出现问题,同时积极应对学生的突发状况。
