2021-2022学年青岛版九年级数学上册 2.4.1解直角三角形 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册 2.4.1解直角三角形 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 19:21:48 | ||
图片预览





文档简介
(共15张PPT)
2.5.1解直角三角形
学习目标
(1)我要了解解直角三角形的意义和条件
(2)我能根据直角三角形中除直角外的两个元素(至少有一个是边)解直角三角形
(3)通过解直角三角形,感悟数学中的转化思想
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据:
A
C
B
a
b
c
a2+b2=c2(勾股定理);
(1)三边之间的关系:
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
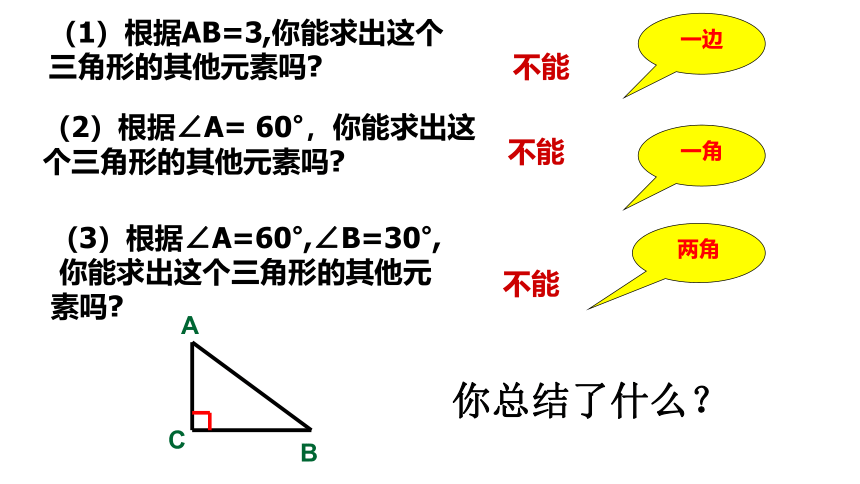
不能
不能
一角
A
B
C
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
(2)根据∠A= 60°,你能求出这个三角形的其他元素吗
(1)根据AB=3,你能求出这个三角形的其他元素吗
不能
一边
你总结了什么?
两角
已知一条边、一个角或者两角 不能求其它元素
一角
一边
总结规律:
A
B
C
(3)根据BC=2 ,AC= 2 ,
你能求出这个三角形的其他元素吗?
两边
AB ∠A ∠B
一角一边
A
B
C
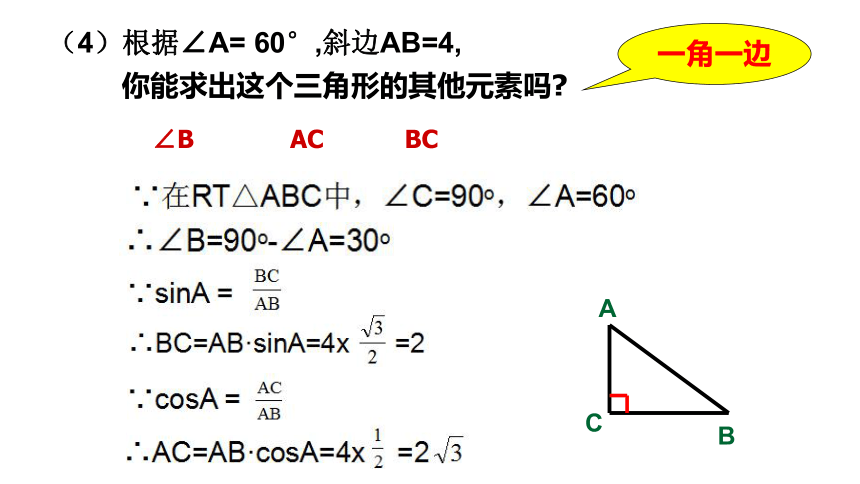
(4)根据∠A= 60°,斜边AB=4,
你能求出这个三角形的其他元素吗
∠B AC BC
一角一边
两边
已知一角一边或两边能求其它元素
总结规律:
(其中至少有一个是边),
在直角三角形的六个元素中,除直角外,如果知道两个元素, 就可以求出其余三个元素.
一角一边
两边
两角
不能求其它元素
一角
能求其它元素
一边
小结:
解:
A
B
C
(2)在Rt△ABC中,∠C=90°,AC= ,BC= ,
解这个直角三角形.
∵ tanA= = =
BC
AB
∴
∠A=60°,
∠B=90°— ∠A
= 90°— 60°= 30°,
AB = 2AC =2
(1)、Rt△ABC中, ∠C=90°,若sinA= ,AB=10,
那么BC=_____,tanB=______.
8
(3)在Rt△ABC,∠C=90°, ∠A=45°,c=4 解这个直角三角形.
C
B
A
c
解:
∵ ∠A=45°
∴ ∠B=90°—∠A=45°,
sinA=
a
c
∵
a= sinA·c= sin 45°·4= ·4=2
2
∴
cosA=
b
c
∵
b=cosA·c=cos 45°·4= ·4=2
2
∴
a
b
锐角三角函数关系式的变形:
sinA=
a
c
cosA=
b
c
tanA=
a
b
·
a= sinA·c
b= cosA·c
a= tanA·b
c=
a
sinA
b=
a
tanA
c=
b
cosA
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
2、 在Rt△ABC中,∠C=90 ,
解这个直角三角形
A
C
B
a
b
c
1.在四边形ABCD中,∠ A= ,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD,BC的长(保留根号)?
60°
E
B
A
C
D
20
10
60°
30°
的平分线AD=4
(3)在Rt△ABC中,∠C为直角,AC=6,
,解此直角三角形。
60
30
6
12
30
A
D
B
C
2.5.1解直角三角形
学习目标
(1)我要了解解直角三角形的意义和条件
(2)我能根据直角三角形中除直角外的两个元素(至少有一个是边)解直角三角形
(3)通过解直角三角形,感悟数学中的转化思想
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据:
A
C
B
a
b
c
a2+b2=c2(勾股定理);
(1)三边之间的关系:
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
不能
不能
一角
A
B
C
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
(2)根据∠A= 60°,你能求出这个三角形的其他元素吗
(1)根据AB=3,你能求出这个三角形的其他元素吗
不能
一边
你总结了什么?
两角
已知一条边、一个角或者两角 不能求其它元素
一角
一边
总结规律:
A
B
C
(3)根据BC=2 ,AC= 2 ,
你能求出这个三角形的其他元素吗?
两边
AB ∠A ∠B
一角一边
A
B
C
(4)根据∠A= 60°,斜边AB=4,
你能求出这个三角形的其他元素吗
∠B AC BC
一角一边
两边
已知一角一边或两边能求其它元素
总结规律:
(其中至少有一个是边),
在直角三角形的六个元素中,除直角外,如果知道两个元素, 就可以求出其余三个元素.
一角一边
两边
两角
不能求其它元素
一角
能求其它元素
一边
小结:
解:
A
B
C
(2)在Rt△ABC中,∠C=90°,AC= ,BC= ,
解这个直角三角形.
∵ tanA= = =
BC
AB
∴
∠A=60°,
∠B=90°— ∠A
= 90°— 60°= 30°,
AB = 2AC =2
(1)、Rt△ABC中, ∠C=90°,若sinA= ,AB=10,
那么BC=_____,tanB=______.
8
(3)在Rt△ABC,∠C=90°, ∠A=45°,c=4 解这个直角三角形.
C
B
A
c
解:
∵ ∠A=45°
∴ ∠B=90°—∠A=45°,
sinA=
a
c
∵
a= sinA·c= sin 45°·4= ·4=2
2
∴
cosA=
b
c
∵
b=cosA·c=cos 45°·4= ·4=2
2
∴
a
b
锐角三角函数关系式的变形:
sinA=
a
c
cosA=
b
c
tanA=
a
b
·
a= sinA·c
b= cosA·c
a= tanA·b
c=
a
sinA
b=
a
tanA
c=
b
cosA
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角 B、已知一斜边一锐角
C、已知两边 D、已知两角
2、 在Rt△ABC中,∠C=90 ,
解这个直角三角形
A
C
B
a
b
c
1.在四边形ABCD中,∠ A= ,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD,BC的长(保留根号)?
60°
E
B
A
C
D
20
10
60°
30°
的平分线AD=4
(3)在Rt△ABC中,∠C为直角,AC=6,
,解此直角三角形。
60
30
6
12
30
A
D
B
C
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
