2021-2022学年青岛版九年级数学上册 3.1.2 圆的对称性 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册 3.1.2 圆的对称性 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 169.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
3.1.2圆的对称性
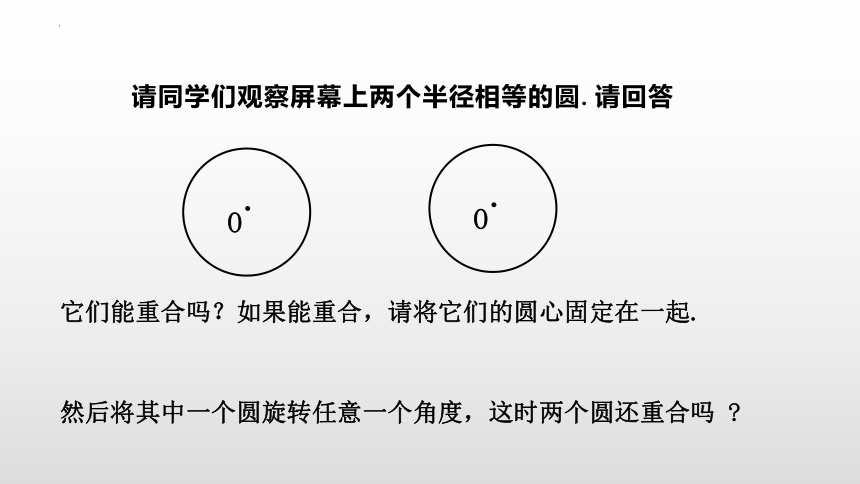
请同学们观察屏幕上两个半径相等的圆.请回答
O
O
它们能重合吗?如果能重合,请将它们的圆心固定在一起.
然后将其中一个圆旋转任意一个角度,这时两个圆还重合吗
(1)圆是 圆形, 是它的对称中心
(2) 在 中,如果两个圆心角、两条弧、两条弦、两条弦心距中有 量相等,那么它们所对应其余各组量都分别分别相等(即“知一推三”)
(3)在⊙O中画∠AOB=∠A'OB' ,连接AB、A'B',作OD⊥AB、OD'⊥A'B',
∵∠AOB=∠A'OB' ,∴ 、 、 ;
∵ ⌒ = ⌒ , ∴ 、 、 ;
∵ AB=A'B' , ∴ 、 、 ;
∵ OD=OD' , ∴ 、 、 .
(4)圆心角的度数与它所对弧的度数 .
自主完成
AB
A'B'
中心对称
圆心
同圆或等圆
一组
相等
归纳
圆具有旋转不变性,即一个圆绕着它的圆心旋转任意一个角度,都能与原来的圆重合.因此,圆是中心对称圆形,圆心是它的对称中心.圆的中心对称性是其旋转不变性的特例.
1、两半径相等的圆,在⊙O 和⊙O′上分别作相等的圆心角 ∠A O B和∠A′O′B′,然后将两圆的圆心固定在一起.
2、将其中的一个圆旋转一个角度,使得O A与O′A′重合
A′
B′
O′
A
B
O
你能从中发现哪些等量关系 (从圆心角、弧、弦考虑)
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
1、在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗 你是怎么想的?
2、在同圆或等到圆中,如果两条弦相等,那么它们所对的圆心角相等吗?它们所对的弧相等吗?你是怎么想的?
A
B
O
B′
A′
O′
如图所示:
(1)∵⊙O 和⊙O′是等圆
且∠A O B=∠A′O′B′,
∴A B=A′B′,A B= A′B′.
∵⊙O 和⊙O′是等圆且A B= A′B′
∴ A B=A′B′,∠A O B=∠A′O′B′.
(2)
∵⊙O 和⊙O′是等圆且A B= A′B′
∴ A B=A′B′,∠A O B=∠A′O′B′.
(3)
定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、中有一组量相等,那么它们所对应其余各组量都分别分别相等(知一推二)
推论:在同圆或等圆中,相等的两条弦的两条弦心距(垂线段)也相等(知一推三)
例题3
如图 ,AB 与 DE 是⊙O 的两条直径,C 是⊙O 上一点,AC∥DE . 求证:(1)AD = CE; (2)BE = EC .
(1)连接OC
∵ AC∥DE,
∴∠AOD =∠OAC, ∠COE =∠OCA ∵ OA = OC
∴∠OAC =∠OCA
∴∠AOD =∠COE
∴ AD = CE
(2)∵∠AOD =∠BOE
∴∠BOE =∠COE ∴ BE = CE
(1)把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少?
(2)把顶点在圆心的周角等分为 360 份时,整个圆被分成了多少份?每一份的弧是否相等?为什么?
每一份圆心角的度数是1
整个圆被分成了360份,且每一份的弧都相等,因为每一份弧所对的圆心角都相等
整个圆的 叫做 1°的弧. 因此,1°的圆心角所对的弧是 1°的弧;反之,1°的弧所对的圆心角是 1°的角. 一般地,n°的圆心角所对的弧是 n°的弧;反之, n°的弧所对的圆心角是 n°的角. 由此可见,圆心角与它所对的弧有以下关系:
圆心角的度数与它所对弧的度数相等.
课堂巩固
(1)下列命题中,真命题是( )
A.相等的圆心角所对的弧相等 B.相等的弦所对的弧相等
C.度数相等的弧是等弧 D.相等的弧所对弦相等
2.填空题:
(1)一条弦把圆分成1:3两部分,则弦所对的圆心角为 .
(2)如图,AB是⊙O的直径,BC = CD = DE,∠BOC=40°,
则∠AOE的度数是 度.
3.解答题:
(1)如图,在⊙O中,AB=AC,∠A=40°,求∠B的度数.
(2)如图,AB、CD是⊙O的直径,弦CE∥AB,CE的度数为40°,求∠AOC的度数.
(3)如图,点A、B、C、D在⊙O上,AB=DC,AC与BD相等吗?为什么?
3.1.2圆的对称性
请同学们观察屏幕上两个半径相等的圆.请回答
O
O
它们能重合吗?如果能重合,请将它们的圆心固定在一起.
然后将其中一个圆旋转任意一个角度,这时两个圆还重合吗
(1)圆是 圆形, 是它的对称中心
(2) 在 中,如果两个圆心角、两条弧、两条弦、两条弦心距中有 量相等,那么它们所对应其余各组量都分别分别相等(即“知一推三”)
(3)在⊙O中画∠AOB=∠A'OB' ,连接AB、A'B',作OD⊥AB、OD'⊥A'B',
∵∠AOB=∠A'OB' ,∴ 、 、 ;
∵ ⌒ = ⌒ , ∴ 、 、 ;
∵ AB=A'B' , ∴ 、 、 ;
∵ OD=OD' , ∴ 、 、 .
(4)圆心角的度数与它所对弧的度数 .
自主完成
AB
A'B'
中心对称
圆心
同圆或等圆
一组
相等
归纳
圆具有旋转不变性,即一个圆绕着它的圆心旋转任意一个角度,都能与原来的圆重合.因此,圆是中心对称圆形,圆心是它的对称中心.圆的中心对称性是其旋转不变性的特例.
1、两半径相等的圆,在⊙O 和⊙O′上分别作相等的圆心角 ∠A O B和∠A′O′B′,然后将两圆的圆心固定在一起.
2、将其中的一个圆旋转一个角度,使得O A与O′A′重合
A′
B′
O′
A
B
O
你能从中发现哪些等量关系 (从圆心角、弧、弦考虑)
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
1、在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗 你是怎么想的?
2、在同圆或等到圆中,如果两条弦相等,那么它们所对的圆心角相等吗?它们所对的弧相等吗?你是怎么想的?
A
B
O
B′
A′
O′
如图所示:
(1)∵⊙O 和⊙O′是等圆
且∠A O B=∠A′O′B′,
∴A B=A′B′,A B= A′B′.
∵⊙O 和⊙O′是等圆且A B= A′B′
∴ A B=A′B′,∠A O B=∠A′O′B′.
(2)
∵⊙O 和⊙O′是等圆且A B= A′B′
∴ A B=A′B′,∠A O B=∠A′O′B′.
(3)
定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、中有一组量相等,那么它们所对应其余各组量都分别分别相等(知一推二)
推论:在同圆或等圆中,相等的两条弦的两条弦心距(垂线段)也相等(知一推三)
例题3
如图 ,AB 与 DE 是⊙O 的两条直径,C 是⊙O 上一点,AC∥DE . 求证:(1)AD = CE; (2)BE = EC .
(1)连接OC
∵ AC∥DE,
∴∠AOD =∠OAC, ∠COE =∠OCA ∵ OA = OC
∴∠OAC =∠OCA
∴∠AOD =∠COE
∴ AD = CE
(2)∵∠AOD =∠BOE
∴∠BOE =∠COE ∴ BE = CE
(1)把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少?
(2)把顶点在圆心的周角等分为 360 份时,整个圆被分成了多少份?每一份的弧是否相等?为什么?
每一份圆心角的度数是1
整个圆被分成了360份,且每一份的弧都相等,因为每一份弧所对的圆心角都相等
整个圆的 叫做 1°的弧. 因此,1°的圆心角所对的弧是 1°的弧;反之,1°的弧所对的圆心角是 1°的角. 一般地,n°的圆心角所对的弧是 n°的弧;反之, n°的弧所对的圆心角是 n°的角. 由此可见,圆心角与它所对的弧有以下关系:
圆心角的度数与它所对弧的度数相等.
课堂巩固
(1)下列命题中,真命题是( )
A.相等的圆心角所对的弧相等 B.相等的弦所对的弧相等
C.度数相等的弧是等弧 D.相等的弧所对弦相等
2.填空题:
(1)一条弦把圆分成1:3两部分,则弦所对的圆心角为 .
(2)如图,AB是⊙O的直径,BC = CD = DE,∠BOC=40°,
则∠AOE的度数是 度.
3.解答题:
(1)如图,在⊙O中,AB=AC,∠A=40°,求∠B的度数.
(2)如图,AB、CD是⊙O的直径,弦CE∥AB,CE的度数为40°,求∠AOC的度数.
(3)如图,点A、B、C、D在⊙O上,AB=DC,AC与BD相等吗?为什么?
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
