2021-2022学年青岛版九年级数学上册3.1.1圆的对称性 课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年青岛版九年级数学上册3.1.1圆的对称性 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
3.1.1圆的对称性
1.圆是轴对称图形,经过_______的每一条______都是它的对称轴。
圆心
直线
2.垂径定理:垂直于弦的直径平分弦以及___________________。
平分弦所对的两条弧
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
O
A
C
B
N
M
D
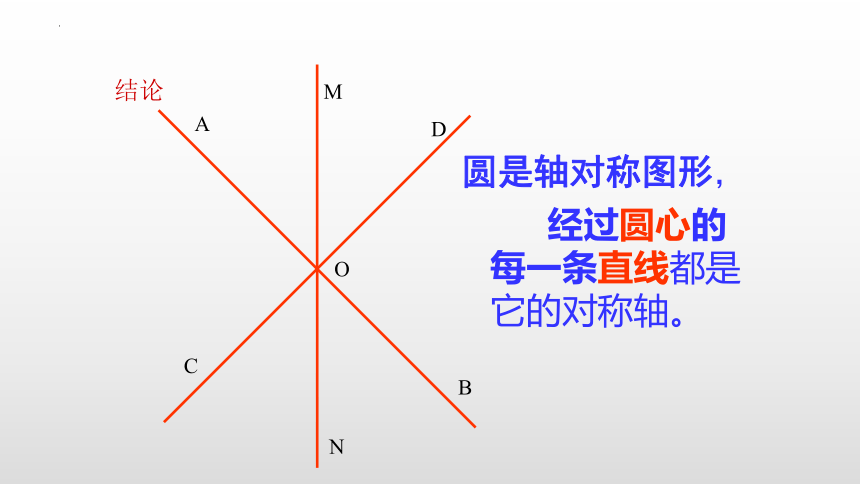
圆是轴对称图形,
经过圆心的每一条直线都是它的对称轴。
结论
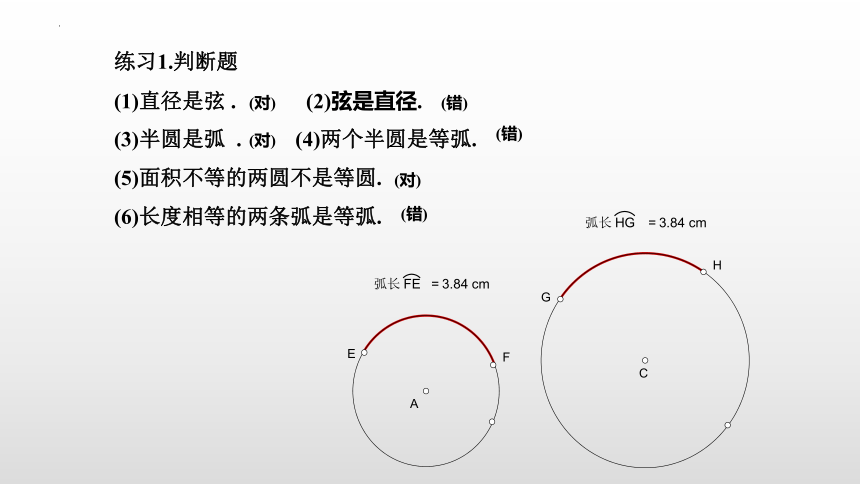
练习1.判断题
(1)直径是弦 . (2)弦是直径.
(3)半圆是弧 . (4)两个半圆是等弧.
(5)面积不等的两圆不是等圆.
(6)长度相等的两条弧是等弧.
A
C
E
F
G
H
弧长
FE
=
3.84 cm
弧长
HG
=
3.84 cm
(对)
(错)
(错)
(对)
(对)
(错)
思路:
与证明相似三角形的判定定理 1,2 类似,如果能在△ABC 中用平行于 BC 边的直线截得一个△ADE,使它与△A'B'C' 全等,并与△ABC相似,问题就可以解决。
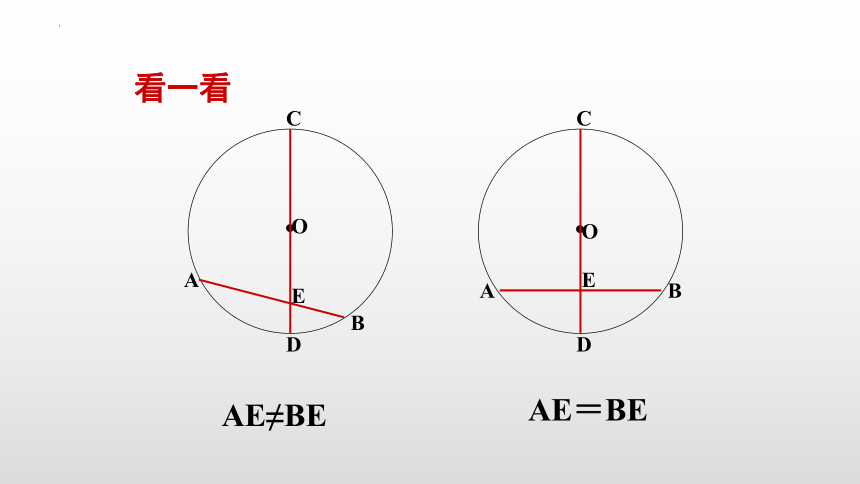
看一看
B
.
O
C
A
E
D
O
.
C
A
E
B
D
AE≠BE
AE=BE
AB是⊙O的一条弦
作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗 如果是,其对称轴是什么
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
●O
C
D
M└
A
B
题设
结论
① CD是直径
② CD⊥AB
可推得
③AM=BM,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图,小明的理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
垂径定理
垂直于弦的直径平分弦以及平分弦所对的两条弧.
题设
结论
(1)直径
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
垂径定理三种语言
定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
知识拓展:
所对圆心角大于180°的圆弧叫做优弧。
与优弧相对的是"劣弧",即小于180°的弧。
同弧或等弧所对圆周角相等。
半圆既不是优弧也不是劣弧,而是与其并列的一个概念。
也就是说圆弧分三类,优弧、劣弧、半圆。
在同圆或等圆中,能够互相重合的弧叫做等弧。
总结:
1.圆的对称性:圆的对称性有无数条;圆的对称线是直径所在的直线,而不是直径。
2.垂径定理:在垂径定理中,一是隐含着一条直线;二是该直线具有以下性质:①经过圆心;②垂直于弦;③平分这条弦;④平分这条弦所对的劣弧;⑤平分这条弦所对的优弧。
随堂检测
1. P是⊙O半径上一点,OP = 5, 经过点P的最短的弦长为24, 则⊙O的半径为 _______.
(2)如图3-1,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP∶PB = 1∶4, CD = 8, 则AB 的长为= _______.
(3)如图3-2,⊙O的半径为25cm,弦AB = 48cm, OD⊥AB于C交⊙O于D, 则AD = _____ .
13
10
30
(4) 已知:、是⊙O的两条劣弧,且= 2,则弦AB与CD之间的关系为( )
A. AB = 2CD B. AB < 2CD
C. AB > 2CD D. 不能确定
(5) 下列说法中,正确的是( )
A. 相等的圆心角所对的弧相等 B. 相等的圆心角所对的弦相等
C. 相等的弧所对的弦相等 D. 相等的弦所对的弧相等
B
C
1.“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图3-3,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( ).
A. 12.5寸 B. 13寸 C. 25寸 D. 26寸
D
2.已知:如图3-4,AB是⊙O的弦,P是AB上一点,AB = 10 cm, PA = 4 cm, OP = 5 cm, 求⊙O的半径.
3.已知:如图3-5,在⊙O中,弦AB的长是半径OA的 倍,C为的中点,AB、OC相交于点P,试判断:四边形OACB是何种特殊的四边形.
3.1.1圆的对称性
1.圆是轴对称图形,经过_______的每一条______都是它的对称轴。
圆心
直线
2.垂径定理:垂直于弦的直径平分弦以及___________________。
平分弦所对的两条弧
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
O
A
C
B
N
M
D
圆是轴对称图形,
经过圆心的每一条直线都是它的对称轴。
结论
练习1.判断题
(1)直径是弦 . (2)弦是直径.
(3)半圆是弧 . (4)两个半圆是等弧.
(5)面积不等的两圆不是等圆.
(6)长度相等的两条弧是等弧.
A
C
E
F
G
H
弧长
FE
=
3.84 cm
弧长
HG
=
3.84 cm
(对)
(错)
(错)
(对)
(对)
(错)
思路:
与证明相似三角形的判定定理 1,2 类似,如果能在△ABC 中用平行于 BC 边的直线截得一个△ADE,使它与△A'B'C' 全等,并与△ABC相似,问题就可以解决。
看一看
B
.
O
C
A
E
D
O
.
C
A
E
B
D
AE≠BE
AE=BE
AB是⊙O的一条弦
作直径CD,使CD⊥AB,垂足为M.
下图是轴对称图形吗 如果是,其对称轴是什么
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
●O
C
D
M└
A
B
题设
结论
① CD是直径
② CD⊥AB
可推得
③AM=BM,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图,小明的理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
垂径定理
垂直于弦的直径平分弦以及平分弦所对的两条弧.
题设
结论
(1)直径
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
垂径定理三种语言
定理: 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
知识拓展:
所对圆心角大于180°的圆弧叫做优弧。
与优弧相对的是"劣弧",即小于180°的弧。
同弧或等弧所对圆周角相等。
半圆既不是优弧也不是劣弧,而是与其并列的一个概念。
也就是说圆弧分三类,优弧、劣弧、半圆。
在同圆或等圆中,能够互相重合的弧叫做等弧。
总结:
1.圆的对称性:圆的对称性有无数条;圆的对称线是直径所在的直线,而不是直径。
2.垂径定理:在垂径定理中,一是隐含着一条直线;二是该直线具有以下性质:①经过圆心;②垂直于弦;③平分这条弦;④平分这条弦所对的劣弧;⑤平分这条弦所对的优弧。
随堂检测
1. P是⊙O半径上一点,OP = 5, 经过点P的最短的弦长为24, 则⊙O的半径为 _______.
(2)如图3-1,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP∶PB = 1∶4, CD = 8, 则AB 的长为= _______.
(3)如图3-2,⊙O的半径为25cm,弦AB = 48cm, OD⊥AB于C交⊙O于D, 则AD = _____ .
13
10
30
(4) 已知:、是⊙O的两条劣弧,且= 2,则弦AB与CD之间的关系为( )
A. AB = 2CD B. AB < 2CD
C. AB > 2CD D. 不能确定
(5) 下列说法中,正确的是( )
A. 相等的圆心角所对的弧相等 B. 相等的圆心角所对的弦相等
C. 相等的弧所对的弦相等 D. 相等的弦所对的弧相等
B
C
1.“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图3-3,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( ).
A. 12.5寸 B. 13寸 C. 25寸 D. 26寸
D
2.已知:如图3-4,AB是⊙O的弦,P是AB上一点,AB = 10 cm, PA = 4 cm, OP = 5 cm, 求⊙O的半径.
3.已知:如图3-5,在⊙O中,弦AB的长是半径OA的 倍,C为的中点,AB、OC相交于点P,试判断:四边形OACB是何种特殊的四边形.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
