高二数学人教A版2019选择性必修第一册 2.5 直线与圆、圆与圆的位置关系 精品讲义(Word版含答案)
文档属性
| 名称 | 高二数学人教A版2019选择性必修第一册 2.5 直线与圆、圆与圆的位置关系 精品讲义(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-28 00:00:00 | ||
图片预览




文档简介
2.5 直线与圆、圆与圆的位置关系
【知识点梳理】
知识点一:直线与圆的位置关系
1.直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2.直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
知识点诠释:
(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.
(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.
(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.
知识点二:圆的切线方程的求法
1.点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率
的乘积等于,即.
法二:圆心到直线的距离等于半径.
2.点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
知识点诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是
.
知识点三:求直线被圆截得的弦长的方法
1.应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
2.利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
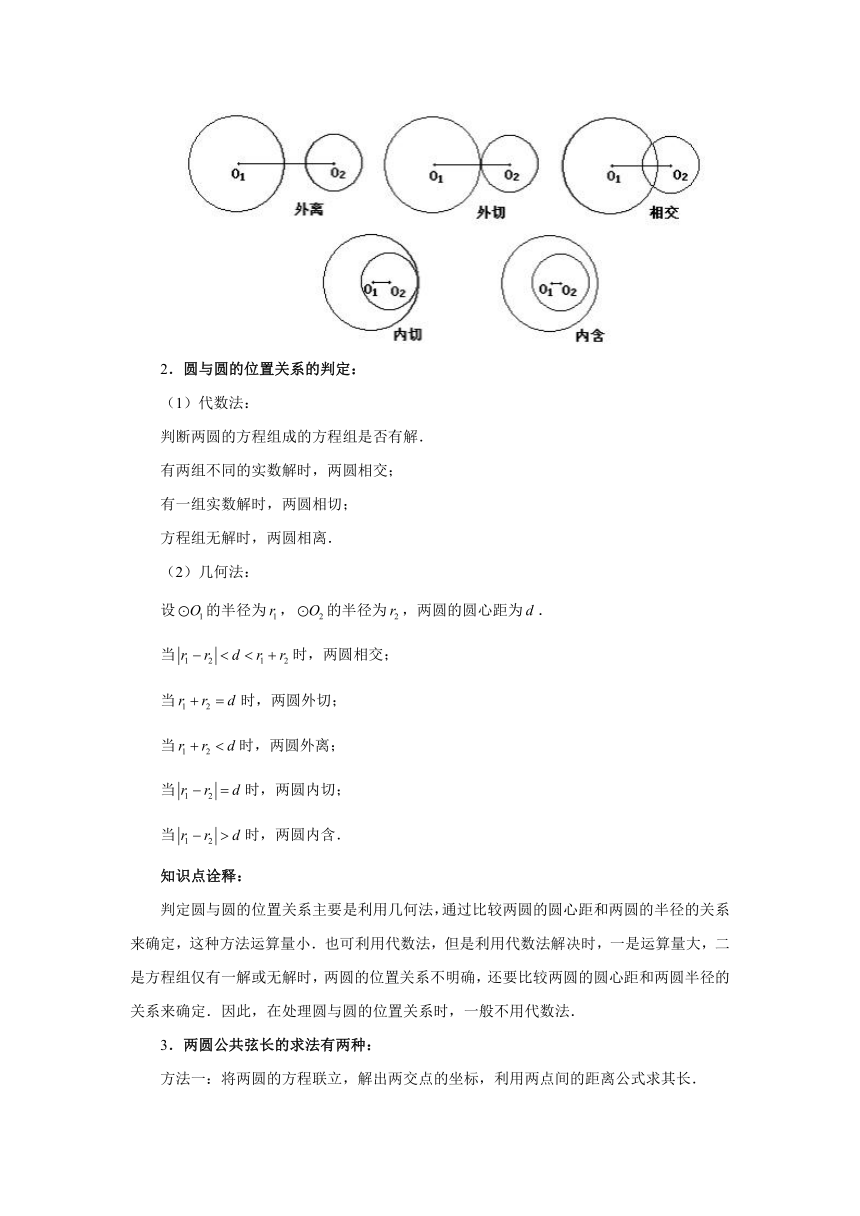
知识点四:圆与圆的位置关系
1.圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
2.圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
知识点诠释:
判定圆与圆的位置关系主要是利用几何法,通过比较两圆的圆心距和两圆的半径的关系来确定,这种方法运算量小.也可利用代数法,但是利用代数法解决时,一是运算量大,二是方程组仅有一解或无解时,两圆的位置关系不明确,还要比较两圆的圆心距和两圆半径的关系来确定.因此,在处理圆与圆的位置关系时,一般不用代数法.
3.两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
4.两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
【题型归纳目录】
题型一:不含参数(含参数)的直线与圆的位置关系
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
题型三:切线与切线长问题
题型四:弦长问题
题型五:判断圆与圆的位置关系
题型六:由圆的位置关系确定参数
题型七:公共弦与切点弦问题
题型八:公切线问题
题型九:圆中范围与最值问题
题型十:圆系问题
【典型例题】
题型一:不含参数(含参数)的直线与圆的位置关系
例1.(2022·全国·高二课时练习)直线和圆的位置关系为( )
A.相交 B.相切或相交 C.相离 D.相切
例2.(2022·西藏·林芝市第二高级中学高一期末)圆x2+y2-2x+4y=0与直线2x+y+1=0的位置关系为( )
A.相离 B.相切 C.相交 D.以上都有可能
例3.(2022·全国·高三专题练习)直线与圆的位置关系为( )
A.相切 B.相交
C.相离 D.由的取值确定
例4.(2022·全国·高二专题练习)圆与直线的位置关系为( )
A.相切 B.相离 C.相交 D.无法确定
【方法技巧与总结】
直线与圆的位置关系判断方法
法一抓住直线与圆的位置关系的代数特征,从而转化为对方程的解的研究,这是研究直线与曲线的位置关系的基本方法;法二抓住直线与圆的位置关系的几何特征,从而转化为研究圆心到直线的距离,抓住几何特征对于研究圆的问题特别有效;法三通过判定直线过圆内一定点,从而使问题获证.由上述三种解法可知,解题的切入点不同,解法就有优劣之分.因此,在解题时,审题要慢,要仔细地分析题意,透彻地理解题意,挖掘其中的隐含条件,从而找到解决问题的捷径.
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
例5.(2022·福建省福州第二中学高二期末)已知直线平分圆:,则的最大值为( )
A. B. C. D.
例6.(2022·全国·高二课时练习)若直线与曲线有两个交点,则实数的取值范围是( )
A. B.
C. D.
例7.(2022·全国·高三专题练习)若直线y=x+b与曲线x恰有一个公共点,则b的取值范围是( )
A.﹣1<b≤1 B.﹣1≤b≤1
C.b≤﹣1 D.﹣1<b≤1或b
例8.(2022·全国·高三专题练习)若方程有两个不等的实根,则实数b的取值范围为( )
A. B. C. D.
例9.(2022·全国·高三专题练习)已知直线与圆相交于,两点,则的值为( )
A. B.16 C. D.8
例10.(2022·全国·高三专题练习)已知圆上仅有一点到直线的距离为1,则实数a的值为( ).
A.11 B. C.1 D.4
例11.(2022·全国·高三专题练习)如果圆上总存在两个点到原点的距离为,则实数的取值范围是( )
A. B.
C. D.
例12.(2022·全国·高三专题练习)若直线 与圆 相交于 两点, 且 (其中 为原点), 则 的值为( )
A. 或 B. C. 或 D.
例13.(2022·全国·高三专题练习)已知直线过点且斜率为1,若圆上恰有3个点到的距离为1,则的值为( )
A. B. C. D.
例14.(2022·全国·高二课时练习)若圆上存在四个点到直线的距离为,则实数m的取值范围是( )
A. B.
C. D.或
例15.(2022·江西·南昌大学附属中学高二期末(理))已知圆上有三个点到直线的距离等于1,则的值为( )
A. B. C. D.1
例16.(2022·四川省绵阳南山中学高二阶段练习(文))已知直线:和圆:,且圆上至少存在两点到直线的距离为1,则的取值范围是( )
A. B.
C. D.
例17.(2022·全国·高二课时练习)若圆与轴、轴均有公共点,则实数的取值范围是______.
【方法技巧与总结】
直接联立求解.
题型三:切线与切线长问题
例18.(2022·全国·高三专题练习)已知圆:,为过的圆的切线,为上任一点,过作圆:的切线,则切线长的最小值是__________.
例19.(2022·天津市武清区杨村第一中学模拟预测)由直线上的点向圆引切线(为切点),则线段的最小长度为________.
例20.(2022·云南玉溪·高二期末)已知直线经过点,且与圆相切,则的方程为( )
A. B. C. D.
例21.(2022·辽宁·大连市一0三中学模拟预测)过点作圆的切线,则切线方程为( )
A. B. C. D.或
例22.(2022·全国·高三专题练习)已知圆.求满足下列条件的切线方程.
(1)过点;
(2)过点.
例23.(2022·江苏连云港·模拟预测)直线与圆相切,则的值为( )
A. B.1 C. D.
例24.(多选题)(2022·全国·高二课时练习)过点作与圆相切的直线l,则直线l的方程为( )
A. B.
C. D.
例25.(多选题)(2022·全国·高二单元测试)设有一组圆Ck:,下列说法正确的是( )
A.这组圆的半径均为1
B.直线2x-y+2=0平分所有的圆Ck
C.存在无穷多条直线l被所有的圆Ck截得的弦长相等
D.存在一个圆Ck与x轴与y轴均相切
【方法技巧与总结】
求圆的切线方程一般有三种方法:
(1)直接法:应用常见结论,直接写出切线方程;
(2)待定系数法;
(3)定义法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.
题型四:弦长问题
例26.(2022·安徽省太和中学高三阶段练习)在平面直角坐标系中,圆被直线截得的弦长2,则实数的值为___________.
例27.(2022·河南·高三阶段练习(文))直线与圆C:相交于M,N两点,则______.
例28.(2022·全国·高二课时练习)设圆的圆心为C,直线l过,且与圆C交于A,B两点,若,则直线l的方程为___________.
例29.(2022·全国·高三专题练习)在平面直角坐标系中,已知直线与圆交于A,B两点,若钝角的面积为,则实数a的值是______.
例30.(2022·全国·模拟预测)在平面直角坐标系xOy中,过点的直线l与圆相交于M,N两点,若,则直线l的斜率为__________.
例31.(2022·全国·高二专题练习)已知圆,直线l过点且与圆O交于A,B两点,当面积最大时,直线l的方程为_________.
例32.(多选题)(2022·湖南·华容县教育科学研究室高一期末)已知动直线与圆,则下列说法正确的是( )
A.直线过定点
B.圆的圆心坐标为
C.直线与圆的相交弦的最小值为
D.直线与圆的相交弦的最大值为4
例33.(多选题)(2022·全国·高二课时练习)若直线被圆所截得的弦长为,则实数a的值为( )
A.0 B.4 C. D.
例34.(多选题)(2022·河南·范县第一中学高二阶段练习)在平面直角坐标系中,O为坐标原点,已知圆O半径为3,直线l1、l2互相垂直,垂足为M(1,2),且l1与圆O相交于A、C两点,l2与圆O交于B、D两点,则四边形ABCD面积的值可以为( )
A.11 B.12 C.13 D.14
例35.(2022·全国·高二课时练习)若直线被圆截得的弦长不大于,求实数的取值范围.
【方法技巧与总结】
弦长问题
①利用垂径定理:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
②利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
③利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:.
题型五:判断圆与圆的位置关系
例36.(2022·全国·高二课时练习)已知圆和,则两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
例37.(2022·全国·高三专题练习)已知两圆分别为圆和圆,这两圆的位置关系是( )
A.相离 B.相交 C.内切 D.外切
例38.(2022·陕西·铜川阳光中学高一期末)已知圆(,为常数)与.若圆心与圆心关于直线对称,则圆与的位置关系是( )
A.内含 B.相交 C.内切 D.相离
【方法技巧与总结】
已知两圆半径分别为,两圆的圆心距为,则:
(1)两圆外离;
(2)两圆外切;
(3)两圆相交;
(4)两圆内切;
(5)两圆内含;
题型六:由圆的位置关系确定参数
例39.(2022·云南省下关第一中学高三开学考试)若圆上总存在两个点到点的距离为2,则实数a的取值范围是( )
A. B.
C. D.
例40.(2022·湖北·荆门市龙泉中学二模)若点到直线的距离分别为1和4,则这样的直线共有( )条
A.4 B.3 C.2 D.1
例41.(2022·浙江·乐清市知临中学高二期中)已知,两点到直线的距离分别是2和3,则满足条件的直线共有( )条.
A.1 B.2 C.3 D.4
例42.(2022·全国·高三专题练习)已知圆和两点,,.若圆上存在点,使得,则的最小值为( )
A.7 B.6 C.5 D.4
例43.(2022·山东聊城·二模)已知点在圆:上,点,,满足的点的个数为( )
A.3 B.2 C.1 D.0
例44.(2022·全国·高三专题练习)若圆上存在点P,且点P关于直线y=x的对称点Q在圆上,则r的取值范围是( )
A. B. C. D.
【方法技巧与总结】
利用几何法判定两圆的位置关系比用代数法(即解两圆方程联立方程组的方法)要简捷些,但需要注意的是,我们这里所说的几何法仍然是在解析几何前提下的几何法,即利用圆的方程及两点间距离公式求出两圆圆心距d和两圆的半径R和r,再根据d与、d与的大小关系来判定即可.
题型七:公共弦与切点弦问题
例45.(2022·广东·高三阶段练习)已知:,直线:,为直线上的动点,过点作的切线,,切点为,,当四边形的面积取最小值时,直线AB的方程为 ____.
例46.(2022·江苏·高二专题练习)已知圆的方程为,点是直线上的一个动点,过点作圆的两条切线、,、为切点,则四边形的面积的最小值为______
例47.(2022·云南·昆明一中高三开学考试)已知圆和圆交于两点,则直线的方程是___________.
例48.(2022·全国·高三专题练习)圆与圆的公共弦长为______.
例49.(2022·全国·高三专题练习)已知圆:,点是直线上的动点,过作圆的两条切线,切点分别为,,则的最小值为( )
A. B. C. D.
例50.(2022·全国·高三专题练习)已知圆,点M为直线上一个动点,过点M作圆C的两条切线,切点分别为A,B,则四边形周长的最小值为( )
A.8 B. C. D.
例51.(2022·全国·高二课时练习)已知点P为直线上的动点,过点P作圆的两条切线,切点分别为A B,则直线必过定点( )
A. B. C. D.
例52.(2022·安徽·屯溪一中高二期中)已知直线是圆的对称轴.过点作圆的两条切线,切点分别为、,则直线的方程为( )
A. B. C. D.
例53.(2022·四川省绵阳第一中学高二期中)过点作圆C:的两条切线,切点分别为A,B,则直线AB的方程为( )
A. B. C. D.
例54.(2022·江苏常州·一模)过圆:外一点作圆的切线,切点分别为、,则( )
A.2 B. C. D.3
例55.(2022·江苏·高二专题练习)已知圆M:,直线l:,P为直线l上的动点,过P点作圆M的切线PA、PB,切点为A、B,当最小时,直线AB的方程为( )
A. B.
C. D.
例56.(多选题)(2022·全国·高二课时练习)圆和圆的交点为A,B,则有( )
A.公共弦AB所在直线的方程为
B.公共弦AB所在直线的方程为
C.公共弦AB的长为
D.P为圆上一动点,则P到直线AB距离的最大值为
例57.(2022·广东·汕头市潮阳区棉城中学高二期中)过直线上任意点作圆的两条切线,切点分别为,当切线长最小时,切线长为_________;同时 的面积为_______.
例58.(2022·浙江绍兴·模拟预测)已知圆C的方程为,则圆心C的坐标为___________,圆C与圆D:的公共弦所在直线方程为___________.
【方法技巧与总结】
(1)圆的切线方程的求法
①点在圆上,
法一:利用切线的斜率与圆心和该点连线的斜率的乘积等于,即.
法二:圆心到直线的距离等于半径.
②点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
注意:因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
(2)常见圆的切线方程
过圆上一点的切线方程是;
过圆上一点的切线方程是.
过圆外一点作圆的两条切线,则两切点所在直线方程为
过曲线上,做曲线的切线,只需把替换为,替换为,替换为,替换为即可,因此可得到上面的结论.
(3)两圆的公共弦方程为两圆方程相减可得.
题型八:公切线问题
例59.(2022·广东·中山一中高三阶段练习)已知圆.若圆与圆有三条公切线,则的值为___________.
例60.(2022·广东广州·高二期末)写出与圆和圆都相切的一条切线方程___________.
例61.(多选题)(2022·全国·高二课时练习)已知圆,圆,则下列是M,N两圆公切线的直线方程为( )
A.y=0 B.3x-4y=0 C. D.
例62.(2022·全国·高二专题练习)若直线与圆,圆都相切,切点分别为、,则( )
A. B. C. D.
例63.(2022·全国·高二单元测试)已知点M,N分别在圆与圆上,则的最大值为( )
A. B.17 C. D.15
例64.(多选题)(2022·全国·高二课时练习)若直线与圆相切,则直线与圆的位置关系可能是( )
A.相交 B.相切 C.相离 D.不确定
例65.(2022·全国·高三专题练习)在平面直角坐标系中,圆:与圆:,则两圆的公切线的条数是( )
A.4条 B.3条 C.2条 D.1条
例66.(2022·全国·高三专题练习)已知圆,圆,则同时与圆和圆相切的直线有( )
A.4条 B.2条 C.1条 D.0条
例67.(2022·全国·高二课时练习)求圆与圆的公切线所在直线的方程.
例68.(2022·全国·高二专题练习)求圆与圆的内公切线所在直线方程及内公切线的长.
【方法技巧与总结】
利用几何法进行转化.
题型九:圆中范围与最值问题
例69.(2022·江苏·高二专题练习)已知 ,且动点满足,则取得最小值时,点的坐标是___________.
例70.(2022·全国·模拟预测)已知直线与圆交于不同的两点,,点,则的最大值为______.
例71.(2022·重庆一中高一期末)直线分别与x轴 y轴相交于A B两点,点P在圆上运动,则面积的最小值为___________.
例72.(2022·全国·高二课时练习)若点M为圆上任意一点,直线过定点P,则的最大值为______.
例73.(2022·上海市控江中学高二期末)已知点在圆上运动,则的最大值为( )
A. B. C. D.
例74.(2022·河南·修武一中高二开学考试(理))已知直线与圆交于两点,过分别作的垂线与轴交于两点,则当最小时,( )
A.4 B. C.8 D.
例75.(2022·广东·佛山一中高二期中)已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形面积为( )
A. B. C. D.
例76.(2022·全国·高三专题练习)当圆的圆心到直线的距离最大时,( )
A. B. C. D.
例77.(2022·全国·高二专题练习)已知圆上的点到直线的距离等于,那么的值不可以是( )
A. B. C. D.
例78.(多选题)(2022·江苏·高二专题练习)圆C方程:,P为圆上的动点,则下列说法错误的是( )
A.的最大值为
B.P点到A点距离的最小值为
C.的最大值为
D.圆C的内接正三角形的面积为
例79.(2022·全国·高二课时练习)已知圆.
(1)直线过点,且与圆C相切,求直线的方程;
(2)设直线与圆C相交于M,N两点,点P为圆C上的一动点,求的面积S的最大值.
【方法技巧与总结】
涉及与圆有关的最值,可借助图形性质,利用数形结合求解.一般地:
(1)形如的最值问题,可转化为动直线斜率的最值问题.
(2)形如的最值问题,可转化为动直线截距的最值问题.
(3)形如的最值问题,可转化为曲线上的点到点(a,b)的距离平方的最值问题
题型十:圆系问题
例80.(2022·全国·高二专题练习)求经过圆与直线的交点且在轴上的弦长为的圆的方程.
例81.(2022·江苏·高二专题练习)已知圆:与:相交于A、B两点.
(1)求公共弦AB所在的直线方程;
(2)求圆心在直线y=-x上,且经过A、B两点的圆的方程;
(3)求经过A、B两点且面积最小的圆的方程.
例82.过圆与的交点,且圆心在直线上的圆的方程是_______.
例83.已知圆与圆相交于A、B两点.
(1)求公共弦AB所在直线方程;
(2)求过两圆交点A、B,且过原点的圆的方程.
【方法技巧与总结】
圆系方程:若圆与圆相交于A,B两点,则过A,B两点的圆系方程为:
简记为:,不含
当时,该圆系退化为公共弦所在直线(根轴)
注意:与圆C共根轴l的圆系
【同步练习】
一、单选题
1.设圆,圆,则圆,的公切线有( )
A.1条 B.2条 C.3条 D.4条
2.求与直线平行且将圆的周长平分的直线方程为( )
A. B.
C. D.
3.直线绕原点按逆时针方向旋转后所得的直线l与圆的位置关系是( )
A.直线l过圆心 B.直线l与圆相交,但不过圆心
C.直线l与圆相切 D.直线l与圆无公共点
4.设是圆上的动点,是圆的切线,且,则点到点距离的最小值为( )
A.4 B.5 C.6 D.15
5.已知直线l:与圆O:相交于不同的两点A,B,若∠AOB为锐角,则m的取值范围为( )
A. B.
C. D.
6.若点C到的距离之比为,则点C到直线的距离的最小值为( )
A. B. C. D.
7.古希腊数学家阿波罗尼斯(约前262—前190年)的著作《圆锥曲线论》是古代光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数且的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.已知,,圆上有且仅有一个点P满足,则r的取值为( )
A.1 B.5 C.1或5 D.不存在
8.从空中某个角度俯视北京冬奥会主体育场“鸟巢”顶棚所得的局部示意图如图,在平面直角坐标系中,下列直线系方程(其中为参数,)能形成这种效果的是( )
A. B.
C. D.
二、多选题
9.已知圆与圆有四条公切线,则实数a的取值可能是( )
A.-4 B.-2 C. D.3
10.已知圆C:,则下列四个命题表述正确的是( )
A.圆C上有且仅有3个点到直线1:的距离都等于1
B.过点作圆C的两条切线,切点分别为M,N,直线MN的方程为
C.一条直线与圆C交于不同的两点P,Q,且有,则∠PCQ的最大值为
D.若圆C与E:相外切,则
11.已知M为圆C:上的动点,P为直线l:上的动点,则下列结论正确的是( )
A.直线l与圆C相切 B.直线l与圆C相离
C.|PM|的最大值为 D.|PM|的最小值为
12.若实数x,y满足,则下列说法正确的是( )
A.x的最小值是4
B.x的最大值是20
C.若关于y的方程有一解,则x的取值范围为
D.若关于y的方程有两解,则x的取值范围为
三、填空题
13.大约在2000多年前,我国的墨子给出了圆的概念“一中同长也”,意思是说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下定义要早100多年.已知直角坐标平面内有一点和一动点满足,若过点的直线将动点的轨迹分成两段弧,当劣弧所对的圆心角最小时,直线的斜率__________.
14.规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置,球是指该球的球心点.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为1的圆,且母球与目标球有公共点时,目标球就开始运动,在桌面上建立平面直角坐标系,如图,设母球的位置为(0,0),目标球的位置为,要使目标球向处运动,则母球的球心运动的直线方程为______.
15.直线与半圆有两个交点,则的值是____.
16.设直线系,对于下列四个命题:
①M中所有直线均经过一个定点;
②存在定点P不在M中的任一条直线上;
③对于任意整数,存在正n边形,使其所有边均在M中的直线上;
④M中的直线所能围成的正三角形面积都相等.
其中真命题的序号是_________(写出所有真命题的序号)
四、解答题
17.从①与直线4x-3y+5=0垂直,②过点(5,-5),③与直线3x+4y+2=0平行这三个条件中任选一个,补充在下面的问题中,并加以解答.
问题:已知直线l过点,且______.
(1)求直线l的一般式方程;
(2)若直线l与圆相交于点P,Q,求弦PQ的长.
注:如果选择多个条件分别解答,按第一个解答计分.
18.在①,②最小,③过A,B两点分别作圆C的切线,切线交于点P(2,0)这三个条件中任选一个,补充在下面问题中,并求解.
在平面直角坐标系中,已知圆,直线l过定点M(1,1).设直线l与圆C交于A,B两点,当______时,求直线l的方程.
19.已知圆,平面上一动点P满足:且,.
(1)求动点P的轨迹方程;
(2)过点N的直线l(斜率为正)交圆G于A C两点,交P的轨迹于B D两点(A B在第一象限),若,求直线l的方程.
20.已知直线过定点,且与圆交于、两点.
(1)求直线的斜率的取值范围.
(2)若为坐标原点,直线、的斜率分别为、,试问是否为定值?若是,求出该定值;若不是,请说明理由.
21.在平面直角坐标系中,光线过点,经轴反射后与圆:有交点
(1)当反射后光线经过圆心,求光线的方程;
(2)当反射后光线与圆相切,求光线的方程.
22.如图,在平面直角坐标系上,已知圆的直径,定直线到圆心的距离为,且直线垂直于直线,点是圆上异于、的任意一点,直线、分别交与、两点.
(1)求过点且与圆相切的直线方程;
(2)若,求以为直径的圆方程;
(3)当点变化时,以为直径的圆是否过圆内的一定点,若过定点,请求出定点;若不过定点,请说明理由
2.5 直线与圆、圆与圆的位置关系
【知识点梳理】
知识点一:直线与圆的位置关系
1.直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2.直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
知识点诠释:
(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.
(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.
(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.
知识点二:圆的切线方程的求法
1.点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率
的乘积等于,即.
法二:圆心到直线的距离等于半径.
2.点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
知识点诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是
.
知识点三:求直线被圆截得的弦长的方法
1.应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
2.利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
知识点四:圆与圆的位置关系
1.圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
2.圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
知识点诠释:
判定圆与圆的位置关系主要是利用几何法,通过比较两圆的圆心距和两圆的半径的关系来确定,这种方法运算量小.也可利用代数法,但是利用代数法解决时,一是运算量大,二是方程组仅有一解或无解时,两圆的位置关系不明确,还要比较两圆的圆心距和两圆半径的关系来确定.因此,在处理圆与圆的位置关系时,一般不用代数法.
3.两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
4.两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
【题型归纳目录】
题型一:不含参数(含参数)的直线与圆的位置关系
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
题型三:切线与切线长问题
题型四:弦长问题
题型五:判断圆与圆的位置关系
题型六:由圆的位置关系确定参数
题型七:公共弦与切点弦问题
题型八:公切线问题
题型九:圆中范围与最值问题
题型十:圆系问题
【典型例题】
题型一:不含参数(含参数)的直线与圆的位置关系
例1.(2022·全国·高二课时练习)直线和圆的位置关系为( )
A.相交 B.相切或相交 C.相离 D.相切
【答案】A
【解析】由,得,
所以圆心为,半径为.
因为圆心到直线的距离为
,
所以直线和圆相交.
故选:A
例2.(2022·西藏·林芝市第二高级中学高一期末)圆x2+y2-2x+4y=0与直线2x+y+1=0的位置关系为( )
A.相离 B.相切 C.相交 D.以上都有可能
【答案】C
【解析】圆x2+y2-2x+4y=0的圆心坐标为,半径
圆心到直线2x+y+1=0的距离
由,可得圆与直线的位置关系为相交.
故选:C
例3.(2022·全国·高三专题练习)直线与圆的位置关系为( )
A.相切 B.相交
C.相离 D.由的取值确定
【答案】A
【解析】因为圆心到直线的距离,即为圆的半径,所以可知直线与圆相切.
故选:A.
例4.(2022·全国·高二专题练习)圆与直线的位置关系为( )
A.相切 B.相离 C.相交 D.无法确定
【答案】C
【解析】直线可化为,所以恒过定点.
把代入,有:,
所以在圆内,所以圆与直线的位置关系为相交.
故选:C
【方法技巧与总结】
直线与圆的位置关系判断方法
法一抓住直线与圆的位置关系的代数特征,从而转化为对方程的解的研究,这是研究直线与曲线的位置关系的基本方法;法二抓住直线与圆的位置关系的几何特征,从而转化为研究圆心到直线的距离,抓住几何特征对于研究圆的问题特别有效;法三通过判定直线过圆内一定点,从而使问题获证.由上述三种解法可知,解题的切入点不同,解法就有优劣之分.因此,在解题时,审题要慢,要仔细地分析题意,透彻地理解题意,挖掘其中的隐含条件,从而找到解决问题的捷径.
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
例5.(2022·福建省福州第二中学高二期末)已知直线平分圆:,则的最大值为( )
A. B. C. D.
【答案】B
【解析】圆:,圆心,
直线平分圆:,
直线过圆心,即,
,
当且仅当,即,的最大值为.
故选:B
例6.(2022·全国·高二课时练习)若直线与曲线有两个交点,则实数的取值范围是( )
A. B.
C. D.
【答案】C
【解析】由题意,直线的方程可化为,所以直线恒过定点,,可化为其表示以为圆心,半径为2的圆的一部分,如图.
当与该曲线相切时,点到直线的距离,解得.
设,则.由图可得,若要使直线与曲线有两个交点,则.
故选:C.
例7.(2022·全国·高三专题练习)若直线y=x+b与曲线x恰有一个公共点,则b的取值范围是( )
A.﹣1<b≤1 B.﹣1≤b≤1
C.b≤﹣1 D.﹣1<b≤1或b
【答案】D
【解析】曲线x即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图所示.
当直线y=x+b经过点A(0,1)时,求得b=1,
当直线y=x+b经过点B(1,0)时,求得b=﹣1,
当直线和半圆相切于点D时,由圆心O到直线y=x+b的距离等于半径,
可得1,求得b,或b(舍去).
故当直线y=x+b与曲线x恰有一个公共点时b的取值范围是﹣1<b≤1或b,
故选:D.
例8.(2022·全国·高三专题练习)若方程有两个不等的实根,则实数b的取值范围为( )
A. B. C. D.
【答案】B
【解析】由得,
所以直线与半圆有个公共点,
作出直线与半圆的图形,如图:
当直线经过点时,,
当直线与圆相切时,,解得或(舍),
由图可知,当直线与曲线有个公共点时,,
故选:B.
例9.(2022·全国·高三专题练习)已知直线与圆相交于,两点,则的值为( )
A. B.16 C. D.8
【答案】C
【解析】因为直线与圆相交于A,B两点,
所以,解得:.
所以.
故选:C.
例10.(2022·全国·高三专题练习)已知圆上仅有一点到直线的距离为1,则实数a的值为( ).
A.11 B. C.1 D.4
【答案】C
【解析】圆的标准方程是,圆心为,半径为,
圆心到直线的距离.
因为圆上仅有一点到直线的距离为1,
所以圆的半径,解得.
故选:C.
例11.(2022·全国·高三专题练习)如果圆上总存在两个点到原点的距离为,则实数的取值范围是( )
A. B.
C. D.
【答案】D
【解析】问题可转化为圆和圆相交,
两圆圆心距,
由得,
解得,即.
故选:D
例12.(2022·全国·高三专题练习)若直线 与圆 相交于 两点, 且 (其中 为原点), 则 的值为( )
A. 或 B. C. 或 D.
【答案】A
【解析】由可知,圆心到直线的距离为,根据点到直线的距离公式可得
故选:A
例13.(2022·全国·高三专题练习)已知直线过点且斜率为1,若圆上恰有3个点到的距离为1,则的值为( )
A. B. C. D.
【答案】D
【解析】直线过点且斜率为1,
设,
圆上恰有3个点到的距离为1,
圆心到直线的距离等于半径减去1,
圆心到直线的距离为,解得.
故选:D.
例14.(2022·全国·高二课时练习)若圆上存在四个点到直线的距离为,则实数m的取值范围是( )
A. B.
C. D.或
【答案】C
【解析】由题设,且半径,又圆上存在四个点到的距离为,
∴到的距离,可得.
故选:C
例15.(2022·江西·南昌大学附属中学高二期末(理))已知圆上有三个点到直线的距离等于1,则的值为( )
A. B. C. D.1
【答案】A
【解析】由圆可得圆心,半径,
因为圆上有三个点到直线的距离等于1,
所以圆心到直线的距离,
可得:,
故选:A.
例16.(2022·四川省绵阳南山中学高二阶段练习(文))已知直线:和圆:,且圆上至少存在两点到直线的距离为1,则的取值范围是( )
A. B.
C. D.
【答案】A
【解析】圆的方程为:,则圆心为,要使圆上至少存在两点到直线的距离为1,则当圆心到直线的距离必须小于3,即,解得.
故选:A
例17.(2022·全国·高二课时练习)若圆与轴、轴均有公共点,则实数的取值范围是______.
【答案】
【解析】圆的标准方程为,圆心坐标为,半径长为,
且该圆与轴、轴均有公共点,所以,,解得.
因此,实数的取值范围是.
故答案为:.
【方法技巧与总结】
直接联立求解.
题型三:切线与切线长问题
例18.(2022·全国·高三专题练习)已知圆:,为过的圆的切线,为上任一点,过作圆:的切线,则切线长的最小值是__________.
【答案】
【解析】由题,直线的斜率为,故直线的斜率为,故的方程为,即.又到的距离,故切线长的最小值是
故答案为:
例19.(2022·天津市武清区杨村第一中学模拟预测)由直线上的点向圆引切线(为切点),则线段的最小长度为________.
【答案】
【解析】圆的圆心,半径,点到直线的距离,
于是得,当且仅当垂直于直线时取“=“,
所以线段的最小长度为.
故答案为:
例20.(2022·云南玉溪·高二期末)已知直线经过点,且与圆相切,则的方程为( )
A. B. C. D.
【答案】A
【解析】直线经过点,且与圆相切,则,
故直线的方程为,即.
故选:A.
例21.(2022·辽宁·大连市一0三中学模拟预测)过点作圆的切线,则切线方程为( )
A. B. C. D.或
【答案】C
【解析】由圆心为,半径为,
斜率存在时,设切线为,则,可得,
所以,即,
斜率不存在时,显然不与圆相切;
综上,切线方程为.
故选:C
例22.(2022·全国·高三专题练习)已知圆.求满足下列条件的切线方程.
(1)过点;
(2)过点.
【解析】(1)因为圆的圆心为,半径为,点在圆上,
所以过点的切线斜率存在,且其与直线垂直,
因为,所以,所求切线的斜率为,
所以,所求切线方程为,即:.
(2)因为圆的圆心为,半径为,
所以,当过点的切线斜率不存在时,其方程为,满足题意;
当切线斜率存在时,设斜率为,则其方程为,即,
所以,圆心到切线的距离为,解得,
所以,切线方程为,即:.
综上,所求切线方程为或
例23.(2022·江苏连云港·模拟预测)直线与圆相切,则的值为( )
A. B.1 C. D.
【答案】C
【解析】因为直线与圆相切,
所以由圆心到直线的距离等于半径得:,即,解得:.
故选:C
例24.(多选题)(2022·全国·高二课时练习)过点作与圆相切的直线l,则直线l的方程为( )
A. B.
C. D.
【答案】BC
【解析】圆,即,则圆心为,半径为1,易知点在圆外,
显然是其中一条切线.
当切线斜率存在时,设切线方程为,则,解得,
所以切线方程为.综上,切线方程为或.
故选:BC.
例25.(多选题)(2022·全国·高二单元测试)设有一组圆Ck:,下列说法正确的是( )
A.这组圆的半径均为1
B.直线2x-y+2=0平分所有的圆Ck
C.存在无穷多条直线l被所有的圆Ck截得的弦长相等
D.存在一个圆Ck与x轴与y轴均相切
【答案】ABC
【解析】对于选项A:由圆Ck的方程可知,这组圆的半径均为1,故A正确;
对于选项B:圆Ck的圆心坐标为,因为2(k-1)-2k+2=0,所以直线2x-y+2=0过圆Ck的圆心,故B正确;
对于选项C:由B知,直线2x-y+2=0平分所有的圆Ck,所以存在无数条与直线2x-y+2=0平行或重合的直线(与直线2x-y+2=0的距离小于1)被所有的圆Ck截得的弦长相等,故C正确;
对于选项D:若圆Ck与x轴和y轴均相切,则,无解,故D错误.
故选:ABC.
【方法技巧与总结】
求圆的切线方程一般有三种方法:
(1)直接法:应用常见结论,直接写出切线方程;
(2)待定系数法;
(3)定义法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.
题型四:弦长问题
例26.(2022·安徽省太和中学高三阶段练习)在平面直角坐标系中,圆被直线截得的弦长2,则实数的值为___________.
【答案】
【解析】因为,所以圆心到直线的距离,所以,解得.
故答案为:
例27.(2022·河南·高三阶段练习(文))直线与圆C:相交于M,N两点,则______.
【答案】4
【解析】圆C:,其圆心坐标为,半径为3.
圆心到直线2x-y+1=0的距离,
则.
故答案为:4.
例28.(2022·全国·高二课时练习)设圆的圆心为C,直线l过,且与圆C交于A,B两点,若,则直线l的方程为___________.
【答案】或
【解析】当直线l的斜率不存在时,直线l的方程为,
由,得或,
此时,符合题意.
当直线l的斜率存在时,设直线,
因为圆的圆心,半径,
所以圆心C到直线l的距离.
因为,所以,解得,
所以直线l的方程为,即.
综上,直线l的方程为或.
故答案为:或
例29.(2022·全国·高三专题练习)在平面直角坐标系中,已知直线与圆交于A,B两点,若钝角的面积为,则实数a的值是______.
【答案】
【解析】由圆,即,
可得圆心坐标为,半径为,
因为钝角的面积为,可得,
解得,因为,所以,
可得,
设圆心到直线的距离为,又由圆的弦长公式,可得,解得,
根据点到直线的距离公式,解得.
故答案为:.
例30.(2022·全国·模拟预测)在平面直角坐标系xOy中,过点的直线l与圆相交于M,N两点,若,则直线l的斜率为__________.
【答案】
【解析】由题意得,直线的斜率存在,设,,直线MN的方程为,与联立,得,,得,,.因为,所以,则,于是,(由点A及C在y轴上可判断出,同号)
所以,两式消去,得,满足,所以.
故答案为:
例31.(2022·全国·高二专题练习)已知圆,直线l过点且与圆O交于A,B两点,当面积最大时,直线l的方程为_________.
【答案】
【解析】当直线l的斜率不存在时,直线l的方程为,
则由,得,所以
,
当直线l的斜率存在时,设直线l的方程为
原点到直线l的距离为:
当且仅当,即时取得等号.
由,解得
由
故直线l的方程为:,即
故答案为:
例32.(多选题)(2022·湖南·华容县教育科学研究室高一期末)已知动直线与圆,则下列说法正确的是( )
A.直线过定点
B.圆的圆心坐标为
C.直线与圆的相交弦的最小值为
D.直线与圆的相交弦的最大值为4
【答案】ACD
【解析】对于A,直线,即,
令,得,即直线过定点,故A正确;
对于B,圆,即,圆心坐标为,故B错误;
对于C,因为,所以直线所过定点在圆的内部,不妨设直线过定点为,
当直线与圆的相交弦的最小时,与相交弦垂直,
又因为,所以相交弦的最小为,故C正确;
对于D,直线与圆的相交弦的最大值为圆直径4,故D正确.
故选:ACD
例33.(多选题)(2022·全国·高二课时练习)若直线被圆所截得的弦长为,则实数a的值为( )
A.0 B.4 C. D.
【答案】AB
【解析】由圆的方程可知圆心坐标为,半径.
又直线被圆截得的弦长为,
所以圆心到直线的距离.
又,
所以,解得或.
故选:AB
例34.(多选题)(2022·河南·范县第一中学高二阶段练习)在平面直角坐标系中,O为坐标原点,已知圆O半径为3,直线l1、l2互相垂直,垂足为M(1,2),且l1与圆O相交于A、C两点,l2与圆O交于B、D两点,则四边形ABCD面积的值可以为( )
A.11 B.12 C.13 D.14
【答案】BC
【解析】如图,作于点,于点,
则,,则.
因为,所以,即,所以,故当时,有最大值26,此时,当或时,有最小值24,此时,所以四边形ABCD面积的范围为.
故选:BC
例35.(2022·全国·高二课时练习)若直线被圆截得的弦长不大于,求实数的取值范围.
【解析】圆的圆半径为,
设直线被圆截得的弦长为,圆心到直线的距离,
由题意,得,即,所以.
又,所以,所以或,
结合,可知或.
综上,实数的取值范围为.
【方法技巧与总结】
弦长问题
①利用垂径定理:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
②利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
③利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:.
题型五:判断圆与圆的位置关系
例36.(2022·全国·高二课时练习)已知圆和,则两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
【答案】C
【解析】由题意,知圆的圆心,半径.
圆的方程可化为,则其圆心,半径.
因为两圆的圆心距,故两圆外切.
故选:C.
例37.(2022·全国·高三专题练习)已知两圆分别为圆和圆,这两圆的位置关系是( )
A.相离 B.相交 C.内切 D.外切
【答案】B
【解析】由题意得,圆圆心,半径为7;圆,圆心,半径为4,
两圆心之间的距离为,因为,故这两圆的位置关系是相交.
故选:B.
例38.(2022·陕西·铜川阳光中学高一期末)已知圆(,为常数)与.若圆心与圆心关于直线对称,则圆与的位置关系是( )
A.内含 B.相交 C.内切 D.相离
【答案】B
【解析】,,半径为,
关于直线的对称点为,即,所以,圆半径为,
,又,
所以两圆相交.
故选:B.
【方法技巧与总结】
已知两圆半径分别为,两圆的圆心距为,则:
(1)两圆外离;
(2)两圆外切;
(3)两圆相交;
(4)两圆内切;
(5)两圆内含;
题型六:由圆的位置关系确定参数
例39.(2022·云南省下关第一中学高三开学考试)若圆上总存在两个点到点的距离为2,则实数a的取值范围是( )
A. B.
C. D.
【答案】A
【解析】到点的距离为2的点在圆上,
所以问题等价于圆上总存在两个点也在圆上,
即两圆相交,故,
解得或,
所以实数a的取值范围为,
故选:A.
例40.(2022·湖北·荆门市龙泉中学二模)若点到直线的距离分别为1和4,则这样的直线共有( )条
A.4 B.3 C.2 D.1
【答案】C
【解析】到点距离为1的直线,可看作以为圆心1为半径的圆的切线,
同理到点距离为的直线,可看作以为圆心为半径的圆的切线,
故所求直线为两圆的公切线,
又,所以,故两圆相交,公切线有条,
故选:C.
例41.(2022·浙江·乐清市知临中学高二期中)已知,两点到直线的距离分别是2和3,则满足条件的直线共有( )条.
A.1 B.2 C.3 D.4
【答案】C
【解析】解析:分别以,为圆心,半径分别是2和3画圆,,两圆位置关系是外切,公切线有三条,
故选:C.
【点晴】此题的关键是发现直线和两点之间的关系,充分体现了数形结合思想的强大之处.
例42.(2022·全国·高三专题练习)已知圆和两点,,.若圆上存在点,使得,则的最小值为( )
A.7 B.6 C.5 D.4
【答案】D
【解析】
,点的轨迹是以为直径的圆,
又点在圆上,故点是圆与圆的交点,
因此可得两圆的位置关系是相切或相交,即,
解得:.
的最小值为4.
故选:D.
例43.(2022·山东聊城·二模)已知点在圆:上,点,,满足的点的个数为( )
A.3 B.2 C.1 D.0
【答案】B
【解析】设点,则,
且,由,得
,
即,
故点P的轨迹为一个圆心为、半径为的圆,
则两圆的圆心距为,半径和为,半径差为,
有,所以两圆相交,满足这样的点P有2个.
故选:B.
例44.(2022·全国·高三专题练习)若圆上存在点P,且点P关于直线y=x的对称点Q在圆上,则r的取值范围是( )
A. B. C. D.
【答案】A
【解析】根据题意,圆的圆心坐标为(0,1),半径为r,其关于直线y=x的对称圆的方程为,根据题意,圆与圆有交点,既可以是外切,也可以是相交,也可以是内切.
又圆,所以圆与圆的圆心距为,所以只需,解得.故B,C,D错误.
故选:A.
【方法技巧与总结】
利用几何法判定两圆的位置关系比用代数法(即解两圆方程联立方程组的方法)要简捷些,但需要注意的是,我们这里所说的几何法仍然是在解析几何前提下的几何法,即利用圆的方程及两点间距离公式求出两圆圆心距d和两圆的半径R和r,再根据d与、d与的大小关系来判定即可.
题型七:公共弦与切点弦问题
例45.(2022·广东·高三阶段练习)已知:,直线:,为直线上的动点,过点作的切线,,切点为,,当四边形的面积取最小值时,直线AB的方程为 ____.
【答案】
【解析】:的标准方程为,
则圆心,半径.
因为四边形的面积,
要使四边形面积最小,则需最小,此时与直线垂直,
直线的方程为,即,
联立,解得.则,
则以为直径的圆的方程为,
与的方程作差可得直线的方程为.
故答案为:.
例46.(2022·江苏·高二专题练习)已知圆的方程为,点是直线上的一个动点,过点作圆的两条切线、,、为切点,则四边形的面积的最小值为______
【答案】
【解析】由圆,得到圆心,半径
由题意可得:,,,
,
在中,由勾股定理可得:,
当最小时,最小,此时所求的面积也最小,
点是直线上的动点,
当时,有最小值,此时,
所求四边形的面积的最小值为;
故答案为:
例47.(2022·云南·昆明一中高三开学考试)已知圆和圆交于两点,则直线的方程是___________.
【答案】
【解析】由两圆相交,则交线的方程由两圆方程相减得到,
所以直线的方程是.
故答案为:
例48.(2022·全国·高三专题练习)圆与圆的公共弦长为______.
【答案】
【解析】设圆:与圆:交于,两点
把两圆方程相减,化简得
即:
圆心到直线的距离,又
而,所以
故答案为:
例49.(2022·全国·高三专题练习)已知圆:,点是直线上的动点,过作圆的两条切线,切点分别为,,则的最小值为( )
A. B. C. D.
【答案】B
【解析】圆:化为标准方程:,其圆心,半径.
过点P引圆C的两条切线,切点分别为点A、B,如图:
在△PAC中,有,即,变形可得:.
设,则.
所以当的值即x最小时,的值最大,此时最小.
而的最小值为点C到直线的距离,即,
所以.
故选:B
例50.(2022·全国·高三专题练习)已知圆,点M为直线上一个动点,过点M作圆C的两条切线,切点分别为A,B,则四边形周长的最小值为( )
A.8 B. C. D.
【答案】A
【解析】圆的圆心坐标为,半径为,
因为过点M作圆C的两条切线,切点分别为A,B,
所以有,,
因此有,
要想四边形周长最小,只需最小,即当时,
此时,此时,
即最小值为,
故选:A
例51.(2022·全国·高二课时练习)已知点P为直线上的动点,过点P作圆的两条切线,切点分别为A B,则直线必过定点( )
A. B. C. D.
【答案】A
【解析】设,
圆的圆心为,一般方程为①,
线段中点坐标为,
,
所以以线段为直径的圆的方程为,
整理得②,
①-②并化简得,
即,
.
所以定点坐标为.
故选:A
例52.(2022·安徽·屯溪一中高二期中)已知直线是圆的对称轴.过点作圆的两条切线,切点分别为、,则直线的方程为( )
A. B. C. D.
【答案】A
【解析】根据题意,圆C的标准方程为,即圆心为 C(2,1),半径为2.
点(2,1)在直线上,即
点A的坐标为(-4,-1)
过点A作圆C的切线所得切线长为
以点A为圆心,6为半径的圆A的方程为
圆A与圆C的方程作差得,即直线BD的方程为
故选:A.
例53.(2022·四川省绵阳第一中学高二期中)过点作圆C:的两条切线,切点分别为A,B,则直线AB的方程为( )
A. B. C. D.
【答案】A
【解析】,即,圆心为,半径.
当斜率不存在时,直线与圆相切,切点为;
当斜率为0时,直线与圆相切,切点为.
故直线方程为斜率,直线方程为,即.
故选:A.
例54.(2022·江苏常州·一模)过圆:外一点作圆的切线,切点分别为、,则( )
A.2 B. C. D.3
【答案】C
【解析】如图,结合题意绘出图像:
因为圆:,直线、是圆的切线,
所以,,,,
因为,所以,,
根据圆的对称性易知,则,
解得,,
故选:C.
例55.(2022·江苏·高二专题练习)已知圆M:,直线l:,P为直线l上的动点,过P点作圆M的切线PA、PB,切点为A、B,当最小时,直线AB的方程为( )
A. B.
C. D.
【答案】A
【解析】因为圆,即为,
所以圆心,半径.
.
要使最小,则需最小,此时PM与直线l垂直.
直线PM的方程为,即,
联立,解得,即.
则以PM为直径的圆O的方程为.
直线AB为圆M与圆O公共弦所在直线,
联立
相减可得直线AB的方程为.
故选:A.
例56.(多选题)(2022·全国·高二课时练习)圆和圆的交点为A,B,则有( )
A.公共弦AB所在直线的方程为
B.公共弦AB所在直线的方程为
C.公共弦AB的长为
D.P为圆上一动点,则P到直线AB距离的最大值为
【答案】AD
【解析】由与作差可得,
即公共弦AB所在直线的方程为,故A正确,B错误;
对于C,圆心到直线的距离为,圆的半径,
所以,故C错误;
对于D,点P为圆上一动点,则点P到直线AB距离的最大值为,故D正确.
故选:AD.
例57.(2022·广东·汕头市潮阳区棉城中学高二期中)过直线上任意点作圆的两条切线,切点分别为,当切线长最小时,切线长为_________;同时 的面积为_______.
【答案】 1
【解析】依据题意,作出图形,如下图:
因为直线过点且与圆相切于点A,
所以,所以,
要使得最小,则要最小,
由题可得:的最小值就是点到直线的距离.
此时,,所以
由切线的对称性可得:
所以的面积为,
故答案为:1;.
例58.(2022·浙江绍兴·模拟预测)已知圆C的方程为,则圆心C的坐标为___________,圆C与圆D:的公共弦所在直线方程为___________.
【答案】
【解析】因为圆C的方程为,即,
故圆心C的坐标为;
由于圆D:,两圆方程相减可得,
即公共弦所在直线方程为,
故答案为:,.
【方法技巧与总结】
(1)圆的切线方程的求法
①点在圆上,
法一:利用切线的斜率与圆心和该点连线的斜率的乘积等于,即.
法二:圆心到直线的距离等于半径.
②点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
注意:因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
(2)常见圆的切线方程
过圆上一点的切线方程是;
过圆上一点的切线方程是.
过圆外一点作圆的两条切线,则两切点所在直线方程为
过曲线上,做曲线的切线,只需把替换为,替换为,替换为,替换为即可,因此可得到上面的结论.
(3)两圆的公共弦方程为两圆方程相减可得.
题型八:公切线问题
例59.(2022·广东·中山一中高三阶段练习)已知圆.若圆与圆有三条公切线,则的值为___________.
【答案】
【解析】由,得,
所以圆的圆心为,半径为,
因为圆,所以圆的圆心为,半径为,
因为圆与圆有三条公切线,所以圆与圆相外切,
即,解得,
所以的值为.
故答案为:.
例60.(2022·广东广州·高二期末)写出与圆和圆都相切的一条切线方程___________.
【答案】或或
【解析】圆的圆心为,半径为1;圆的圆心为,半径为4,
圆心距为,所以两圆外切,如图,有三条切线,
易得切线的方程为,
因为,且,所以,设,即,
则到的距离,解得(舍去)或,所以,
可知和关于对称,联立,解得在上,
在上任取一点,设其关于的对称点为,
则,解得,
则,所以直线,即,
综上,切线方程为或或.
故答案为:或或.
例61.(多选题)(2022·全国·高二课时练习)已知圆,圆,则下列是M,N两圆公切线的直线方程为( )
A.y=0 B.3x-4y=0 C. D.
【答案】ACD
【解析】圆M的圆心为M(2,1),半径.圆N的圆心为N(-2,-1),半径.圆心距,两圆相离,故有四条公切线.又两圆关于原点O对称,则有两条切线过原点O,设切线方程为y=kx,则圆心到直线的距离,解得k=0或,对应方程分别为y=0,4x-3y=0.另两条切线与直线MN平行,而,设切线方程为,则,解得,切线方程为,.
故选:ACD.
例62.(2022·全国·高二专题练习)若直线与圆,圆都相切,切点分别为、,则( )
A. B. C. D.
【答案】C
【解析】如下图所示,设直线交轴于点,
由于直线与圆,圆都相切,切点分别为、,
则,,,
,为的中点,为的中点,,
由勾股定理可得.
故选:C.
例63.(2022·全国·高二单元测试)已知点M,N分别在圆与圆上,则的最大值为( )
A. B.17 C. D.15
【答案】C
【解析】圆的圆心,半径,圆的圆心,半径,
则.
故选:C
例64.(多选题)(2022·全国·高二课时练习)若直线与圆相切,则直线与圆的位置关系可能是( )
A.相交 B.相切 C.相离 D.不确定
【答案】AC
【解析】由圆C的方程知其圆心C(2,1),半径为.
因为直线l与圆C相切,所以,解得.
由圆D的方程知其圆心D(2,0),半径,圆心D到直线l的距离.
当时,,即,此时直线l与圆D相离;
当时,,即,此时直线l与圆D相交.
综上所述,直线l与圆D相交或相离.
故选:AC.
例65.(2022·全国·高三专题练习)在平面直角坐标系中,圆:与圆:,则两圆的公切线的条数是( )
A.4条 B.3条 C.2条 D.1条
【答案】A
【解析】圆:的圆心,半径,
圆:的圆心,半径,
,显然,即圆与圆外离,
所以两圆的公切线的条数是4.
故选:A
例66.(2022·全国·高三专题练习)已知圆,圆,则同时与圆和圆相切的直线有( )
A.4条 B.2条 C.1条 D.0条
【答案】B
【解析】由,得圆,半径为,
由,得,半径为
所以,
,,
所以,所以圆与圆相交,
所以圆与圆有两条公共的切线.
故选:B.
例67.(2022·全国·高二课时练习)求圆与圆的公切线所在直线的方程.
【解析】由题意得,圆心为,半径,,圆心为,半径,
可知两圆的公切线所在直线的斜率存在,
设公切线所在直线的方程为,即
由,得,得或,
当时,,解得或,
当时,,解得或,
综上,两圆的公切线所在直线的方程为,,,.
例68.(2022·全国·高二专题练习)求圆与圆的内公切线所在直线方程及内公切线的长.
【解析】,,,.
设内公切线与连心线交于点,则在轴上且.
设,可得,.
设内公切线所在直线方程为,即.
由,得.
所以内公切线所在直线方程为或.
内公切线的长为.
【方法技巧与总结】
利用几何法进行转化.
题型九:圆中范围与最值问题
例69.(2022·江苏·高二专题练习)已知 ,且动点满足,则取得最小值时,点的坐标是___________.
【答案】
【解析】设,则,整理可得:;
,
当三点共线且在线段上时,取得最小值,
又直线方程为:,即,
由得:或,
又在线段上,.
故答案为:.
例70.(2022·全国·模拟预测)已知直线与圆交于不同的两点,,点,则的最大值为______.
【答案】
【解析】解 由,得.
设,,则,,
因为,所以
.
令,则,,
所以
,
当且仅当时等号成立.
所以的最大值为.
故答案为:.
例71.(2022·重庆一中高一期末)直线分别与x轴 y轴相交于A B两点,点P在圆上运动,则面积的最小值为___________.
【答案】2
【解析】直线分别与轴,轴交于,两点,
,,则,
点在圆上,
圆心为,则圆心到直线距离,
故点到直线的距离的范围为,
则.
的最小值为.
故答案为:.
例72.(2022·全国·高二课时练习)若点M为圆上任意一点,直线过定点P,则的最大值为______.
【答案】
【解析】整理直线方程得,
由,得,所以.
由圆的方程知圆心,半径,
所以.
故答案为:
例73.(2022·上海市控江中学高二期末)已知点在圆上运动,则的最大值为( )
A. B. C. D.
【答案】C
【解析】看作圆上的点到点的直线的斜率的相反数.
当经过点的直线与上半圆相切时,切线斜率最小,
设切线方程为,所以圆心到切线的距离等于半径,故,解得 故当时,切线斜率最小,此时最大,最大值为,
故选:C
例74.(2022·河南·修武一中高二开学考试(理))已知直线与圆交于两点,过分别作的垂线与轴交于两点,则当最小时,( )
A.4 B. C.8 D.
【答案】D
【解析】直线过定点,最小时,,
圆心到直线的距离,,
因为,所以此时,所以直线的倾斜角为,
过点作交于点,则,
在中,所以.
故选:D
例75.(2022·广东·佛山一中高二期中)已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形面积为( )
A. B. C. D.
【答案】C
【解析】圆的标准方程为,圆心为,半径为,
,故点在圆内,如下图所示:
则,
过点的弦过圆心时,弦长取最大值,即,
当过的弦与垂直时,弦长取最小值,即,此时,
此时,四边形的面积为.
故选:C.
例76.(2022·全国·高三专题练习)当圆的圆心到直线的距离最大时,( )
A. B. C. D.
【答案】C
【解析】因为圆的圆心为,半径,
又因为直线过定点A(-1,1),
故当与直线垂直时,圆心到直线的距离最大,
此时有,即,解得.
故选:C.
例77.(2022·全国·高二专题练习)已知圆上的点到直线的距离等于,那么的值不可以是( )
A. B. C. D.
【答案】D
【解析】直线过定点,因为,故点在圆外,
圆心,半径为,且,
所以,圆心到直线的距离的最大值为,
所以,圆上的到直线的距离的最大值为,
当直线有公共点时,圆上的到直线的距离的最小值为,
故圆上的点到直线的距离的取值范围是,
且、、,.
故选:D.
例78.(多选题)(2022·江苏·高二专题练习)圆C方程:,P为圆上的动点,则下列说法错误的是( )
A.的最大值为
B.P点到A点距离的最小值为
C.的最大值为
D.圆C的内接正三角形的面积为
【答案】BD
【解析】因为圆C方程:,
所以,圆心,半径为1,
设,当与相切时,有最值,
,,
所以的最大值为,选项A正确;
P点到A点距离的最小值为,选项B错误;
因为表示的几何意义为圆上的点与定点连线的斜率,
设,即,所以直线与圆C相切时,k有最值,
当直线与圆相切时,有,所以,
所以的最大值为,所以C选项正确;
因为圆的半径为1,所以圆C的内接正三角形的边长为,所以圆C的内接正三角形的面积为,选项D错误;
故选:BD.
例79.(2022·全国·高二课时练习)已知圆.
(1)直线过点,且与圆C相切,求直线的方程;
(2)设直线与圆C相交于M,N两点,点P为圆C上的一动点,求的面积S的最大值.
【解析】(1)由题意得C(2,0),圆C的半径为3.
当直线的斜率存在时,设直线的方程为y-l=k(x+1),即kx-y+k+1=0,
由直线与圆C相切,得,解得,所以直线的方程为4x-3y+7=0.
当直线的斜率不存在时,直线的方程为,显然与圆C相切.
综上,直线的方程为x=-1或4x-3y+7=0.
(2)由题意得圆心C到直线的距离,
设圆C的半径为r,所以r=3,所以,
点P到直线距离的最大值为,
则的面积的最大值.
【方法技巧与总结】
涉及与圆有关的最值,可借助图形性质,利用数形结合求解.一般地:
(1)形如的最值问题,可转化为动直线斜率的最值问题.
(2)形如的最值问题,可转化为动直线截距的最值问题.
(3)形如的最值问题,可转化为曲线上的点到点(a,b)的距离平方的最值问题
题型十:圆系问题
例80.(2022·全国·高二专题练习)求经过圆与直线的交点且在轴上的弦长为的圆的方程.
【解析】设所求的圆的方程为,且与轴的交点坐标为,
令得,化简得
,
由两边平方得
,化简得
解得或
所求圆的方程为,
或
所求圆的方程为或
例81.(2022·江苏·高二专题练习)已知圆:与:相交于A、B两点.
(1)求公共弦AB所在的直线方程;
(2)求圆心在直线y=-x上,且经过A、B两点的圆的方程;
(3)求经过A、B两点且面积最小的圆的方程.
【解析】(1)将两圆方程相减得x-2y+4=0,此即为所求直线方程.
(2)设经过A、B两点的圆的方程为(为常数),
则圆心坐标为;又圆心在直线y=-x上,故,
解得,故所求方程为.
(3)由题意可知以线段AB为直径的圆面积最小.两圆心所在直线方程为2x+y+3=0,
与直线AB方程联立得所求圆心坐标为,由弦长公式可知所求圆的半径为.
故面积最小的圆的方程为.
例82.过圆与的交点,且圆心在直线上的圆的方程是_______.
【答案】
【解析】
设圆的方程为,
则,
即,所以圆心坐标为,
把圆心坐标代入,可得,
所以所求圆的方程为.
故答案为:.
例83.已知圆与圆相交于A、B两点.
(1)求公共弦AB所在直线方程;
(2)求过两圆交点A、B,且过原点的圆的方程.
【解析】(1),①
,②
①-②得
即公共弦AB所在直线方程为.
(2)设圆的方程为
即
因为圆过原点,所以,
所以圆的方程为
【方法技巧与总结】
圆系方程:若圆与圆相交于A,B两点,则过A,B两点的圆系方程为:
简记为:,不含
当时,该圆系退化为公共弦所在直线(根轴)
注意:与圆C共根轴l的圆系
【同步练习】
一、单选题
1.设圆,圆,则圆,的公切线有( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】由题意,得圆,圆心,圆,圆心,∴,∴与相交,有2条公切线.
故选:B.
2.求与直线平行且将圆的周长平分的直线方程为( )
A. B.
C. D.
【答案】C
【解析】圆的圆心坐标,
所求直线将圆平分,
则直线过圆的圆心,
又因为与直线平行,则所求直线的斜率为,
利用点斜式得到直线方程为,整理成一般式为
故选:C
3.直线绕原点按逆时针方向旋转后所得的直线l与圆的位置关系是( )
A.直线l过圆心 B.直线l与圆相交,但不过圆心
C.直线l与圆相切 D.直线l与圆无公共点
【答案】C
【解析】直线过原点,斜率为,倾斜角为,依题意,直线l的倾斜角为,斜率为,而l过原点,
因此,直线l的方程为:,又圆的圆心为,半径为,
于是得点到直线l的距离为,所以直线l与圆相切.
故选:C
4.设是圆上的动点,是圆的切线,且,则点到点距离的最小值为( )
A.4 B.5 C.6 D.15
【答案】B
【解析】由圆,可知圆心,半径为3,又,
所以,即点的轨迹方程为,
故点到点距离的最小值为.
故选:B.
5.已知直线l:与圆O:相交于不同的两点A,B,若∠AOB为锐角,则m的取值范围为( )
A. B.
C. D.
【答案】A
【解析】因为直线l:经过定点,圆O:的半径为,
当∠AOB为直角时,此时圆心O到直线l的距离,解得,
则当∠AOB为锐角时,.
又直线与圆相交于A,B两点,则,即,
所以或,
故选:A.
6.若点C到的距离之比为,则点C到直线的距离的最小值为( )
A. B. C. D.
【答案】A
【解析】设,则,即,化简得,
所以点的轨迹为以为圆心,的圆,
则圆心到直线的距离,
所以点C到直线的距离的最小值为;
故选:A.
7.古希腊数学家阿波罗尼斯(约前262—前190年)的著作《圆锥曲线论》是古代光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数且的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.已知,,圆上有且仅有一个点P满足,则r的取值为( )
A.1 B.5 C.1或5 D.不存在
【答案】C
【解析】设点P
∵即
整理得:
∴点P的轨迹为以为圆心,半径的圆,
∵圆的为圆心,半径的圆
由题意可得:或
∴或
故选:C.
8.从空中某个角度俯视北京冬奥会主体育场“鸟巢”顶棚所得的局部示意图如图,在平面直角坐标系中,下列直线系方程(其中为参数,)能形成这种效果的是( )
A. B.
C. D.
【答案】C
【解析】由图可知,原点到直线的距离为定值,四个选项中仅有到原点的距离为定值.
故选:C
二、多选题
9.已知圆与圆有四条公切线,则实数a的取值可能是( )
A.-4 B.-2 C. D.3
【答案】AD
【解析】圆心,半径,圆心,半径.因为两圆有四条公切线,所以两圆外离.又两圆圆心距,所以,解得或.
故选:AD.
10.已知圆C:,则下列四个命题表述正确的是( )
A.圆C上有且仅有3个点到直线1:的距离都等于1
B.过点作圆C的两条切线,切点分别为M,N,直线MN的方程为
C.一条直线与圆C交于不同的两点P,Q,且有,则∠PCQ的最大值为
D.若圆C与E:相外切,则
【答案】BC
【解析】圆C的圆心,半径,
圆心到直线l:的距离,故圆C上有4个点到直线l的距离为1,故A不正确;
过点作圆C的两条切线,切点分别为M,N,则A、C、M、N四点共圆,且为AC为直径,方程为,MN是其圆C的公共弦,直线MN为,故B正确;
设PQ的中点为D,则.因为,
即,可得,
则,故的最大值为,故C正确;
圆E:的圆心,半径
根据题意可得,即得,故D错误.
故选:BC.
11.已知M为圆C:上的动点,P为直线l:上的动点,则下列结论正确的是( )
A.直线l与圆C相切 B.直线l与圆C相离
C.|PM|的最大值为 D.|PM|的最小值为
【答案】BD
【解析】圆C:得圆心,半径
∵圆心到直线l:得距离
∴直线l与圆C相离
A不正确,B正确;
C不正确,D正确;
故选:BD.
12.若实数x,y满足,则下列说法正确的是( )
A.x的最小值是4
B.x的最大值是20
C.若关于y的方程有一解,则x的取值范围为
D.若关于y的方程有两解,则x的取值范围为
【答案】BD
【解析】当时,解得,符合题意;当时,令,则,又,则,即,则原方程可化为.设,,,则的图象是斜率为的直线的一部分,的图象是以原点为圆心,半径为的四分之一圆,则问题等价于的图象和的图象有公共点,观察图形可知,
当直线与圆相切时,由,解得;当直线过点时,,解得;当直线过点时,,解得.因此,要使直线与圆有公共点,则有,综上,,故x的最大值为20,最小值为0.显然当或或时,y有一解;当时,y有两解.
故选:BD.
三、填空题
13.大约在2000多年前,我国的墨子给出了圆的概念“一中同长也”,意思是说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下定义要早100多年.已知直角坐标平面内有一点和一动点满足,若过点的直线将动点的轨迹分成两段弧,当劣弧所对的圆心角最小时,直线的斜率__________.
【答案】
【解析】依题意可知,动点的轨迹是以为圆心,为半径的圆,
即.
因为,故点在内.
当劣弧所对的圆心角最小时,.
因为直线的斜率,
所以所求直线的斜率.
故答案为:.
14.规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置,球是指该球的球心点.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为1的圆,且母球与目标球有公共点时,目标球就开始运动,在桌面上建立平面直角坐标系,如图,设母球的位置为(0,0),目标球的位置为,要使目标球向处运动,则母球的球心运动的直线方程为______.
【答案】
【解析】点,所在直线的方程为,如图所示
可知,两球碰撞时,球的球心在直线上,且在第一象限,设,两球碰撞时,球的球心坐标为,此时,则,解得,即,B两球碰撞时,球的球心坐标
所以母球的球心运动的直线方程为,即.
故答案为:
15.直线与半圆有两个交点,则的值是____.
【答案】
【解析】由半圆,即,
如图所示,当直线在第三象限与半圆相切时,圆心到直线的距离,
即,解得:或(舍去),
当直线过点时,直线与圆有两个交点和,
把代入中,可得 ,解得,
则直线与圆有两个交点时,的范围是.
故答案为:
16.设直线系,对于下列四个命题:
①M中所有直线均经过一个定点;
②存在定点P不在M中的任一条直线上;
③对于任意整数,存在正n边形,使其所有边均在M中的直线上;
④M中的直线所能围成的正三角形面积都相等.
其中真命题的序号是_________(写出所有真命题的序号)
【答案】②③
【解析】由直线系,
可令,消去可得,
故直线系表示圆的切线的集合,故①不正确;
因为对任意,存在定点不在直线系中的任意一条上,故②正确;
由于圆的外切正边形,所有的边都在直线系中,故③正确;
中的直线所能围成的正三角形的边长不一定相等,故它们的面积不一定相等,如图中等边三角形和面积不相等,故④不正确.
综上,正确的命题是②③.
故答案为:②③.
四、解答题
17.从①与直线4x-3y+5=0垂直,②过点(5,-5),③与直线3x+4y+2=0平行这三个条件中任选一个,补充在下面的问题中,并加以解答.
问题:已知直线l过点,且______.
(1)求直线l的一般式方程;
(2)若直线l与圆相交于点P,Q,求弦PQ的长.
注:如果选择多个条件分别解答,按第一个解答计分.
【解析】(1)方案一:选条件①.
(1)因为直线4x-3y+5=0的斜率为,且与直线l垂直,所以直线l的斜率为,
依题意,直线l的方程为,即3x+4y+5=0.
方案二:选条件②.
(1)因为直线l过点(5,-5)及(1,-2),
所以直线l的方程为,即.
方案三:选条件③.
(1)因为直线3x+4y+2=0的斜率为,直线l与直线3x+4y+2=0平行,
所以直线l的斜率为.
依题意,直线l的方程为,即3x+4y+5=0.
(2)方案一:选条件①.
(2)圆的圆心(0,0)到直线3x+4y+5=0的距离为.
又圆的半径为,所以.
方案二:选条件②.
(2)解析同方案一中(2).
方案三:选条件③.
(2)解析同方案一中(2).
18.在①,②最小,③过A,B两点分别作圆C的切线,切线交于点P(2,0)这三个条件中任选一个,补充在下面问题中,并求解.
在平面直角坐标系中,已知圆,直线l过定点M(1,1).设直线l与圆C交于A,B两点,当______时,求直线l的方程.
【解析】将圆的方程化为,则C(0,2),半径r=2.
方案一:选条件①.
因为,所以,所以.
当直线l的斜率不存在时,方程为x=1,此时,不符合题意.
当直线l的斜率存在时,设方程为,即,
由题意可知,即,解得k=1,所以直线.
方案二:选条件②.
当直线所过定点M(1,1)为弦AB的中点时,最小,此时,,所以直线l的斜率为1,所以直线.
方案三:选条件③.
因为过A,B两点分别作圆C的切线,切线交于P(2,0),所以,,所以直线l的斜率为1,又直线过定点M(1,1),所以直线.
19.已知圆,平面上一动点P满足:且,.
(1)求动点P的轨迹方程;
(2)过点N的直线l(斜率为正)交圆G于A C两点,交P的轨迹于B D两点(A B在第一象限),若,求直线l的方程.
【解析】(1)设,则,
整理得:.
(2)由题知l斜率为正,设直线,
则原点到直线l的距离为:,
故,
又圆,所以圆心,半径为2,
所以G到直线l的距离为:,
故,
又,所以,
所以,
整理得:,
解得:,(舍负),
所以直线l的方程为:.
20.已知直线过定点,且与圆交于、两点.
(1)求直线的斜率的取值范围.
(2)若为坐标原点,直线、的斜率分别为、,试问是否为定值?若是,求出该定值;若不是,请说明理由.
【解析】(1)圆的标准方程为,圆心为,半径为.
若直线的斜率不存在,此时直线与圆相切,不合乎题意.
所以,直线的斜率存在,设直线的方程为,
由题意可得,解得.
因此,直线的斜率的取值范围是.
(2)设,,设直线的方程为.
联立,得,其中,
所以,,
则,
所以为定值.
21.在平面直角坐标系中,光线过点,经轴反射后与圆:有交点
(1)当反射后光线经过圆心,求光线的方程;
(2)当反射后光线与圆相切,求光线的方程.
【解析】(1)点关于轴对称的点为,由光线的折射性质,反射光线经过圆心,所以,
易知,所以,
所以光线的方程为.
(2)设经过的直线方程为由于折射光线与圆相切,
所以圆心到直线的距离等于半径,即,
化简得:,
解得或,
所光线的方程为或.
22.如图,在平面直角坐标系上,已知圆的直径,定直线到圆心的距离为,且直线垂直于直线,点是圆上异于、的任意一点,直线、分别交与、两点.
(1)求过点且与圆相切的直线方程;
(2)若,求以为直径的圆方程;
(3)当点变化时,以为直径的圆是否过圆内的一定点,若过定点,请求出定点;若不过定点,请说明理由.
【解析】(1)易知圆的方程为,圆心为原点,半径为,
若所求直线的斜率不存在,则所求直线的方程为,此时直线与圆相切,合乎题意,
若所求直线的斜率存在,设所求直线的方程为,即,
由已知可得,解得,此时所求直线的方程为.
综上所述,过点且与圆相切的直线方程为或.
(2)易知直线的方程为,、,
若点在轴上方,则直线的方程为,
在直线的方程中,令,可得,即点,
直线的方程为,
在直线的方程中,令,可得,即点,
线段的中点为,且,此时,所求圆的方程为;
若点在轴下方,同理可求得所求圆的方程为.
综上所述,以为直径的圆方程为.
(3)不妨设直线的方程为,其中,
在直线的方程中,令,可得,即点,
因为,则直线的方程为,
在直线的方程中,令,可得,即点,
线段的中点为,,
所以,以线段为直径的圆的方程为,
即,由,解得,
因此,当点变化时,以为直径的圆是否过圆内的定点
【知识点梳理】
知识点一:直线与圆的位置关系
1.直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2.直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
知识点诠释:
(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.
(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.
(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.
知识点二:圆的切线方程的求法
1.点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率
的乘积等于,即.
法二:圆心到直线的距离等于半径.
2.点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
知识点诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是
.
知识点三:求直线被圆截得的弦长的方法
1.应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
2.利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
知识点四:圆与圆的位置关系
1.圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
2.圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
知识点诠释:
判定圆与圆的位置关系主要是利用几何法,通过比较两圆的圆心距和两圆的半径的关系来确定,这种方法运算量小.也可利用代数法,但是利用代数法解决时,一是运算量大,二是方程组仅有一解或无解时,两圆的位置关系不明确,还要比较两圆的圆心距和两圆半径的关系来确定.因此,在处理圆与圆的位置关系时,一般不用代数法.
3.两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
4.两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
【题型归纳目录】
题型一:不含参数(含参数)的直线与圆的位置关系
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
题型三:切线与切线长问题
题型四:弦长问题
题型五:判断圆与圆的位置关系
题型六:由圆的位置关系确定参数
题型七:公共弦与切点弦问题
题型八:公切线问题
题型九:圆中范围与最值问题
题型十:圆系问题
【典型例题】
题型一:不含参数(含参数)的直线与圆的位置关系
例1.(2022·全国·高二课时练习)直线和圆的位置关系为( )
A.相交 B.相切或相交 C.相离 D.相切
例2.(2022·西藏·林芝市第二高级中学高一期末)圆x2+y2-2x+4y=0与直线2x+y+1=0的位置关系为( )
A.相离 B.相切 C.相交 D.以上都有可能
例3.(2022·全国·高三专题练习)直线与圆的位置关系为( )
A.相切 B.相交
C.相离 D.由的取值确定
例4.(2022·全国·高二专题练习)圆与直线的位置关系为( )
A.相切 B.相离 C.相交 D.无法确定
【方法技巧与总结】
直线与圆的位置关系判断方法
法一抓住直线与圆的位置关系的代数特征,从而转化为对方程的解的研究,这是研究直线与曲线的位置关系的基本方法;法二抓住直线与圆的位置关系的几何特征,从而转化为研究圆心到直线的距离,抓住几何特征对于研究圆的问题特别有效;法三通过判定直线过圆内一定点,从而使问题获证.由上述三种解法可知,解题的切入点不同,解法就有优劣之分.因此,在解题时,审题要慢,要仔细地分析题意,透彻地理解题意,挖掘其中的隐含条件,从而找到解决问题的捷径.
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
例5.(2022·福建省福州第二中学高二期末)已知直线平分圆:,则的最大值为( )
A. B. C. D.
例6.(2022·全国·高二课时练习)若直线与曲线有两个交点,则实数的取值范围是( )
A. B.
C. D.
例7.(2022·全国·高三专题练习)若直线y=x+b与曲线x恰有一个公共点,则b的取值范围是( )
A.﹣1<b≤1 B.﹣1≤b≤1
C.b≤﹣1 D.﹣1<b≤1或b
例8.(2022·全国·高三专题练习)若方程有两个不等的实根,则实数b的取值范围为( )
A. B. C. D.
例9.(2022·全国·高三专题练习)已知直线与圆相交于,两点,则的值为( )
A. B.16 C. D.8
例10.(2022·全国·高三专题练习)已知圆上仅有一点到直线的距离为1,则实数a的值为( ).
A.11 B. C.1 D.4
例11.(2022·全国·高三专题练习)如果圆上总存在两个点到原点的距离为,则实数的取值范围是( )
A. B.
C. D.
例12.(2022·全国·高三专题练习)若直线 与圆 相交于 两点, 且 (其中 为原点), 则 的值为( )
A. 或 B. C. 或 D.
例13.(2022·全国·高三专题练习)已知直线过点且斜率为1,若圆上恰有3个点到的距离为1,则的值为( )
A. B. C. D.
例14.(2022·全国·高二课时练习)若圆上存在四个点到直线的距离为,则实数m的取值范围是( )
A. B.
C. D.或
例15.(2022·江西·南昌大学附属中学高二期末(理))已知圆上有三个点到直线的距离等于1,则的值为( )
A. B. C. D.1
例16.(2022·四川省绵阳南山中学高二阶段练习(文))已知直线:和圆:,且圆上至少存在两点到直线的距离为1,则的取值范围是( )
A. B.
C. D.
例17.(2022·全国·高二课时练习)若圆与轴、轴均有公共点,则实数的取值范围是______.
【方法技巧与总结】
直接联立求解.
题型三:切线与切线长问题
例18.(2022·全国·高三专题练习)已知圆:,为过的圆的切线,为上任一点,过作圆:的切线,则切线长的最小值是__________.
例19.(2022·天津市武清区杨村第一中学模拟预测)由直线上的点向圆引切线(为切点),则线段的最小长度为________.
例20.(2022·云南玉溪·高二期末)已知直线经过点,且与圆相切,则的方程为( )
A. B. C. D.
例21.(2022·辽宁·大连市一0三中学模拟预测)过点作圆的切线,则切线方程为( )
A. B. C. D.或
例22.(2022·全国·高三专题练习)已知圆.求满足下列条件的切线方程.
(1)过点;
(2)过点.
例23.(2022·江苏连云港·模拟预测)直线与圆相切,则的值为( )
A. B.1 C. D.
例24.(多选题)(2022·全国·高二课时练习)过点作与圆相切的直线l,则直线l的方程为( )
A. B.
C. D.
例25.(多选题)(2022·全国·高二单元测试)设有一组圆Ck:,下列说法正确的是( )
A.这组圆的半径均为1
B.直线2x-y+2=0平分所有的圆Ck
C.存在无穷多条直线l被所有的圆Ck截得的弦长相等
D.存在一个圆Ck与x轴与y轴均相切
【方法技巧与总结】
求圆的切线方程一般有三种方法:
(1)直接法:应用常见结论,直接写出切线方程;
(2)待定系数法;
(3)定义法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.
题型四:弦长问题
例26.(2022·安徽省太和中学高三阶段练习)在平面直角坐标系中,圆被直线截得的弦长2,则实数的值为___________.
例27.(2022·河南·高三阶段练习(文))直线与圆C:相交于M,N两点,则______.
例28.(2022·全国·高二课时练习)设圆的圆心为C,直线l过,且与圆C交于A,B两点,若,则直线l的方程为___________.
例29.(2022·全国·高三专题练习)在平面直角坐标系中,已知直线与圆交于A,B两点,若钝角的面积为,则实数a的值是______.
例30.(2022·全国·模拟预测)在平面直角坐标系xOy中,过点的直线l与圆相交于M,N两点,若,则直线l的斜率为__________.
例31.(2022·全国·高二专题练习)已知圆,直线l过点且与圆O交于A,B两点,当面积最大时,直线l的方程为_________.
例32.(多选题)(2022·湖南·华容县教育科学研究室高一期末)已知动直线与圆,则下列说法正确的是( )
A.直线过定点
B.圆的圆心坐标为
C.直线与圆的相交弦的最小值为
D.直线与圆的相交弦的最大值为4
例33.(多选题)(2022·全国·高二课时练习)若直线被圆所截得的弦长为,则实数a的值为( )
A.0 B.4 C. D.
例34.(多选题)(2022·河南·范县第一中学高二阶段练习)在平面直角坐标系中,O为坐标原点,已知圆O半径为3,直线l1、l2互相垂直,垂足为M(1,2),且l1与圆O相交于A、C两点,l2与圆O交于B、D两点,则四边形ABCD面积的值可以为( )
A.11 B.12 C.13 D.14
例35.(2022·全国·高二课时练习)若直线被圆截得的弦长不大于,求实数的取值范围.
【方法技巧与总结】
弦长问题
①利用垂径定理:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
②利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
③利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:.
题型五:判断圆与圆的位置关系
例36.(2022·全国·高二课时练习)已知圆和,则两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
例37.(2022·全国·高三专题练习)已知两圆分别为圆和圆,这两圆的位置关系是( )
A.相离 B.相交 C.内切 D.外切
例38.(2022·陕西·铜川阳光中学高一期末)已知圆(,为常数)与.若圆心与圆心关于直线对称,则圆与的位置关系是( )
A.内含 B.相交 C.内切 D.相离
【方法技巧与总结】
已知两圆半径分别为,两圆的圆心距为,则:
(1)两圆外离;
(2)两圆外切;
(3)两圆相交;
(4)两圆内切;
(5)两圆内含;
题型六:由圆的位置关系确定参数
例39.(2022·云南省下关第一中学高三开学考试)若圆上总存在两个点到点的距离为2,则实数a的取值范围是( )
A. B.
C. D.
例40.(2022·湖北·荆门市龙泉中学二模)若点到直线的距离分别为1和4,则这样的直线共有( )条
A.4 B.3 C.2 D.1
例41.(2022·浙江·乐清市知临中学高二期中)已知,两点到直线的距离分别是2和3,则满足条件的直线共有( )条.
A.1 B.2 C.3 D.4
例42.(2022·全国·高三专题练习)已知圆和两点,,.若圆上存在点,使得,则的最小值为( )
A.7 B.6 C.5 D.4
例43.(2022·山东聊城·二模)已知点在圆:上,点,,满足的点的个数为( )
A.3 B.2 C.1 D.0
例44.(2022·全国·高三专题练习)若圆上存在点P,且点P关于直线y=x的对称点Q在圆上,则r的取值范围是( )
A. B. C. D.
【方法技巧与总结】
利用几何法判定两圆的位置关系比用代数法(即解两圆方程联立方程组的方法)要简捷些,但需要注意的是,我们这里所说的几何法仍然是在解析几何前提下的几何法,即利用圆的方程及两点间距离公式求出两圆圆心距d和两圆的半径R和r,再根据d与、d与的大小关系来判定即可.
题型七:公共弦与切点弦问题
例45.(2022·广东·高三阶段练习)已知:,直线:,为直线上的动点,过点作的切线,,切点为,,当四边形的面积取最小值时,直线AB的方程为 ____.
例46.(2022·江苏·高二专题练习)已知圆的方程为,点是直线上的一个动点,过点作圆的两条切线、,、为切点,则四边形的面积的最小值为______
例47.(2022·云南·昆明一中高三开学考试)已知圆和圆交于两点,则直线的方程是___________.
例48.(2022·全国·高三专题练习)圆与圆的公共弦长为______.
例49.(2022·全国·高三专题练习)已知圆:,点是直线上的动点,过作圆的两条切线,切点分别为,,则的最小值为( )
A. B. C. D.
例50.(2022·全国·高三专题练习)已知圆,点M为直线上一个动点,过点M作圆C的两条切线,切点分别为A,B,则四边形周长的最小值为( )
A.8 B. C. D.
例51.(2022·全国·高二课时练习)已知点P为直线上的动点,过点P作圆的两条切线,切点分别为A B,则直线必过定点( )
A. B. C. D.
例52.(2022·安徽·屯溪一中高二期中)已知直线是圆的对称轴.过点作圆的两条切线,切点分别为、,则直线的方程为( )
A. B. C. D.
例53.(2022·四川省绵阳第一中学高二期中)过点作圆C:的两条切线,切点分别为A,B,则直线AB的方程为( )
A. B. C. D.
例54.(2022·江苏常州·一模)过圆:外一点作圆的切线,切点分别为、,则( )
A.2 B. C. D.3
例55.(2022·江苏·高二专题练习)已知圆M:,直线l:,P为直线l上的动点,过P点作圆M的切线PA、PB,切点为A、B,当最小时,直线AB的方程为( )
A. B.
C. D.
例56.(多选题)(2022·全国·高二课时练习)圆和圆的交点为A,B,则有( )
A.公共弦AB所在直线的方程为
B.公共弦AB所在直线的方程为
C.公共弦AB的长为
D.P为圆上一动点,则P到直线AB距离的最大值为
例57.(2022·广东·汕头市潮阳区棉城中学高二期中)过直线上任意点作圆的两条切线,切点分别为,当切线长最小时,切线长为_________;同时 的面积为_______.
例58.(2022·浙江绍兴·模拟预测)已知圆C的方程为,则圆心C的坐标为___________,圆C与圆D:的公共弦所在直线方程为___________.
【方法技巧与总结】
(1)圆的切线方程的求法
①点在圆上,
法一:利用切线的斜率与圆心和该点连线的斜率的乘积等于,即.
法二:圆心到直线的距离等于半径.
②点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
注意:因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
(2)常见圆的切线方程
过圆上一点的切线方程是;
过圆上一点的切线方程是.
过圆外一点作圆的两条切线,则两切点所在直线方程为
过曲线上,做曲线的切线,只需把替换为,替换为,替换为,替换为即可,因此可得到上面的结论.
(3)两圆的公共弦方程为两圆方程相减可得.
题型八:公切线问题
例59.(2022·广东·中山一中高三阶段练习)已知圆.若圆与圆有三条公切线,则的值为___________.
例60.(2022·广东广州·高二期末)写出与圆和圆都相切的一条切线方程___________.
例61.(多选题)(2022·全国·高二课时练习)已知圆,圆,则下列是M,N两圆公切线的直线方程为( )
A.y=0 B.3x-4y=0 C. D.
例62.(2022·全国·高二专题练习)若直线与圆,圆都相切,切点分别为、,则( )
A. B. C. D.
例63.(2022·全国·高二单元测试)已知点M,N分别在圆与圆上,则的最大值为( )
A. B.17 C. D.15
例64.(多选题)(2022·全国·高二课时练习)若直线与圆相切,则直线与圆的位置关系可能是( )
A.相交 B.相切 C.相离 D.不确定
例65.(2022·全国·高三专题练习)在平面直角坐标系中,圆:与圆:,则两圆的公切线的条数是( )
A.4条 B.3条 C.2条 D.1条
例66.(2022·全国·高三专题练习)已知圆,圆,则同时与圆和圆相切的直线有( )
A.4条 B.2条 C.1条 D.0条
例67.(2022·全国·高二课时练习)求圆与圆的公切线所在直线的方程.
例68.(2022·全国·高二专题练习)求圆与圆的内公切线所在直线方程及内公切线的长.
【方法技巧与总结】
利用几何法进行转化.
题型九:圆中范围与最值问题
例69.(2022·江苏·高二专题练习)已知 ,且动点满足,则取得最小值时,点的坐标是___________.
例70.(2022·全国·模拟预测)已知直线与圆交于不同的两点,,点,则的最大值为______.
例71.(2022·重庆一中高一期末)直线分别与x轴 y轴相交于A B两点,点P在圆上运动,则面积的最小值为___________.
例72.(2022·全国·高二课时练习)若点M为圆上任意一点,直线过定点P,则的最大值为______.
例73.(2022·上海市控江中学高二期末)已知点在圆上运动,则的最大值为( )
A. B. C. D.
例74.(2022·河南·修武一中高二开学考试(理))已知直线与圆交于两点,过分别作的垂线与轴交于两点,则当最小时,( )
A.4 B. C.8 D.
例75.(2022·广东·佛山一中高二期中)已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形面积为( )
A. B. C. D.
例76.(2022·全国·高三专题练习)当圆的圆心到直线的距离最大时,( )
A. B. C. D.
例77.(2022·全国·高二专题练习)已知圆上的点到直线的距离等于,那么的值不可以是( )
A. B. C. D.
例78.(多选题)(2022·江苏·高二专题练习)圆C方程:,P为圆上的动点,则下列说法错误的是( )
A.的最大值为
B.P点到A点距离的最小值为
C.的最大值为
D.圆C的内接正三角形的面积为
例79.(2022·全国·高二课时练习)已知圆.
(1)直线过点,且与圆C相切,求直线的方程;
(2)设直线与圆C相交于M,N两点,点P为圆C上的一动点,求的面积S的最大值.
【方法技巧与总结】
涉及与圆有关的最值,可借助图形性质,利用数形结合求解.一般地:
(1)形如的最值问题,可转化为动直线斜率的最值问题.
(2)形如的最值问题,可转化为动直线截距的最值问题.
(3)形如的最值问题,可转化为曲线上的点到点(a,b)的距离平方的最值问题
题型十:圆系问题
例80.(2022·全国·高二专题练习)求经过圆与直线的交点且在轴上的弦长为的圆的方程.
例81.(2022·江苏·高二专题练习)已知圆:与:相交于A、B两点.
(1)求公共弦AB所在的直线方程;
(2)求圆心在直线y=-x上,且经过A、B两点的圆的方程;
(3)求经过A、B两点且面积最小的圆的方程.
例82.过圆与的交点,且圆心在直线上的圆的方程是_______.
例83.已知圆与圆相交于A、B两点.
(1)求公共弦AB所在直线方程;
(2)求过两圆交点A、B,且过原点的圆的方程.
【方法技巧与总结】
圆系方程:若圆与圆相交于A,B两点,则过A,B两点的圆系方程为:
简记为:,不含
当时,该圆系退化为公共弦所在直线(根轴)
注意:与圆C共根轴l的圆系
【同步练习】
一、单选题
1.设圆,圆,则圆,的公切线有( )
A.1条 B.2条 C.3条 D.4条
2.求与直线平行且将圆的周长平分的直线方程为( )
A. B.
C. D.
3.直线绕原点按逆时针方向旋转后所得的直线l与圆的位置关系是( )
A.直线l过圆心 B.直线l与圆相交,但不过圆心
C.直线l与圆相切 D.直线l与圆无公共点
4.设是圆上的动点,是圆的切线,且,则点到点距离的最小值为( )
A.4 B.5 C.6 D.15
5.已知直线l:与圆O:相交于不同的两点A,B,若∠AOB为锐角,则m的取值范围为( )
A. B.
C. D.
6.若点C到的距离之比为,则点C到直线的距离的最小值为( )
A. B. C. D.
7.古希腊数学家阿波罗尼斯(约前262—前190年)的著作《圆锥曲线论》是古代光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数且的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.已知,,圆上有且仅有一个点P满足,则r的取值为( )
A.1 B.5 C.1或5 D.不存在
8.从空中某个角度俯视北京冬奥会主体育场“鸟巢”顶棚所得的局部示意图如图,在平面直角坐标系中,下列直线系方程(其中为参数,)能形成这种效果的是( )
A. B.
C. D.
二、多选题
9.已知圆与圆有四条公切线,则实数a的取值可能是( )
A.-4 B.-2 C. D.3
10.已知圆C:,则下列四个命题表述正确的是( )
A.圆C上有且仅有3个点到直线1:的距离都等于1
B.过点作圆C的两条切线,切点分别为M,N,直线MN的方程为
C.一条直线与圆C交于不同的两点P,Q,且有,则∠PCQ的最大值为
D.若圆C与E:相外切,则
11.已知M为圆C:上的动点,P为直线l:上的动点,则下列结论正确的是( )
A.直线l与圆C相切 B.直线l与圆C相离
C.|PM|的最大值为 D.|PM|的最小值为
12.若实数x,y满足,则下列说法正确的是( )
A.x的最小值是4
B.x的最大值是20
C.若关于y的方程有一解,则x的取值范围为
D.若关于y的方程有两解,则x的取值范围为
三、填空题
13.大约在2000多年前,我国的墨子给出了圆的概念“一中同长也”,意思是说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下定义要早100多年.已知直角坐标平面内有一点和一动点满足,若过点的直线将动点的轨迹分成两段弧,当劣弧所对的圆心角最小时,直线的斜率__________.
14.规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置,球是指该球的球心点.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为1的圆,且母球与目标球有公共点时,目标球就开始运动,在桌面上建立平面直角坐标系,如图,设母球的位置为(0,0),目标球的位置为,要使目标球向处运动,则母球的球心运动的直线方程为______.
15.直线与半圆有两个交点,则的值是____.
16.设直线系,对于下列四个命题:
①M中所有直线均经过一个定点;
②存在定点P不在M中的任一条直线上;
③对于任意整数,存在正n边形,使其所有边均在M中的直线上;
④M中的直线所能围成的正三角形面积都相等.
其中真命题的序号是_________(写出所有真命题的序号)
四、解答题
17.从①与直线4x-3y+5=0垂直,②过点(5,-5),③与直线3x+4y+2=0平行这三个条件中任选一个,补充在下面的问题中,并加以解答.
问题:已知直线l过点,且______.
(1)求直线l的一般式方程;
(2)若直线l与圆相交于点P,Q,求弦PQ的长.
注:如果选择多个条件分别解答,按第一个解答计分.
18.在①,②最小,③过A,B两点分别作圆C的切线,切线交于点P(2,0)这三个条件中任选一个,补充在下面问题中,并求解.
在平面直角坐标系中,已知圆,直线l过定点M(1,1).设直线l与圆C交于A,B两点,当______时,求直线l的方程.
19.已知圆,平面上一动点P满足:且,.
(1)求动点P的轨迹方程;
(2)过点N的直线l(斜率为正)交圆G于A C两点,交P的轨迹于B D两点(A B在第一象限),若,求直线l的方程.
20.已知直线过定点,且与圆交于、两点.
(1)求直线的斜率的取值范围.
(2)若为坐标原点,直线、的斜率分别为、,试问是否为定值?若是,求出该定值;若不是,请说明理由.
21.在平面直角坐标系中,光线过点,经轴反射后与圆:有交点
(1)当反射后光线经过圆心,求光线的方程;
(2)当反射后光线与圆相切,求光线的方程.
22.如图,在平面直角坐标系上,已知圆的直径,定直线到圆心的距离为,且直线垂直于直线,点是圆上异于、的任意一点,直线、分别交与、两点.
(1)求过点且与圆相切的直线方程;
(2)若,求以为直径的圆方程;
(3)当点变化时,以为直径的圆是否过圆内的一定点,若过定点,请求出定点;若不过定点,请说明理由
2.5 直线与圆、圆与圆的位置关系
【知识点梳理】
知识点一:直线与圆的位置关系
1.直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2.直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
知识点诠释:
(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.
(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.
(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.
知识点二:圆的切线方程的求法
1.点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率
的乘积等于,即.
法二:圆心到直线的距离等于半径.
2.点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
知识点诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是
.
知识点三:求直线被圆截得的弦长的方法
1.应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
2.利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
知识点四:圆与圆的位置关系
1.圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
2.圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
知识点诠释:
判定圆与圆的位置关系主要是利用几何法,通过比较两圆的圆心距和两圆的半径的关系来确定,这种方法运算量小.也可利用代数法,但是利用代数法解决时,一是运算量大,二是方程组仅有一解或无解时,两圆的位置关系不明确,还要比较两圆的圆心距和两圆半径的关系来确定.因此,在处理圆与圆的位置关系时,一般不用代数法.
3.两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
4.两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
【题型归纳目录】
题型一:不含参数(含参数)的直线与圆的位置关系
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
题型三:切线与切线长问题
题型四:弦长问题
题型五:判断圆与圆的位置关系
题型六:由圆的位置关系确定参数
题型七:公共弦与切点弦问题
题型八:公切线问题
题型九:圆中范围与最值问题
题型十:圆系问题
【典型例题】
题型一:不含参数(含参数)的直线与圆的位置关系
例1.(2022·全国·高二课时练习)直线和圆的位置关系为( )
A.相交 B.相切或相交 C.相离 D.相切
【答案】A
【解析】由,得,
所以圆心为,半径为.
因为圆心到直线的距离为
,
所以直线和圆相交.
故选:A
例2.(2022·西藏·林芝市第二高级中学高一期末)圆x2+y2-2x+4y=0与直线2x+y+1=0的位置关系为( )
A.相离 B.相切 C.相交 D.以上都有可能
【答案】C
【解析】圆x2+y2-2x+4y=0的圆心坐标为,半径
圆心到直线2x+y+1=0的距离
由,可得圆与直线的位置关系为相交.
故选:C
例3.(2022·全国·高三专题练习)直线与圆的位置关系为( )
A.相切 B.相交
C.相离 D.由的取值确定
【答案】A
【解析】因为圆心到直线的距离,即为圆的半径,所以可知直线与圆相切.
故选:A.
例4.(2022·全国·高二专题练习)圆与直线的位置关系为( )
A.相切 B.相离 C.相交 D.无法确定
【答案】C
【解析】直线可化为,所以恒过定点.
把代入,有:,
所以在圆内,所以圆与直线的位置关系为相交.
故选:C
【方法技巧与总结】
直线与圆的位置关系判断方法
法一抓住直线与圆的位置关系的代数特征,从而转化为对方程的解的研究,这是研究直线与曲线的位置关系的基本方法;法二抓住直线与圆的位置关系的几何特征,从而转化为研究圆心到直线的距离,抓住几何特征对于研究圆的问题特别有效;法三通过判定直线过圆内一定点,从而使问题获证.由上述三种解法可知,解题的切入点不同,解法就有优劣之分.因此,在解题时,审题要慢,要仔细地分析题意,透彻地理解题意,挖掘其中的隐含条件,从而找到解决问题的捷径.
题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标
例5.(2022·福建省福州第二中学高二期末)已知直线平分圆:,则的最大值为( )
A. B. C. D.
【答案】B
【解析】圆:,圆心,
直线平分圆:,
直线过圆心,即,
,
当且仅当,即,的最大值为.
故选:B
例6.(2022·全国·高二课时练习)若直线与曲线有两个交点,则实数的取值范围是( )
A. B.
C. D.
【答案】C
【解析】由题意,直线的方程可化为,所以直线恒过定点,,可化为其表示以为圆心,半径为2的圆的一部分,如图.
当与该曲线相切时,点到直线的距离,解得.
设,则.由图可得,若要使直线与曲线有两个交点,则.
故选:C.
例7.(2022·全国·高三专题练习)若直线y=x+b与曲线x恰有一个公共点,则b的取值范围是( )
A.﹣1<b≤1 B.﹣1≤b≤1
C.b≤﹣1 D.﹣1<b≤1或b
【答案】D
【解析】曲线x即 x2+y2=1(x≥0)表示一个半径为1的半圆,如图所示.
当直线y=x+b经过点A(0,1)时,求得b=1,
当直线y=x+b经过点B(1,0)时,求得b=﹣1,
当直线和半圆相切于点D时,由圆心O到直线y=x+b的距离等于半径,
可得1,求得b,或b(舍去).
故当直线y=x+b与曲线x恰有一个公共点时b的取值范围是﹣1<b≤1或b,
故选:D.
例8.(2022·全国·高三专题练习)若方程有两个不等的实根,则实数b的取值范围为( )
A. B. C. D.
【答案】B
【解析】由得,
所以直线与半圆有个公共点,
作出直线与半圆的图形,如图:
当直线经过点时,,
当直线与圆相切时,,解得或(舍),
由图可知,当直线与曲线有个公共点时,,
故选:B.
例9.(2022·全国·高三专题练习)已知直线与圆相交于,两点,则的值为( )
A. B.16 C. D.8
【答案】C
【解析】因为直线与圆相交于A,B两点,
所以,解得:.
所以.
故选:C.
例10.(2022·全国·高三专题练习)已知圆上仅有一点到直线的距离为1,则实数a的值为( ).
A.11 B. C.1 D.4
【答案】C
【解析】圆的标准方程是,圆心为,半径为,
圆心到直线的距离.
因为圆上仅有一点到直线的距离为1,
所以圆的半径,解得.
故选:C.
例11.(2022·全国·高三专题练习)如果圆上总存在两个点到原点的距离为,则实数的取值范围是( )
A. B.
C. D.
【答案】D
【解析】问题可转化为圆和圆相交,
两圆圆心距,
由得,
解得,即.
故选:D
例12.(2022·全国·高三专题练习)若直线 与圆 相交于 两点, 且 (其中 为原点), 则 的值为( )
A. 或 B. C. 或 D.
【答案】A
【解析】由可知,圆心到直线的距离为,根据点到直线的距离公式可得
故选:A
例13.(2022·全国·高三专题练习)已知直线过点且斜率为1,若圆上恰有3个点到的距离为1,则的值为( )
A. B. C. D.
【答案】D
【解析】直线过点且斜率为1,
设,
圆上恰有3个点到的距离为1,
圆心到直线的距离等于半径减去1,
圆心到直线的距离为,解得.
故选:D.
例14.(2022·全国·高二课时练习)若圆上存在四个点到直线的距离为,则实数m的取值范围是( )
A. B.
C. D.或
【答案】C
【解析】由题设,且半径,又圆上存在四个点到的距离为,
∴到的距离,可得.
故选:C
例15.(2022·江西·南昌大学附属中学高二期末(理))已知圆上有三个点到直线的距离等于1,则的值为( )
A. B. C. D.1
【答案】A
【解析】由圆可得圆心,半径,
因为圆上有三个点到直线的距离等于1,
所以圆心到直线的距离,
可得:,
故选:A.
例16.(2022·四川省绵阳南山中学高二阶段练习(文))已知直线:和圆:,且圆上至少存在两点到直线的距离为1,则的取值范围是( )
A. B.
C. D.
【答案】A
【解析】圆的方程为:,则圆心为,要使圆上至少存在两点到直线的距离为1,则当圆心到直线的距离必须小于3,即,解得.
故选:A
例17.(2022·全国·高二课时练习)若圆与轴、轴均有公共点,则实数的取值范围是______.
【答案】
【解析】圆的标准方程为,圆心坐标为,半径长为,
且该圆与轴、轴均有公共点,所以,,解得.
因此,实数的取值范围是.
故答案为:.
【方法技巧与总结】
直接联立求解.
题型三:切线与切线长问题
例18.(2022·全国·高三专题练习)已知圆:,为过的圆的切线,为上任一点,过作圆:的切线,则切线长的最小值是__________.
【答案】
【解析】由题,直线的斜率为,故直线的斜率为,故的方程为,即.又到的距离,故切线长的最小值是
故答案为:
例19.(2022·天津市武清区杨村第一中学模拟预测)由直线上的点向圆引切线(为切点),则线段的最小长度为________.
【答案】
【解析】圆的圆心,半径,点到直线的距离,
于是得,当且仅当垂直于直线时取“=“,
所以线段的最小长度为.
故答案为:
例20.(2022·云南玉溪·高二期末)已知直线经过点,且与圆相切,则的方程为( )
A. B. C. D.
【答案】A
【解析】直线经过点,且与圆相切,则,
故直线的方程为,即.
故选:A.
例21.(2022·辽宁·大连市一0三中学模拟预测)过点作圆的切线,则切线方程为( )
A. B. C. D.或
【答案】C
【解析】由圆心为,半径为,
斜率存在时,设切线为,则,可得,
所以,即,
斜率不存在时,显然不与圆相切;
综上,切线方程为.
故选:C
例22.(2022·全国·高三专题练习)已知圆.求满足下列条件的切线方程.
(1)过点;
(2)过点.
【解析】(1)因为圆的圆心为,半径为,点在圆上,
所以过点的切线斜率存在,且其与直线垂直,
因为,所以,所求切线的斜率为,
所以,所求切线方程为,即:.
(2)因为圆的圆心为,半径为,
所以,当过点的切线斜率不存在时,其方程为,满足题意;
当切线斜率存在时,设斜率为,则其方程为,即,
所以,圆心到切线的距离为,解得,
所以,切线方程为,即:.
综上,所求切线方程为或
例23.(2022·江苏连云港·模拟预测)直线与圆相切,则的值为( )
A. B.1 C. D.
【答案】C
【解析】因为直线与圆相切,
所以由圆心到直线的距离等于半径得:,即,解得:.
故选:C
例24.(多选题)(2022·全国·高二课时练习)过点作与圆相切的直线l,则直线l的方程为( )
A. B.
C. D.
【答案】BC
【解析】圆,即,则圆心为,半径为1,易知点在圆外,
显然是其中一条切线.
当切线斜率存在时,设切线方程为,则,解得,
所以切线方程为.综上,切线方程为或.
故选:BC.
例25.(多选题)(2022·全国·高二单元测试)设有一组圆Ck:,下列说法正确的是( )
A.这组圆的半径均为1
B.直线2x-y+2=0平分所有的圆Ck
C.存在无穷多条直线l被所有的圆Ck截得的弦长相等
D.存在一个圆Ck与x轴与y轴均相切
【答案】ABC
【解析】对于选项A:由圆Ck的方程可知,这组圆的半径均为1,故A正确;
对于选项B:圆Ck的圆心坐标为,因为2(k-1)-2k+2=0,所以直线2x-y+2=0过圆Ck的圆心,故B正确;
对于选项C:由B知,直线2x-y+2=0平分所有的圆Ck,所以存在无数条与直线2x-y+2=0平行或重合的直线(与直线2x-y+2=0的距离小于1)被所有的圆Ck截得的弦长相等,故C正确;
对于选项D:若圆Ck与x轴和y轴均相切,则,无解,故D错误.
故选:ABC.
【方法技巧与总结】
求圆的切线方程一般有三种方法:
(1)直接法:应用常见结论,直接写出切线方程;
(2)待定系数法;
(3)定义法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.
题型四:弦长问题
例26.(2022·安徽省太和中学高三阶段练习)在平面直角坐标系中,圆被直线截得的弦长2,则实数的值为___________.
【答案】
【解析】因为,所以圆心到直线的距离,所以,解得.
故答案为:
例27.(2022·河南·高三阶段练习(文))直线与圆C:相交于M,N两点,则______.
【答案】4
【解析】圆C:,其圆心坐标为,半径为3.
圆心到直线2x-y+1=0的距离,
则.
故答案为:4.
例28.(2022·全国·高二课时练习)设圆的圆心为C,直线l过,且与圆C交于A,B两点,若,则直线l的方程为___________.
【答案】或
【解析】当直线l的斜率不存在时,直线l的方程为,
由,得或,
此时,符合题意.
当直线l的斜率存在时,设直线,
因为圆的圆心,半径,
所以圆心C到直线l的距离.
因为,所以,解得,
所以直线l的方程为,即.
综上,直线l的方程为或.
故答案为:或
例29.(2022·全国·高三专题练习)在平面直角坐标系中,已知直线与圆交于A,B两点,若钝角的面积为,则实数a的值是______.
【答案】
【解析】由圆,即,
可得圆心坐标为,半径为,
因为钝角的面积为,可得,
解得,因为,所以,
可得,
设圆心到直线的距离为,又由圆的弦长公式,可得,解得,
根据点到直线的距离公式,解得.
故答案为:.
例30.(2022·全国·模拟预测)在平面直角坐标系xOy中,过点的直线l与圆相交于M,N两点,若,则直线l的斜率为__________.
【答案】
【解析】由题意得,直线的斜率存在,设,,直线MN的方程为,与联立,得,,得,,.因为,所以,则,于是,(由点A及C在y轴上可判断出,同号)
所以,两式消去,得,满足,所以.
故答案为:
例31.(2022·全国·高二专题练习)已知圆,直线l过点且与圆O交于A,B两点,当面积最大时,直线l的方程为_________.
【答案】
【解析】当直线l的斜率不存在时,直线l的方程为,
则由,得,所以
,
当直线l的斜率存在时,设直线l的方程为
原点到直线l的距离为:
当且仅当,即时取得等号.
由,解得
由
故直线l的方程为:,即
故答案为:
例32.(多选题)(2022·湖南·华容县教育科学研究室高一期末)已知动直线与圆,则下列说法正确的是( )
A.直线过定点
B.圆的圆心坐标为
C.直线与圆的相交弦的最小值为
D.直线与圆的相交弦的最大值为4
【答案】ACD
【解析】对于A,直线,即,
令,得,即直线过定点,故A正确;
对于B,圆,即,圆心坐标为,故B错误;
对于C,因为,所以直线所过定点在圆的内部,不妨设直线过定点为,
当直线与圆的相交弦的最小时,与相交弦垂直,
又因为,所以相交弦的最小为,故C正确;
对于D,直线与圆的相交弦的最大值为圆直径4,故D正确.
故选:ACD
例33.(多选题)(2022·全国·高二课时练习)若直线被圆所截得的弦长为,则实数a的值为( )
A.0 B.4 C. D.
【答案】AB
【解析】由圆的方程可知圆心坐标为,半径.
又直线被圆截得的弦长为,
所以圆心到直线的距离.
又,
所以,解得或.
故选:AB
例34.(多选题)(2022·河南·范县第一中学高二阶段练习)在平面直角坐标系中,O为坐标原点,已知圆O半径为3,直线l1、l2互相垂直,垂足为M(1,2),且l1与圆O相交于A、C两点,l2与圆O交于B、D两点,则四边形ABCD面积的值可以为( )
A.11 B.12 C.13 D.14
【答案】BC
【解析】如图,作于点,于点,
则,,则.
因为,所以,即,所以,故当时,有最大值26,此时,当或时,有最小值24,此时,所以四边形ABCD面积的范围为.
故选:BC
例35.(2022·全国·高二课时练习)若直线被圆截得的弦长不大于,求实数的取值范围.
【解析】圆的圆半径为,
设直线被圆截得的弦长为,圆心到直线的距离,
由题意,得,即,所以.
又,所以,所以或,
结合,可知或.
综上,实数的取值范围为.
【方法技巧与总结】
弦长问题
①利用垂径定理:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
②利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
③利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:.
题型五:判断圆与圆的位置关系
例36.(2022·全国·高二课时练习)已知圆和,则两圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
【答案】C
【解析】由题意,知圆的圆心,半径.
圆的方程可化为,则其圆心,半径.
因为两圆的圆心距,故两圆外切.
故选:C.
例37.(2022·全国·高三专题练习)已知两圆分别为圆和圆,这两圆的位置关系是( )
A.相离 B.相交 C.内切 D.外切
【答案】B
【解析】由题意得,圆圆心,半径为7;圆,圆心,半径为4,
两圆心之间的距离为,因为,故这两圆的位置关系是相交.
故选:B.
例38.(2022·陕西·铜川阳光中学高一期末)已知圆(,为常数)与.若圆心与圆心关于直线对称,则圆与的位置关系是( )
A.内含 B.相交 C.内切 D.相离
【答案】B
【解析】,,半径为,
关于直线的对称点为,即,所以,圆半径为,
,又,
所以两圆相交.
故选:B.
【方法技巧与总结】
已知两圆半径分别为,两圆的圆心距为,则:
(1)两圆外离;
(2)两圆外切;
(3)两圆相交;
(4)两圆内切;
(5)两圆内含;
题型六:由圆的位置关系确定参数
例39.(2022·云南省下关第一中学高三开学考试)若圆上总存在两个点到点的距离为2,则实数a的取值范围是( )
A. B.
C. D.
【答案】A
【解析】到点的距离为2的点在圆上,
所以问题等价于圆上总存在两个点也在圆上,
即两圆相交,故,
解得或,
所以实数a的取值范围为,
故选:A.
例40.(2022·湖北·荆门市龙泉中学二模)若点到直线的距离分别为1和4,则这样的直线共有( )条
A.4 B.3 C.2 D.1
【答案】C
【解析】到点距离为1的直线,可看作以为圆心1为半径的圆的切线,
同理到点距离为的直线,可看作以为圆心为半径的圆的切线,
故所求直线为两圆的公切线,
又,所以,故两圆相交,公切线有条,
故选:C.
例41.(2022·浙江·乐清市知临中学高二期中)已知,两点到直线的距离分别是2和3,则满足条件的直线共有( )条.
A.1 B.2 C.3 D.4
【答案】C
【解析】解析:分别以,为圆心,半径分别是2和3画圆,,两圆位置关系是外切,公切线有三条,
故选:C.
【点晴】此题的关键是发现直线和两点之间的关系,充分体现了数形结合思想的强大之处.
例42.(2022·全国·高三专题练习)已知圆和两点,,.若圆上存在点,使得,则的最小值为( )
A.7 B.6 C.5 D.4
【答案】D
【解析】
,点的轨迹是以为直径的圆,
又点在圆上,故点是圆与圆的交点,
因此可得两圆的位置关系是相切或相交,即,
解得:.
的最小值为4.
故选:D.
例43.(2022·山东聊城·二模)已知点在圆:上,点,,满足的点的个数为( )
A.3 B.2 C.1 D.0
【答案】B
【解析】设点,则,
且,由,得
,
即,
故点P的轨迹为一个圆心为、半径为的圆,
则两圆的圆心距为,半径和为,半径差为,
有,所以两圆相交,满足这样的点P有2个.
故选:B.
例44.(2022·全国·高三专题练习)若圆上存在点P,且点P关于直线y=x的对称点Q在圆上,则r的取值范围是( )
A. B. C. D.
【答案】A
【解析】根据题意,圆的圆心坐标为(0,1),半径为r,其关于直线y=x的对称圆的方程为,根据题意,圆与圆有交点,既可以是外切,也可以是相交,也可以是内切.
又圆,所以圆与圆的圆心距为,所以只需,解得.故B,C,D错误.
故选:A.
【方法技巧与总结】
利用几何法判定两圆的位置关系比用代数法(即解两圆方程联立方程组的方法)要简捷些,但需要注意的是,我们这里所说的几何法仍然是在解析几何前提下的几何法,即利用圆的方程及两点间距离公式求出两圆圆心距d和两圆的半径R和r,再根据d与、d与的大小关系来判定即可.
题型七:公共弦与切点弦问题
例45.(2022·广东·高三阶段练习)已知:,直线:,为直线上的动点,过点作的切线,,切点为,,当四边形的面积取最小值时,直线AB的方程为 ____.
【答案】
【解析】:的标准方程为,
则圆心,半径.
因为四边形的面积,
要使四边形面积最小,则需最小,此时与直线垂直,
直线的方程为,即,
联立,解得.则,
则以为直径的圆的方程为,
与的方程作差可得直线的方程为.
故答案为:.
例46.(2022·江苏·高二专题练习)已知圆的方程为,点是直线上的一个动点,过点作圆的两条切线、,、为切点,则四边形的面积的最小值为______
【答案】
【解析】由圆,得到圆心,半径
由题意可得:,,,
,
在中,由勾股定理可得:,
当最小时,最小,此时所求的面积也最小,
点是直线上的动点,
当时,有最小值,此时,
所求四边形的面积的最小值为;
故答案为:
例47.(2022·云南·昆明一中高三开学考试)已知圆和圆交于两点,则直线的方程是___________.
【答案】
【解析】由两圆相交,则交线的方程由两圆方程相减得到,
所以直线的方程是.
故答案为:
例48.(2022·全国·高三专题练习)圆与圆的公共弦长为______.
【答案】
【解析】设圆:与圆:交于,两点
把两圆方程相减,化简得
即:
圆心到直线的距离,又
而,所以
故答案为:
例49.(2022·全国·高三专题练习)已知圆:,点是直线上的动点,过作圆的两条切线,切点分别为,,则的最小值为( )
A. B. C. D.
【答案】B
【解析】圆:化为标准方程:,其圆心,半径.
过点P引圆C的两条切线,切点分别为点A、B,如图:
在△PAC中,有,即,变形可得:.
设,则.
所以当的值即x最小时,的值最大,此时最小.
而的最小值为点C到直线的距离,即,
所以.
故选:B
例50.(2022·全国·高三专题练习)已知圆,点M为直线上一个动点,过点M作圆C的两条切线,切点分别为A,B,则四边形周长的最小值为( )
A.8 B. C. D.
【答案】A
【解析】圆的圆心坐标为,半径为,
因为过点M作圆C的两条切线,切点分别为A,B,
所以有,,
因此有,
要想四边形周长最小,只需最小,即当时,
此时,此时,
即最小值为,
故选:A
例51.(2022·全国·高二课时练习)已知点P为直线上的动点,过点P作圆的两条切线,切点分别为A B,则直线必过定点( )
A. B. C. D.
【答案】A
【解析】设,
圆的圆心为,一般方程为①,
线段中点坐标为,
,
所以以线段为直径的圆的方程为,
整理得②,
①-②并化简得,
即,
.
所以定点坐标为.
故选:A
例52.(2022·安徽·屯溪一中高二期中)已知直线是圆的对称轴.过点作圆的两条切线,切点分别为、,则直线的方程为( )
A. B. C. D.
【答案】A
【解析】根据题意,圆C的标准方程为,即圆心为 C(2,1),半径为2.
点(2,1)在直线上,即
点A的坐标为(-4,-1)
过点A作圆C的切线所得切线长为
以点A为圆心,6为半径的圆A的方程为
圆A与圆C的方程作差得,即直线BD的方程为
故选:A.
例53.(2022·四川省绵阳第一中学高二期中)过点作圆C:的两条切线,切点分别为A,B,则直线AB的方程为( )
A. B. C. D.
【答案】A
【解析】,即,圆心为,半径.
当斜率不存在时,直线与圆相切,切点为;
当斜率为0时,直线与圆相切,切点为.
故直线方程为斜率,直线方程为,即.
故选:A.
例54.(2022·江苏常州·一模)过圆:外一点作圆的切线,切点分别为、,则( )
A.2 B. C. D.3
【答案】C
【解析】如图,结合题意绘出图像:
因为圆:,直线、是圆的切线,
所以,,,,
因为,所以,,
根据圆的对称性易知,则,
解得,,
故选:C.
例55.(2022·江苏·高二专题练习)已知圆M:,直线l:,P为直线l上的动点,过P点作圆M的切线PA、PB,切点为A、B,当最小时,直线AB的方程为( )
A. B.
C. D.
【答案】A
【解析】因为圆,即为,
所以圆心,半径.
.
要使最小,则需最小,此时PM与直线l垂直.
直线PM的方程为,即,
联立,解得,即.
则以PM为直径的圆O的方程为.
直线AB为圆M与圆O公共弦所在直线,
联立
相减可得直线AB的方程为.
故选:A.
例56.(多选题)(2022·全国·高二课时练习)圆和圆的交点为A,B,则有( )
A.公共弦AB所在直线的方程为
B.公共弦AB所在直线的方程为
C.公共弦AB的长为
D.P为圆上一动点,则P到直线AB距离的最大值为
【答案】AD
【解析】由与作差可得,
即公共弦AB所在直线的方程为,故A正确,B错误;
对于C,圆心到直线的距离为,圆的半径,
所以,故C错误;
对于D,点P为圆上一动点,则点P到直线AB距离的最大值为,故D正确.
故选:AD.
例57.(2022·广东·汕头市潮阳区棉城中学高二期中)过直线上任意点作圆的两条切线,切点分别为,当切线长最小时,切线长为_________;同时 的面积为_______.
【答案】 1
【解析】依据题意,作出图形,如下图:
因为直线过点且与圆相切于点A,
所以,所以,
要使得最小,则要最小,
由题可得:的最小值就是点到直线的距离.
此时,,所以
由切线的对称性可得:
所以的面积为,
故答案为:1;.
例58.(2022·浙江绍兴·模拟预测)已知圆C的方程为,则圆心C的坐标为___________,圆C与圆D:的公共弦所在直线方程为___________.
【答案】
【解析】因为圆C的方程为,即,
故圆心C的坐标为;
由于圆D:,两圆方程相减可得,
即公共弦所在直线方程为,
故答案为:,.
【方法技巧与总结】
(1)圆的切线方程的求法
①点在圆上,
法一:利用切线的斜率与圆心和该点连线的斜率的乘积等于,即.
法二:圆心到直线的距离等于半径.
②点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
注意:因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
(2)常见圆的切线方程
过圆上一点的切线方程是;
过圆上一点的切线方程是.
过圆外一点作圆的两条切线,则两切点所在直线方程为
过曲线上,做曲线的切线,只需把替换为,替换为,替换为,替换为即可,因此可得到上面的结论.
(3)两圆的公共弦方程为两圆方程相减可得.
题型八:公切线问题
例59.(2022·广东·中山一中高三阶段练习)已知圆.若圆与圆有三条公切线,则的值为___________.
【答案】
【解析】由,得,
所以圆的圆心为,半径为,
因为圆,所以圆的圆心为,半径为,
因为圆与圆有三条公切线,所以圆与圆相外切,
即,解得,
所以的值为.
故答案为:.
例60.(2022·广东广州·高二期末)写出与圆和圆都相切的一条切线方程___________.
【答案】或或
【解析】圆的圆心为,半径为1;圆的圆心为,半径为4,
圆心距为,所以两圆外切,如图,有三条切线,
易得切线的方程为,
因为,且,所以,设,即,
则到的距离,解得(舍去)或,所以,
可知和关于对称,联立,解得在上,
在上任取一点,设其关于的对称点为,
则,解得,
则,所以直线,即,
综上,切线方程为或或.
故答案为:或或.
例61.(多选题)(2022·全国·高二课时练习)已知圆,圆,则下列是M,N两圆公切线的直线方程为( )
A.y=0 B.3x-4y=0 C. D.
【答案】ACD
【解析】圆M的圆心为M(2,1),半径.圆N的圆心为N(-2,-1),半径.圆心距,两圆相离,故有四条公切线.又两圆关于原点O对称,则有两条切线过原点O,设切线方程为y=kx,则圆心到直线的距离,解得k=0或,对应方程分别为y=0,4x-3y=0.另两条切线与直线MN平行,而,设切线方程为,则,解得,切线方程为,.
故选:ACD.
例62.(2022·全国·高二专题练习)若直线与圆,圆都相切,切点分别为、,则( )
A. B. C. D.
【答案】C
【解析】如下图所示,设直线交轴于点,
由于直线与圆,圆都相切,切点分别为、,
则,,,
,为的中点,为的中点,,
由勾股定理可得.
故选:C.
例63.(2022·全国·高二单元测试)已知点M,N分别在圆与圆上,则的最大值为( )
A. B.17 C. D.15
【答案】C
【解析】圆的圆心,半径,圆的圆心,半径,
则.
故选:C
例64.(多选题)(2022·全国·高二课时练习)若直线与圆相切,则直线与圆的位置关系可能是( )
A.相交 B.相切 C.相离 D.不确定
【答案】AC
【解析】由圆C的方程知其圆心C(2,1),半径为.
因为直线l与圆C相切,所以,解得.
由圆D的方程知其圆心D(2,0),半径,圆心D到直线l的距离.
当时,,即,此时直线l与圆D相离;
当时,,即,此时直线l与圆D相交.
综上所述,直线l与圆D相交或相离.
故选:AC.
例65.(2022·全国·高三专题练习)在平面直角坐标系中,圆:与圆:,则两圆的公切线的条数是( )
A.4条 B.3条 C.2条 D.1条
【答案】A
【解析】圆:的圆心,半径,
圆:的圆心,半径,
,显然,即圆与圆外离,
所以两圆的公切线的条数是4.
故选:A
例66.(2022·全国·高三专题练习)已知圆,圆,则同时与圆和圆相切的直线有( )
A.4条 B.2条 C.1条 D.0条
【答案】B
【解析】由,得圆,半径为,
由,得,半径为
所以,
,,
所以,所以圆与圆相交,
所以圆与圆有两条公共的切线.
故选:B.
例67.(2022·全国·高二课时练习)求圆与圆的公切线所在直线的方程.
【解析】由题意得,圆心为,半径,,圆心为,半径,
可知两圆的公切线所在直线的斜率存在,
设公切线所在直线的方程为,即
由,得,得或,
当时,,解得或,
当时,,解得或,
综上,两圆的公切线所在直线的方程为,,,.
例68.(2022·全国·高二专题练习)求圆与圆的内公切线所在直线方程及内公切线的长.
【解析】,,,.
设内公切线与连心线交于点,则在轴上且.
设,可得,.
设内公切线所在直线方程为,即.
由,得.
所以内公切线所在直线方程为或.
内公切线的长为.
【方法技巧与总结】
利用几何法进行转化.
题型九:圆中范围与最值问题
例69.(2022·江苏·高二专题练习)已知 ,且动点满足,则取得最小值时,点的坐标是___________.
【答案】
【解析】设,则,整理可得:;
,
当三点共线且在线段上时,取得最小值,
又直线方程为:,即,
由得:或,
又在线段上,.
故答案为:.
例70.(2022·全国·模拟预测)已知直线与圆交于不同的两点,,点,则的最大值为______.
【答案】
【解析】解 由,得.
设,,则,,
因为,所以
.
令,则,,
所以
,
当且仅当时等号成立.
所以的最大值为.
故答案为:.
例71.(2022·重庆一中高一期末)直线分别与x轴 y轴相交于A B两点,点P在圆上运动,则面积的最小值为___________.
【答案】2
【解析】直线分别与轴,轴交于,两点,
,,则,
点在圆上,
圆心为,则圆心到直线距离,
故点到直线的距离的范围为,
则.
的最小值为.
故答案为:.
例72.(2022·全国·高二课时练习)若点M为圆上任意一点,直线过定点P,则的最大值为______.
【答案】
【解析】整理直线方程得,
由,得,所以.
由圆的方程知圆心,半径,
所以.
故答案为:
例73.(2022·上海市控江中学高二期末)已知点在圆上运动,则的最大值为( )
A. B. C. D.
【答案】C
【解析】看作圆上的点到点的直线的斜率的相反数.
当经过点的直线与上半圆相切时,切线斜率最小,
设切线方程为,所以圆心到切线的距离等于半径,故,解得 故当时,切线斜率最小,此时最大,最大值为,
故选:C
例74.(2022·河南·修武一中高二开学考试(理))已知直线与圆交于两点,过分别作的垂线与轴交于两点,则当最小时,( )
A.4 B. C.8 D.
【答案】D
【解析】直线过定点,最小时,,
圆心到直线的距离,,
因为,所以此时,所以直线的倾斜角为,
过点作交于点,则,
在中,所以.
故选:D
例75.(2022·广东·佛山一中高二期中)已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形面积为( )
A. B. C. D.
【答案】C
【解析】圆的标准方程为,圆心为,半径为,
,故点在圆内,如下图所示:
则,
过点的弦过圆心时,弦长取最大值,即,
当过的弦与垂直时,弦长取最小值,即,此时,
此时,四边形的面积为.
故选:C.
例76.(2022·全国·高三专题练习)当圆的圆心到直线的距离最大时,( )
A. B. C. D.
【答案】C
【解析】因为圆的圆心为,半径,
又因为直线过定点A(-1,1),
故当与直线垂直时,圆心到直线的距离最大,
此时有,即,解得.
故选:C.
例77.(2022·全国·高二专题练习)已知圆上的点到直线的距离等于,那么的值不可以是( )
A. B. C. D.
【答案】D
【解析】直线过定点,因为,故点在圆外,
圆心,半径为,且,
所以,圆心到直线的距离的最大值为,
所以,圆上的到直线的距离的最大值为,
当直线有公共点时,圆上的到直线的距离的最小值为,
故圆上的点到直线的距离的取值范围是,
且、、,.
故选:D.
例78.(多选题)(2022·江苏·高二专题练习)圆C方程:,P为圆上的动点,则下列说法错误的是( )
A.的最大值为
B.P点到A点距离的最小值为
C.的最大值为
D.圆C的内接正三角形的面积为
【答案】BD
【解析】因为圆C方程:,
所以,圆心,半径为1,
设,当与相切时,有最值,
,,
所以的最大值为,选项A正确;
P点到A点距离的最小值为,选项B错误;
因为表示的几何意义为圆上的点与定点连线的斜率,
设,即,所以直线与圆C相切时,k有最值,
当直线与圆相切时,有,所以,
所以的最大值为,所以C选项正确;
因为圆的半径为1,所以圆C的内接正三角形的边长为,所以圆C的内接正三角形的面积为,选项D错误;
故选:BD.
例79.(2022·全国·高二课时练习)已知圆.
(1)直线过点,且与圆C相切,求直线的方程;
(2)设直线与圆C相交于M,N两点,点P为圆C上的一动点,求的面积S的最大值.
【解析】(1)由题意得C(2,0),圆C的半径为3.
当直线的斜率存在时,设直线的方程为y-l=k(x+1),即kx-y+k+1=0,
由直线与圆C相切,得,解得,所以直线的方程为4x-3y+7=0.
当直线的斜率不存在时,直线的方程为,显然与圆C相切.
综上,直线的方程为x=-1或4x-3y+7=0.
(2)由题意得圆心C到直线的距离,
设圆C的半径为r,所以r=3,所以,
点P到直线距离的最大值为,
则的面积的最大值.
【方法技巧与总结】
涉及与圆有关的最值,可借助图形性质,利用数形结合求解.一般地:
(1)形如的最值问题,可转化为动直线斜率的最值问题.
(2)形如的最值问题,可转化为动直线截距的最值问题.
(3)形如的最值问题,可转化为曲线上的点到点(a,b)的距离平方的最值问题
题型十:圆系问题
例80.(2022·全国·高二专题练习)求经过圆与直线的交点且在轴上的弦长为的圆的方程.
【解析】设所求的圆的方程为,且与轴的交点坐标为,
令得,化简得
,
由两边平方得
,化简得
解得或
所求圆的方程为,
或
所求圆的方程为或
例81.(2022·江苏·高二专题练习)已知圆:与:相交于A、B两点.
(1)求公共弦AB所在的直线方程;
(2)求圆心在直线y=-x上,且经过A、B两点的圆的方程;
(3)求经过A、B两点且面积最小的圆的方程.
【解析】(1)将两圆方程相减得x-2y+4=0,此即为所求直线方程.
(2)设经过A、B两点的圆的方程为(为常数),
则圆心坐标为;又圆心在直线y=-x上,故,
解得,故所求方程为.
(3)由题意可知以线段AB为直径的圆面积最小.两圆心所在直线方程为2x+y+3=0,
与直线AB方程联立得所求圆心坐标为,由弦长公式可知所求圆的半径为.
故面积最小的圆的方程为.
例82.过圆与的交点,且圆心在直线上的圆的方程是_______.
【答案】
【解析】
设圆的方程为,
则,
即,所以圆心坐标为,
把圆心坐标代入,可得,
所以所求圆的方程为.
故答案为:.
例83.已知圆与圆相交于A、B两点.
(1)求公共弦AB所在直线方程;
(2)求过两圆交点A、B,且过原点的圆的方程.
【解析】(1),①
,②
①-②得
即公共弦AB所在直线方程为.
(2)设圆的方程为
即
因为圆过原点,所以,
所以圆的方程为
【方法技巧与总结】
圆系方程:若圆与圆相交于A,B两点,则过A,B两点的圆系方程为:
简记为:,不含
当时,该圆系退化为公共弦所在直线(根轴)
注意:与圆C共根轴l的圆系
【同步练习】
一、单选题
1.设圆,圆,则圆,的公切线有( )
A.1条 B.2条 C.3条 D.4条
【答案】B
【解析】由题意,得圆,圆心,圆,圆心,∴,∴与相交,有2条公切线.
故选:B.
2.求与直线平行且将圆的周长平分的直线方程为( )
A. B.
C. D.
【答案】C
【解析】圆的圆心坐标,
所求直线将圆平分,
则直线过圆的圆心,
又因为与直线平行,则所求直线的斜率为,
利用点斜式得到直线方程为,整理成一般式为
故选:C
3.直线绕原点按逆时针方向旋转后所得的直线l与圆的位置关系是( )
A.直线l过圆心 B.直线l与圆相交,但不过圆心
C.直线l与圆相切 D.直线l与圆无公共点
【答案】C
【解析】直线过原点,斜率为,倾斜角为,依题意,直线l的倾斜角为,斜率为,而l过原点,
因此,直线l的方程为:,又圆的圆心为,半径为,
于是得点到直线l的距离为,所以直线l与圆相切.
故选:C
4.设是圆上的动点,是圆的切线,且,则点到点距离的最小值为( )
A.4 B.5 C.6 D.15
【答案】B
【解析】由圆,可知圆心,半径为3,又,
所以,即点的轨迹方程为,
故点到点距离的最小值为.
故选:B.
5.已知直线l:与圆O:相交于不同的两点A,B,若∠AOB为锐角,则m的取值范围为( )
A. B.
C. D.
【答案】A
【解析】因为直线l:经过定点,圆O:的半径为,
当∠AOB为直角时,此时圆心O到直线l的距离,解得,
则当∠AOB为锐角时,.
又直线与圆相交于A,B两点,则,即,
所以或,
故选:A.
6.若点C到的距离之比为,则点C到直线的距离的最小值为( )
A. B. C. D.
【答案】A
【解析】设,则,即,化简得,
所以点的轨迹为以为圆心,的圆,
则圆心到直线的距离,
所以点C到直线的距离的最小值为;
故选:A.
7.古希腊数学家阿波罗尼斯(约前262—前190年)的著作《圆锥曲线论》是古代光辉的科学成果,著作中有这样一个命题:平面内与两定点距离的比为常数且的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.已知,,圆上有且仅有一个点P满足,则r的取值为( )
A.1 B.5 C.1或5 D.不存在
【答案】C
【解析】设点P
∵即
整理得:
∴点P的轨迹为以为圆心,半径的圆,
∵圆的为圆心,半径的圆
由题意可得:或
∴或
故选:C.
8.从空中某个角度俯视北京冬奥会主体育场“鸟巢”顶棚所得的局部示意图如图,在平面直角坐标系中,下列直线系方程(其中为参数,)能形成这种效果的是( )
A. B.
C. D.
【答案】C
【解析】由图可知,原点到直线的距离为定值,四个选项中仅有到原点的距离为定值.
故选:C
二、多选题
9.已知圆与圆有四条公切线,则实数a的取值可能是( )
A.-4 B.-2 C. D.3
【答案】AD
【解析】圆心,半径,圆心,半径.因为两圆有四条公切线,所以两圆外离.又两圆圆心距,所以,解得或.
故选:AD.
10.已知圆C:,则下列四个命题表述正确的是( )
A.圆C上有且仅有3个点到直线1:的距离都等于1
B.过点作圆C的两条切线,切点分别为M,N,直线MN的方程为
C.一条直线与圆C交于不同的两点P,Q,且有,则∠PCQ的最大值为
D.若圆C与E:相外切,则
【答案】BC
【解析】圆C的圆心,半径,
圆心到直线l:的距离,故圆C上有4个点到直线l的距离为1,故A不正确;
过点作圆C的两条切线,切点分别为M,N,则A、C、M、N四点共圆,且为AC为直径,方程为,MN是其圆C的公共弦,直线MN为,故B正确;
设PQ的中点为D,则.因为,
即,可得,
则,故的最大值为,故C正确;
圆E:的圆心,半径
根据题意可得,即得,故D错误.
故选:BC.
11.已知M为圆C:上的动点,P为直线l:上的动点,则下列结论正确的是( )
A.直线l与圆C相切 B.直线l与圆C相离
C.|PM|的最大值为 D.|PM|的最小值为
【答案】BD
【解析】圆C:得圆心,半径
∵圆心到直线l:得距离
∴直线l与圆C相离
A不正确,B正确;
C不正确,D正确;
故选:BD.
12.若实数x,y满足,则下列说法正确的是( )
A.x的最小值是4
B.x的最大值是20
C.若关于y的方程有一解,则x的取值范围为
D.若关于y的方程有两解,则x的取值范围为
【答案】BD
【解析】当时,解得,符合题意;当时,令,则,又,则,即,则原方程可化为.设,,,则的图象是斜率为的直线的一部分,的图象是以原点为圆心,半径为的四分之一圆,则问题等价于的图象和的图象有公共点,观察图形可知,
当直线与圆相切时,由,解得;当直线过点时,,解得;当直线过点时,,解得.因此,要使直线与圆有公共点,则有,综上,,故x的最大值为20,最小值为0.显然当或或时,y有一解;当时,y有两解.
故选:BD.
三、填空题
13.大约在2000多年前,我国的墨子给出了圆的概念“一中同长也”,意思是说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下定义要早100多年.已知直角坐标平面内有一点和一动点满足,若过点的直线将动点的轨迹分成两段弧,当劣弧所对的圆心角最小时,直线的斜率__________.
【答案】
【解析】依题意可知,动点的轨迹是以为圆心,为半径的圆,
即.
因为,故点在内.
当劣弧所对的圆心角最小时,.
因为直线的斜率,
所以所求直线的斜率.
故答案为:.
14.规定:在桌面上,用母球击打目标球,使目标球运动,球的位置是指球心的位置,球是指该球的球心点.两球碰撞后,目标球在两球的球心所确定的直线上运动,目标球的运动方向是指目标球被母球击打时,母球球心所指向目标球球心的方向.所有的球都简化为平面上半径为1的圆,且母球与目标球有公共点时,目标球就开始运动,在桌面上建立平面直角坐标系,如图,设母球的位置为(0,0),目标球的位置为,要使目标球向处运动,则母球的球心运动的直线方程为______.
【答案】
【解析】点,所在直线的方程为,如图所示
可知,两球碰撞时,球的球心在直线上,且在第一象限,设,两球碰撞时,球的球心坐标为,此时,则,解得,即,B两球碰撞时,球的球心坐标
所以母球的球心运动的直线方程为,即.
故答案为:
15.直线与半圆有两个交点,则的值是____.
【答案】
【解析】由半圆,即,
如图所示,当直线在第三象限与半圆相切时,圆心到直线的距离,
即,解得:或(舍去),
当直线过点时,直线与圆有两个交点和,
把代入中,可得 ,解得,
则直线与圆有两个交点时,的范围是.
故答案为:
16.设直线系,对于下列四个命题:
①M中所有直线均经过一个定点;
②存在定点P不在M中的任一条直线上;
③对于任意整数,存在正n边形,使其所有边均在M中的直线上;
④M中的直线所能围成的正三角形面积都相等.
其中真命题的序号是_________(写出所有真命题的序号)
【答案】②③
【解析】由直线系,
可令,消去可得,
故直线系表示圆的切线的集合,故①不正确;
因为对任意,存在定点不在直线系中的任意一条上,故②正确;
由于圆的外切正边形,所有的边都在直线系中,故③正确;
中的直线所能围成的正三角形的边长不一定相等,故它们的面积不一定相等,如图中等边三角形和面积不相等,故④不正确.
综上,正确的命题是②③.
故答案为:②③.
四、解答题
17.从①与直线4x-3y+5=0垂直,②过点(5,-5),③与直线3x+4y+2=0平行这三个条件中任选一个,补充在下面的问题中,并加以解答.
问题:已知直线l过点,且______.
(1)求直线l的一般式方程;
(2)若直线l与圆相交于点P,Q,求弦PQ的长.
注:如果选择多个条件分别解答,按第一个解答计分.
【解析】(1)方案一:选条件①.
(1)因为直线4x-3y+5=0的斜率为,且与直线l垂直,所以直线l的斜率为,
依题意,直线l的方程为,即3x+4y+5=0.
方案二:选条件②.
(1)因为直线l过点(5,-5)及(1,-2),
所以直线l的方程为,即.
方案三:选条件③.
(1)因为直线3x+4y+2=0的斜率为,直线l与直线3x+4y+2=0平行,
所以直线l的斜率为.
依题意,直线l的方程为,即3x+4y+5=0.
(2)方案一:选条件①.
(2)圆的圆心(0,0)到直线3x+4y+5=0的距离为.
又圆的半径为,所以.
方案二:选条件②.
(2)解析同方案一中(2).
方案三:选条件③.
(2)解析同方案一中(2).
18.在①,②最小,③过A,B两点分别作圆C的切线,切线交于点P(2,0)这三个条件中任选一个,补充在下面问题中,并求解.
在平面直角坐标系中,已知圆,直线l过定点M(1,1).设直线l与圆C交于A,B两点,当______时,求直线l的方程.
【解析】将圆的方程化为,则C(0,2),半径r=2.
方案一:选条件①.
因为,所以,所以.
当直线l的斜率不存在时,方程为x=1,此时,不符合题意.
当直线l的斜率存在时,设方程为,即,
由题意可知,即,解得k=1,所以直线.
方案二:选条件②.
当直线所过定点M(1,1)为弦AB的中点时,最小,此时,,所以直线l的斜率为1,所以直线.
方案三:选条件③.
因为过A,B两点分别作圆C的切线,切线交于P(2,0),所以,,所以直线l的斜率为1,又直线过定点M(1,1),所以直线.
19.已知圆,平面上一动点P满足:且,.
(1)求动点P的轨迹方程;
(2)过点N的直线l(斜率为正)交圆G于A C两点,交P的轨迹于B D两点(A B在第一象限),若,求直线l的方程.
【解析】(1)设,则,
整理得:.
(2)由题知l斜率为正,设直线,
则原点到直线l的距离为:,
故,
又圆,所以圆心,半径为2,
所以G到直线l的距离为:,
故,
又,所以,
所以,
整理得:,
解得:,(舍负),
所以直线l的方程为:.
20.已知直线过定点,且与圆交于、两点.
(1)求直线的斜率的取值范围.
(2)若为坐标原点,直线、的斜率分别为、,试问是否为定值?若是,求出该定值;若不是,请说明理由.
【解析】(1)圆的标准方程为,圆心为,半径为.
若直线的斜率不存在,此时直线与圆相切,不合乎题意.
所以,直线的斜率存在,设直线的方程为,
由题意可得,解得.
因此,直线的斜率的取值范围是.
(2)设,,设直线的方程为.
联立,得,其中,
所以,,
则,
所以为定值.
21.在平面直角坐标系中,光线过点,经轴反射后与圆:有交点
(1)当反射后光线经过圆心,求光线的方程;
(2)当反射后光线与圆相切,求光线的方程.
【解析】(1)点关于轴对称的点为,由光线的折射性质,反射光线经过圆心,所以,
易知,所以,
所以光线的方程为.
(2)设经过的直线方程为由于折射光线与圆相切,
所以圆心到直线的距离等于半径,即,
化简得:,
解得或,
所光线的方程为或.
22.如图,在平面直角坐标系上,已知圆的直径,定直线到圆心的距离为,且直线垂直于直线,点是圆上异于、的任意一点,直线、分别交与、两点.
(1)求过点且与圆相切的直线方程;
(2)若,求以为直径的圆方程;
(3)当点变化时,以为直径的圆是否过圆内的一定点,若过定点,请求出定点;若不过定点,请说明理由.
【解析】(1)易知圆的方程为,圆心为原点,半径为,
若所求直线的斜率不存在,则所求直线的方程为,此时直线与圆相切,合乎题意,
若所求直线的斜率存在,设所求直线的方程为,即,
由已知可得,解得,此时所求直线的方程为.
综上所述,过点且与圆相切的直线方程为或.
(2)易知直线的方程为,、,
若点在轴上方,则直线的方程为,
在直线的方程中,令,可得,即点,
直线的方程为,
在直线的方程中,令,可得,即点,
线段的中点为,且,此时,所求圆的方程为;
若点在轴下方,同理可求得所求圆的方程为.
综上所述,以为直径的圆方程为.
(3)不妨设直线的方程为,其中,
在直线的方程中,令,可得,即点,
因为,则直线的方程为,
在直线的方程中,令,可得,即点,
线段的中点为,,
所以,以线段为直径的圆的方程为,
即,由,解得,
因此,当点变化时,以为直径的圆是否过圆内的定点
