2022-2023学年沪科版七年级数学上册 4.5角的比较 课件(共27张PPT)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学上册 4.5角的比较 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 399.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 09:03:07 | ||
图片预览





文档简介
(共27张PPT)
1.什么是角?
复习回顾
从一点发出的两条射线所组成的图形叫做角
一条射线绕着端点旋转一定的角度所组成的图形叫做角
静态定义:
动态定义:
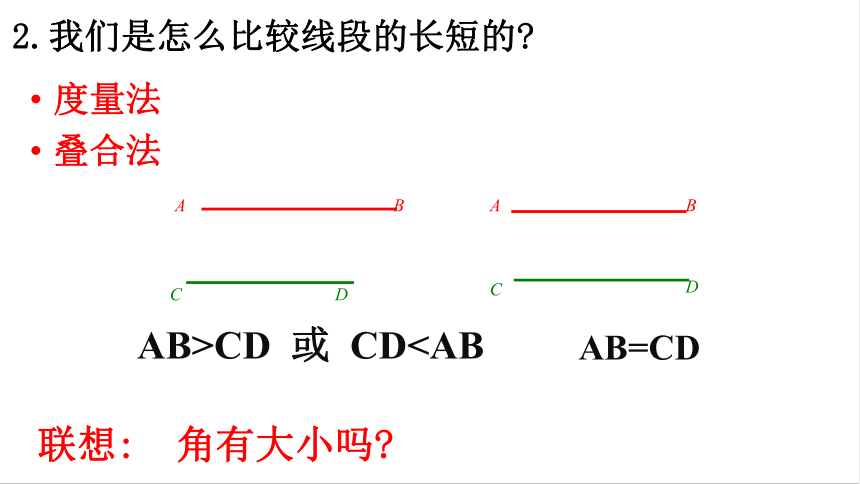
2.我们是怎么比较线段的长短的
度量法
叠合法
A
B
C
D
AB>CD 或 CD联想: 角有大小吗
A
B
C
D
AB=CD
4.5角的比较与补(余)角
第一课时
学习目标
1.会比较角的大小,理解两个角的和、差、倍、分的意义.(重点)
2.了解角平分线的概念,会进行相关的计算.(难点)
请同学们任意画一个∠AOB,
并量出它的度数。
1、度量法
C
A
B
O
30
0
60
90
120
150
180
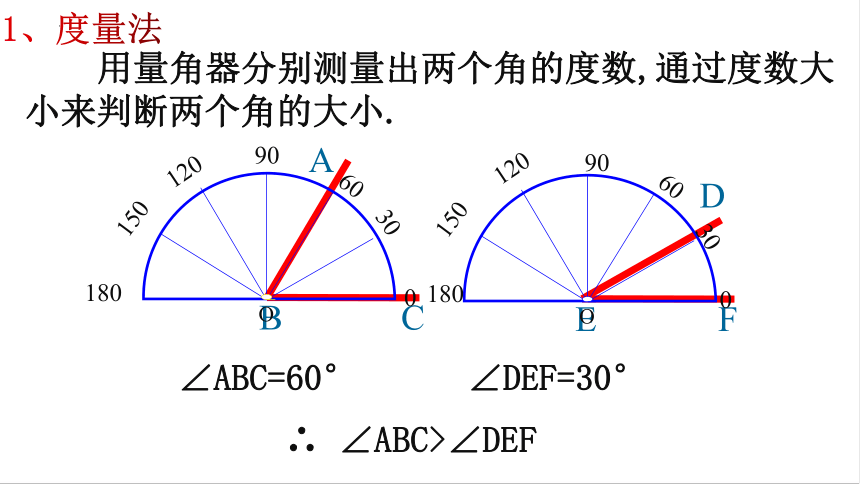
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴ ∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
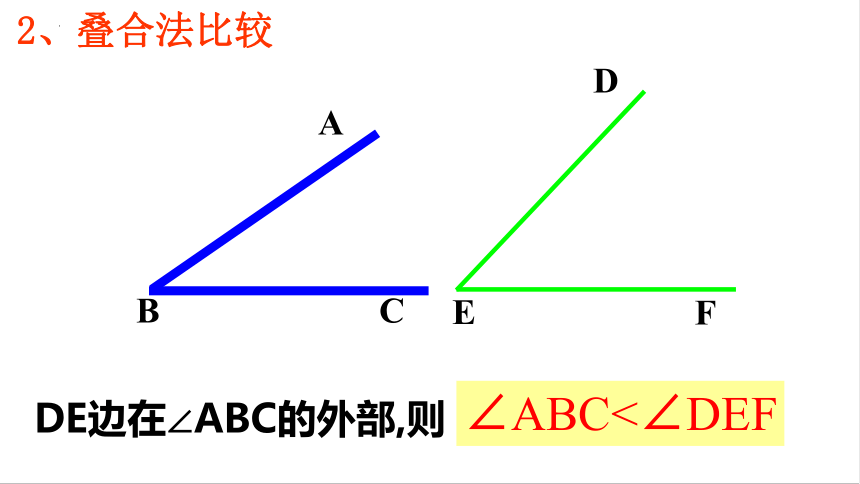
2、叠合法
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
B
A
C
E
D
F
∠ABC<∠DEF
B
C
A
E
D
F
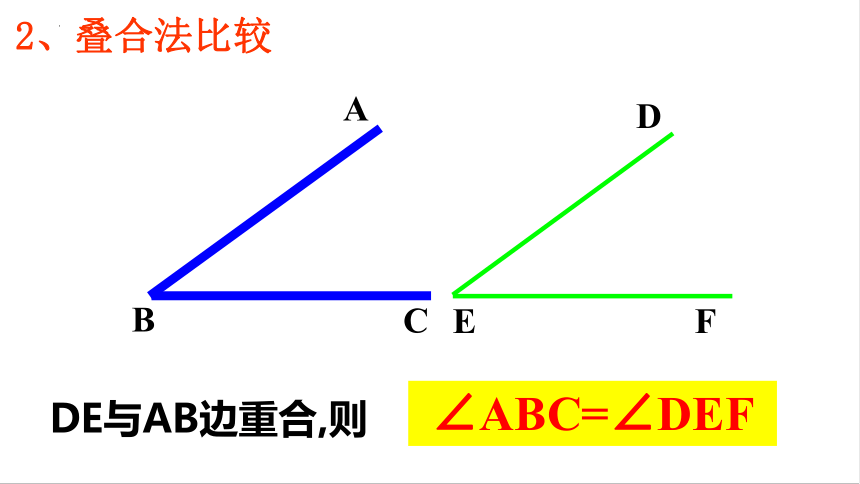
2、叠合法比较
DE边在∠ABC的外部,则
∠ABC=∠DEF
B
A
C
E
D
F
DE与AB边重合,则
2、叠合法比较
∠ABC>∠DEF
B
A
C
D
E
F
DE边在∠ABC的内部,则
2、叠合法比较
∠ABC=∠DEF
∠ABC<∠DEF
∠ABC>∠DEF
(F)
B
(E)
A
C
(D)
C
B
(E)
A
D
(F)
D
B
(E)
(F)
C
A
2、叠合法比较
说明:
1、两角的顶点必须重合;
2、一边必须重合,另一边落在重合的一边的同侧.
1.角的大小与两边画出部分的长短是否相关?
2.一个30°的角用能放大3倍的放大镜观看,看到的角度有何变化?
仪一仪
A
C
B
O
图中共有几个角?它们之间有什么关系?
二、角的和与差:
图中∠AOC是∠AOB和∠BOC的和,记作:∠AOC=∠AOB+∠BOC
图中∠AOB是∠AOC和∠BOC的差,
记作:∠AOB=∠AOC-∠BOC
那么,图中∠AOC-∠AOB=
∠BOC
认识角的和差
例1 如图,求解下列问题:
(1)试比较∠AOC与∠BOC的大小,∠BOD与∠COD的大小;
(2)将∠AOC写成两个角的和与两个角的差的式.
解:(1)由图可看出:∠AOC>∠BOC,(OB在∠AOC内); ∠BOD>∠COD.(OC在∠B内)
O
A
B
C
D
A
B
C
D
(2)∠AOC=∠AOB+∠BOC;
∠AOC=∠AOD-∠DOC.
O
如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
填一填:
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线(angular bisector)
O
A
B
C
定义:
上图中,∠AOC、∠BOC与∠AOB之间有怎么样的大小关系?它们之间的关系可以怎么表示?
角的平分线:
若OC平分∠AOB,
则∠AOC=∠BOC= ∠AOB ;
或∠AOB=2∠AOC=2∠BOC.
A
B
O
c
几何语言:
例2:如图,∠ABC=90°,∠CBD=30°,BP平分∠ABD. 求∠ABP的度数.
A
B
C
D
P
2. 如图,∠ABC=60°,∠ABD=145°,BE平分∠ABC,求∠DBE的度数
A
B
C
D
E
解: ∵ ∠ABC=60°,∠ABD=145°
∠ABD- ∠ABC
= 145°- 60°=85°
又∵ BE平分∠ABC
∴ ∠CBE= ∠ABC= × 60°= 30°
∠CBD+∠CBE
= 85°+ 30°=115°
∴ ∠CBD=
∴ ∠DBE=
1.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
25
当堂练习
2.如图,∠1=∠3,那么( ).
A.∠1=∠2 B. ∠2=∠3
C.∠AOC=∠BOD D. ∠1=
C
3.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD等于( )
A.30° B.35°
C.20° D.40°
B
4.如图,点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
5.已知射线OA,若从点O引两条射线OB和OC,使∠AOB=50°,∠BOC=20°,求∠AOC的度数.
谈谈这节课的收获……
还有什么困惑……
利用一副三角板,我们能画出哪些度数的角?
探究活动
180
15
135
150
75
105
60
30
45
120
15 ,30 ,45 ,60 ,75 ,90 ,105 ,120 ,135 ,150 ,180 等
1.什么是角?
复习回顾
从一点发出的两条射线所组成的图形叫做角
一条射线绕着端点旋转一定的角度所组成的图形叫做角
静态定义:
动态定义:
2.我们是怎么比较线段的长短的
度量法
叠合法
A
B
C
D
AB>CD 或 CD
A
B
C
D
AB=CD
4.5角的比较与补(余)角
第一课时
学习目标
1.会比较角的大小,理解两个角的和、差、倍、分的意义.(重点)
2.了解角平分线的概念,会进行相关的计算.(难点)
请同学们任意画一个∠AOB,
并量出它的度数。
1、度量法
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴ ∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
2、叠合法
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
B
A
C
E
D
F
∠ABC<∠DEF
B
C
A
E
D
F
2、叠合法比较
DE边在∠ABC的外部,则
∠ABC=∠DEF
B
A
C
E
D
F
DE与AB边重合,则
2、叠合法比较
∠ABC>∠DEF
B
A
C
D
E
F
DE边在∠ABC的内部,则
2、叠合法比较
∠ABC=∠DEF
∠ABC<∠DEF
∠ABC>∠DEF
(F)
B
(E)
A
C
(D)
C
B
(E)
A
D
(F)
D
B
(E)
(F)
C
A
2、叠合法比较
说明:
1、两角的顶点必须重合;
2、一边必须重合,另一边落在重合的一边的同侧.
1.角的大小与两边画出部分的长短是否相关?
2.一个30°的角用能放大3倍的放大镜观看,看到的角度有何变化?
仪一仪
A
C
B
O
图中共有几个角?它们之间有什么关系?
二、角的和与差:
图中∠AOC是∠AOB和∠BOC的和,记作:∠AOC=∠AOB+∠BOC
图中∠AOB是∠AOC和∠BOC的差,
记作:∠AOB=∠AOC-∠BOC
那么,图中∠AOC-∠AOB=
∠BOC
认识角的和差
例1 如图,求解下列问题:
(1)试比较∠AOC与∠BOC的大小,∠BOD与∠COD的大小;
(2)将∠AOC写成两个角的和与两个角的差的式.
解:(1)由图可看出:∠AOC>∠BOC,(OB在∠AOC内); ∠BOD>∠COD.(OC在∠B内)
O
A
B
C
D
A
B
C
D
(2)∠AOC=∠AOB+∠BOC;
∠AOC=∠AOD-∠DOC.
O
如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
填一填:
在角的内部,以角的顶点为端点的一条射线把这个角分成两个相等的角,这条射线叫做这个角的平分线(angular bisector)
O
A
B
C
定义:
上图中,∠AOC、∠BOC与∠AOB之间有怎么样的大小关系?它们之间的关系可以怎么表示?
角的平分线:
若OC平分∠AOB,
则∠AOC=∠BOC= ∠AOB ;
或∠AOB=2∠AOC=2∠BOC.
A
B
O
c
几何语言:
例2:如图,∠ABC=90°,∠CBD=30°,BP平分∠ABD. 求∠ABP的度数.
A
B
C
D
P
2. 如图,∠ABC=60°,∠ABD=145°,BE平分∠ABC,求∠DBE的度数
A
B
C
D
E
解: ∵ ∠ABC=60°,∠ABD=145°
∠ABD- ∠ABC
= 145°- 60°=85°
又∵ BE平分∠ABC
∴ ∠CBE= ∠ABC= × 60°= 30°
∠CBD+∠CBE
= 85°+ 30°=115°
∴ ∠CBD=
∴ ∠DBE=
1.如图,∠AOB=50°,OC平分∠AOB,则∠AOC=________°.
25
当堂练习
2.如图,∠1=∠3,那么( ).
A.∠1=∠2 B. ∠2=∠3
C.∠AOC=∠BOD D. ∠1=
C
3.如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD等于( )
A.30° B.35°
C.20° D.40°
B
4.如图,点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.
5.已知射线OA,若从点O引两条射线OB和OC,使∠AOB=50°,∠BOC=20°,求∠AOC的度数.
谈谈这节课的收获……
还有什么困惑……
利用一副三角板,我们能画出哪些度数的角?
探究活动
180
15
135
150
75
105
60
30
45
120
15 ,30 ,45 ,60 ,75 ,90 ,105 ,120 ,135 ,150 ,180 等
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
