微专题 立体几何中有关截面交线的画法 讲义-数学沪教版(2020)必修第三册(Word版含答案)
文档属性
| 名称 | 微专题 立体几何中有关截面交线的画法 讲义-数学沪教版(2020)必修第三册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 793.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 09:45:50 | ||
图片预览



文档简介
学生版
带着如下【问题】思考、理解与应用
两个平面的交线及其画法
利用平面的性质画平面与平面的交线的研究与方法;.
1、作截面首先得依据公理3保障有一个交点,才能保证当且仅当过该的的唯一一条直线;凡是相交的平面都要画出它们的交线.
2、作交线的方法有如下两种:①利用公理3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.;
例1、如图所示,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,
且A l,B l,直线AB与l不平行,
那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
【提示】
【解析】
【说明】本题考查了正确画截面的基础是画交线,而画交线的依据是公理3与公理1;
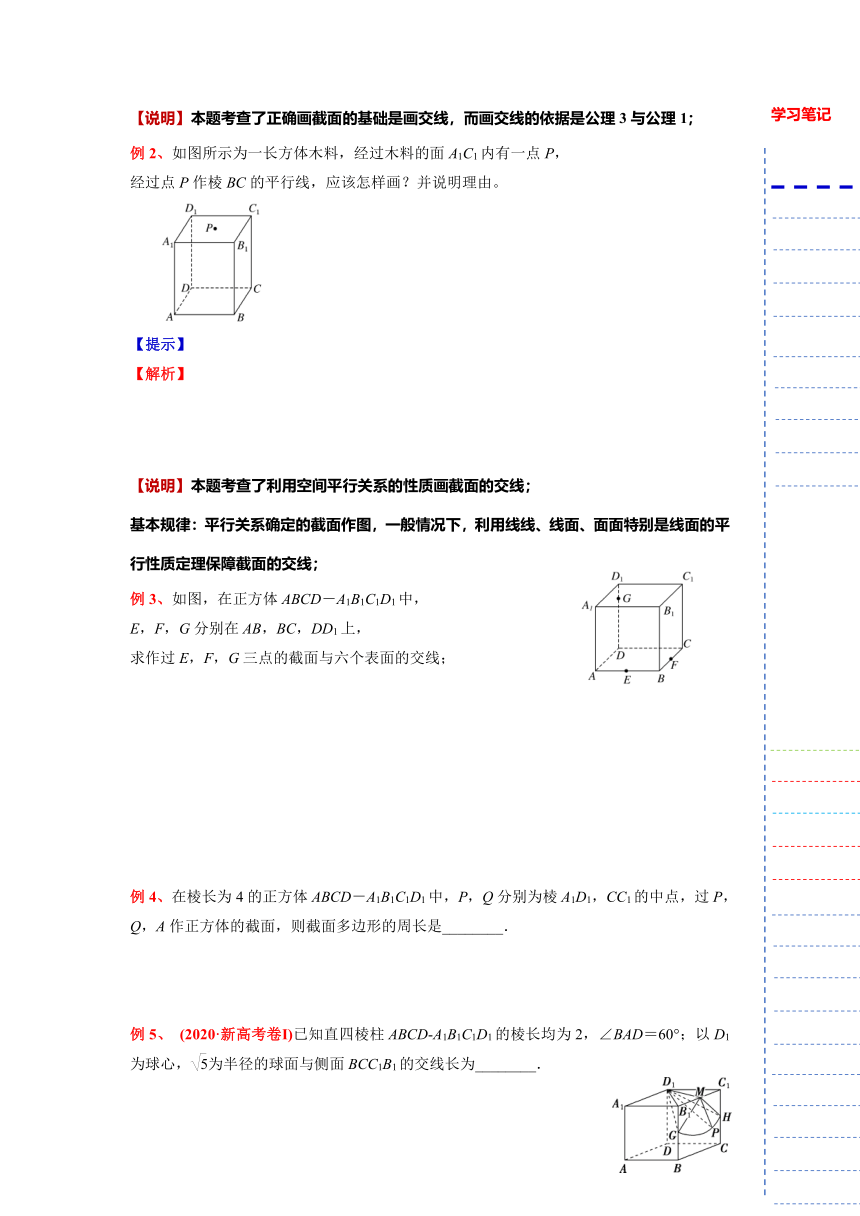
例2、如图所示为一长方体木料,经过木料的面A1C1内有一点P,
经过点P作棱BC的平行线,应该怎样画?并说明理由。
【提示】
【解析】
【说明】本题考查了利用空间平行关系的性质画截面的交线;
基本规律:平行关系确定的截面作图,一般情况下,利用线线、线面、面面特别是线面的平行性质定理保障截面的交线;
例3、如图,在正方体ABCD-A1B1C1D1中,
E,F,G分别在AB,BC,DD1上,
求作过E,F,G三点的截面与六个表面的交线;
例4、在棱长为4的正方体ABCD-A1B1C1D1中,P,Q分别为棱A1D1,CC1的中点,过P,Q,A作正方体的截面,则截面多边形的周长是________.
例5、 (2020·新高考卷Ⅰ)已知直四棱柱ABCD A1B1C1D1的棱长均为2,∠BAD=60°;以D1为球心,为半径的球面与侧面BCC1B1的交线长为________.
作出截面的关键是找到截线,作出截线的主要根据有:
(1)确定平面的条件;
(2)三线共点的条件;
(3)面面平行的性质定理.
1、已知正方体,平面和线段,,,分别交于点E,F,G,H,则截面EFGH的形状不可能是( )
A.梯形 B.正方形 C.长方形 D.菱形
2、如图,在正方体中,E是棱的中点,则过三点A、D1、E的截面过( )
A.AB中点
B.BC中点
C.CD中点
D.BB1中点
3、如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为
4、已知正方体ABCD-A1B1C1D1的棱长为3,E,F分别为BC,CD的中点,P是线段A1B上的动点,C1P与平面D1EF的交点Q的轨迹长为________.
5、在棱长为1的正方体中,,分别为棱,的中点,为棱靠近点的三等分点,用过点,,的平面截正方体,则截面图形的周长为
6、作出平面与四棱锥的截面,截面多边形的边数为______.
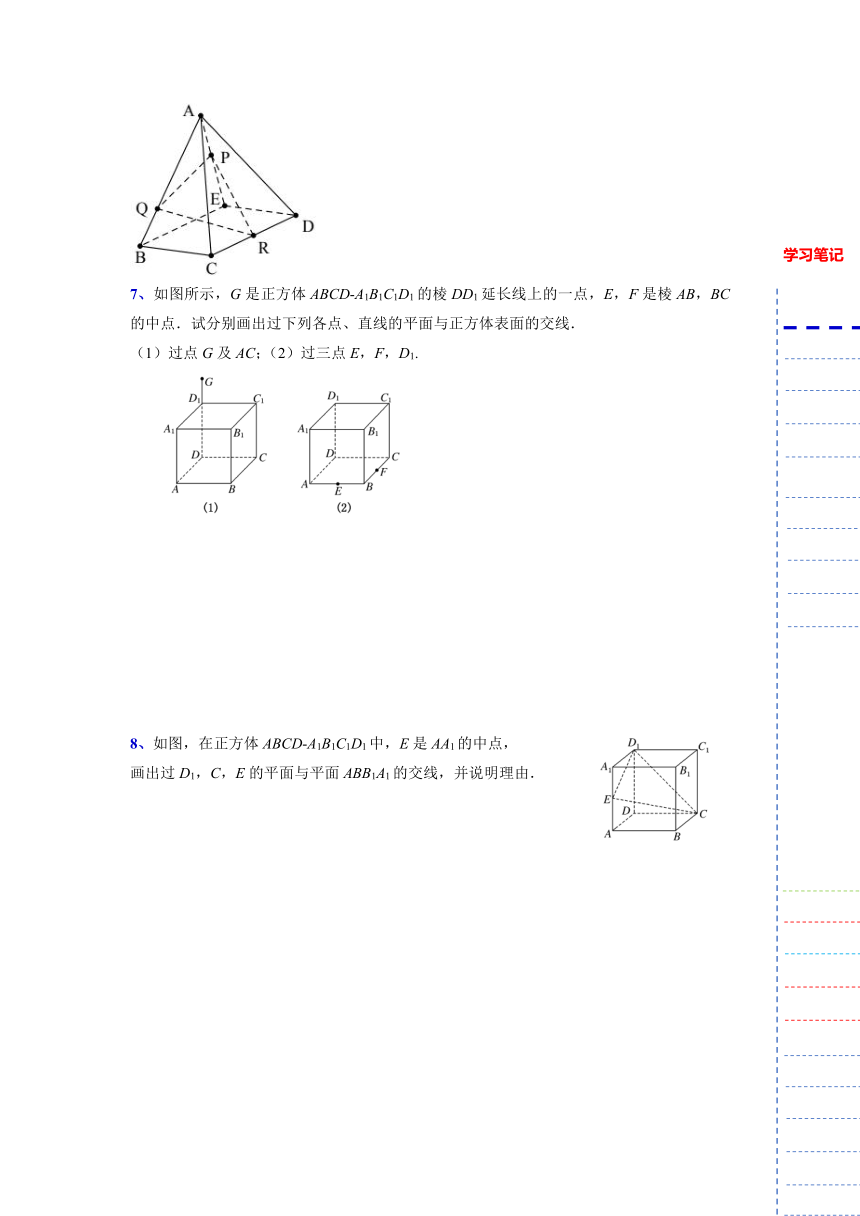
7、如图所示,G是正方体ABCD A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC;(2)过三点E,F,D1.
8、如图,在正方体ABCD A1B1C1D1中,E是AA1的中点,
画出过D1,C,E的平面与平面ABB1A1的交线,并说明理由.
教师版
带着如下【问题】思考、理解与应用
两个平面的交线及其画法
利用平面的性质画平面与平面的交线的研究与方法;.
1、作截面首先得依据公理3保障有一个交点,才能保证当且仅当过该的的唯一一条直线;凡是相交的平面都要画出它们的交线.
2、作交线的方法有如下两种:①利用公理3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.;
例1、如图所示,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,
且A l,B l,直线AB与l不平行,
那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
【提示】注意理解与用好公理3、公理1;
【解析】结论:平面ABC与平面β的交线与l相交;
证明如下:因为AB与l不平行,且AB α,l α,所以AB与l一定相交.
设AB∩l=P,则P∈AB,P∈l;
又因为AB 平面ABC,l β,所以P∈平面ABC,P∈β;
所以,点P是平面ABC与平面β的一个公共点,
而点C也是平面ABC与平面β的一个公共点,
且P,C是不同的两点,
所以直线PC就是平面ABC与平面β的交线;
即平面ABC∩平面β=PC,而PC∩l=P,
所以平面ABC与平面β的交线与l相交;
【说明】本题考查了正确画截面的基础是画交线,而画交线的依据是公理3与公理1;
例2、如图所示为一长方体木料,经过木料的面A1C1内有一点P,
经过点P作棱BC的平行线,应该怎样画?并说明理由。
【提示】“点P作棱BC”不在长方体的侧面与底面上;
【解析】如图所示,在面A1C1内过P作直线EF∥B1C1,
交A1B1于点E,交C1D1于点F,则直线EF即为所求.
理由:因为EF∥B1C1,BC∥B1C1,所以EF∥BC.
【说明】本题考查了利用空间平行关系的性质画截面的交线;
基本规律:平行关系确定的截面作图,一般情况下,利用线线、线面、面面特别是线面的平行性质定理保障截面的交线;
例3、如图,在正方体ABCD-A1B1C1D1中,
E,F,G分别在AB,BC,DD1上,
求作过E,F,G三点的截面与六个表面的交线;
【提示】注意“棱”是表面的交线与平面、直线是无限的;
【作法】
①在底面AC内,过E,F作直线EF,分别与DA,DC的延长线交于L,M.
②在侧面A1D内,连接LG交AA1于K.
③在侧面D1C内,连接GM交CC1于H.
④连接KE,FH.则五边形EFHGK即为所求的截面.
例4、在棱长为4的正方体ABCD-A1B1C1D1中,P,Q分别为棱A1D1,CC1的中点,过P,Q,A作正方体的截面,则截面多边形的周长是________.
【提示】关键是正确作出“交线”,明确截面多边形的形状与交汇性质;
【答案】;
【解析】如图所示,
过Q作QM∥AP交BC于M,
由A1P=CQ=2,tan∠APA1=2,
则tan∠CMQ=2,CM==1,
延长MQ交B1C1的延长线于E点,连接PE,交D1C1于N点,
则多边形AMQNP即为截面,
根据平行线性质有C1E=CM=1,==,则C1N=,D1N=,
因此NQ==,
NP==,
又AP==2,AM==5,
MQ==,
所以多边形AMQNP的周长为
AM+MQ+QN+NP+PA=5++++2=.
【说明】本题主要考查了正确画截面的交线及其应用;
例5、 (2020·新高考卷Ⅰ)已知直四棱柱ABCD A1B1C1D1的棱长均为2,∠BAD=60°;以D1为球心,为半径的球面与侧面BCC1B1的交线长为________.
【答案】(供高三复习用)
【解析】如图,连接B1D1,易知△B1C1D1为正三角形,
所以B1D1=C1D1=2.分别取B1C1,BB1,CC1的中点M,G,H,
连接D1M,D1G,D1H,则易得D1G=D1H==,
D1M⊥B1C1,且D1M=;
由题意知G,H分别是BB1,CC1与球面的交点.
在侧面BCC1B1内任取一点P,使MP=,连接D1P,
则D1P= ==,
连接MG,MH,易得MG=MH=,
故可知以M为圆心,为半径的圆弧GH为球面与侧面BCC1B1的交线.
由∠B1MG=∠C1MH=45°知∠GMH=90°,所以的长为×2π×=.
【说明】解答此类题;(1)挖掘题目条件,要抓住截面的点是公共点这个关键;(2)灵活转化,将条件转化到一个平面内,寻找截面上的点满足的数量关系;
作出截面的关键是找到截线,作出截线的主要根据有:
(1)确定平面的条件;
(2)三线共点的条件;
(3)面面平行的性质定理.
1、已知正方体,平面和线段,,,分别交于点E,F,G,H,则截面EFGH的形状不可能是( )
A.梯形 B.正方形 C.长方形 D.菱形
【提示】根据面面平行的性质定理,可以得出,,由此可推断四边形EFGH一定为平行四边形,从而可得出答案.
【答案】A
【解析】因为面面,面面,面面,所以,
同理可得,所以四边形EFGH为平行四边形,所以截面EFGH的形状不可能是梯形.
若面面,此时四边形EFGH是正方形,也是菱形;
当是所在棱的中点,分别与 重合时,四边形EFGH是长方形.
故选:A.
2、如图,在正方体中,E是棱的中点,则过三点A、D1、E的截面过( )
A.AB中点
B.BC中点
C.CD中点
D.BB1中点
【提示】根据截面特点结合正方形结构性质求解.
【答案】B
【详解】取的中点,连接,,
如图,则,
所以在截面上,故选:B
3、如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为
【答案】等腰梯形
【解析】取BC的中点H,连接AH,GH,AD1,D1G,
由题意得GH∥EF,AH∥A1F,
又GH 平面A1EF,EF 平面A1EF,
∴GH∥平面A1EF,同理AH∥平面A1EF,
又GH∩AH=H,GH,AH 平面AHGD1,
∴平面AHGD1∥平面A1EF,
故过线段AG且与平面A1EF平行的截面图形为四边形AHGD1,显然为等腰梯形.
4、已知正方体ABCD-A1B1C1D1的棱长为3,E,F分别为BC,CD的中点,P是线段A1B上的动点,C1P与平面D1EF的交点Q的轨迹长为________.
【答案】
【解析】如图所示,
连接EF,A1B,连接A1C1,B1D1交于点M,连接B1E,BC1交于点N,
由EF∥B1D1,即E,F,B1,D1共面,
由P是线段A1B上的动点,当P重合于A1或B时,C1A1,C1B与平面D1EF的交点分别为M,N,
即Q的轨迹为MN,
由棱长为3,
得C1M=A1C1=3,则BC1=6,
又==,
则NC1=BC1=4,
由A1B=BC1=A1C1,
得∠A1C1B=60°,
则MN=
==.
5、在棱长为1的正方体中,,分别为棱,的中点,为棱靠近点的三等分点,用过点,,的平面截正方体,则截面图形的周长为
【答案】
【解析】根据题意作出截面如图,
利用勾股定理和对边相等易得周长为,故选:.
6、作出平面与四棱锥的截面,截面多边形的边数为______.
【答案】五
【解析】延长的延长线于,连接的延长线于
连接于,连接,则五边形即为所求.
所以截面多边形的边数为五.
7、如图所示,G是正方体ABCD A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC;(2)过三点E,F,D1.
【解析】(1)画法:连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.
(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.
8、如图,在正方体ABCD A1B1C1D1中,E是AA1的中点,
画出过D1,C,E的平面与平面ABB1A1的交线,并说明理由.
【解析】如图,取AB的中点F,连接EF,A1B,CF.
∵E是AA1的中点,
∴EF∥A1B.
在正方体ABCD A1B1C1D1中,A1D1∥BC,A1D1=BC,
∴四边形A1BCD1是平行四边形.
∴A1B∥CD1,
∴EF∥CD1.
∴E,F,C,D1四点共面.
∵E∈平面ABB1A1,E∈平面D1CE,
F∈平面ABB1A1,F∈平面D1CE,
∴平面ABB1A1∩平面D1CE=EF.
∴过D1,C,E的平面与平面ABB1A1的交线为EF.
带着如下【问题】思考、理解与应用
两个平面的交线及其画法
利用平面的性质画平面与平面的交线的研究与方法;.
1、作截面首先得依据公理3保障有一个交点,才能保证当且仅当过该的的唯一一条直线;凡是相交的平面都要画出它们的交线.
2、作交线的方法有如下两种:①利用公理3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.;
例1、如图所示,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,
且A l,B l,直线AB与l不平行,
那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
【提示】
【解析】
【说明】本题考查了正确画截面的基础是画交线,而画交线的依据是公理3与公理1;
例2、如图所示为一长方体木料,经过木料的面A1C1内有一点P,
经过点P作棱BC的平行线,应该怎样画?并说明理由。
【提示】
【解析】
【说明】本题考查了利用空间平行关系的性质画截面的交线;
基本规律:平行关系确定的截面作图,一般情况下,利用线线、线面、面面特别是线面的平行性质定理保障截面的交线;
例3、如图,在正方体ABCD-A1B1C1D1中,
E,F,G分别在AB,BC,DD1上,
求作过E,F,G三点的截面与六个表面的交线;
例4、在棱长为4的正方体ABCD-A1B1C1D1中,P,Q分别为棱A1D1,CC1的中点,过P,Q,A作正方体的截面,则截面多边形的周长是________.
例5、 (2020·新高考卷Ⅰ)已知直四棱柱ABCD A1B1C1D1的棱长均为2,∠BAD=60°;以D1为球心,为半径的球面与侧面BCC1B1的交线长为________.
作出截面的关键是找到截线,作出截线的主要根据有:
(1)确定平面的条件;
(2)三线共点的条件;
(3)面面平行的性质定理.
1、已知正方体,平面和线段,,,分别交于点E,F,G,H,则截面EFGH的形状不可能是( )
A.梯形 B.正方形 C.长方形 D.菱形
2、如图,在正方体中,E是棱的中点,则过三点A、D1、E的截面过( )
A.AB中点
B.BC中点
C.CD中点
D.BB1中点
3、如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为
4、已知正方体ABCD-A1B1C1D1的棱长为3,E,F分别为BC,CD的中点,P是线段A1B上的动点,C1P与平面D1EF的交点Q的轨迹长为________.
5、在棱长为1的正方体中,,分别为棱,的中点,为棱靠近点的三等分点,用过点,,的平面截正方体,则截面图形的周长为
6、作出平面与四棱锥的截面,截面多边形的边数为______.
7、如图所示,G是正方体ABCD A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC;(2)过三点E,F,D1.
8、如图,在正方体ABCD A1B1C1D1中,E是AA1的中点,
画出过D1,C,E的平面与平面ABB1A1的交线,并说明理由.
教师版
带着如下【问题】思考、理解与应用
两个平面的交线及其画法
利用平面的性质画平面与平面的交线的研究与方法;.
1、作截面首先得依据公理3保障有一个交点,才能保证当且仅当过该的的唯一一条直线;凡是相交的平面都要画出它们的交线.
2、作交线的方法有如下两种:①利用公理3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.;
例1、如图所示,已知平面α∩β=l,点A∈α,点B∈α,点C∈β,
且A l,B l,直线AB与l不平行,
那么平面ABC与平面β的交线与l有什么关系?证明你的结论.
【提示】注意理解与用好公理3、公理1;
【解析】结论:平面ABC与平面β的交线与l相交;
证明如下:因为AB与l不平行,且AB α,l α,所以AB与l一定相交.
设AB∩l=P,则P∈AB,P∈l;
又因为AB 平面ABC,l β,所以P∈平面ABC,P∈β;
所以,点P是平面ABC与平面β的一个公共点,
而点C也是平面ABC与平面β的一个公共点,
且P,C是不同的两点,
所以直线PC就是平面ABC与平面β的交线;
即平面ABC∩平面β=PC,而PC∩l=P,
所以平面ABC与平面β的交线与l相交;
【说明】本题考查了正确画截面的基础是画交线,而画交线的依据是公理3与公理1;
例2、如图所示为一长方体木料,经过木料的面A1C1内有一点P,
经过点P作棱BC的平行线,应该怎样画?并说明理由。
【提示】“点P作棱BC”不在长方体的侧面与底面上;
【解析】如图所示,在面A1C1内过P作直线EF∥B1C1,
交A1B1于点E,交C1D1于点F,则直线EF即为所求.
理由:因为EF∥B1C1,BC∥B1C1,所以EF∥BC.
【说明】本题考查了利用空间平行关系的性质画截面的交线;
基本规律:平行关系确定的截面作图,一般情况下,利用线线、线面、面面特别是线面的平行性质定理保障截面的交线;
例3、如图,在正方体ABCD-A1B1C1D1中,
E,F,G分别在AB,BC,DD1上,
求作过E,F,G三点的截面与六个表面的交线;
【提示】注意“棱”是表面的交线与平面、直线是无限的;
【作法】
①在底面AC内,过E,F作直线EF,分别与DA,DC的延长线交于L,M.
②在侧面A1D内,连接LG交AA1于K.
③在侧面D1C内,连接GM交CC1于H.
④连接KE,FH.则五边形EFHGK即为所求的截面.
例4、在棱长为4的正方体ABCD-A1B1C1D1中,P,Q分别为棱A1D1,CC1的中点,过P,Q,A作正方体的截面,则截面多边形的周长是________.
【提示】关键是正确作出“交线”,明确截面多边形的形状与交汇性质;
【答案】;
【解析】如图所示,
过Q作QM∥AP交BC于M,
由A1P=CQ=2,tan∠APA1=2,
则tan∠CMQ=2,CM==1,
延长MQ交B1C1的延长线于E点,连接PE,交D1C1于N点,
则多边形AMQNP即为截面,
根据平行线性质有C1E=CM=1,==,则C1N=,D1N=,
因此NQ==,
NP==,
又AP==2,AM==5,
MQ==,
所以多边形AMQNP的周长为
AM+MQ+QN+NP+PA=5++++2=.
【说明】本题主要考查了正确画截面的交线及其应用;
例5、 (2020·新高考卷Ⅰ)已知直四棱柱ABCD A1B1C1D1的棱长均为2,∠BAD=60°;以D1为球心,为半径的球面与侧面BCC1B1的交线长为________.
【答案】(供高三复习用)
【解析】如图,连接B1D1,易知△B1C1D1为正三角形,
所以B1D1=C1D1=2.分别取B1C1,BB1,CC1的中点M,G,H,
连接D1M,D1G,D1H,则易得D1G=D1H==,
D1M⊥B1C1,且D1M=;
由题意知G,H分别是BB1,CC1与球面的交点.
在侧面BCC1B1内任取一点P,使MP=,连接D1P,
则D1P= ==,
连接MG,MH,易得MG=MH=,
故可知以M为圆心,为半径的圆弧GH为球面与侧面BCC1B1的交线.
由∠B1MG=∠C1MH=45°知∠GMH=90°,所以的长为×2π×=.
【说明】解答此类题;(1)挖掘题目条件,要抓住截面的点是公共点这个关键;(2)灵活转化,将条件转化到一个平面内,寻找截面上的点满足的数量关系;
作出截面的关键是找到截线,作出截线的主要根据有:
(1)确定平面的条件;
(2)三线共点的条件;
(3)面面平行的性质定理.
1、已知正方体,平面和线段,,,分别交于点E,F,G,H,则截面EFGH的形状不可能是( )
A.梯形 B.正方形 C.长方形 D.菱形
【提示】根据面面平行的性质定理,可以得出,,由此可推断四边形EFGH一定为平行四边形,从而可得出答案.
【答案】A
【解析】因为面面,面面,面面,所以,
同理可得,所以四边形EFGH为平行四边形,所以截面EFGH的形状不可能是梯形.
若面面,此时四边形EFGH是正方形,也是菱形;
当是所在棱的中点,分别与 重合时,四边形EFGH是长方形.
故选:A.
2、如图,在正方体中,E是棱的中点,则过三点A、D1、E的截面过( )
A.AB中点
B.BC中点
C.CD中点
D.BB1中点
【提示】根据截面特点结合正方形结构性质求解.
【答案】B
【详解】取的中点,连接,,
如图,则,
所以在截面上,故选:B
3、如图,在正方体ABCD-A1B1C1D1中,点E,F分别是棱B1B,B1C1的中点,点G是棱C1C的中点,则过线段AG且平行于平面A1EF的截面图形为
【答案】等腰梯形
【解析】取BC的中点H,连接AH,GH,AD1,D1G,
由题意得GH∥EF,AH∥A1F,
又GH 平面A1EF,EF 平面A1EF,
∴GH∥平面A1EF,同理AH∥平面A1EF,
又GH∩AH=H,GH,AH 平面AHGD1,
∴平面AHGD1∥平面A1EF,
故过线段AG且与平面A1EF平行的截面图形为四边形AHGD1,显然为等腰梯形.
4、已知正方体ABCD-A1B1C1D1的棱长为3,E,F分别为BC,CD的中点,P是线段A1B上的动点,C1P与平面D1EF的交点Q的轨迹长为________.
【答案】
【解析】如图所示,
连接EF,A1B,连接A1C1,B1D1交于点M,连接B1E,BC1交于点N,
由EF∥B1D1,即E,F,B1,D1共面,
由P是线段A1B上的动点,当P重合于A1或B时,C1A1,C1B与平面D1EF的交点分别为M,N,
即Q的轨迹为MN,
由棱长为3,
得C1M=A1C1=3,则BC1=6,
又==,
则NC1=BC1=4,
由A1B=BC1=A1C1,
得∠A1C1B=60°,
则MN=
==.
5、在棱长为1的正方体中,,分别为棱,的中点,为棱靠近点的三等分点,用过点,,的平面截正方体,则截面图形的周长为
【答案】
【解析】根据题意作出截面如图,
利用勾股定理和对边相等易得周长为,故选:.
6、作出平面与四棱锥的截面,截面多边形的边数为______.
【答案】五
【解析】延长的延长线于,连接的延长线于
连接于,连接,则五边形即为所求.
所以截面多边形的边数为五.
7、如图所示,G是正方体ABCD A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC;(2)过三点E,F,D1.
【解析】(1)画法:连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.
(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.
8、如图,在正方体ABCD A1B1C1D1中,E是AA1的中点,
画出过D1,C,E的平面与平面ABB1A1的交线,并说明理由.
【解析】如图,取AB的中点F,连接EF,A1B,CF.
∵E是AA1的中点,
∴EF∥A1B.
在正方体ABCD A1B1C1D1中,A1D1∥BC,A1D1=BC,
∴四边形A1BCD1是平行四边形.
∴A1B∥CD1,
∴EF∥CD1.
∴E,F,C,D1四点共面.
∵E∈平面ABB1A1,E∈平面D1CE,
F∈平面ABB1A1,F∈平面D1CE,
∴平面ABB1A1∩平面D1CE=EF.
∴过D1,C,E的平面与平面ABB1A1的交线为EF.
同课章节目录
