微专题 空间两直线位置关系及其判别与求解 讲义-数学沪教版(2020)必修第三册(Word版含答案)
文档属性
| 名称 | 微专题 空间两直线位置关系及其判别与求解 讲义-数学沪教版(2020)必修第三册(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 646.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-30 00:00:00 | ||
图片预览





文档简介
学生版
带着如下【问题】思考、理解与应用
1、空间两直线有哪几种位置关系?
2、什么是异面直线?
3、什么是异面直线所成的角?
1、异面直线
(1)定义:不同在任何一个平面内的两条直线.
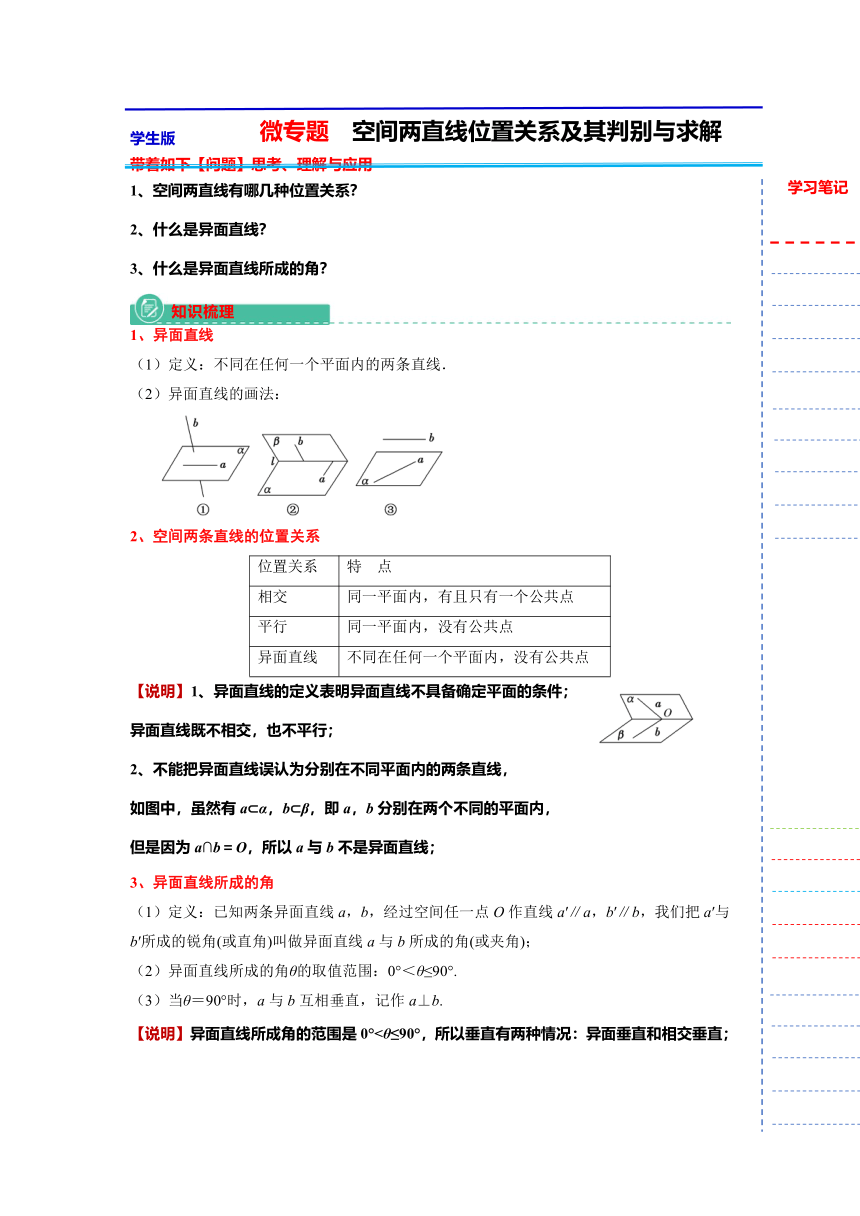
(2)异面直线的画法:
2、空间两条直线的位置关系
位置关系 特 点
相交 同一平面内,有且只有一个公共点
平行 同一平面内,没有公共点
异面直线 不同在任何一个平面内,没有公共点
【说明】1、异面直线的定义表明异面直线不具备确定平面的条件;
异面直线既不相交,也不平行;
2、不能把异面直线误认为分别在不同平面内的两条直线,
如图中,虽然有a α,b β,即a,b分别在两个不同的平面内,
但是因为a∩b=O,所以a与b不是异面直线;
3、异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角);
(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)当θ=90°时,a与b互相垂直,记作a⊥b.
【说明】异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:异面垂直和相交垂直;
例1、如图,在长方体ABCD A1B1C1D1中,
(1)直线A1B与直线D1C的位置关系是________;
(2)直线A1B与直线B1C的位置关系是________;
(3)直线D1D与直线D1C的位置关系是________;
(4)直线AB与直线B1C的位置关系是________.
【提示】
【答案】
【解析】
【说明】本题考查了两直线位置关系的判定;
1、判定两条直线平行或相交的方法:判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断;
2、判定两条直线是异面直线的方法:
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图);
例2、如图所示,已知两个正方形和不在同一平面内,
为的中点;
证明:直线与是异面直线;
【提示】
【证明】方法1、
方法2、
【说明】判定空间两条直线是异面直线的方法:
1、定义法:不同在任何一个平面内的两条直线;
2、判定定理:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线;
3、反证法:证明两线不可能平行、相交或证明两线不可能共面,从而可得两线异面;
例3、在正方体ABCD A1B1C1D1中,E,F分别是A1B1,B1C1的中点,
求异面直线DB1与EF所成角的大小;
【提示】常规方法主要在根据题设“找角”;
【解析】方法1、
方法2、
方法3、
方法4、
【说明】本题考查了异面直线所成角及其求法;
求两异面直线所成的角的三个步骤
(1)作:根据所成角的定义,用平移法作出异面直线所成的角;
(2)证:证明作出的角就是要求的角;
(3)算:求角的值,常利用解三角形得出;
(4)答:根据题设要求回答;
可用“一作二证三算四答”来概括.同时注意异面直线所成角范围是0°<θ≤90°;
1、对于异面直线的定义的理解
异面直线是不同在任何一个平面内的两条直线.
注意异面直线定义中“任何”两字,它指空间中的所有平面,
因此异面直线也可以理解为:在空间中找不到一个平面,
使其同时经过a,b两条直线.例如,如图所示的长方体中,棱AB和B1C1所在的直线既不平行又不相交,找不到一个平面同时经过这两条棱所在的直线,故AB与B1C1是异面直线.
2、空间两条直线的位置关系
(1)若从有无公共点的角度来看,可分为两类:
直线
(2)若从是否共面的角度看,也可分两类:
直线
3、判定两条直线平行或相交的方法
判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
4、判定两条直线是异面直线的方法
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,
和这个平面内不经过此点的直线是异面直线;
用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
(3)反证法;
1、如果两条直线a和b没有公共点,那么a与b的位置关系是( )
A.共面 B.平行 C.异面 D.平行或异面
2、在空间四边形ABCD中,E,F分别为对角线AC,BD的中点,则BE与CF( )
A.平行 B.异面 C.相交 D.以上均有可能
3、若a,b为异面直线,直线c∥a,则c与b的位置关系是
4、已知直线a,b,c,下列三个命题:
①若a与b异面,b与c异面,则a与c异面;
②若a∥b,a和c相交,则b和c也相交;
③若a⊥b,a⊥c,则b∥c;
其中,正确命题的个数是
5、如图所示,正方体ABCD A1B1C1D1中,
E,F分别是棱BC,CC1的中点,
则异面直线EF与B1D1所成的角为__________.
6、如图,空间四边形ABCD的对角线AC=8,BD=6,
M,N分别为AB,CD的中点,
并且异面直线AC与BD所成的角为90°,
则MN等于________.
7、已知A、B、C、D是空间四个点,且直线AB与CD是两条异面直线;
用反证法证明:直线AC与BD也是异面直线.
8、如图所示,点A是△BCD所在平面外一点,AD=BC,
E,F分别是AB,CD的中点,当EF=AD时,
求:异面直线AD和BC所成的角.
教师版
带着如下【问题】思考、理解与应用
1、空间两直线有哪几种位置关系?
2、什么是异面直线?
3、什么是异面直线所成的角?
1、异面直线
(1)定义:不同在任何一个平面内的两条直线.
(2)异面直线的画法:
2、空间两条直线的位置关系
位置关系 特 点
相交 同一平面内,有且只有一个公共点
平行 同一平面内,没有公共点
异面直线 不同在任何一个平面内,没有公共点
【说明】1、异面直线的定义表明异面直线不具备确定平面的条件;
异面直线既不相交,也不平行;
2、不能把异面直线误认为分别在不同平面内的两条直线,
如图中,虽然有a α,b β,即a,b分别在两个不同的平面内,
但是因为a∩b=O,所以a与b不是异面直线;
3、异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角);
(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)当θ=90°时,a与b互相垂直,记作a⊥b.
【说明】异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:异面垂直和相交垂直;
例1、如图,在长方体ABCD A1B1C1D1中,
(1)直线A1B与直线D1C的位置关系是________;
(2)直线A1B与直线B1C的位置关系是________;
(3)直线D1D与直线D1C的位置关系是________;
(4)直线AB与直线B1C的位置关系是________.
【提示】注意:理解空间两直线的位置关系及其判断标准;
【答案】(1)平行;(2)异面;(3)相交;(4)异面;
【解析】(1)在长方体ABCD A1B1C1D1中,A1D1∥BC且A1D1=BC,
所以,四边形A1BCD1为平行四边形,所以,A1B∥D1C;
(2)直线A1B与直线B1C不同在任何一个平面内;
(3)直线D1D与直线D1C相交于点D1;
(4)直线AB与直线B1C不同在任何一个平面内;
【说明】本题考查了两直线位置关系的判定;
1、判定两条直线平行或相交的方法:判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断;
2、判定两条直线是异面直线的方法:
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图);
例2、如图所示,已知两个正方形和不在同一平面内,
为的中点;
证明:直线与是异面直线;
【提示】注意:从集合视角理解“已知两个正方形和不在同一平面内”;
假设共面,由此推得∥平面,再求线面平行的性质推得线线平行,
即可退出矛盾;或紧扣判定定理的条件;
【证明】方法1、假设直线与共面,
则平面与平面交于,
又由已知可得////,且,
所以,四边形为平行四边形,则,
又直线不在平面内,直线平面,所以,∥平面,
所以,,所以,∥,这与矛盾,故假设不成立,
所以,与不共面,它们是异面直线;
方法2、因为,点为的中点;
所以,点不在平面,点不在直线上,
所以,由判定定理得直线与是异面直线;
【说明】判定空间两条直线是异面直线的方法:
1、定义法:不同在任何一个平面内的两条直线;
2、判定定理:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线;
3、反证法:证明两线不可能平行、相交或证明两线不可能共面,从而可得两线异面;
例3、在正方体ABCD A1B1C1D1中,E,F分别是A1B1,B1C1的中点,
求异面直线DB1与EF所成角的大小;
【提示】常规方法主要在根据题设“找角”;
【解析】方法1、如图1所示,连接A1C1,B1D1,
并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G,
则OG∥B1D,EF∥A1C1,
∴∠GOA1为异面直线DB1与EF所成的角(或其补角).
∵GA1=GC1,O为A1C1的中点, 图1
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
方法2、 如图2所示,连接A1D,取A1D的中点H,连接HE,
则HE綊DB1,于是∠HEF为异面直线DB1与EF所成的角(或其补角).
连接HF,设AA1=1,
则EF=,HE=,
取A1D1的中点I,连接HI,IF, 图2
则HI⊥IF,∴HF2=HI2+IF2=,
∴HF2=EF2+HE2,∴∠HEF=90°.
∴异面直线DB1与EF所成的角为90°;
方法3、如图3,连接A1C1,分别取AA1,CC1的中点M,N,连接MN.
∵E,F分别是A1B1,B1C1的中点,
∴EF∥A1C1,又MN∥A1C1,∴MN∥EF.
连接DM,B1N,MB1,DN,则B1N綊DM,
∴四边形DMB1N为平行四边形,
∴MN与DB1必相交,设交点为P,
则∠DPM为异面直线DB1与EF所成的角(或其补角).
设AA1=k(k>0),则MP=k,DM=k,DP=k, 图3
∴DM2=DP2+MP2,∴∠DPM=90°.
∴异面直线DB1与EF所成的角为90°.
方法4、如图4,在原正方体的右侧补上一个全等的正方体,连接B1Q,易得B1Q∥EF,
∴∠DB1Q就是异面直线DB1与EF所成的角(或其补角).
设AA1=k(k>0),
则B1D=k,DQ=k,B1Q=k,
∴B1D2+B1Q2=DQ2,∴∠DB1Q=90°.
∴异面直线DB1与EF所成的角为90°.
【说明】本题考查了异面直线所成角及其求法;
求两异面直线所成的角的三个步骤
(1)作:根据所成角的定义,用平移法作出异面直线所成的角;
(2)证:证明作出的角就是要求的角;
(3)算:求角的值,常利用解三角形得出;
(4)答:根据题设要求回答;
可用“一作二证三算四答”来概括.同时注意异面直线所成角范围是0°<θ≤90°;
1、对于异面直线的定义的理解
异面直线是不同在任何一个平面内的两条直线.
注意异面直线定义中“任何”两字,它指空间中的所有平面,
因此异面直线也可以理解为:在空间中找不到一个平面,
使其同时经过a,b两条直线.例如,如图所示的长方体中,棱AB和B1C1所在的直线既不平行又不相交,找不到一个平面同时经过这两条棱所在的直线,故AB与B1C1是异面直线.
2、空间两条直线的位置关系
(1)若从有无公共点的角度来看,可分为两类:
直线
(2)若从是否共面的角度看,也可分两类:
直线
3、判定两条直线平行或相交的方法
判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
4、判定两条直线是异面直线的方法
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,
和这个平面内不经过此点的直线是异面直线;
用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
(3)反证法;
1、如果两条直线a和b没有公共点,那么a与b的位置关系是( )
A.共面 B.平行 C.异面 D.平行或异面
【答案】D;
【解析】空间中两直线的位置关系有:①相交;②平行;③异面.两条直线平行和两条直线异面都满足两条直线没有公共点,故a与b的位置关系是平行或异面.
2、在空间四边形ABCD中,E,F分别为对角线AC,BD的中点,则BE与CF( )
A.平行 B.异面 C.相交 D.以上均有可能
【答案】B;
【解析】假设BE与CF是共面直线,设此平面为α,则E,F,B,C∈α,所以BF,CE α,而A∈CE,D∈BF,所以A,D∈α,即有A,B,C,D∈α,与ABCD为空间四边形矛盾,所以BE与CF是异面直线,故选B.
3、若a,b为异面直线,直线c∥a,则c与b的位置关系是
【答案】异面或相交
【解析】由空间直线的位置关系,知c与b可能异面或相交
4、已知直线a,b,c,下列三个命题:
①若a与b异面,b与c异面,则a与c异面;
②若a∥b,a和c相交,则b和c也相交;
③若a⊥b,a⊥c,则b∥c;
其中,正确命题的个数是
【答案】0;
【解析】①不正确如图;
②不正确,有可能相交也有可能异面;
③不正确.可能平行,可能相交也可能异面.
5、如图所示,正方体ABCD A1B1C1D1中,
E,F分别是棱BC,CC1的中点,
则异面直线EF与B1D1所成的角为__________.
【答案】60°;
【解析】连接BC1,AD1,AB1,
则EF为△BCC1的中位线,
∴EF∥BC1.又∵AB綊CD綊C1D1,
∴四边形ABC1D1为平行四边形.
∴BC1∥AD1.∴EF∥AD1.
∴∠AD1B1为异面直线EF和B1D1所成的角或其补角.
在△AB1D1中,易知AB1=B1D1=AD1,
∴△AB1D1为正三角形,∴∠AD1B1=60°.
∴EF与B1D1所成的角为60°.
6、如图,空间四边形ABCD的对角线AC=8,BD=6,
M,N分别为AB,CD的中点,
并且异面直线AC与BD所成的角为90°,
则MN等于________.
【答案】答案:60°;;
【解析】取AD的中点P,连接PM,PN,
则BD∥PM,AC∥PN,
∴∠MPN即异面直线AC与BD
所成的角,∴∠MPN=90°,
PN=AC=4,PM=BD=3,
∴MN=5.
7、已知A、B、C、D是空间四个点,且直线AB与CD是两条异面直线;
用反证法证明:直线AC与BD也是异面直线.
【提示】根据用反证法证明数学命题的方法和步骤,先假设直线AC、BD是共面直线,再推出错误结论,即可得证;
【解析】假设直线AC、BD是共面直线;
则A,B,C,D四点共面,
所以AB、CD共面,这与AB、CD是异面直线矛盾;
所以假设错误,即直线AC、BD也是异面直线.
8、如图所示,点A是△BCD所在平面外一点,AD=BC,
E,F分别是AB,CD的中点,当EF=AD时,
求:异面直线AD和BC所成的角.
【解析】如图所示,设G为AC的中点,连接EG,FG.
∵E,F,G分别为AB,CD,AC的中点.
∴EG∥BC,且EG=BC;
FG∥AD,且FG=AD.
又AD=BC,∴EG=FG=AD,
∴EG与GF所成的锐角(或直角)即为AD与BC所成的角.
在△EFG中,∵EG=FG=AD,又EF=AD,
∴EG2+FG2=EF2,即EG⊥FG.
∴∠EGF=90°.故AD与BC所成角为90°;
带着如下【问题】思考、理解与应用
1、空间两直线有哪几种位置关系?
2、什么是异面直线?
3、什么是异面直线所成的角?
1、异面直线
(1)定义:不同在任何一个平面内的两条直线.
(2)异面直线的画法:
2、空间两条直线的位置关系
位置关系 特 点
相交 同一平面内,有且只有一个公共点
平行 同一平面内,没有公共点
异面直线 不同在任何一个平面内,没有公共点
【说明】1、异面直线的定义表明异面直线不具备确定平面的条件;
异面直线既不相交,也不平行;
2、不能把异面直线误认为分别在不同平面内的两条直线,
如图中,虽然有a α,b β,即a,b分别在两个不同的平面内,
但是因为a∩b=O,所以a与b不是异面直线;
3、异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角);
(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)当θ=90°时,a与b互相垂直,记作a⊥b.
【说明】异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:异面垂直和相交垂直;
例1、如图,在长方体ABCD A1B1C1D1中,
(1)直线A1B与直线D1C的位置关系是________;
(2)直线A1B与直线B1C的位置关系是________;
(3)直线D1D与直线D1C的位置关系是________;
(4)直线AB与直线B1C的位置关系是________.
【提示】
【答案】
【解析】
【说明】本题考查了两直线位置关系的判定;
1、判定两条直线平行或相交的方法:判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断;
2、判定两条直线是异面直线的方法:
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图);
例2、如图所示,已知两个正方形和不在同一平面内,
为的中点;
证明:直线与是异面直线;
【提示】
【证明】方法1、
方法2、
【说明】判定空间两条直线是异面直线的方法:
1、定义法:不同在任何一个平面内的两条直线;
2、判定定理:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线;
3、反证法:证明两线不可能平行、相交或证明两线不可能共面,从而可得两线异面;
例3、在正方体ABCD A1B1C1D1中,E,F分别是A1B1,B1C1的中点,
求异面直线DB1与EF所成角的大小;
【提示】常规方法主要在根据题设“找角”;
【解析】方法1、
方法2、
方法3、
方法4、
【说明】本题考查了异面直线所成角及其求法;
求两异面直线所成的角的三个步骤
(1)作:根据所成角的定义,用平移法作出异面直线所成的角;
(2)证:证明作出的角就是要求的角;
(3)算:求角的值,常利用解三角形得出;
(4)答:根据题设要求回答;
可用“一作二证三算四答”来概括.同时注意异面直线所成角范围是0°<θ≤90°;
1、对于异面直线的定义的理解
异面直线是不同在任何一个平面内的两条直线.
注意异面直线定义中“任何”两字,它指空间中的所有平面,
因此异面直线也可以理解为:在空间中找不到一个平面,
使其同时经过a,b两条直线.例如,如图所示的长方体中,棱AB和B1C1所在的直线既不平行又不相交,找不到一个平面同时经过这两条棱所在的直线,故AB与B1C1是异面直线.
2、空间两条直线的位置关系
(1)若从有无公共点的角度来看,可分为两类:
直线
(2)若从是否共面的角度看,也可分两类:
直线
3、判定两条直线平行或相交的方法
判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
4、判定两条直线是异面直线的方法
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,
和这个平面内不经过此点的直线是异面直线;
用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
(3)反证法;
1、如果两条直线a和b没有公共点,那么a与b的位置关系是( )
A.共面 B.平行 C.异面 D.平行或异面
2、在空间四边形ABCD中,E,F分别为对角线AC,BD的中点,则BE与CF( )
A.平行 B.异面 C.相交 D.以上均有可能
3、若a,b为异面直线,直线c∥a,则c与b的位置关系是
4、已知直线a,b,c,下列三个命题:
①若a与b异面,b与c异面,则a与c异面;
②若a∥b,a和c相交,则b和c也相交;
③若a⊥b,a⊥c,则b∥c;
其中,正确命题的个数是
5、如图所示,正方体ABCD A1B1C1D1中,
E,F分别是棱BC,CC1的中点,
则异面直线EF与B1D1所成的角为__________.
6、如图,空间四边形ABCD的对角线AC=8,BD=6,
M,N分别为AB,CD的中点,
并且异面直线AC与BD所成的角为90°,
则MN等于________.
7、已知A、B、C、D是空间四个点,且直线AB与CD是两条异面直线;
用反证法证明:直线AC与BD也是异面直线.
8、如图所示,点A是△BCD所在平面外一点,AD=BC,
E,F分别是AB,CD的中点,当EF=AD时,
求:异面直线AD和BC所成的角.
教师版
带着如下【问题】思考、理解与应用
1、空间两直线有哪几种位置关系?
2、什么是异面直线?
3、什么是异面直线所成的角?
1、异面直线
(1)定义:不同在任何一个平面内的两条直线.
(2)异面直线的画法:
2、空间两条直线的位置关系
位置关系 特 点
相交 同一平面内,有且只有一个公共点
平行 同一平面内,没有公共点
异面直线 不同在任何一个平面内,没有公共点
【说明】1、异面直线的定义表明异面直线不具备确定平面的条件;
异面直线既不相交,也不平行;
2、不能把异面直线误认为分别在不同平面内的两条直线,
如图中,虽然有a α,b β,即a,b分别在两个不同的平面内,
但是因为a∩b=O,所以a与b不是异面直线;
3、异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,我们把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角);
(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)当θ=90°时,a与b互相垂直,记作a⊥b.
【说明】异面直线所成角的范围是0°<θ≤90°,所以垂直有两种情况:异面垂直和相交垂直;
例1、如图,在长方体ABCD A1B1C1D1中,
(1)直线A1B与直线D1C的位置关系是________;
(2)直线A1B与直线B1C的位置关系是________;
(3)直线D1D与直线D1C的位置关系是________;
(4)直线AB与直线B1C的位置关系是________.
【提示】注意:理解空间两直线的位置关系及其判断标准;
【答案】(1)平行;(2)异面;(3)相交;(4)异面;
【解析】(1)在长方体ABCD A1B1C1D1中,A1D1∥BC且A1D1=BC,
所以,四边形A1BCD1为平行四边形,所以,A1B∥D1C;
(2)直线A1B与直线B1C不同在任何一个平面内;
(3)直线D1D与直线D1C相交于点D1;
(4)直线AB与直线B1C不同在任何一个平面内;
【说明】本题考查了两直线位置关系的判定;
1、判定两条直线平行或相交的方法:判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断;
2、判定两条直线是异面直线的方法:
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图);
例2、如图所示,已知两个正方形和不在同一平面内,
为的中点;
证明:直线与是异面直线;
【提示】注意:从集合视角理解“已知两个正方形和不在同一平面内”;
假设共面,由此推得∥平面,再求线面平行的性质推得线线平行,
即可退出矛盾;或紧扣判定定理的条件;
【证明】方法1、假设直线与共面,
则平面与平面交于,
又由已知可得////,且,
所以,四边形为平行四边形,则,
又直线不在平面内,直线平面,所以,∥平面,
所以,,所以,∥,这与矛盾,故假设不成立,
所以,与不共面,它们是异面直线;
方法2、因为,点为的中点;
所以,点不在平面,点不在直线上,
所以,由判定定理得直线与是异面直线;
【说明】判定空间两条直线是异面直线的方法:
1、定义法:不同在任何一个平面内的两条直线;
2、判定定理:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线;
3、反证法:证明两线不可能平行、相交或证明两线不可能共面,从而可得两线异面;
例3、在正方体ABCD A1B1C1D1中,E,F分别是A1B1,B1C1的中点,
求异面直线DB1与EF所成角的大小;
【提示】常规方法主要在根据题设“找角”;
【解析】方法1、如图1所示,连接A1C1,B1D1,
并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G,
则OG∥B1D,EF∥A1C1,
∴∠GOA1为异面直线DB1与EF所成的角(或其补角).
∵GA1=GC1,O为A1C1的中点, 图1
∴GO⊥A1C1.
∴异面直线DB1与EF所成的角为90°.
方法2、 如图2所示,连接A1D,取A1D的中点H,连接HE,
则HE綊DB1,于是∠HEF为异面直线DB1与EF所成的角(或其补角).
连接HF,设AA1=1,
则EF=,HE=,
取A1D1的中点I,连接HI,IF, 图2
则HI⊥IF,∴HF2=HI2+IF2=,
∴HF2=EF2+HE2,∴∠HEF=90°.
∴异面直线DB1与EF所成的角为90°;
方法3、如图3,连接A1C1,分别取AA1,CC1的中点M,N,连接MN.
∵E,F分别是A1B1,B1C1的中点,
∴EF∥A1C1,又MN∥A1C1,∴MN∥EF.
连接DM,B1N,MB1,DN,则B1N綊DM,
∴四边形DMB1N为平行四边形,
∴MN与DB1必相交,设交点为P,
则∠DPM为异面直线DB1与EF所成的角(或其补角).
设AA1=k(k>0),则MP=k,DM=k,DP=k, 图3
∴DM2=DP2+MP2,∴∠DPM=90°.
∴异面直线DB1与EF所成的角为90°.
方法4、如图4,在原正方体的右侧补上一个全等的正方体,连接B1Q,易得B1Q∥EF,
∴∠DB1Q就是异面直线DB1与EF所成的角(或其补角).
设AA1=k(k>0),
则B1D=k,DQ=k,B1Q=k,
∴B1D2+B1Q2=DQ2,∴∠DB1Q=90°.
∴异面直线DB1与EF所成的角为90°.
【说明】本题考查了异面直线所成角及其求法;
求两异面直线所成的角的三个步骤
(1)作:根据所成角的定义,用平移法作出异面直线所成的角;
(2)证:证明作出的角就是要求的角;
(3)算:求角的值,常利用解三角形得出;
(4)答:根据题设要求回答;
可用“一作二证三算四答”来概括.同时注意异面直线所成角范围是0°<θ≤90°;
1、对于异面直线的定义的理解
异面直线是不同在任何一个平面内的两条直线.
注意异面直线定义中“任何”两字,它指空间中的所有平面,
因此异面直线也可以理解为:在空间中找不到一个平面,
使其同时经过a,b两条直线.例如,如图所示的长方体中,棱AB和B1C1所在的直线既不平行又不相交,找不到一个平面同时经过这两条棱所在的直线,故AB与B1C1是异面直线.
2、空间两条直线的位置关系
(1)若从有无公共点的角度来看,可分为两类:
直线
(2)若从是否共面的角度看,也可分两类:
直线
3、判定两条直线平行或相交的方法
判定两条直线平行或相交可用平面几何的方法去判断,而两条直线平行也可以用公理4判断.
4、判定两条直线是异面直线的方法
(1)定义法:由定义判断两直线不可能在同一平面内.
(2)判定定理:连接平面内一点与平面外一点的直线,
和这个平面内不经过此点的直线是异面直线;
用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
(3)反证法;
1、如果两条直线a和b没有公共点,那么a与b的位置关系是( )
A.共面 B.平行 C.异面 D.平行或异面
【答案】D;
【解析】空间中两直线的位置关系有:①相交;②平行;③异面.两条直线平行和两条直线异面都满足两条直线没有公共点,故a与b的位置关系是平行或异面.
2、在空间四边形ABCD中,E,F分别为对角线AC,BD的中点,则BE与CF( )
A.平行 B.异面 C.相交 D.以上均有可能
【答案】B;
【解析】假设BE与CF是共面直线,设此平面为α,则E,F,B,C∈α,所以BF,CE α,而A∈CE,D∈BF,所以A,D∈α,即有A,B,C,D∈α,与ABCD为空间四边形矛盾,所以BE与CF是异面直线,故选B.
3、若a,b为异面直线,直线c∥a,则c与b的位置关系是
【答案】异面或相交
【解析】由空间直线的位置关系,知c与b可能异面或相交
4、已知直线a,b,c,下列三个命题:
①若a与b异面,b与c异面,则a与c异面;
②若a∥b,a和c相交,则b和c也相交;
③若a⊥b,a⊥c,则b∥c;
其中,正确命题的个数是
【答案】0;
【解析】①不正确如图;
②不正确,有可能相交也有可能异面;
③不正确.可能平行,可能相交也可能异面.
5、如图所示,正方体ABCD A1B1C1D1中,
E,F分别是棱BC,CC1的中点,
则异面直线EF与B1D1所成的角为__________.
【答案】60°;
【解析】连接BC1,AD1,AB1,
则EF为△BCC1的中位线,
∴EF∥BC1.又∵AB綊CD綊C1D1,
∴四边形ABC1D1为平行四边形.
∴BC1∥AD1.∴EF∥AD1.
∴∠AD1B1为异面直线EF和B1D1所成的角或其补角.
在△AB1D1中,易知AB1=B1D1=AD1,
∴△AB1D1为正三角形,∴∠AD1B1=60°.
∴EF与B1D1所成的角为60°.
6、如图,空间四边形ABCD的对角线AC=8,BD=6,
M,N分别为AB,CD的中点,
并且异面直线AC与BD所成的角为90°,
则MN等于________.
【答案】答案:60°;;
【解析】取AD的中点P,连接PM,PN,
则BD∥PM,AC∥PN,
∴∠MPN即异面直线AC与BD
所成的角,∴∠MPN=90°,
PN=AC=4,PM=BD=3,
∴MN=5.
7、已知A、B、C、D是空间四个点,且直线AB与CD是两条异面直线;
用反证法证明:直线AC与BD也是异面直线.
【提示】根据用反证法证明数学命题的方法和步骤,先假设直线AC、BD是共面直线,再推出错误结论,即可得证;
【解析】假设直线AC、BD是共面直线;
则A,B,C,D四点共面,
所以AB、CD共面,这与AB、CD是异面直线矛盾;
所以假设错误,即直线AC、BD也是异面直线.
8、如图所示,点A是△BCD所在平面外一点,AD=BC,
E,F分别是AB,CD的中点,当EF=AD时,
求:异面直线AD和BC所成的角.
【解析】如图所示,设G为AC的中点,连接EG,FG.
∵E,F,G分别为AB,CD,AC的中点.
∴EG∥BC,且EG=BC;
FG∥AD,且FG=AD.
又AD=BC,∴EG=FG=AD,
∴EG与GF所成的锐角(或直角)即为AD与BC所成的角.
在△EFG中,∵EG=FG=AD,又EF=AD,
∴EG2+FG2=EF2,即EG⊥FG.
∴∠EGF=90°.故AD与BC所成角为90°;
同课章节目录
