2022-2023学年沪科版七年级数学上册 1.2.1数轴 课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年沪科版七年级数学上册 1.2.1数轴 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
1.2.1 数轴
什么是数轴
能说出数轴上的点表示的数
画出数轴并标出给定的数
一、导入
魏武广场站
丹华山庄站
曹氏公园站
N
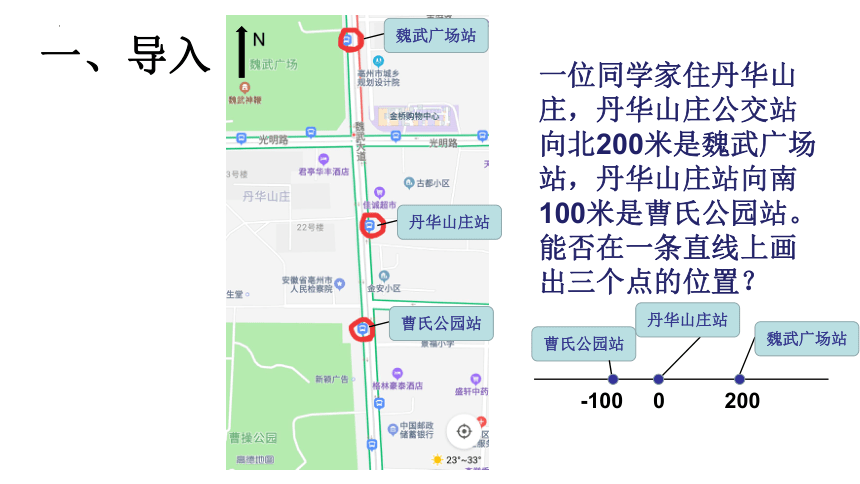
一位同学家住丹华山庄,丹华山庄公交站向北200米是魏武广场站,丹华山庄站向南100米是曹氏公园站。能否在一条直线上画出三个点的位置?
魏武广场站
丹华山庄站
曹氏公园站
-100 0 200
怎么画出来?
-3 -2 -1 0 1 2 3
原点
单位长度
正方向
数轴
二、定义
三要素:原点、正方向、单位长度
原点:画一条直线,任取一点作为原点,表示数0。
正方向:规定直线的一个方向为正方向(右向为正,用箭头 表示)
单位长度:适当的选取某一长度作为单位长度。
数轴:这种规定了原点、正方向和单位长度的直线叫做数轴。
把公交站用数轴表示出来,注意规范。
1 2 3 4 5 6 7
-2 -1 0 1 2 3
-3 -1 0 1 3 5 7
-3 -2 -1 0 1 2 3
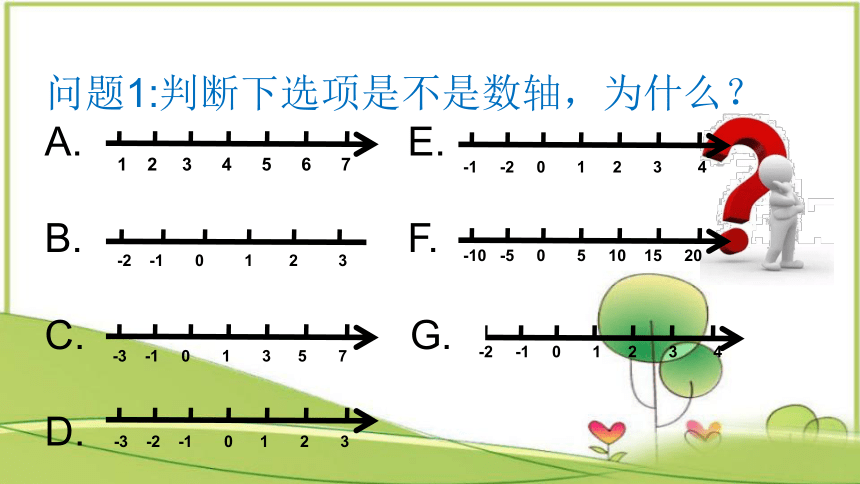
问题1:判断下选项是不是数轴,为什么?
A. E.
B. F.
C. G.
D.
-1 -2 0 1 2 3 4
-10 -5 0 5 10 15 20
-2 -1 0 1 2 3 4
画数轴注意事项:
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻
度均匀.
反思自己画的关于三个站台的数轴是否正确,并修改。
三、运用
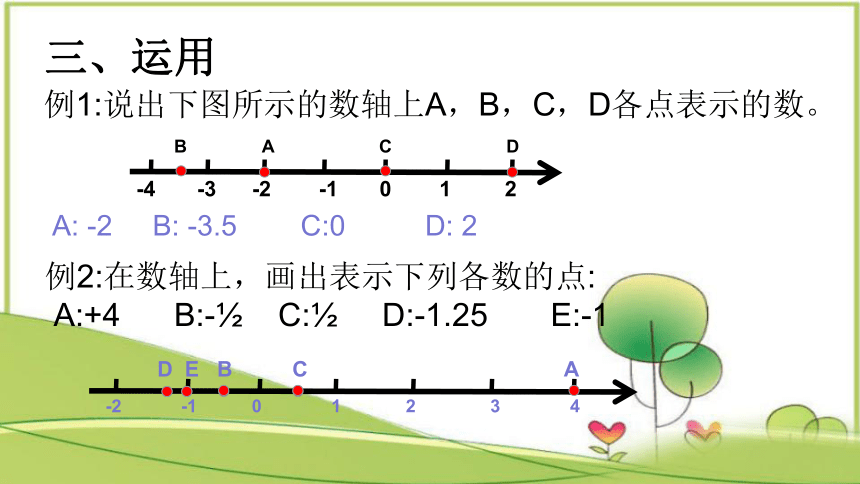
例1:说出下图所示的数轴上A,B,C,D各点表示的数。
A: -2 B: -3.5 C:0 D: 2
-4 -3 -2 -1 0 1 2
B A C D
例2:在数轴上,画出表示下列各数的点:
A:+4 B:- C: D:-1.25 E:-1
-2 -1 0 1 2 3 4
D E B C A
例3 (1)在数轴上,表示-1和3的两点间的距离是多少?
(2)在数轴上,到表示-2的点的距离为3的点表示的数
是多少?
解: 如图所示.在数轴上分别标出表示-1,3,-2的点.
(1)由数轴可知表示-1和3的两点间的距离是4.
(2)由数轴可知到表示-2的点的距离为3的点表示的数是-5或1.
方法点拨:利用数轴可直观的求出两点的距离,由于距离没有方向性,所以到某点距离为某个正值的点一般有两个,因此要注意考虑所有情况.
练一练
1.在数轴上距离原点2.5个单位长度的点所表示的
数是 .
±2.5
2.数轴上一点A,一只蚂蚁从A出发爬了4个单位
长度到了原点,则点A所表示的数是______.
±4
【变式】在数轴上点A表示-4,如果把原点O向负方向移动1.5个单位,那么在新数轴上点A表示的数是( )
A. B.-4 C. -2.5 D.
C
3.在数轴上,老师不小心把一滴墨水滴在画好的数轴上,如图所示,试根据图中标出的数值判断被墨水盖住的整数,并把它写出来.
解:被盖住的数为11,12,13,14,15,16,17,-12,-11,-10,-9,-8.
讨论1:是不是任何一个有理数,都可以用数轴上的一个点来表示。
讨论2:数轴上0左边的数,0右边的数,有什么规律?有没有对应的数?
-2 -1 0 1 2 3 4
D B A C
0左边的数小于0,右边的数大于零。A和B对应,C和D对应,他们数字部分相同,符号不同。并且到原点的距离相等。
任何一个有理数,都可以用数轴上的一个点来表示。有理数与数轴上的点一 一对应。
四、小结
1.学习了什么内容?
2.提高了什么能力?
动手操作能力,数形结合思想,抽象逻辑,直观到理性思维等。
3.还有什么疑问?
应用
画法
定义
一画:
二定:
三选:
四统一:
数轴
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
画直线
定原点
选正方向
统一单位长度
规定了 和 的直线,叫做数轴.
五、作业
1、习题1.2 第4题
在数轴上点A 表示的数是-3,与点A 距离2个单位长度的点表示的数是什么?
2、预习:
带着讨论的第二个问题的答案,预习下节内容。
下课!
数学资料按时完成!
1.2.1 数轴
什么是数轴
能说出数轴上的点表示的数
画出数轴并标出给定的数
一、导入
魏武广场站
丹华山庄站
曹氏公园站
N
一位同学家住丹华山庄,丹华山庄公交站向北200米是魏武广场站,丹华山庄站向南100米是曹氏公园站。能否在一条直线上画出三个点的位置?
魏武广场站
丹华山庄站
曹氏公园站
-100 0 200
怎么画出来?
-3 -2 -1 0 1 2 3
原点
单位长度
正方向
数轴
二、定义
三要素:原点、正方向、单位长度
原点:画一条直线,任取一点作为原点,表示数0。
正方向:规定直线的一个方向为正方向(右向为正,用箭头 表示)
单位长度:适当的选取某一长度作为单位长度。
数轴:这种规定了原点、正方向和单位长度的直线叫做数轴。
把公交站用数轴表示出来,注意规范。
1 2 3 4 5 6 7
-2 -1 0 1 2 3
-3 -1 0 1 3 5 7
-3 -2 -1 0 1 2 3
问题1:判断下选项是不是数轴,为什么?
A. E.
B. F.
C. G.
D.
-1 -2 0 1 2 3 4
-10 -5 0 5 10 15 20
-2 -1 0 1 2 3 4
画数轴注意事项:
(1)原点、单位长度和正方向三要素缺一不可;
(2)直线一般画水平的;
(3)正方向用箭头表示,一般取从左到右;
(4)取单位长度应结合实际需要,但要做到刻
度均匀.
反思自己画的关于三个站台的数轴是否正确,并修改。
三、运用
例1:说出下图所示的数轴上A,B,C,D各点表示的数。
A: -2 B: -3.5 C:0 D: 2
-4 -3 -2 -1 0 1 2
B A C D
例2:在数轴上,画出表示下列各数的点:
A:+4 B:- C: D:-1.25 E:-1
-2 -1 0 1 2 3 4
D E B C A
例3 (1)在数轴上,表示-1和3的两点间的距离是多少?
(2)在数轴上,到表示-2的点的距离为3的点表示的数
是多少?
解: 如图所示.在数轴上分别标出表示-1,3,-2的点.
(1)由数轴可知表示-1和3的两点间的距离是4.
(2)由数轴可知到表示-2的点的距离为3的点表示的数是-5或1.
方法点拨:利用数轴可直观的求出两点的距离,由于距离没有方向性,所以到某点距离为某个正值的点一般有两个,因此要注意考虑所有情况.
练一练
1.在数轴上距离原点2.5个单位长度的点所表示的
数是 .
±2.5
2.数轴上一点A,一只蚂蚁从A出发爬了4个单位
长度到了原点,则点A所表示的数是______.
±4
【变式】在数轴上点A表示-4,如果把原点O向负方向移动1.5个单位,那么在新数轴上点A表示的数是( )
A. B.-4 C. -2.5 D.
C
3.在数轴上,老师不小心把一滴墨水滴在画好的数轴上,如图所示,试根据图中标出的数值判断被墨水盖住的整数,并把它写出来.
解:被盖住的数为11,12,13,14,15,16,17,-12,-11,-10,-9,-8.
讨论1:是不是任何一个有理数,都可以用数轴上的一个点来表示。
讨论2:数轴上0左边的数,0右边的数,有什么规律?有没有对应的数?
-2 -1 0 1 2 3 4
D B A C
0左边的数小于0,右边的数大于零。A和B对应,C和D对应,他们数字部分相同,符号不同。并且到原点的距离相等。
任何一个有理数,都可以用数轴上的一个点来表示。有理数与数轴上的点一 一对应。
四、小结
1.学习了什么内容?
2.提高了什么能力?
动手操作能力,数形结合思想,抽象逻辑,直观到理性思维等。
3.还有什么疑问?
应用
画法
定义
一画:
二定:
三选:
四统一:
数轴
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
画直线
定原点
选正方向
统一单位长度
规定了 和 的直线,叫做数轴.
五、作业
1、习题1.2 第4题
在数轴上点A 表示的数是-3,与点A 距离2个单位长度的点表示的数是什么?
2、预习:
带着讨论的第二个问题的答案,预习下节内容。
下课!
数学资料按时完成!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
