八年级上册数学人教版课时练《11.1.2 三角形的高、中线与角平分线》(word、含答案)
文档属性
| 名称 | 八年级上册数学人教版课时练《11.1.2 三角形的高、中线与角平分线》(word、含答案) | 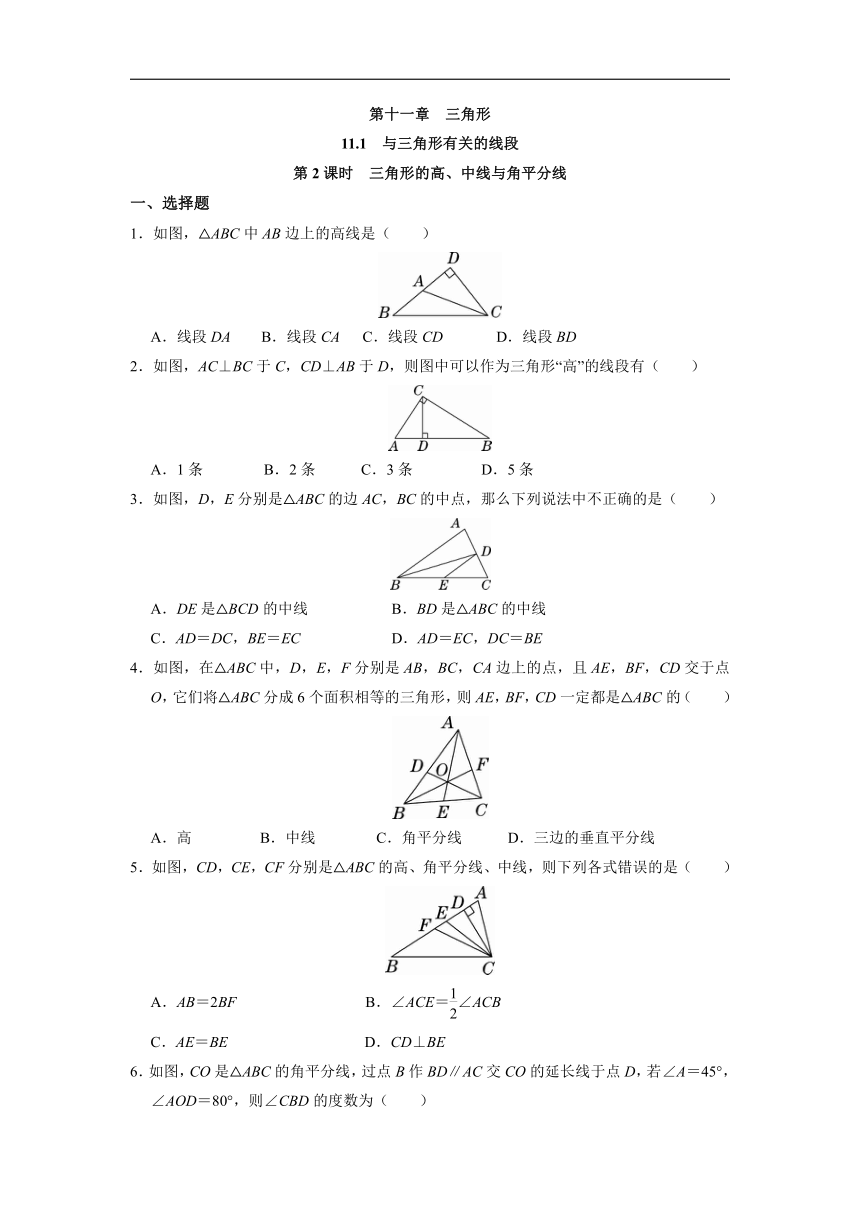 | |
| 格式 | zip | ||
| 文件大小 | 99.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 15:48:23 | ||
图片预览


文档简介
第十一章 三角形
11.1 与三角形有关的线段
第2课时 三角形的高、中线与角平分线
一、选择题
1.如图,△ABC中AB边上的高线是( )
线段DA B.线段CA C.线段CD D.线段BD
2.如图,AC⊥BC于C,CD⊥AB于D,则图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
3.如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.AD=EC,DC=BE
4.如图,在△ABC中,D,E,F分别是AB,BC,CA边上的点,且AE,BF,CD交于点O,它们将△ABC分成6个面积相等的三角形,则AE,BF,CD一定都是△ABC的( )
A.高 B.中线 C.角平分线 D.三边的垂直平分线
5.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式错误的是( )
A.AB=2BF B.∠ACE=∠ACB
C.AE=BE D.CD⊥BE
6.如图,CO是△ABC的角平分线,过点B作BD∥AC交CO的延长线于点D,若∠A=45°,∠AOD=80°,则∠CBD的度数为( )
A.100° B.110° C.125° D.135°
7.如图,已知AD是△ABC的边BC上的中线,CE是△ADC的边AD上的中线,若△ABD的面积为16 cm2,则△ACE的面积为( )
A.32 cm2 B.16 cm2 C.8 cm2 D.4 cm2
8.等腰三角形一腰上的中线把这个三角形的周长分成12 cm和21 cm两部分,则这个等腰三角形底边的长为( )
A.17 cm B.5 cm
C.5 cm或17 cm D.无法确定
9.如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D,点E,点F,△ABC中BC边上的高是( )
A.CF B.BE C.AD D.CD
二、填空题
10.已知在△ABC中,EC平分∠ACB,∠1=∠2,若∠ACE=23°,则∠EDC的度数为________.
11.已知三角形的三边长分别为2,x-3,4,求x的取值范围 .
12.等腰三角形的周长为14,其一边长为4,那么它的底边为 。
13.已知三角形的两边长是3和4,周长是偶数,则这样的三角形的第三边是 .
三、综合题
14.如图,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高;
(2)若△ABD的面积为6,且BD边上的高为3,求BC的长.
15.如图,已知AD,AE分别是△ABC的高和中线,AB=9 cm,AC=12 cm,BC=15 cm,∠BAC=90°.试求:
(1)△ABE的面积;
(2)AD的长度;
(3)△ACE与△ABE的周长的差.
16.如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB于点D,PE⊥AC于点E.若△ABC的面积为14,问:PD+PE的值是否确定?若能确定,则PD+PE的值是多少?若不能确定,请说明理由.
17.如图,D是△ABC的边BC上一点,且BD∶CD=2∶3,E,F分别是线段AD,CE的中点,且△ABC的面积为20 cm2.
求:(1)△CDE的面积;
(2)阴影部分的面积.
参考答案
C
D
D
B
C
B
C
B
C
10.134°
11.54或6
3或5 ;
14.
(1)解:如图所示,AE即为所求.
(2)解:∵AD是△ABC的边BC上的中线,△ABD的面积为6,
∴△ABC的面积为12,
即S△ABC=BC·AE=12.
∵BD边上的高为3,即AE=3,
∴BC=12×2÷3=8.
15.(1)解:27 cm2.
解:AD的长度为 cm.
(3)解:△ACE与△ABE的周长的差为3 cm.
16. 解:PD+PE的值能确定为,.连接AP,
由图(图略)可得S△ABC=S△ABP+S△ACP,
∴14=×8×PD+×8×PE=4(PD+PE).
∴PD+PE=.
17.(1)解:∵△ABD和△ADC等高不等底,BD∶CD=2∶3,
∴S△ABD=S△ABC=×20=8(cm2).
∴S△ADC=20-8=12(cm2).
∵E是线段AD的中点,
∴S△CDE=S△ADC=×12=6(cm2).
(2)解:∵E是线段AD的中点,
∴S△BDE=S△ABD=×8=4(cm2).
由(1)知,S△CDE=6 cm2,
∴S△BCE=S△BDE+S△DCE=4+6=10(cm2).
∵F是线段CE的中点,
∴S△BEF=S△BCE=×10=5(cm2).故阴影部分的面积为5 cm2.
11.1 与三角形有关的线段
第2课时 三角形的高、中线与角平分线
一、选择题
1.如图,△ABC中AB边上的高线是( )
线段DA B.线段CA C.线段CD D.线段BD
2.如图,AC⊥BC于C,CD⊥AB于D,则图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
3.如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
DE是△BCD的中线 B.BD是△ABC的中线
C.AD=DC,BE=EC D.AD=EC,DC=BE
4.如图,在△ABC中,D,E,F分别是AB,BC,CA边上的点,且AE,BF,CD交于点O,它们将△ABC分成6个面积相等的三角形,则AE,BF,CD一定都是△ABC的( )
A.高 B.中线 C.角平分线 D.三边的垂直平分线
5.如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式错误的是( )
A.AB=2BF B.∠ACE=∠ACB
C.AE=BE D.CD⊥BE
6.如图,CO是△ABC的角平分线,过点B作BD∥AC交CO的延长线于点D,若∠A=45°,∠AOD=80°,则∠CBD的度数为( )
A.100° B.110° C.125° D.135°
7.如图,已知AD是△ABC的边BC上的中线,CE是△ADC的边AD上的中线,若△ABD的面积为16 cm2,则△ACE的面积为( )
A.32 cm2 B.16 cm2 C.8 cm2 D.4 cm2
8.等腰三角形一腰上的中线把这个三角形的周长分成12 cm和21 cm两部分,则这个等腰三角形底边的长为( )
A.17 cm B.5 cm
C.5 cm或17 cm D.无法确定
9.如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为点D,点E,点F,△ABC中BC边上的高是( )
A.CF B.BE C.AD D.CD
二、填空题
10.已知在△ABC中,EC平分∠ACB,∠1=∠2,若∠ACE=23°,则∠EDC的度数为________.
11.已知三角形的三边长分别为2,x-3,4,求x的取值范围 .
12.等腰三角形的周长为14,其一边长为4,那么它的底边为 。
13.已知三角形的两边长是3和4,周长是偶数,则这样的三角形的第三边是 .
三、综合题
14.如图,已知AD是△ABC的边BC上的中线.
(1)作出△ABD的边BD上的高;
(2)若△ABD的面积为6,且BD边上的高为3,求BC的长.
15.如图,已知AD,AE分别是△ABC的高和中线,AB=9 cm,AC=12 cm,BC=15 cm,∠BAC=90°.试求:
(1)△ABE的面积;
(2)AD的长度;
(3)△ACE与△ABE的周长的差.
16.如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB于点D,PE⊥AC于点E.若△ABC的面积为14,问:PD+PE的值是否确定?若能确定,则PD+PE的值是多少?若不能确定,请说明理由.
17.如图,D是△ABC的边BC上一点,且BD∶CD=2∶3,E,F分别是线段AD,CE的中点,且△ABC的面积为20 cm2.
求:(1)△CDE的面积;
(2)阴影部分的面积.
参考答案
C
D
D
B
C
B
C
B
C
10.134°
11.5
3或5 ;
14.
(1)解:如图所示,AE即为所求.
(2)解:∵AD是△ABC的边BC上的中线,△ABD的面积为6,
∴△ABC的面积为12,
即S△ABC=BC·AE=12.
∵BD边上的高为3,即AE=3,
∴BC=12×2÷3=8.
15.(1)解:27 cm2.
解:AD的长度为 cm.
(3)解:△ACE与△ABE的周长的差为3 cm.
16. 解:PD+PE的值能确定为,.连接AP,
由图(图略)可得S△ABC=S△ABP+S△ACP,
∴14=×8×PD+×8×PE=4(PD+PE).
∴PD+PE=.
17.(1)解:∵△ABD和△ADC等高不等底,BD∶CD=2∶3,
∴S△ABD=S△ABC=×20=8(cm2).
∴S△ADC=20-8=12(cm2).
∵E是线段AD的中点,
∴S△CDE=S△ADC=×12=6(cm2).
(2)解:∵E是线段AD的中点,
∴S△BDE=S△ABD=×8=4(cm2).
由(1)知,S△CDE=6 cm2,
∴S△BCE=S△BDE+S△DCE=4+6=10(cm2).
∵F是线段CE的中点,
∴S△BEF=S△BCE=×10=5(cm2).故阴影部分的面积为5 cm2.
