微专题 平面与平面所成角的几何解法 讲义-2022-2023学年高二上学期数学沪教版(2020)必修第三册(Word含答案)
文档属性
| 名称 | 微专题 平面与平面所成角的几何解法 讲义-2022-2023学年高二上学期数学沪教版(2020)必修第三册(Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 570.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 18:12:35 | ||
图片预览




文档简介
学生版
带着如下【问题】思考、理解与应用
1、二面角及其平面角的定义;
2、二面角的平面角的作法;
1、二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角(如图);
直线AB叫做二面角的棱,半平面α和β叫做二面角的面;
记法:α AB β,在α,β内,分别取点P,Q时,
可记作P AB Q;当棱记为l时,可记作α l β或P l Q;
(2)二面角的平面角:
①定义:在二面角α l β的棱l上任取一点O,
如图所示,以点O为垂足,在半平面α和β内分别作垂直
于棱l的射线OA和OB,
则射线OA和OB构成的∠AOB叫做二面角的平面角.
②直二面角:平面角是直角的二面角;
2、对于二面角及其平面角的理解
(1)二面角是一个空间图形,而二面角的平面角是平面图形,二面角的大小通过其平面角的大小表示,体现了由空间图形向平面图形转化的思想;
(2)二面角的平面角的定义是两条“射线”的夹角,不是两条直线的夹角,因此,二面角θ的取值范围是0°≤θ≤180°或表示为;
例1、在空间四边形VABC中,
VA=AB=VB=AC=BC=2,VC=,
求:二面角V-AB-C的大小.
【提示】
【解析】
【说明】
例2、如图,在空间四边形SABC中,
∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC;
(1)证明:平面SBC⊥平面SAB;
(2)求二面角A-SC-B的平面角的正弦值;
【提示】
【解析】
【说明】本题主要考查了利用三垂线定理找二面角的平面角;
三垂线法:是利用三垂线定理及其逆定理来证明线线垂直,来找到二面角的平面角的方法;
这种方法关键是找垂直于二面角的面的垂线.此方法是属于较常用的;
三垂线定理:在平面内的一条直线如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直;
三垂线定理的逆定理:在平面内的一条直线如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直;
例3、如图,在空间四边形SABC中,
SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于点D,E,
又SA=AB,SB=BC,
求二面角E-BD-C的大小.
【说明】本题考查了通过做二面角的棱的垂直的方法,间接找二面角的平面角的方法;
垂面法:作一与棱垂直的平面,该垂面与二面角两半平面相交,得到交线,交线所成的角为二面角的平面角.关键在找与二面角的棱垂直且与二面角两半平面都有交线的平面;
二面角是立体几何中最重要的知识点,是高考的热点和重点.求二面角的常见方法有定义法,三垂线法,垂面法.
解决二面角问题的策略:清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点;求二面角的大小的方法为:一作,即先作出二面角的平面角;二证,即说明所作角是二面角的平面角;三求,即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”;
1、从空间一点P向二面角α l β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角α l β的平面角的大小是( )
A.60° B.120° C.60°或120° D.不确定
2、如图所示,将等腰直角三角形ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( )
A.30°
B.45°
C.60°
D.90°
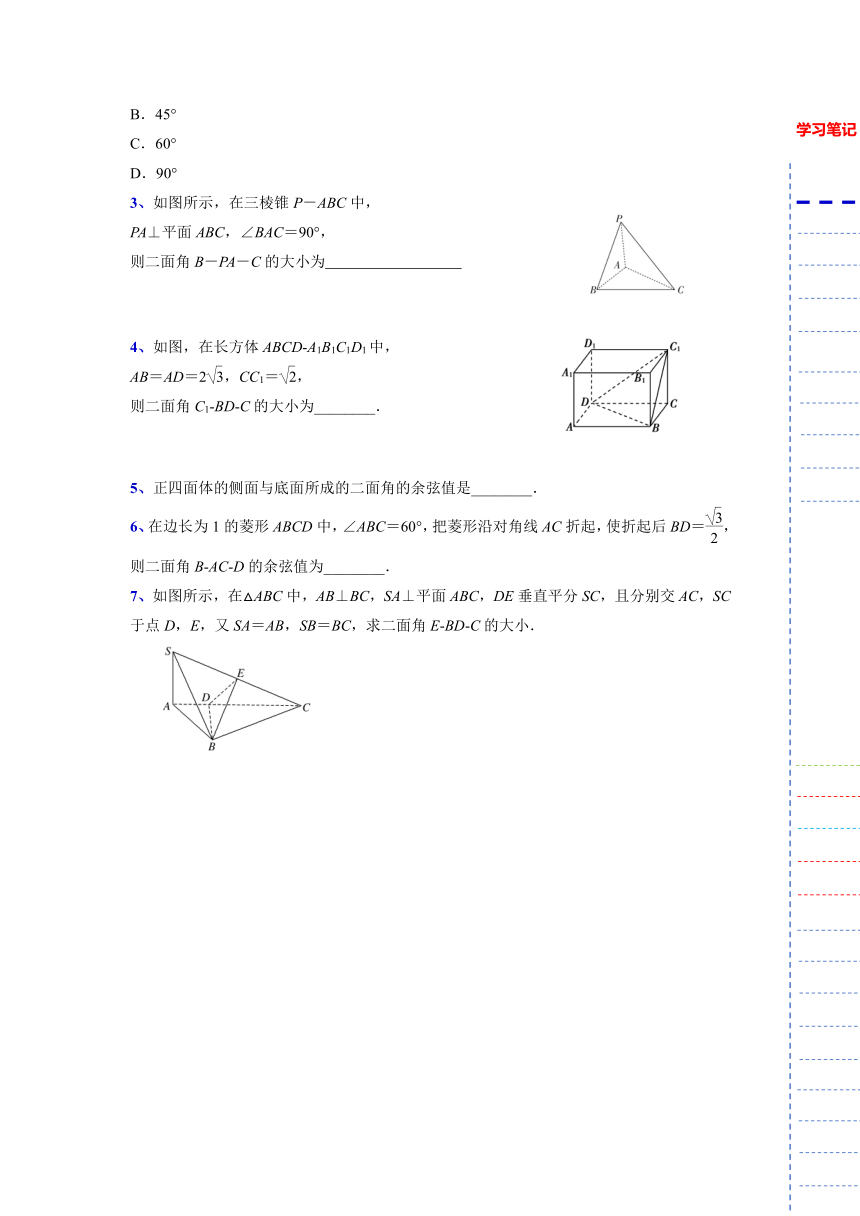
3、如图所示,在三棱锥P-ABC中,
PA⊥平面ABC,∠BAC=90°,
则二面角B-PA-C的大小为
4、如图,在长方体ABCD A1B1C1D1中,
AB=AD=2,CC1=,
则二面角C1 BD C的大小为________.
5、正四面体的侧面与底面所成的二面角的余弦值是________.
6、在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=,则二面角B AC D的余弦值为________.
7、如图所示,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC,SC于点D,E,又SA=AB,SB=BC,求二面角E BD C的大小.
【说明】作二面角的平面角的方法:作二面角的平面角可以用定义法,也可以用垂面法,即在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
8、如图,在四棱锥P-ABCD中,底面ABCD为四边形,
△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,
平面PBD⊥平面ABCD;
(1)求证:PD⊥平面ABCD;
(2)若二面角C-PB-D的平面角的余弦值为,求PD的长;
.
教师版
带着如下【问题】思考、理解与应用
1、二面角及其平面角的定义;
2、二面角的平面角的作法;
1、二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角(如图);
直线AB叫做二面角的棱,半平面α和β叫做二面角的面;
记法:α AB β,在α,β内,分别取点P,Q时,
可记作P AB Q;当棱记为l时,可记作α l β或P l Q;
(2)二面角的平面角:
①定义:在二面角α l β的棱l上任取一点O,
如图所示,以点O为垂足,在半平面α和β内分别作垂直
于棱l的射线OA和OB,
则射线OA和OB构成的∠AOB叫做二面角的平面角.
②直二面角:平面角是直角的二面角;
2、对于二面角及其平面角的理解
(1)二面角是一个空间图形,而二面角的平面角是平面图形,二面角的大小通过其平面角的大小表示,体现了由空间图形向平面图形转化的思想;
(2)二面角的平面角的定义是两条“射线”的夹角,不是两条直线的夹角,因此,二面角θ的取值范围是0°≤θ≤180°或表示为;
例1、在空间四边形VABC中,
VA=AB=VB=AC=BC=2,VC=,
求:二面角V-AB-C的大小.
【提示】注意根据“对称性”找平面角;
【解析】取AB的中点D,
连接VD,CD,
因为,△VAB中,VA=VB=AB=2,
所以,△VAB为等边三角形,
所以,VD⊥AB且VD=,
同理CD⊥AB,CD=,
所以,∠VDC为二面角V-AB-C的平面角,
而△VDC是等边三角形,∠VDC=60°,
所以,二面角V-AB-C的大小为60°;
【说明】本题考查了利用“定义法”求二面角;定义法:利用二面角的平面角的定义,在二面角的棱上取一点,过该点在两个半平面内作垂直于棱的射线,两射线所成的角就是二面角的平面角,这是一种最基本的方法;
例2、如图,在空间四边形SABC中,
∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC;
(1)证明:平面SBC⊥平面SAB;
(2)求二面角A-SC-B的平面角的正弦值;
【提示】注意角“90°”与垂直的关联;
【解析】(1)证明:因为,∠SAB=∠SAC=90°,所以,SA⊥AB,SA⊥AC,
又AB∩AC=A,AB,AC 平面ABC,
所以,SA⊥平面ABC,
又BC 平面ABC,∴SA⊥BC,
又AB⊥BC,SA∩AB=A,SA,AB 平面SAB,
所以,BC⊥平面SAB,
又BC 平面SBC,∴平面SBC⊥平面SAB.
(2)解:取SB的中点D,连接AD,则AD⊥SB,垂足为点D,
由(1)知平面SBC⊥平面SAB,平面SBC∩平面SAB=SB,AD 平面SAB,
所以,AD⊥平面SBC.
作AE⊥SC,垂足为点E,连接DE,
则DE⊥SC,
则∠AED为二面角A-SC-B的平面角.
设SA=AB=2,则SB=BC=2,AD=,AC=2,SC=4.
由题意得AE=,
Rt△ADE中,sin∠AED===,
所以,二面角A-SC-B的平面角的正弦值为;
【说明】本题主要考查了利用三垂线定理找二面角的平面角;
三垂线法:是利用三垂线定理及其逆定理来证明线线垂直,来找到二面角的平面角的方法;
这种方法关键是找垂直于二面角的面的垂线.此方法是属于较常用的;
三垂线定理:在平面内的一条直线如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直;
三垂线定理的逆定理:在平面内的一条直线如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直;
例3、如图,在空间四边形SABC中,
SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于点D,E,
又SA=AB,SB=BC,
求二面角E-BD-C的大小.
【提示】注意用好题设“SA⊥底面ABC”;
【解析】因为,SB=BC且E是SC的中点,
所以,BE是等腰三角形SBC底边SC的中线,∴SC⊥BE.
又已知SC⊥DE,BE∩DE=E,BE,DE 平面BDE,
所以,SC⊥平面BDE,所以,SC⊥BD;
又SA⊥平面ABC,BD 平面ABC,
所以,SA⊥BD,而SC∩SA=S,SC,SA 平面SAC,
所以,BD⊥平面SAC;
因为,平面SAC∩平面BDE=DE,
平面SAC∩平面BDC=DC,
所以,BD⊥DE,BD⊥DC,
所以,∠EDC是所求二面角的平面角;
因为,SA⊥底面ABC,∴SA⊥AB,SA⊥AC,
设SA=2,则AB=2,BC=SB=2,
因为,AB⊥BC,所以,AC=2,所以,∠ACS=30°;
又已知DE⊥SC,所以,∠EDC=60°;
即所求的二面角等于60°;
【说明】本题考查了通过做二面角的棱的垂直的方法,间接找二面角的平面角的方法;
垂面法:作一与棱垂直的平面,该垂面与二面角两半平面相交,得到交线,交线所成的角为二面角的平面角.关键在找与二面角的棱垂直且与二面角两半平面都有交线的平面;
二面角是立体几何中最重要的知识点,是高考的热点和重点.求二面角的常见方法有定义法,三垂线法,垂面法.
解决二面角问题的策略:清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点;求二面角的大小的方法为:一作,即先作出二面角的平面角;二证,即说明所作角是二面角的平面角;三求,即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”;
1、从空间一点P向二面角α l β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角α l β的平面角的大小是( )
A.60° B.120° C.60°或120° D.不确定
【答案】C;
【解析】若点P在二面角内,则二面角的平面角为120°;若点P在二面角外,则二面角的平面角为60°;
2、如图所示,将等腰直角三角形ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( )
A.30°
B.45°
C.60°
D.90°
【答案】D;
【解析】连结B′C,则△AB′C为等边三角形,
设AD=a,
则B′C=AC=a,B′D=DC=a,
所以B′C2=B′D2+DC2,
所以∠B′DC=90°;
3、如图所示,在三棱锥P-ABC中,
PA⊥平面ABC,∠BAC=90°,
则二面角B-PA-C的大小为
【答案】90°;
【解析】∵PA⊥平面ABC,BA,CA 平面ABC,∴BA⊥PA,CA⊥PA,因此∠BAC即为二面角B-PA-C的平面角.又∠BAC=90°;
4、如图,在长方体ABCD A1B1C1D1中,
AB=AD=2,CC1=,
则二面角C1 BD C的大小为________.
【答案】30°;
【解析】如图,取BD中点O,连结OC,OC1.
∵AB=AD=2,∴CO⊥BD,CO=.
∵CD=BC,∴C1D=C1B,∴C1O⊥BD.
∴∠C1OC为二面角C1 BD C的平面角,
∴tan∠C1OC===,
∴∠C1OC=30°,即二面角C1 BD C的大小为30°;
5、正四面体的侧面与底面所成的二面角的余弦值是________.
【答案】;
【解析】如图所示,设正四面体A BCD的棱长为1,
顶点A在底面上的射影为O,连接DO,并延长交BC于点E,
连接AE,则E为BC的中点,故AE⊥BC,DE⊥BC,
∴∠AEO为侧面ABC与底面BCD所成的二面角的平面角.
在Rt△AEO中,AE=,EO=ED=×=,
∴cos∠AEO==;
6、在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=,则二面角B AC D的余弦值为________.
【答案】60°;
【解析】如图所示,由二面角的定义知∠BOD即为二面角的平面角.
∵DO=OB=BD=,
∴∠BOD=60°;
7、如图所示,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC,SC于点D,E,又SA=AB,SB=BC,求二面角E BD C的大小.
【解析】∵E为SC中点,且SB=BC,
∴BE⊥SC.又DE⊥SC,
BE∩DE=E,∴SC⊥平面BDE,
∴BD⊥SC.又SA⊥平面ABC,
可得SA⊥BD,SC∩SA=S,
∴BD⊥平面SAC,从而BD⊥AC,BD⊥DE,
∴∠EDC为二面角E BD C的平面角.
设SA=AB=1,在△ABC中,∵AB⊥BC,∴SB=BC=,
AC=,∴SC=2.在Rt△SAC中,∠DCS=30°,
∴∠EDC=60°,即二面角E BD C为60°.
【说明】作二面角的平面角的方法:作二面角的平面角可以用定义法,也可以用垂面法,即在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
8、如图,在四棱锥P-ABCD中,底面ABCD为四边形,
△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,
平面PBD⊥平面ABCD;
(1)求证:PD⊥平面ABCD;
(2)若二面角C-PB-D的平面角的余弦值为,求PD的长;
【解析】(1)证明 如图所示,E为BD的中点,连接AE,△ABD是正三角形,
则AE⊥BD.
平面PBD⊥平面ABCD,平面PBD∩平面ABCD=BD,
AE 平面ABCD,
故AE⊥平面PBD,PD 平面PBD,
故AE⊥PD.
PD⊥AB,AE∩AB=A,
AE,AB 平面ABCD,
故PD⊥平面ABCD.
(2)解 过点E作EF⊥PB于点F,连接CF,CE,
因为BC⊥CD,BC=CD,E为BD的中点,
所以EC⊥BD,
所以EC⊥平面PBD.
又PB 平面PBD,所以EC⊥PB,
又EC∩EF=E,EC,EF 平面EFC,
所以PB⊥平面EFC,
又因为CF 平面EFC,
所以CF⊥PB,
故∠EFC为二面角C-PB-D的平面角.
cos∠EFC=,
故tan∠EFC=,EC=1,故EF=.
sin∠PBD==,tan∠PBD=,
即=,PD=1.
【说明】解决二面角问题的策略:清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点.求二面角的大小的方法为:一作,即先作出二面角的平面角;二证,即说明所作角是二面角的平面角;三求,即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”.
带着如下【问题】思考、理解与应用
1、二面角及其平面角的定义;
2、二面角的平面角的作法;
1、二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角(如图);
直线AB叫做二面角的棱,半平面α和β叫做二面角的面;
记法:α AB β,在α,β内,分别取点P,Q时,
可记作P AB Q;当棱记为l时,可记作α l β或P l Q;
(2)二面角的平面角:
①定义:在二面角α l β的棱l上任取一点O,
如图所示,以点O为垂足,在半平面α和β内分别作垂直
于棱l的射线OA和OB,
则射线OA和OB构成的∠AOB叫做二面角的平面角.
②直二面角:平面角是直角的二面角;
2、对于二面角及其平面角的理解
(1)二面角是一个空间图形,而二面角的平面角是平面图形,二面角的大小通过其平面角的大小表示,体现了由空间图形向平面图形转化的思想;
(2)二面角的平面角的定义是两条“射线”的夹角,不是两条直线的夹角,因此,二面角θ的取值范围是0°≤θ≤180°或表示为;
例1、在空间四边形VABC中,
VA=AB=VB=AC=BC=2,VC=,
求:二面角V-AB-C的大小.
【提示】
【解析】
【说明】
例2、如图,在空间四边形SABC中,
∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC;
(1)证明:平面SBC⊥平面SAB;
(2)求二面角A-SC-B的平面角的正弦值;
【提示】
【解析】
【说明】本题主要考查了利用三垂线定理找二面角的平面角;
三垂线法:是利用三垂线定理及其逆定理来证明线线垂直,来找到二面角的平面角的方法;
这种方法关键是找垂直于二面角的面的垂线.此方法是属于较常用的;
三垂线定理:在平面内的一条直线如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直;
三垂线定理的逆定理:在平面内的一条直线如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直;
例3、如图,在空间四边形SABC中,
SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于点D,E,
又SA=AB,SB=BC,
求二面角E-BD-C的大小.
【说明】本题考查了通过做二面角的棱的垂直的方法,间接找二面角的平面角的方法;
垂面法:作一与棱垂直的平面,该垂面与二面角两半平面相交,得到交线,交线所成的角为二面角的平面角.关键在找与二面角的棱垂直且与二面角两半平面都有交线的平面;
二面角是立体几何中最重要的知识点,是高考的热点和重点.求二面角的常见方法有定义法,三垂线法,垂面法.
解决二面角问题的策略:清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点;求二面角的大小的方法为:一作,即先作出二面角的平面角;二证,即说明所作角是二面角的平面角;三求,即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”;
1、从空间一点P向二面角α l β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角α l β的平面角的大小是( )
A.60° B.120° C.60°或120° D.不确定
2、如图所示,将等腰直角三角形ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( )
A.30°
B.45°
C.60°
D.90°
3、如图所示,在三棱锥P-ABC中,
PA⊥平面ABC,∠BAC=90°,
则二面角B-PA-C的大小为
4、如图,在长方体ABCD A1B1C1D1中,
AB=AD=2,CC1=,
则二面角C1 BD C的大小为________.
5、正四面体的侧面与底面所成的二面角的余弦值是________.
6、在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=,则二面角B AC D的余弦值为________.
7、如图所示,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC,SC于点D,E,又SA=AB,SB=BC,求二面角E BD C的大小.
【说明】作二面角的平面角的方法:作二面角的平面角可以用定义法,也可以用垂面法,即在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
8、如图,在四棱锥P-ABCD中,底面ABCD为四边形,
△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,
平面PBD⊥平面ABCD;
(1)求证:PD⊥平面ABCD;
(2)若二面角C-PB-D的平面角的余弦值为,求PD的长;
.
教师版
带着如下【问题】思考、理解与应用
1、二面角及其平面角的定义;
2、二面角的平面角的作法;
1、二面角
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角(如图);
直线AB叫做二面角的棱,半平面α和β叫做二面角的面;
记法:α AB β,在α,β内,分别取点P,Q时,
可记作P AB Q;当棱记为l时,可记作α l β或P l Q;
(2)二面角的平面角:
①定义:在二面角α l β的棱l上任取一点O,
如图所示,以点O为垂足,在半平面α和β内分别作垂直
于棱l的射线OA和OB,
则射线OA和OB构成的∠AOB叫做二面角的平面角.
②直二面角:平面角是直角的二面角;
2、对于二面角及其平面角的理解
(1)二面角是一个空间图形,而二面角的平面角是平面图形,二面角的大小通过其平面角的大小表示,体现了由空间图形向平面图形转化的思想;
(2)二面角的平面角的定义是两条“射线”的夹角,不是两条直线的夹角,因此,二面角θ的取值范围是0°≤θ≤180°或表示为;
例1、在空间四边形VABC中,
VA=AB=VB=AC=BC=2,VC=,
求:二面角V-AB-C的大小.
【提示】注意根据“对称性”找平面角;
【解析】取AB的中点D,
连接VD,CD,
因为,△VAB中,VA=VB=AB=2,
所以,△VAB为等边三角形,
所以,VD⊥AB且VD=,
同理CD⊥AB,CD=,
所以,∠VDC为二面角V-AB-C的平面角,
而△VDC是等边三角形,∠VDC=60°,
所以,二面角V-AB-C的大小为60°;
【说明】本题考查了利用“定义法”求二面角;定义法:利用二面角的平面角的定义,在二面角的棱上取一点,过该点在两个半平面内作垂直于棱的射线,两射线所成的角就是二面角的平面角,这是一种最基本的方法;
例2、如图,在空间四边形SABC中,
∠SAB=∠SAC=∠ABC=90°,SA=AB,SB=BC;
(1)证明:平面SBC⊥平面SAB;
(2)求二面角A-SC-B的平面角的正弦值;
【提示】注意角“90°”与垂直的关联;
【解析】(1)证明:因为,∠SAB=∠SAC=90°,所以,SA⊥AB,SA⊥AC,
又AB∩AC=A,AB,AC 平面ABC,
所以,SA⊥平面ABC,
又BC 平面ABC,∴SA⊥BC,
又AB⊥BC,SA∩AB=A,SA,AB 平面SAB,
所以,BC⊥平面SAB,
又BC 平面SBC,∴平面SBC⊥平面SAB.
(2)解:取SB的中点D,连接AD,则AD⊥SB,垂足为点D,
由(1)知平面SBC⊥平面SAB,平面SBC∩平面SAB=SB,AD 平面SAB,
所以,AD⊥平面SBC.
作AE⊥SC,垂足为点E,连接DE,
则DE⊥SC,
则∠AED为二面角A-SC-B的平面角.
设SA=AB=2,则SB=BC=2,AD=,AC=2,SC=4.
由题意得AE=,
Rt△ADE中,sin∠AED===,
所以,二面角A-SC-B的平面角的正弦值为;
【说明】本题主要考查了利用三垂线定理找二面角的平面角;
三垂线法:是利用三垂线定理及其逆定理来证明线线垂直,来找到二面角的平面角的方法;
这种方法关键是找垂直于二面角的面的垂线.此方法是属于较常用的;
三垂线定理:在平面内的一条直线如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直;
三垂线定理的逆定理:在平面内的一条直线如果和这个平面的一条斜线垂直,那么它和这条斜线的射影垂直;
例3、如图,在空间四边形SABC中,
SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC,SC于点D,E,
又SA=AB,SB=BC,
求二面角E-BD-C的大小.
【提示】注意用好题设“SA⊥底面ABC”;
【解析】因为,SB=BC且E是SC的中点,
所以,BE是等腰三角形SBC底边SC的中线,∴SC⊥BE.
又已知SC⊥DE,BE∩DE=E,BE,DE 平面BDE,
所以,SC⊥平面BDE,所以,SC⊥BD;
又SA⊥平面ABC,BD 平面ABC,
所以,SA⊥BD,而SC∩SA=S,SC,SA 平面SAC,
所以,BD⊥平面SAC;
因为,平面SAC∩平面BDE=DE,
平面SAC∩平面BDC=DC,
所以,BD⊥DE,BD⊥DC,
所以,∠EDC是所求二面角的平面角;
因为,SA⊥底面ABC,∴SA⊥AB,SA⊥AC,
设SA=2,则AB=2,BC=SB=2,
因为,AB⊥BC,所以,AC=2,所以,∠ACS=30°;
又已知DE⊥SC,所以,∠EDC=60°;
即所求的二面角等于60°;
【说明】本题考查了通过做二面角的棱的垂直的方法,间接找二面角的平面角的方法;
垂面法:作一与棱垂直的平面,该垂面与二面角两半平面相交,得到交线,交线所成的角为二面角的平面角.关键在找与二面角的棱垂直且与二面角两半平面都有交线的平面;
二面角是立体几何中最重要的知识点,是高考的热点和重点.求二面角的常见方法有定义法,三垂线法,垂面法.
解决二面角问题的策略:清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点;求二面角的大小的方法为:一作,即先作出二面角的平面角;二证,即说明所作角是二面角的平面角;三求,即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”;
1、从空间一点P向二面角α l β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角α l β的平面角的大小是( )
A.60° B.120° C.60°或120° D.不确定
【答案】C;
【解析】若点P在二面角内,则二面角的平面角为120°;若点P在二面角外,则二面角的平面角为60°;
2、如图所示,将等腰直角三角形ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( )
A.30°
B.45°
C.60°
D.90°
【答案】D;
【解析】连结B′C,则△AB′C为等边三角形,
设AD=a,
则B′C=AC=a,B′D=DC=a,
所以B′C2=B′D2+DC2,
所以∠B′DC=90°;
3、如图所示,在三棱锥P-ABC中,
PA⊥平面ABC,∠BAC=90°,
则二面角B-PA-C的大小为
【答案】90°;
【解析】∵PA⊥平面ABC,BA,CA 平面ABC,∴BA⊥PA,CA⊥PA,因此∠BAC即为二面角B-PA-C的平面角.又∠BAC=90°;
4、如图,在长方体ABCD A1B1C1D1中,
AB=AD=2,CC1=,
则二面角C1 BD C的大小为________.
【答案】30°;
【解析】如图,取BD中点O,连结OC,OC1.
∵AB=AD=2,∴CO⊥BD,CO=.
∵CD=BC,∴C1D=C1B,∴C1O⊥BD.
∴∠C1OC为二面角C1 BD C的平面角,
∴tan∠C1OC===,
∴∠C1OC=30°,即二面角C1 BD C的大小为30°;
5、正四面体的侧面与底面所成的二面角的余弦值是________.
【答案】;
【解析】如图所示,设正四面体A BCD的棱长为1,
顶点A在底面上的射影为O,连接DO,并延长交BC于点E,
连接AE,则E为BC的中点,故AE⊥BC,DE⊥BC,
∴∠AEO为侧面ABC与底面BCD所成的二面角的平面角.
在Rt△AEO中,AE=,EO=ED=×=,
∴cos∠AEO==;
6、在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=,则二面角B AC D的余弦值为________.
【答案】60°;
【解析】如图所示,由二面角的定义知∠BOD即为二面角的平面角.
∵DO=OB=BD=,
∴∠BOD=60°;
7、如图所示,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC,SC于点D,E,又SA=AB,SB=BC,求二面角E BD C的大小.
【解析】∵E为SC中点,且SB=BC,
∴BE⊥SC.又DE⊥SC,
BE∩DE=E,∴SC⊥平面BDE,
∴BD⊥SC.又SA⊥平面ABC,
可得SA⊥BD,SC∩SA=S,
∴BD⊥平面SAC,从而BD⊥AC,BD⊥DE,
∴∠EDC为二面角E BD C的平面角.
设SA=AB=1,在△ABC中,∵AB⊥BC,∴SB=BC=,
AC=,∴SC=2.在Rt△SAC中,∠DCS=30°,
∴∠EDC=60°,即二面角E BD C为60°.
【说明】作二面角的平面角的方法:作二面角的平面角可以用定义法,也可以用垂面法,即在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
8、如图,在四棱锥P-ABCD中,底面ABCD为四边形,
△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,
平面PBD⊥平面ABCD;
(1)求证:PD⊥平面ABCD;
(2)若二面角C-PB-D的平面角的余弦值为,求PD的长;
【解析】(1)证明 如图所示,E为BD的中点,连接AE,△ABD是正三角形,
则AE⊥BD.
平面PBD⊥平面ABCD,平面PBD∩平面ABCD=BD,
AE 平面ABCD,
故AE⊥平面PBD,PD 平面PBD,
故AE⊥PD.
PD⊥AB,AE∩AB=A,
AE,AB 平面ABCD,
故PD⊥平面ABCD.
(2)解 过点E作EF⊥PB于点F,连接CF,CE,
因为BC⊥CD,BC=CD,E为BD的中点,
所以EC⊥BD,
所以EC⊥平面PBD.
又PB 平面PBD,所以EC⊥PB,
又EC∩EF=E,EC,EF 平面EFC,
所以PB⊥平面EFC,
又因为CF 平面EFC,
所以CF⊥PB,
故∠EFC为二面角C-PB-D的平面角.
cos∠EFC=,
故tan∠EFC=,EC=1,故EF=.
sin∠PBD==,tan∠PBD=,
即=,PD=1.
【说明】解决二面角问题的策略:清楚二面角的平面角的大小与顶点在棱上的位置无关,通常可根据需要选择特殊点作平面角的顶点.求二面角的大小的方法为:一作,即先作出二面角的平面角;二证,即说明所作角是二面角的平面角;三求,即利用二面角的平面角所在的三角形算出角的三角函数值,其中关键是“作”.
同课章节目录
