2022—2023学年北师大版数学八年级上册1.1.2探索勾股定理(二)课件 (共13张PPT)
文档属性
| 名称 | 2022—2023学年北师大版数学八年级上册1.1.2探索勾股定理(二)课件 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 880.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第一章 勾股定理
1.1.2 探索勾股定理
授课人:fb
温故知新
勾股定理:
(1)文字语言:
A
B
C
a
b
c
(2)符号语言:
(已知)
(勾股定理)
直角三角形两直角边的平方和等于斜边的平方。
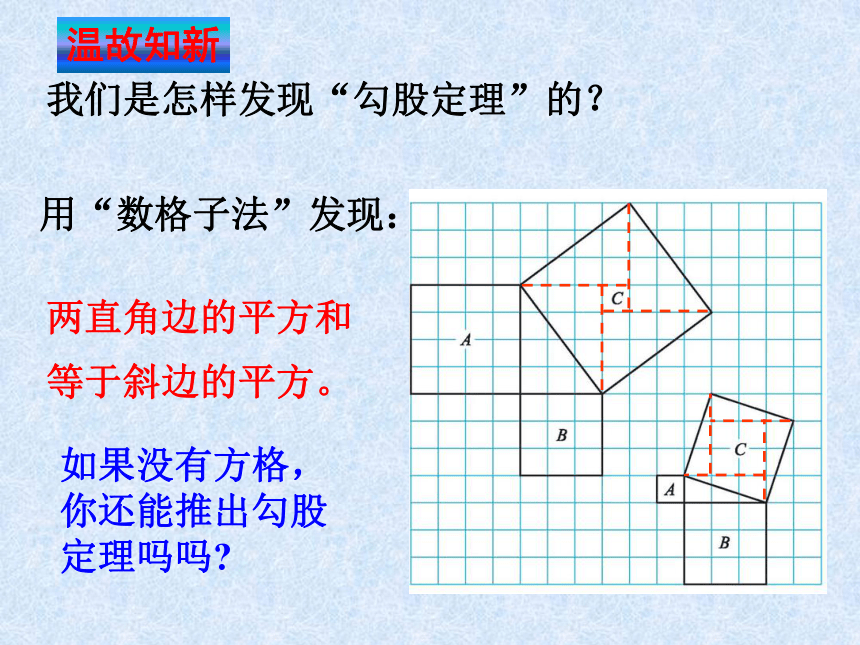
我们是怎样发现“勾股定理”的?
用“数格子法”发现:
温故知新
如果没有方格,你还能推出勾股定理吗吗
两直角边的平方和等于斜边的平方。
一、内嵌法:
b-a
a
b
c
你还有其它的拼图方法吗
正方形面积可表示为:
或者
新知探究:
新知探究:
大正方形ABCD的面积可以表示为:
或者
a
b
c
┛
D
A
B
C
二、外镶法
你还有其它的拼图方法吗
a
b
c
例1、我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
400米
500米
A
公路
B
C
解:
┛
由勾股定理得
敌方汽车 10 s行驶了 300 m,
那么它 1 h 行驶的距离=
300
×6
×60
=108000(m)
=108(km)
即它行驶的速度为108 km / h.
判断图中三角形的三边长是否满足a2+b2=c2
9
8
29
9
8
5
议一议:
数学理解
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?
“总统证明法”
b
a
c
┛
b
a
c
┛
┛
青入
青出
刘徽“青朱出入图
朱出
朱入
朱出
朱入
2.一个直角三角形的斜边为20cm ,且两直角边长度比为3:4,求两直角边的长。
3.如图,受台风麦莎影响,一棵高18米的大树断裂,树的顶部落在离树根底部6 m处,这棵树折断后有多高?
6 m
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么 .
思想 1. 数形结合思想
2. 方程的思想
小结
作业:P6-7
1,2,3
第一章 勾股定理
1.1.2 探索勾股定理
授课人:fb
温故知新
勾股定理:
(1)文字语言:
A
B
C
a
b
c
(2)符号语言:
(已知)
(勾股定理)
直角三角形两直角边的平方和等于斜边的平方。
我们是怎样发现“勾股定理”的?
用“数格子法”发现:
温故知新
如果没有方格,你还能推出勾股定理吗吗
两直角边的平方和等于斜边的平方。
一、内嵌法:
b-a
a
b
c
你还有其它的拼图方法吗
正方形面积可表示为:
或者
新知探究:
新知探究:
大正方形ABCD的面积可以表示为:
或者
a
b
c
┛
D
A
B
C
二、外镶法
你还有其它的拼图方法吗
a
b
c
例1、我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
400米
500米
A
公路
B
C
解:
┛
由勾股定理得
敌方汽车 10 s行驶了 300 m,
那么它 1 h 行驶的距离=
300
×6
×60
=108000(m)
=108(km)
即它行驶的速度为108 km / h.
判断图中三角形的三边长是否满足a2+b2=c2
9
8
29
9
8
5
议一议:
数学理解
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?
“总统证明法”
b
a
c
┛
b
a
c
┛
┛
青入
青出
刘徽“青朱出入图
朱出
朱入
朱出
朱入
2.一个直角三角形的斜边为20cm ,且两直角边长度比为3:4,求两直角边的长。
3.如图,受台风麦莎影响,一棵高18米的大树断裂,树的顶部落在离树根底部6 m处,这棵树折断后有多高?
6 m
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么 .
思想 1. 数形结合思想
2. 方程的思想
小结
作业:P6-7
1,2,3
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
