2022—2023学年人教版数学九年级上册22.1.1 二次函数 课件 (共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册22.1.1 二次函数 课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 09:42:16 | ||
图片预览




文档简介
(共17张PPT)
22.1.1 二次函数
基础回顾 什么叫函数
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。x叫自变量,y叫x的函数。 。
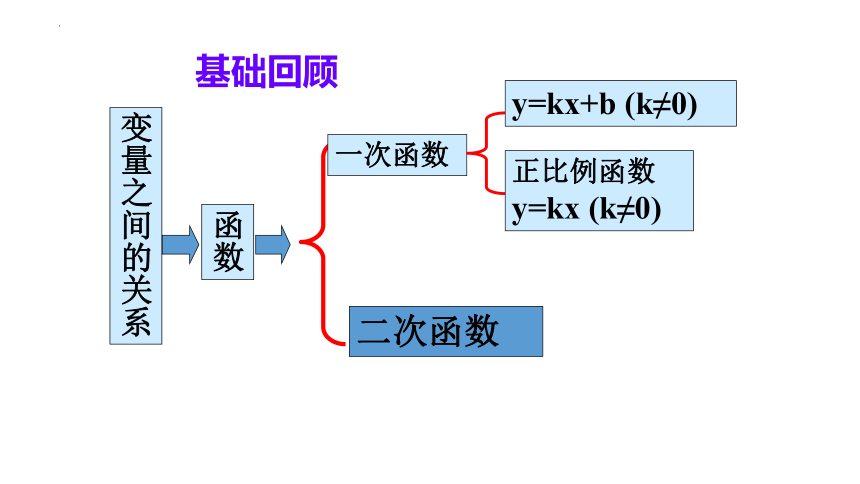
目前,我们已经学习了那几种类型的函数?
二次函数
变量之间的关系
函数
一次函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
基础回顾
观察篮球运动轨迹
讨论与思考:
1、正方形的六个面是全等的正方形,设正方体的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,他们的具体关系是可以表示为什么?
2、多边形的对角线数d与边数n有什么关系?
y=6x2
d= n(n-3)
1
2
d= n2- n
1
2
3
2
即
x
3、某工厂一种产品现在的年产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
y=20(1+x)2
y=20x2+40x+20
即
y=6x2
d= n2- n
1
2
3
2
y=20x2+40x+20
自变量
函数
函数解析式
y
y
d
x
x
n
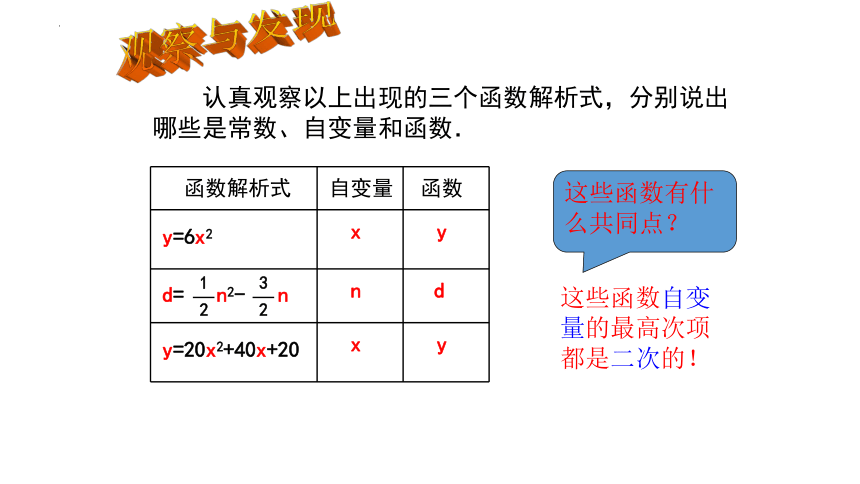
观察与发现
认真观察以上出现的三个函数解析式,分别说出哪些是常数、自变量和函数.
这些函数有什么共同点?
这些函数自变量的最高次项都是二次的!
定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)其中,x是自变量,ax2是二次项,a 是二次项系数;bx是一次项,b是一次项系数;c是常数项。
(2)等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。
注意:
2
做一做:
(1)正方形边长为x(cm),它的面积y(cm2)是多少?
(2)矩形的长是4厘米,宽是3厘米,如果将其长增加x厘米,宽增加2x厘米,则面积增加到y平方厘米,试写出y与x的关系式.
1.下列函数中,哪些是二次函数
抓住机遇 展示自我
是
不是
是
不是
先化简后判断
2、下列函数中,哪些是二次函数?
( )
( )
( )
否
是
否
否
( )
是
( )
知识运用
3、下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x-2+x (6)y=x2-x(1+x)
例1: 关于x的函数 是二次函数, 求m的值.
解: 由题意可得
注意:二次函数的二次项系数不能为零
驶向胜利的彼岸
练习1、m取何值时,函数是y= (m+1)x
+(m-3)x+m 是二次函数?
知识运用
1 .下列函数中,(x是自变量),是二次函数的为( )
A. y=ax2+bx+c B. y2=x2-4x+1
C. y=x2 D. y=22+ x+1
2. 函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A. m,n是常数,且m≠0 B. m,n是常数,且n≠0
C. m,n是常数,且m≠n D. m,n为任何实数
★巩固检测★
多边形的对角线总条数d与边数n有什么关系?
如果多边形有n条边,那么它有 个顶点,从一个顶点出发,可以作 条对角线.
M
N
3.
课堂小结
问题导入,列关系式
探索二次关系式共同点
归纳二次函数概念
二次函数y=ax +bx+c
(a,b,c为常数,a≠0)
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
确定二次函数解析式及自变量的取值范围
22.1.1 二次函数
基础回顾 什么叫函数
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。x叫自变量,y叫x的函数。 。
目前,我们已经学习了那几种类型的函数?
二次函数
变量之间的关系
函数
一次函数
y=kx+b (k≠0)
正比例函数y=kx (k≠0)
基础回顾
观察篮球运动轨迹
讨论与思考:
1、正方形的六个面是全等的正方形,设正方体的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,他们的具体关系是可以表示为什么?
2、多边形的对角线数d与边数n有什么关系?
y=6x2
d= n(n-3)
1
2
d= n2- n
1
2
3
2
即
x
3、某工厂一种产品现在的年产量是20件,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
y=20(1+x)2
y=20x2+40x+20
即
y=6x2
d= n2- n
1
2
3
2
y=20x2+40x+20
自变量
函数
函数解析式
y
y
d
x
x
n
观察与发现
认真观察以上出现的三个函数解析式,分别说出哪些是常数、自变量和函数.
这些函数有什么共同点?
这些函数自变量的最高次项都是二次的!
定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠ 0)的函数叫做x的二次函数。
(1)其中,x是自变量,ax2是二次项,a 是二次项系数;bx是一次项,b是一次项系数;c是常数项。
(2)等式的右边最高次数为 ,可以没有一次项和常数项,但不能没有二次项。
注意:
2
做一做:
(1)正方形边长为x(cm),它的面积y(cm2)是多少?
(2)矩形的长是4厘米,宽是3厘米,如果将其长增加x厘米,宽增加2x厘米,则面积增加到y平方厘米,试写出y与x的关系式.
1.下列函数中,哪些是二次函数
抓住机遇 展示自我
是
不是
是
不是
先化简后判断
2、下列函数中,哪些是二次函数?
( )
( )
( )
否
是
否
否
( )
是
( )
知识运用
3、下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x-2+x (6)y=x2-x(1+x)
例1: 关于x的函数 是二次函数, 求m的值.
解: 由题意可得
注意:二次函数的二次项系数不能为零
驶向胜利的彼岸
练习1、m取何值时,函数是y= (m+1)x
+(m-3)x+m 是二次函数?
知识运用
1 .下列函数中,(x是自变量),是二次函数的为( )
A. y=ax2+bx+c B. y2=x2-4x+1
C. y=x2 D. y=22+ x+1
2. 函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )
A. m,n是常数,且m≠0 B. m,n是常数,且n≠0
C. m,n是常数,且m≠n D. m,n为任何实数
★巩固检测★
多边形的对角线总条数d与边数n有什么关系?
如果多边形有n条边,那么它有 个顶点,从一个顶点出发,可以作 条对角线.
M
N
3.
课堂小结
问题导入,列关系式
探索二次关系式共同点
归纳二次函数概念
二次函数y=ax +bx+c
(a,b,c为常数,a≠0)
二次函数的判别:
①含未知数的代数式为整式;
②未知数最高次数为2;
③二次项系数不为0.
确定二次函数解析式及自变量的取值范围
同课章节目录
