2022-2023学年人教版八年级数学上册14.1.2 幂的乘方 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册14.1.2 幂的乘方 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
14.1.2 幂的乘方
回顾:1.同底数幂乘法的运算性质是什么
2.什么是乘方 43表示什么意思
43表示3个4相乘,即43 =4×4×4.
同底数的幂相乘,底数不变,指数相加.
(m,n都是正整数)
试一试:
幂的乘方
引例:已知一个正方形的边长为8,则它的面积是多少
2 2 2
2 3
3 3 3 3
3 4
做一做:
根据乘方的意义及同底数幂乘法的运算性质填空:
议一议:1.试说出每个运算步骤的根据;
2.观察算式中底数、指数的关系,你发现有何规律
3.根据填空题的规律,请猜想
3×2
你能证明你的猜想吗
幂的乘方
幂的乘方,底数不变,指数相乘.
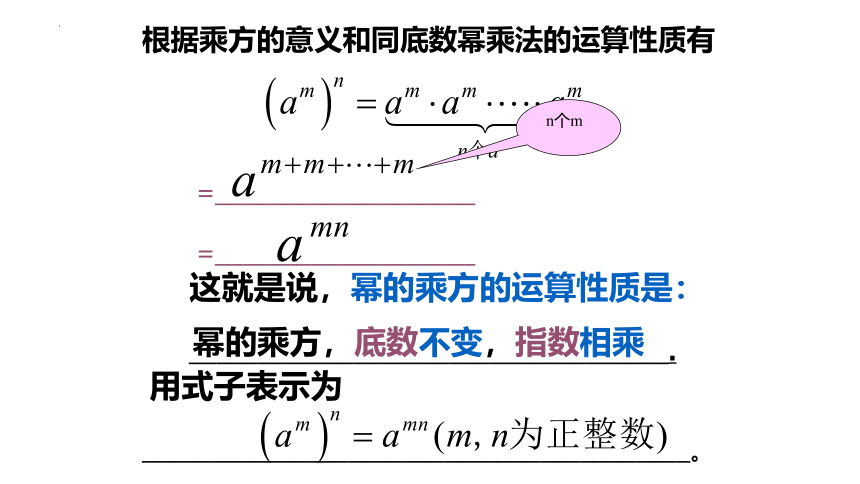
根据乘方的意义和同底数幂乘法的运算性质有
=___________________
=___________________
这就是说,幂的乘方的运算性质是:
___________________________________.
用式子表示为
________________________________________。
n个m
幂的乘方,底数不变,指数相乘
例题:计算
解:
巩固练习 1.请你模仿例题出一道关于幂的乘方的运算的题,考一考你同组的同学.
(am)n
=am . am ..... am
=am+m+...+m
=amn
(根据 )
(根据 ).
同底数幂的乘法法则
乘方的意义
n个am
n个m
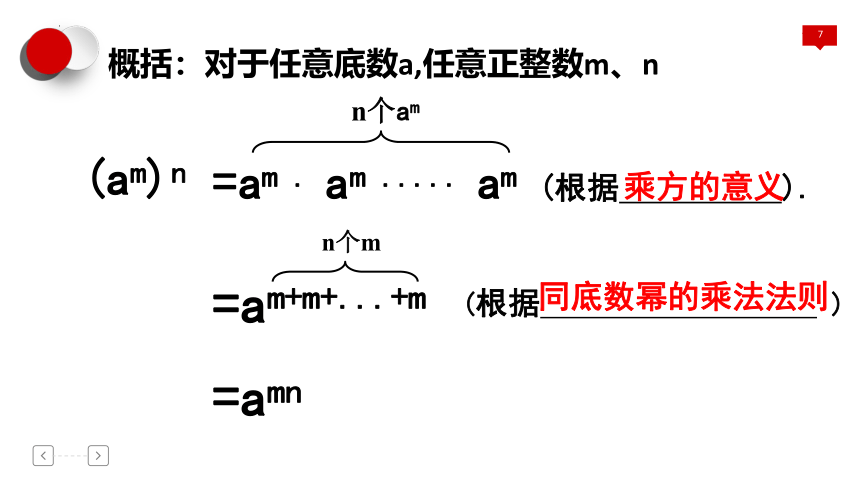
概括:对于任意底数a,任意正整数m、n
即幂的乘方, 底数不变,指数相乘。
(m、n都是正整数)
以后直接利用它进行计算。
幂的乘方运算法则
三、实战操作
例1、计算:
先算幂的乘方,再算同底数幂的乘法
底数a,可以是单项式,也可以是多项式
例2、下面计算是否正确?如有错误请改正。
(1)X3·X3=2X3
(2) (a3)7=a10
(3) (X5)3=X15
(4)-(a3)4=a12
√
×
×
×
X3·X3=X6
(a3)7=a21
-(a3)4=-a12
同底数幂的乘法 幂的乘方
法则
字母表示
底数不变
指数相加
底数不变
指数相乘
am.an=amn
(m、n为正整数)
(am)n=amn
(m、n为正整数)
变式训练
amn
=(am)n
=(an)m
(m、n都是正整数)
公式逆用
幂的乘方运算法则
(am)n=amn (m、n为正整数)
即幂的乘方, 底数不变,指数相乘。
推广公式
amn
=(am)n
=(an)m
(m、n都是正整数)
公式逆用
四、小结
当堂检测
1.计算下列各题:
(1) (52)3 (2) -(m3)4
(3) (63)m (4) a3·a5+(a2)4
=56
=-m12
=63m
=2a8
当堂检测
2.已知am=2,求a3m的值。
解:
∴a3m=(am)3=23=8
∵am=2
作业布置
1、选择题:下列各式计算正确的是( )
A. 3a2-a2=2 B. (a2)3·a4=a24
C. (a2)3·a+a7=2a7 D. - (a2)4=a8
2、计算题:
(1) (75)2 (2) (-4n)5
(3) (a3)m (4) (a3)4·a2
3、若a2n=3,求(a3n)4的值. (选做)
14.1.2 幂的乘方
回顾:1.同底数幂乘法的运算性质是什么
2.什么是乘方 43表示什么意思
43表示3个4相乘,即43 =4×4×4.
同底数的幂相乘,底数不变,指数相加.
(m,n都是正整数)
试一试:
幂的乘方
引例:已知一个正方形的边长为8,则它的面积是多少
2 2 2
2 3
3 3 3 3
3 4
做一做:
根据乘方的意义及同底数幂乘法的运算性质填空:
议一议:1.试说出每个运算步骤的根据;
2.观察算式中底数、指数的关系,你发现有何规律
3.根据填空题的规律,请猜想
3×2
你能证明你的猜想吗
幂的乘方
幂的乘方,底数不变,指数相乘.
根据乘方的意义和同底数幂乘法的运算性质有
=___________________
=___________________
这就是说,幂的乘方的运算性质是:
___________________________________.
用式子表示为
________________________________________。
n个m
幂的乘方,底数不变,指数相乘
例题:计算
解:
巩固练习 1.请你模仿例题出一道关于幂的乘方的运算的题,考一考你同组的同学.
(am)n
=am . am ..... am
=am+m+...+m
=amn
(根据 )
(根据 ).
同底数幂的乘法法则
乘方的意义
n个am
n个m
概括:对于任意底数a,任意正整数m、n
即幂的乘方, 底数不变,指数相乘。
(m、n都是正整数)
以后直接利用它进行计算。
幂的乘方运算法则
三、实战操作
例1、计算:
先算幂的乘方,再算同底数幂的乘法
底数a,可以是单项式,也可以是多项式
例2、下面计算是否正确?如有错误请改正。
(1)X3·X3=2X3
(2) (a3)7=a10
(3) (X5)3=X15
(4)-(a3)4=a12
√
×
×
×
X3·X3=X6
(a3)7=a21
-(a3)4=-a12
同底数幂的乘法 幂的乘方
法则
字母表示
底数不变
指数相加
底数不变
指数相乘
am.an=amn
(m、n为正整数)
(am)n=amn
(m、n为正整数)
变式训练
amn
=(am)n
=(an)m
(m、n都是正整数)
公式逆用
幂的乘方运算法则
(am)n=amn (m、n为正整数)
即幂的乘方, 底数不变,指数相乘。
推广公式
amn
=(am)n
=(an)m
(m、n都是正整数)
公式逆用
四、小结
当堂检测
1.计算下列各题:
(1) (52)3 (2) -(m3)4
(3) (63)m (4) a3·a5+(a2)4
=56
=-m12
=63m
=2a8
当堂检测
2.已知am=2,求a3m的值。
解:
∴a3m=(am)3=23=8
∵am=2
作业布置
1、选择题:下列各式计算正确的是( )
A. 3a2-a2=2 B. (a2)3·a4=a24
C. (a2)3·a+a7=2a7 D. - (a2)4=a8
2、计算题:
(1) (75)2 (2) (-4n)5
(3) (a3)m (4) (a3)4·a2
3、若a2n=3,求(a3n)4的值. (选做)
