2022—2023学年人教版数学九年级上册21.2.4 一元二次方程的根与系数的关系 课件 (共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册21.2.4 一元二次方程的根与系数的关系 课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 10:37:36 | ||
图片预览






文档简介
(共15张PPT)
21.2.4 一元二次方程的根与系数的关系
1、一元二次方程的一般形式?
2、一元二次方程有实数根的条件是什么?
3、当△>0,△=0,△<0 根的情况如何?
4、一元二次方程的求根公式是什么?
复习回顾
A、好奇葩的数字,不好解
B、3秒钟?用计算器都来不及
新课引入
已知:如果一元二次方程
的两个根分别是 、 .
求证:
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理.
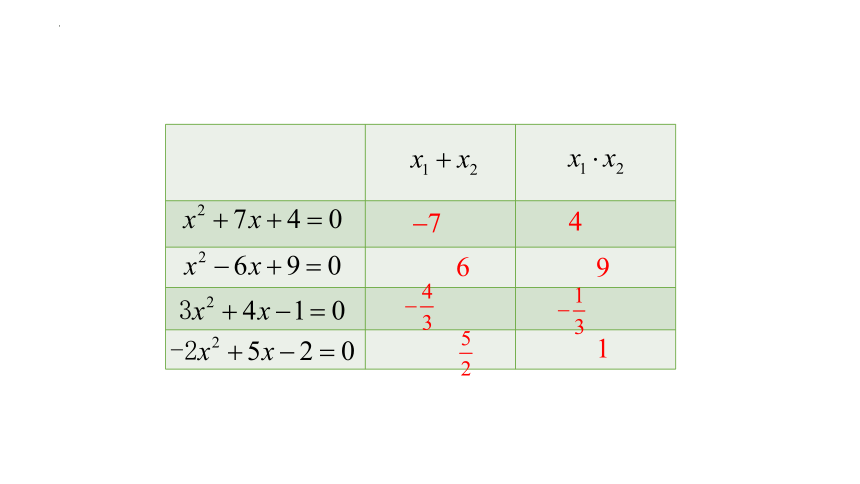
1、下列方程中,两根的和与两根
的积各是多少?
1、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和
变式(1)、求
(2)、求
(3)、求
2、已知方程 的两个实数根
是 且 ,求k的值。
1. 已知一元二次方程2x2+mx+3=0的一个根是1,则另一个根是______
练
练
一
解:
设方程的两个根分别是x1 , x2 ,其中x1=1 .
根据x1 . x2 = ,
即1. x2
∴ x2
练
练
一
2. 设x1,x2为方程x2-2x-1=0的两个根,求下列各式的值:
(1)x1+x2 = , (2) x1 x2 = ,
(3) = , (4) = .
a = 1 , b = -2 , c = -1.
解:
∴ x1+x2=
=2 ,
∴ x12 + x22 = (x1 + x2)2 - 2x1 x2
∵ (x1 + x2)2 =x12 + 2x1 x2 + x22
x1 x2=
=-1.
=-2 .
2
-1
-2
6
= 22 - 2×(-1)= 6
通过本节课你学到了什么?
一元二次方程的根与系数的关系:
如果一元二次方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,
那么x1+x2= , x1 x2=
(韦达定理)
常数项
一次项系数
二次项系数
注意系数符号。
归纳小结
21.2.4 一元二次方程的根与系数的关系
1、一元二次方程的一般形式?
2、一元二次方程有实数根的条件是什么?
3、当△>0,△=0,△<0 根的情况如何?
4、一元二次方程的求根公式是什么?
复习回顾
A、好奇葩的数字,不好解
B、3秒钟?用计算器都来不及
新课引入
已知:如果一元二次方程
的两个根分别是 、 .
求证:
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理.
1、下列方程中,两根的和与两根
的积各是多少?
1、利用根与系数的关系,求一元二次方程
两个根的;(1)平方和;(2)倒数和
变式(1)、求
(2)、求
(3)、求
2、已知方程 的两个实数根
是 且 ,求k的值。
1. 已知一元二次方程2x2+mx+3=0的一个根是1,则另一个根是______
练
练
一
解:
设方程的两个根分别是x1 , x2 ,其中x1=1 .
根据x1 . x2 = ,
即1. x2
∴ x2
练
练
一
2. 设x1,x2为方程x2-2x-1=0的两个根,求下列各式的值:
(1)x1+x2 = , (2) x1 x2 = ,
(3) = , (4) = .
a = 1 , b = -2 , c = -1.
解:
∴ x1+x2=
=2 ,
∴ x12 + x22 = (x1 + x2)2 - 2x1 x2
∵ (x1 + x2)2 =x12 + 2x1 x2 + x22
x1 x2=
=-1.
=-2 .
2
-1
-2
6
= 22 - 2×(-1)= 6
通过本节课你学到了什么?
一元二次方程的根与系数的关系:
如果一元二次方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,
那么x1+x2= , x1 x2=
(韦达定理)
常数项
一次项系数
二次项系数
注意系数符号。
归纳小结
同课章节目录
