2022-2023学年人教版九年级数学上册21.3 实际问题与一元二次方程 课件 (共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册21.3 实际问题与一元二次方程 课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 10:39:42 | ||
图片预览






文档简介
(共16张PPT)
21.3 实际问题与一元二次方程
问题1:列方程解应用题的基本步骤有哪些?
问题2:有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
本节课我们学习一元二次方程的应用.
审、设、列、解、验、答
环节一:复习展标
(一)复习引入
知识点
列一元二次方程解决实际问题
有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
你能解决这个问题吗?
环节二:自主学习
(三)自学互学
设每轮传染中平均一个人传染了x个人.
第一轮传染后有 人患了流感.
第二轮传染中的传染源为 人,第二轮传染后
有 人患了流感.
根据等量关系 “ ”列出方程 .
x+1
x+1
x+1+x(x+1)
两轮传染后,有121人患了流感
x+1+x(x+1)=121
解方程 x+1+x(x+1)=121
化简得:x2+2x-120=0
(x-10)(x+12)=0
x1=10, x2=-12(舍)
有更简单的方法解这个方程吗?
解方程 x+1+x(x+1)=121
提取公因式:(x+1)(x+1)=121
(x+1)2=121
x+1=±11
x1=10, x2=-12(舍)
(四)达标展示
思考:如果按这样的传染速度,三轮传染后有多少人患了流感?n轮后呢?
经过三轮传染后共有121×10+121=1331(人)患流感.
n轮后患流感的人数为(1+10)n=11n.
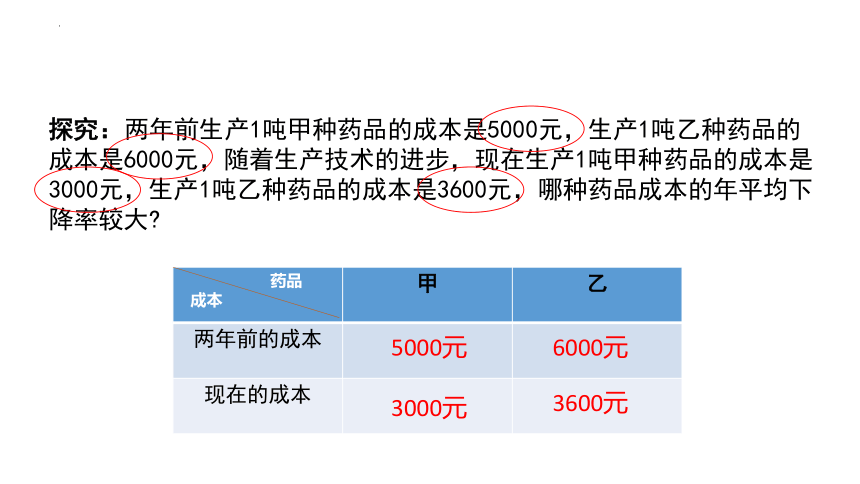
探究:两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大
药品 成本 甲 乙
两年前的成本
现在的成本
5000元
6000元
3000元
3600元
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率
1000元
1200元
?
?
本年成本=前一年成本-前一年成本×年下降率
=前一年成本×(1-年下降率)
=变化后的数量
变化前的数量×(1-年下降率)2
连续两年下降:
解:设甲种药品成本的年平均下降率为x
一年前甲种药品的成本为
5000-5000x=5000(1-x) 元,
现在甲种药品的成本为
=5000(1-x)2 元
5000(1-x)
(1-x)
解:设甲种药品成本的年平均下降率为x
由题意得
5000(1-x)2=3000
解方程,得
(1-x)2=0.6
年平均下降率应为小于1的正数
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率 22.5%.
1000元
1200元
?
解:设乙种药品成本的年平均下降率为y
由题意得 6000(1-y)2=3600
解方程,得
根据问题的实际意义
乙种药品成本的年平均下降率约为22.5%.
y1≈0.225,y2≈1.775
.
(27-3x +3)m
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长)中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则设与已有墙垂直的一-边为xm,则与已有墙平行的一边为
挑战自我
中考链接
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
某学校计划利用一片空地建一 个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米
(1)为了方便学生出行,学校决定在与墙平行的一面开一个 2米宽的门,那么这个车棚的长和宽分别应为多少米
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米
挑战自我
21.3 实际问题与一元二次方程
问题1:列方程解应用题的基本步骤有哪些?
问题2:有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
本节课我们学习一元二次方程的应用.
审、设、列、解、验、答
环节一:复习展标
(一)复习引入
知识点
列一元二次方程解决实际问题
有一人患了流感,经过两轮传染后共有121个人患了流感,每轮传染中平均一个人传染了几个人?
你能解决这个问题吗?
环节二:自主学习
(三)自学互学
设每轮传染中平均一个人传染了x个人.
第一轮传染后有 人患了流感.
第二轮传染中的传染源为 人,第二轮传染后
有 人患了流感.
根据等量关系 “ ”列出方程 .
x+1
x+1
x+1+x(x+1)
两轮传染后,有121人患了流感
x+1+x(x+1)=121
解方程 x+1+x(x+1)=121
化简得:x2+2x-120=0
(x-10)(x+12)=0
x1=10, x2=-12(舍)
有更简单的方法解这个方程吗?
解方程 x+1+x(x+1)=121
提取公因式:(x+1)(x+1)=121
(x+1)2=121
x+1=±11
x1=10, x2=-12(舍)
(四)达标展示
思考:如果按这样的传染速度,三轮传染后有多少人患了流感?n轮后呢?
经过三轮传染后共有121×10+121=1331(人)患流感.
n轮后患流感的人数为(1+10)n=11n.
探究:两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大
药品 成本 甲 乙
两年前的成本
现在的成本
5000元
6000元
3000元
3600元
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率
1000元
1200元
?
?
本年成本=前一年成本-前一年成本×年下降率
=前一年成本×(1-年下降率)
=变化后的数量
变化前的数量×(1-年下降率)2
连续两年下降:
解:设甲种药品成本的年平均下降率为x
一年前甲种药品的成本为
5000-5000x=5000(1-x) 元,
现在甲种药品的成本为
=5000(1-x)2 元
5000(1-x)
(1-x)
解:设甲种药品成本的年平均下降率为x
由题意得
5000(1-x)2=3000
解方程,得
(1-x)2=0.6
年平均下降率应为小于1的正数
根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
药品 成本 甲 乙
两年前的成本 5000元 6000元
现在的成本 3000元 3600元
年平均下降额
年平均下降率 22.5%.
1000元
1200元
?
解:设乙种药品成本的年平均下降率为y
由题意得 6000(1-y)2=3600
解方程,得
根据问题的实际意义
乙种药品成本的年平均下降率约为22.5%.
y1≈0.225,y2≈1.775
.
(27-3x +3)m
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长)中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则设与已有墙垂直的一-边为xm,则与已有墙平行的一边为
挑战自我
中考链接
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
某学校计划利用一片空地建一 个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米
(1)为了方便学生出行,学校决定在与墙平行的一面开一个 2米宽的门,那么这个车棚的长和宽分别应为多少米
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米
挑战自我
同课章节目录
