2022-2023学年人教版数学八年级上册 14.2.2 完全平方公式 课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册 14.2.2 完全平方公式 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 10:45:55 | ||
图片预览



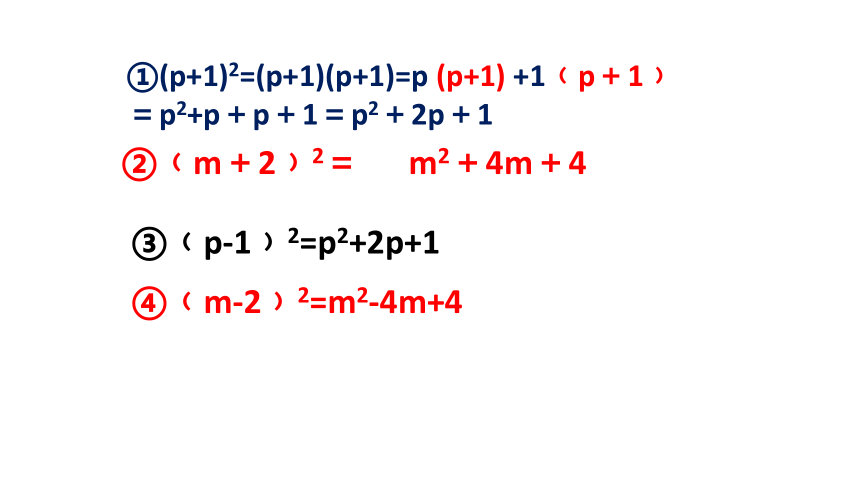

文档简介
(共16张PPT)
14.2.2 完全平方公式
(a+b)(a-b) = a2-b2
.
*平方差公式
判断*(2x+3)(3x-2)=6x2-6
2x(3x-2)+3(3x-2)=6x2-4x+9x-6=6x2-5x-6
一、复习引入
(× )
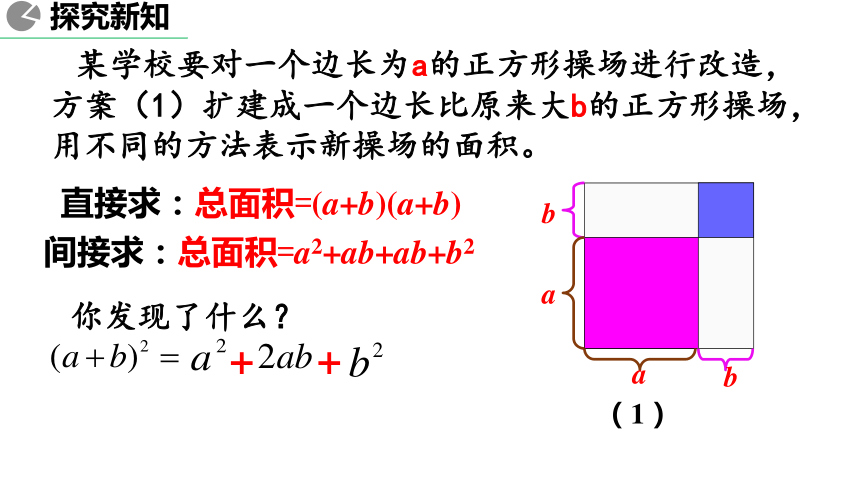
某学校要对一个边长为a的正方形操场进行改造,方案(1)扩建成一个边长比原来大b的正方形操场,用不同的方法表示新操场的面积。
b
a
b
a
(1)
+
+
探究新知
间接求:总面积=a2+ab+ab+b2
你发现了什么?
直接求:总面积=(a+b)(a+b)
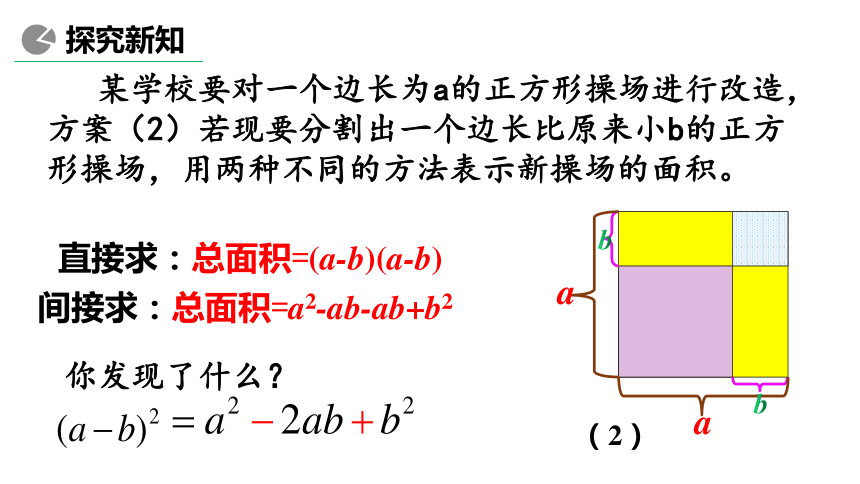
某学校要对一个边长为a的正方形操场进行改造,方案(2)若现要分割出一个边长比原来小b的正方形操场,用两种不同的方法表示新操场的面积。
b
a
b
a
(2)
探究新知
间接求:总面积=a2-ab-ab+b2
你发现了什么?
直接求:总面积=(a-b)(a-b)
二、探求新知
像研究平方差公式一样,我们探究一下(a+b)2的运算结果有什么规律.
计算下列各式,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1)=_______;
(2)(m+2)2=_______;
(3)(p-1)2=(p-1)(p-1)=________;
(4)(m-2)2=________;
①(p+1)2=(p+1)(p+1)=p (p+1) +1﹙p+1﹚=p2+p+p+1=p2+2p+1
②﹙m+2﹚2= m2+4m+4
③﹙p-1﹚2=p2+2p+1
④﹙m-2﹚2=m2-4m+4
计算下列各式,你能发现什么?
(p+1)2 =
(m+2)2=
(p-1)2 =
(m-2)2 =
p2+2p+1=p2+2×p×1+12
m2+4m+4=m2+2×m×2+22
p2-2p+1=p2-2×p×1+12
m2- 4m+4=m2-2×m×2+22
猜想 (a+b)2=
(a -b)2=
a2+2ab+b2
a2 - 2ab+b2
认识 完全平方 公式
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
结构特征:
用自己的语言叙述上面的公式
语言表述:
两数和 的平方
等于
这两数的平方和
加上 这两数乘积的两倍.
(差)
(减去)
例 运用完全平方公式计算:
(1)(4m+n)2; (2)(y- )2.
例 运用完全平方公式计算:
(1)1022; (2)992.
解:(1)1022
=(100+2)2
=1002+22+2×100×2
=10404;
(2)992
=(100-1)2
=1002+12-2×100×1
=9801.
思考
(1) 与 相等吗?
(2) 与 相等吗?
(3) 与 相等吗?为什么?
(1)(2)相等.因为互为相反数的数或式子平方相等.(3)不相等.因为前者是完全平方,后者是平方差.
1.若(x-5)2=x2+kx+25,则k= ;
2.若4x2+mx+9是完全平方式,则m= .
-10
解析:(1)∵(x-5)2=x2-10x+25=x2+kx+25,
∴k=-10.
(2)∵4x2+mx+9是完全平方式,
∴4x2+mx+9=(2x±3)2,∴m=±12.
±12
口诀:首平方,尾平方,
积的2倍放中央,
s式子 首 尾
表示
(1) (p+q)2=p2+q2
(2) (a+2b)2=a2+4ab+2b2
(3) (a2+1)2=a4+2a+1
(4) (-s+t)2=s2-2st+t2
判断题
+2pq+q2
4
a2
( × )
( × )
( × )
( √ )
课堂练习
课堂小结
(a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
口诀:首平方,尾平方,积的2倍放中央
14.2.2 完全平方公式
(a+b)(a-b) = a2-b2
.
*平方差公式
判断*(2x+3)(3x-2)=6x2-6
2x(3x-2)+3(3x-2)=6x2-4x+9x-6=6x2-5x-6
一、复习引入
(× )
某学校要对一个边长为a的正方形操场进行改造,方案(1)扩建成一个边长比原来大b的正方形操场,用不同的方法表示新操场的面积。
b
a
b
a
(1)
+
+
探究新知
间接求:总面积=a2+ab+ab+b2
你发现了什么?
直接求:总面积=(a+b)(a+b)
某学校要对一个边长为a的正方形操场进行改造,方案(2)若现要分割出一个边长比原来小b的正方形操场,用两种不同的方法表示新操场的面积。
b
a
b
a
(2)
探究新知
间接求:总面积=a2-ab-ab+b2
你发现了什么?
直接求:总面积=(a-b)(a-b)
二、探求新知
像研究平方差公式一样,我们探究一下(a+b)2的运算结果有什么规律.
计算下列各式,你能发现什么规律?
(1)(p+1)2=(p+1)(p+1)=_______;
(2)(m+2)2=_______;
(3)(p-1)2=(p-1)(p-1)=________;
(4)(m-2)2=________;
①(p+1)2=(p+1)(p+1)=p (p+1) +1﹙p+1﹚=p2+p+p+1=p2+2p+1
②﹙m+2﹚2= m2+4m+4
③﹙p-1﹚2=p2+2p+1
④﹙m-2﹚2=m2-4m+4
计算下列各式,你能发现什么?
(p+1)2 =
(m+2)2=
(p-1)2 =
(m-2)2 =
p2+2p+1=p2+2×p×1+12
m2+4m+4=m2+2×m×2+22
p2-2p+1=p2-2×p×1+12
m2- 4m+4=m2-2×m×2+22
猜想 (a+b)2=
(a -b)2=
a2+2ab+b2
a2 - 2ab+b2
认识 完全平方 公式
(a+b)2 = a2+2ab+b2 .
(a b)2 = a2 2ab+b2 .
结构特征:
用自己的语言叙述上面的公式
语言表述:
两数和 的平方
等于
这两数的平方和
加上 这两数乘积的两倍.
(差)
(减去)
例 运用完全平方公式计算:
(1)(4m+n)2; (2)(y- )2.
例 运用完全平方公式计算:
(1)1022; (2)992.
解:(1)1022
=(100+2)2
=1002+22+2×100×2
=10404;
(2)992
=(100-1)2
=1002+12-2×100×1
=9801.
思考
(1) 与 相等吗?
(2) 与 相等吗?
(3) 与 相等吗?为什么?
(1)(2)相等.因为互为相反数的数或式子平方相等.(3)不相等.因为前者是完全平方,后者是平方差.
1.若(x-5)2=x2+kx+25,则k= ;
2.若4x2+mx+9是完全平方式,则m= .
-10
解析:(1)∵(x-5)2=x2-10x+25=x2+kx+25,
∴k=-10.
(2)∵4x2+mx+9是完全平方式,
∴4x2+mx+9=(2x±3)2,∴m=±12.
±12
口诀:首平方,尾平方,
积的2倍放中央,
s式子 首 尾
表示
(1) (p+q)2=p2+q2
(2) (a+2b)2=a2+4ab+2b2
(3) (a2+1)2=a4+2a+1
(4) (-s+t)2=s2-2st+t2
判断题
+2pq+q2
4
a2
( × )
( × )
( × )
( √ )
课堂练习
课堂小结
(a+b)2=a2+2ab+b2,
(a-b) 2 = a2-2ab +b2.
口诀:首平方,尾平方,积的2倍放中央
