2022-2023学年人教版八年级数学上册14.3.1 提公因式法 课件 (共16张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册14.3.1 提公因式法 课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 10:44:11 | ||
图片预览





文档简介
(共16张PPT)
14.3.1 提公因式法
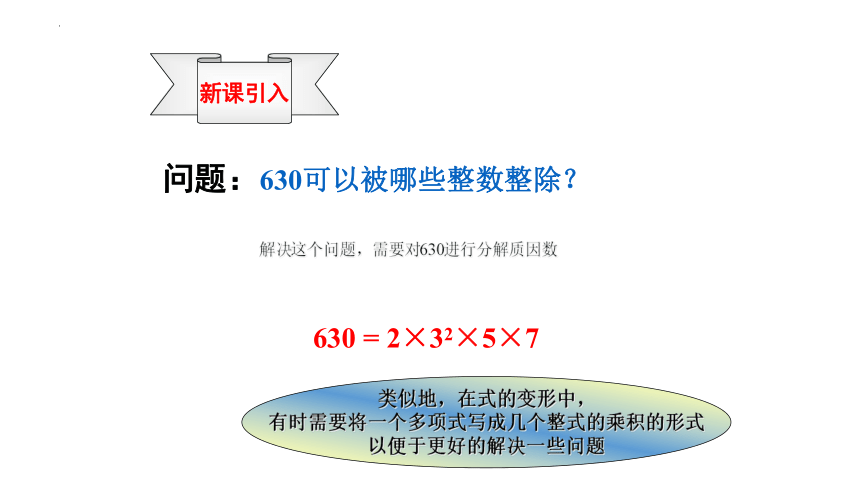
问题:630可以被哪些整数整除?
解决这个问题,需要对630进行分解质因数
630 = 2×32×5×7
类似地,在式的变形中,
有时需要将一个多项式写成几个整式的乘积的形式
以便于更好的解决一些问题
新课引入
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=_ __
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
3x(x-1)= __,
m(a+b+c )= _
(m+4)(m-4)= _ _
(x-3)2= ,
a(a+1)(a-1)= _ _,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
想一想
由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
答:由a(a+1)(a-1)得到a3-a的变形
是整式乘法,由a3-a得到a(a+1)(a-1)
的变形与上面的变形互为逆过程.
上面我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式 ,也叫做把这个多项式 。
分解因式
因式分解
因式分解
整式乘法
因式分解与整式乘法是逆变形
想一想: 分解因式与整式乘法有何关系
a3-a=a(a+1)(a-1)
a(a+1)(a-1)
a3-a
温馨提示
判断是否是因式分解 要看等式的左边是否是一个多项式,右边是否是几个整式的积的形式。
试一试:
下列由左边到右边的变形中,哪些是因式分解,哪些不是?
(1) ( )
(2)(x+2)(x-2)= x2-4( )
(3)a2-b2+1=(a+b)(a-b)+1( )
(4)ax2+ay2=a(x2+y2) ( )
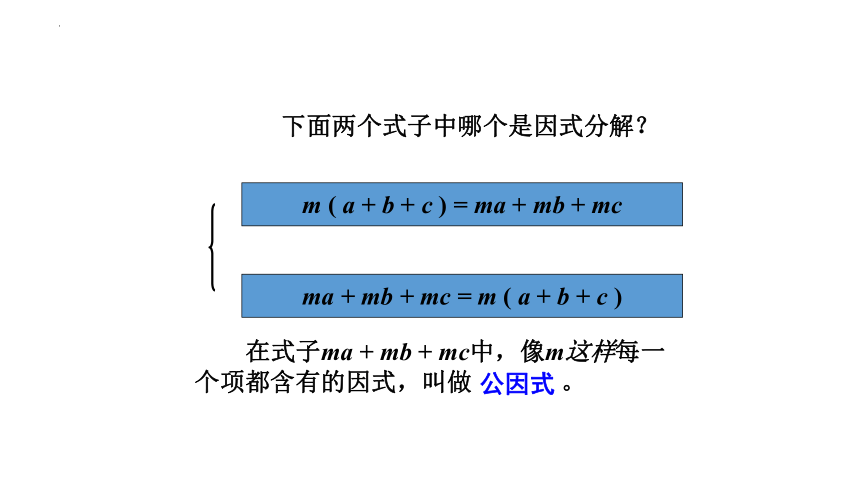
m ( a + b + c ) = ma + mb + mc
下面两个式子中哪个是因式分解?
在式子ma + mb + mc中,像m这样每一个项都含有的因式,叫做 。
公因式
ma + mb + mc = m ( a + b + c )
例: 找 3 x 2 – 6 x 的公因式。
系数:最大公约数
3
字母:相同字母
x
所以,公因式是
指数:最低次幂
1
3x
解:
3x2-6x
=3x·x-3x·2
=3x(x-2)
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
分析(1):由公因式的几个特征,我们可以这样确定公因式:
1、定系数:系数-5和25的最大公约数为5,故公因式的系数为5;
2、定字母:两项中的相同字母是a,故公因式的字母取a;
3、定指数:相同字母a的最小指数为1,故a的指数取为1; 所以,-5a2+25a的公因式为:5a
解(1): -5a2+25a
=5a (-a)+5a 5
=5a(-a+5) 把5a提到括号的外面
= -5a(a-5) 再把负号提到括号的外面
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
分析(2):对于3a2-9ab;
1、定系数:3和-9的最大公约数是3,故公因式的系数为 3;
2、定字母:观察可知相同字母是a, 故公因式的字母取为a;
3、定指数:相同字母a的最小指数为1,故a的指数取为1;
所以多项式3a2-9ab的公因式为:3a
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
解:3a2-9ab
=3a a-3a 3b
=3a(a-3b) 把3a提到括号的外面
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
做一做
1.把下列多项式因式分解
(1)3a+3b
(2)5x-5y+5z
(3) 4a3b-2a2b2
提公因式法因式分解
比较一下看,你做得怎么样?
解:(1)3a+3b
=3(a+b)
(2) 5x-5y+5z
=5(x-y+z)
(3) 4a3b-2a2b2
=2a2b(2a-b)
练一练
把下列各式因式分解
(4)
解:原式
解:原式
解:原式
解:原式
1.把下列各式因式分解
2.已知
求代数式 的值.
拓展提高
(1)
(2)
(1)
14.3.1 提公因式法
问题:630可以被哪些整数整除?
解决这个问题,需要对630进行分解质因数
630 = 2×32×5×7
类似地,在式的变形中,
有时需要将一个多项式写成几个整式的乘积的形式
以便于更好的解决一些问题
新课引入
根据左面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=_ __
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
计算下列各式:
3x(x-1)= __,
m(a+b+c )= _
(m+4)(m-4)= _ _
(x-3)2= ,
a(a+1)(a-1)= _ _,
3x2 - 3x
ma+mb+mc
m2 -16
x2-6x+9
a3-a
3x(x-1)
m(a+b+c)
(m+4)(m-4)
(x-3)2
a(a+1)(a-1)
想一想
由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
答:由a(a+1)(a-1)得到a3-a的变形
是整式乘法,由a3-a得到a(a+1)(a-1)
的变形与上面的变形互为逆过程.
上面我们把一个多项式化成了几个整式的积的形式,像这样的式子变形叫做把这个多项式 ,也叫做把这个多项式 。
分解因式
因式分解
因式分解
整式乘法
因式分解与整式乘法是逆变形
想一想: 分解因式与整式乘法有何关系
a3-a=a(a+1)(a-1)
a(a+1)(a-1)
a3-a
温馨提示
判断是否是因式分解 要看等式的左边是否是一个多项式,右边是否是几个整式的积的形式。
试一试:
下列由左边到右边的变形中,哪些是因式分解,哪些不是?
(1) ( )
(2)(x+2)(x-2)= x2-4( )
(3)a2-b2+1=(a+b)(a-b)+1( )
(4)ax2+ay2=a(x2+y2) ( )
m ( a + b + c ) = ma + mb + mc
下面两个式子中哪个是因式分解?
在式子ma + mb + mc中,像m这样每一个项都含有的因式,叫做 。
公因式
ma + mb + mc = m ( a + b + c )
例: 找 3 x 2 – 6 x 的公因式。
系数:最大公约数
3
字母:相同字母
x
所以,公因式是
指数:最低次幂
1
3x
解:
3x2-6x
=3x·x-3x·2
=3x(x-2)
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
分析(1):由公因式的几个特征,我们可以这样确定公因式:
1、定系数:系数-5和25的最大公约数为5,故公因式的系数为5;
2、定字母:两项中的相同字母是a,故公因式的字母取a;
3、定指数:相同字母a的最小指数为1,故a的指数取为1; 所以,-5a2+25a的公因式为:5a
解(1): -5a2+25a
=5a (-a)+5a 5
=5a(-a+5) 把5a提到括号的外面
= -5a(a-5) 再把负号提到括号的外面
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
分析(2):对于3a2-9ab;
1、定系数:3和-9的最大公约数是3,故公因式的系数为 3;
2、定字母:观察可知相同字母是a, 故公因式的字母取为a;
3、定指数:相同字母a的最小指数为1,故a的指数取为1;
所以多项式3a2-9ab的公因式为:3a
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
解:3a2-9ab
=3a a-3a 3b
=3a(a-3b) 把3a提到括号的外面
例1 把下列多项式分解因式:
(1)-5a2+25a(2)3a2-9ab
做一做
1.把下列多项式因式分解
(1)3a+3b
(2)5x-5y+5z
(3) 4a3b-2a2b2
提公因式法因式分解
比较一下看,你做得怎么样?
解:(1)3a+3b
=3(a+b)
(2) 5x-5y+5z
=5(x-y+z)
(3) 4a3b-2a2b2
=2a2b(2a-b)
练一练
把下列各式因式分解
(4)
解:原式
解:原式
解:原式
解:原式
1.把下列各式因式分解
2.已知
求代数式 的值.
拓展提高
(1)
(2)
(1)
