2022-2023学年人教版八年级数学上册15.3 分式方程 课件 (共14张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册15.3 分式方程 课件 (共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 10:47:25 | ||
图片预览



文档简介
(共14张PPT)
15.3 分式方程
延时符
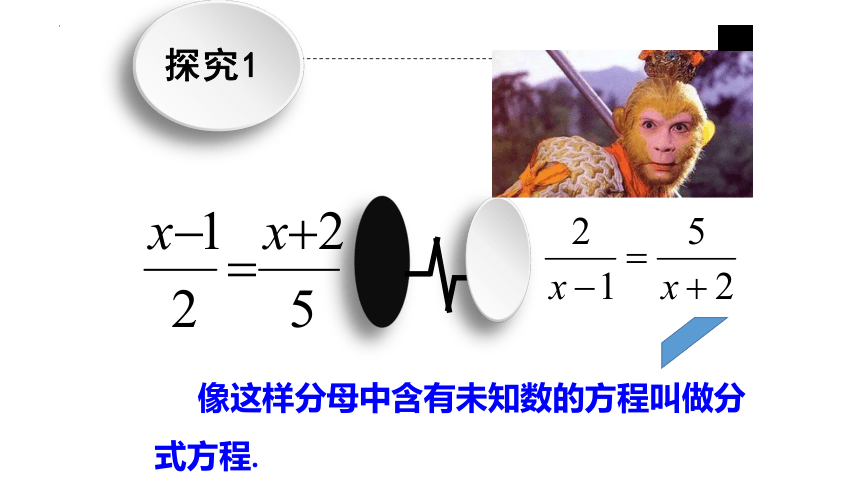
探究1
像这样分母中含有未知数的方程叫做分式方程.
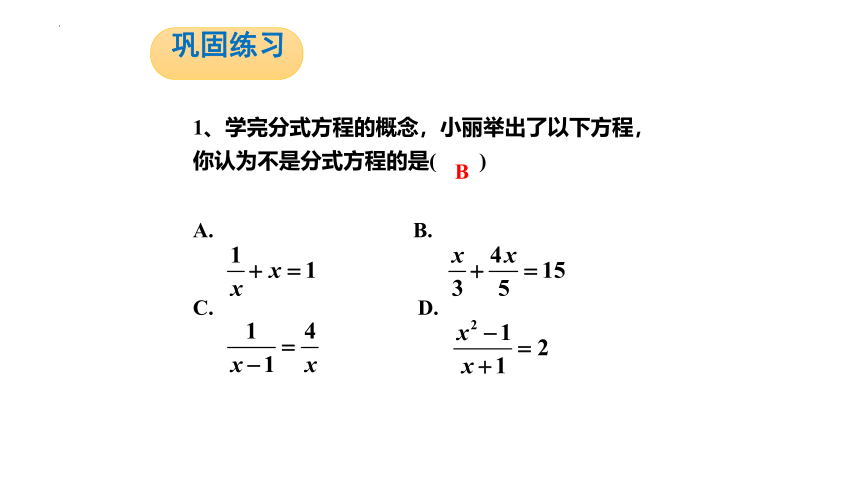
1、学完分式方程的概念,小丽举出了以下方程,你认为不是分式方程的是( )
B.
C. D.
B
巩固练习
1、学完分式方程的概念,小丽举出了以下方程,你认为不是分式方程的是( )
B.
C. D.
B
巩固练习
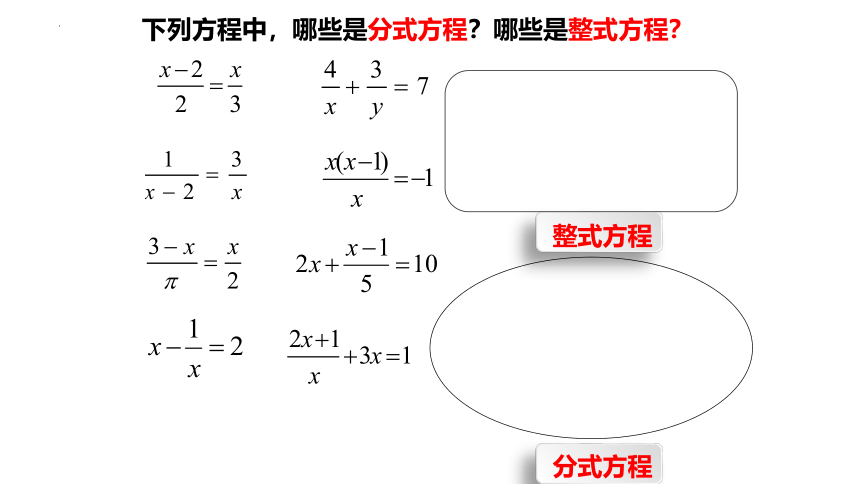
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
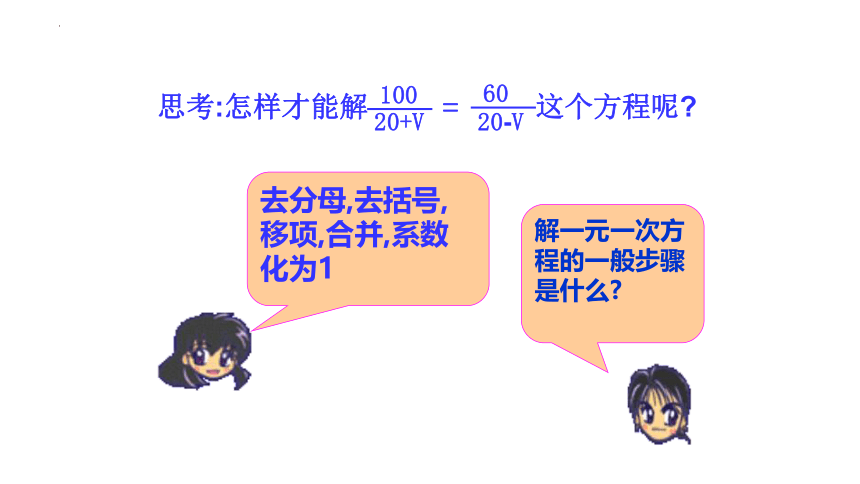
思考:怎样才能解 这个方程呢
100
20+V
60
20-V
=
去分母,去括号,移项,合并,系数化为1
解一元一次方程的一般步骤是什么
【解分式方程】
解分式方程
100
20+V
60
20-V
=
解:
在方程两边都乘以最简公分母(20+v)(20-v)得,
解这个整式方程,得v=5
100(20-v)=60(20+v)
检验:把v = 5 代入原方程中,左边=右边
因此v=5是原方程的解
分式方程
解分式分式方程的一般思路
整式方程
去分母
两边都乘以最简公分母
【解分式方程】
解分式方程
1
x-5
10
=
x2-25
解:
在方程两边都乘以最简公分母(x+5)(x-5)得,
解这个整式方程,得x=5
x+5=10
检验:把x = 5 代入原方程中,发现x-5和x2-25的值都为0,相应的分式无意义,因此x=5虽是方程x+5=10的解,但不是原分式方程
的解.实际上,这个分式方程无解.
1
x-5
10
=
x2-25
【分式方程的解】
思考
上面两个分式方程中,为什么
100
20+V
60
20-V
=
去分母后得到的整式方程的解就是它的解,而
去分母后得到的整式方程的解却不
1
x-5
10
=
x2-25
是原分式方程的解呢?
1
x-5
10
=
x2-25
我们来观察去分母的过程
100
20+V
60
20-V
=
100(20-v)=60(20+v)
x+5=10
两边同乘(20+v)(20-v)
当v=5时,(20+v)(20-v)≠0
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
【分式方程解的检验】
1
x-5
10
=
x2-25
100
20+V
60
20-V
=
100(20-v)=60(20+v)
x+5=10
两边同乘(20+v)(20-v)
当v=5时,(20+v)(20-v)≠0
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
解分式方程时,去分母后所得整式方程的解有可能
使原方程的分母为0,所以分式方程的解必须检验.
怎样检验这个整式方程的解是不是原分式的解?
解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程的思路是:
分式方程
整式方程
去分母
一化二解三检验
解分式方程 1.
解分式方程 2.
【小试牛刀】
解关于x的方程 产生增根,则常数m的值等于( )
(A)-2 (B)-1 (C ) 1 (D) 2
x-3
x-1
x-1
m
=
当m为何值时,方程 会产生增根?
补充练习:
根据你发现的规律
(1)写出第n个式子 ,
(2)利用规律计算:
(3)利用规律解方程:
※已知:
拓展与延伸:(选做)
布置作业
15.3 分式方程
延时符
探究1
像这样分母中含有未知数的方程叫做分式方程.
1、学完分式方程的概念,小丽举出了以下方程,你认为不是分式方程的是( )
B.
C. D.
B
巩固练习
1、学完分式方程的概念,小丽举出了以下方程,你认为不是分式方程的是( )
B.
C. D.
B
巩固练习
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
思考:怎样才能解 这个方程呢
100
20+V
60
20-V
=
去分母,去括号,移项,合并,系数化为1
解一元一次方程的一般步骤是什么
【解分式方程】
解分式方程
100
20+V
60
20-V
=
解:
在方程两边都乘以最简公分母(20+v)(20-v)得,
解这个整式方程,得v=5
100(20-v)=60(20+v)
检验:把v = 5 代入原方程中,左边=右边
因此v=5是原方程的解
分式方程
解分式分式方程的一般思路
整式方程
去分母
两边都乘以最简公分母
【解分式方程】
解分式方程
1
x-5
10
=
x2-25
解:
在方程两边都乘以最简公分母(x+5)(x-5)得,
解这个整式方程,得x=5
x+5=10
检验:把x = 5 代入原方程中,发现x-5和x2-25的值都为0,相应的分式无意义,因此x=5虽是方程x+5=10的解,但不是原分式方程
的解.实际上,这个分式方程无解.
1
x-5
10
=
x2-25
【分式方程的解】
思考
上面两个分式方程中,为什么
100
20+V
60
20-V
=
去分母后得到的整式方程的解就是它的解,而
去分母后得到的整式方程的解却不
1
x-5
10
=
x2-25
是原分式方程的解呢?
1
x-5
10
=
x2-25
我们来观察去分母的过程
100
20+V
60
20-V
=
100(20-v)=60(20+v)
x+5=10
两边同乘(20+v)(20-v)
当v=5时,(20+v)(20-v)≠0
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
【分式方程解的检验】
1
x-5
10
=
x2-25
100
20+V
60
20-V
=
100(20-v)=60(20+v)
x+5=10
两边同乘(20+v)(20-v)
当v=5时,(20+v)(20-v)≠0
两边同乘(x+5)(x-5)
当x=5时, (x+5)(x-5)=0
分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
解分式方程时,去分母后所得整式方程的解有可能
使原方程的分母为0,所以分式方程的解必须检验.
怎样检验这个整式方程的解是不是原分式的解?
解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程的思路是:
分式方程
整式方程
去分母
一化二解三检验
解分式方程 1.
解分式方程 2.
【小试牛刀】
解关于x的方程 产生增根,则常数m的值等于( )
(A)-2 (B)-1 (C ) 1 (D) 2
x-3
x-1
x-1
m
=
当m为何值时,方程 会产生增根?
补充练习:
根据你发现的规律
(1)写出第n个式子 ,
(2)利用规律计算:
(3)利用规律解方程:
※已知:
拓展与延伸:(选做)
布置作业
