2022—2023学年鲁教版(五四制)数学九年级上册 2.4 解直角三角形 同步练习 (Word版,含解析)
文档属性
| 名称 | 2022—2023学年鲁教版(五四制)数学九年级上册 2.4 解直角三角形 同步练习 (Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 11:47:39 | ||
图片预览




文档简介
第二章 直角三角形的边角关系
4 解直角三角形
基础过关
知识点1 解直角三角形
1.在Rt△ABC中,有下列情况,则直角三角形可解的是( )
A.已知BC=6,∠C=90° B.已知∠C=90°,∠A=60°,BC=5
C.已知∠C=90°,∠A=∠B D.已知∠C=∠B=45°
2.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AC=6, cosB=,则AD=___________.
3.如图,在Rt△ABC中,∠C=90°,BC=2,AC=2.解这个直角三角形.
4.在Rt△ABC中,a,b,c分别是∠A,∠B和 的对边,∠C=90°.根据下列条件解直角三角形(边长精确到0.1,角度精确到1°).
5.在△ABC中,已知∠C=90°,,∠A-∠B=30°,解这个直角三角形.
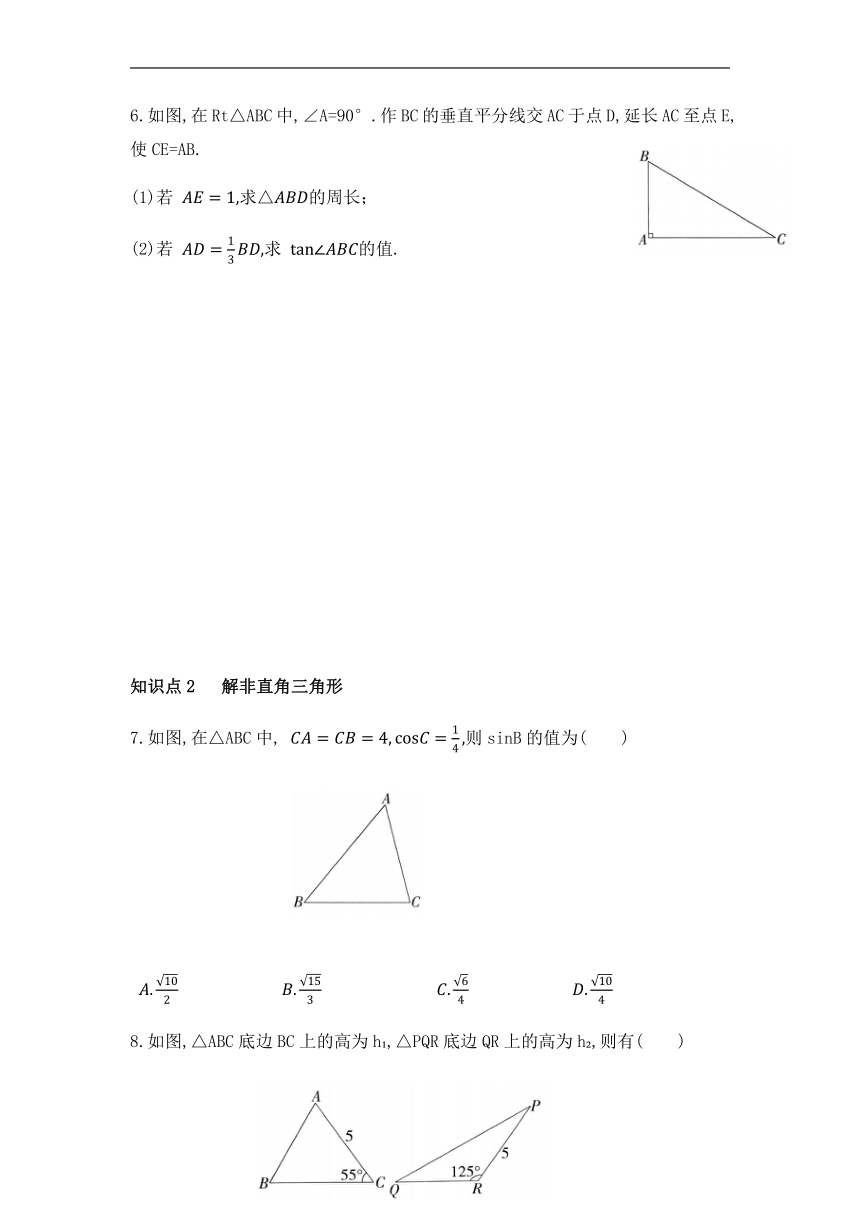
6.如图,在Rt△ABC中,∠A=90°.作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若 求△的周长;
(2)若 求 的值.
知识点2 解非直角三角形
7.如图,在△ABC中, 则sinB的值为( )
8.如图,△ABC底边BC上的高为h ,△PQR底边QR上的高为h ,则有( )
D.以上都有可能
9.如图,△ABC中,∠ABC=60°,∠ACB=45°,AC=2,则AB=____________.
10.如图,在平面直角坐标系中, 点A的坐标为(10,0).
(1)求点B的坐标;
(2)求sin∠OAB的值.
11.已知:如图,在△中,BC=AC,∠BCA=135°,求 的值.
12.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,BC.测得根据测得的数据,求AB的长(结果取整数).
参考数据:sin 58°≈0.85,cos58°≈0.53,tan58°≈1.60.
能力提升
13.如图,在△ABC中, 则AC的长为( )
14.如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 则tan∠DEC的值是_____________.
15.如图,在Rt△ABC中,∠C=90°,sinB=;D在BC边上,且∠ADC=45°,AC=5,求∠BAD的正切值.
16.[数学抽象]已知锐角△中,角A、B、C的对边分别为a、b、c,边角总满足关系式: .
(1)如图1,若 求b的值;
(2)某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD(如图2所示),若 米,AB=10米, 求景观桥CD的长度.
参考答案
基础过关
1.B 直角三角形中,已知直角的条件下,再知道一边一锐角,或两边,则直角三角形可解,四个选项中,只有B项的条件可解直角三角形,故选B.
2.答案
解析 在Rt△ABC中,
3.解析 在 中,
4.解析 (1)在Rt△ABC中,
(2)在 中,
(3)在Rt△ABC中,
(4)在Rt△ABC中,
(5)在 中,
∴
5.解析
6.解析 (1)根据题意作图,连接BD,则BD=CD.
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC.
∵AB=CE,∴△ABD的周长=AC+CE=AE=1.
故△ABD的周长为1.
∴设则
∵BD=CD,∴AC=AD+CD=4x.
在Rt△ABD中,
7.D 点A作ADLBC,垂足为D,如图所示.
在Rt△ACD中,CD=CA·cosC=∴ 在Rt△ABD中,
故选D.
8.A 如图,过点A作AD⊥BC于点D,则AD=h ,过点P作PE⊥QR交QR的延长线于点E,则PE=h ,
在Rt△ADC中, 在 中,h =PE=5×sin55°,∴h =h ,故选A.
9.答案 4
解析 如图,过点A作 垂足为D.
在 中,∵AC=
在中, 故填4.
10.解析 (1)如图,过点B作BC⊥OA于点C.
在Rt△BOC中,∠OCB=90°,OB=5,sin∠AOB=,∴,∴.
∴点B的坐标为(4,3).
(2)∵点A的坐标为(10,0),∴OA=10.∴AC=OA-OC=10-4=6.
11.解析 如图,过点B作BDLAC,交AC的延长线于点D,由题意得∠BCD=45°.
12.解析 如图,过点A作AD⊥BC,垂足为D.
∵∠ACB=45°,∴AD=CD.设
在Rt△ADB中,AD=AB·sin58°≈0.85xm,BD=AB·cos58°≈0.53x m.
∵BC=221m,即CD+BD=221m,∴0.85x+0.53x=221,∴x≈160.
答:AB的长约为160m.
能力提升
13.B 如图,过点A作AD⊥BC于D,则∠ADC=∠ADB=90°.
故选B.
14.答案
解析 如图,过点C作CF⊥BD于点F.
∵四边形ABCD是矩形,∴AB=CD,AB∥CD.∴∠ABE=∠CDF.
∵AE⊥BD,∴∠AEB=∠CFD=90°.∴△ABE≌△CDF(AAS).∴AE=CF,BE=FD.
∵AE⊥BD,,∴设,则.
故填
15.解析 如图,过点D作DE⊥AB于点E.
在 中,
在 中, ∠C=90°,∵ 即
根据勾股定理,得 ∴BD=BC-DC=12-5=7.
在Rt△BDE中,
在Rt△AED中,根据勾股定理,得AE=
16.解析 (1)∵∠B=45°,∠C=75°,∴∠A=60°.
即
(舍去).
∴CD的长度为8米.
4 解直角三角形
基础过关
知识点1 解直角三角形
1.在Rt△ABC中,有下列情况,则直角三角形可解的是( )
A.已知BC=6,∠C=90° B.已知∠C=90°,∠A=60°,BC=5
C.已知∠C=90°,∠A=∠B D.已知∠C=∠B=45°
2.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AC=6, cosB=,则AD=___________.
3.如图,在Rt△ABC中,∠C=90°,BC=2,AC=2.解这个直角三角形.
4.在Rt△ABC中,a,b,c分别是∠A,∠B和 的对边,∠C=90°.根据下列条件解直角三角形(边长精确到0.1,角度精确到1°).
5.在△ABC中,已知∠C=90°,,∠A-∠B=30°,解这个直角三角形.
6.如图,在Rt△ABC中,∠A=90°.作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若 求△的周长;
(2)若 求 的值.
知识点2 解非直角三角形
7.如图,在△ABC中, 则sinB的值为( )
8.如图,△ABC底边BC上的高为h ,△PQR底边QR上的高为h ,则有( )
D.以上都有可能
9.如图,△ABC中,∠ABC=60°,∠ACB=45°,AC=2,则AB=____________.
10.如图,在平面直角坐标系中, 点A的坐标为(10,0).
(1)求点B的坐标;
(2)求sin∠OAB的值.
11.已知:如图,在△中,BC=AC,∠BCA=135°,求 的值.
12.如图,A,B两点被池塘隔开,在AB外选一点C,连接AC,BC.测得根据测得的数据,求AB的长(结果取整数).
参考数据:sin 58°≈0.85,cos58°≈0.53,tan58°≈1.60.
能力提升
13.如图,在△ABC中, 则AC的长为( )
14.如图,在矩形ABCD中,BD是对角线,AE⊥BD,垂足为E,连接CE,若 则tan∠DEC的值是_____________.
15.如图,在Rt△ABC中,∠C=90°,sinB=;D在BC边上,且∠ADC=45°,AC=5,求∠BAD的正切值.
16.[数学抽象]已知锐角△中,角A、B、C的对边分别为a、b、c,边角总满足关系式: .
(1)如图1,若 求b的值;
(2)某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD(如图2所示),若 米,AB=10米, 求景观桥CD的长度.
参考答案
基础过关
1.B 直角三角形中,已知直角的条件下,再知道一边一锐角,或两边,则直角三角形可解,四个选项中,只有B项的条件可解直角三角形,故选B.
2.答案
解析 在Rt△ABC中,
3.解析 在 中,
4.解析 (1)在Rt△ABC中,
(2)在 中,
(3)在Rt△ABC中,
(4)在Rt△ABC中,
(5)在 中,
∴
5.解析
6.解析 (1)根据题意作图,连接BD,则BD=CD.
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC.
∵AB=CE,∴△ABD的周长=AC+CE=AE=1.
故△ABD的周长为1.
∴设则
∵BD=CD,∴AC=AD+CD=4x.
在Rt△ABD中,
7.D 点A作ADLBC,垂足为D,如图所示.
在Rt△ACD中,CD=CA·cosC=∴ 在Rt△ABD中,
故选D.
8.A 如图,过点A作AD⊥BC于点D,则AD=h ,过点P作PE⊥QR交QR的延长线于点E,则PE=h ,
在Rt△ADC中, 在 中,h =PE=5×sin55°,∴h =h ,故选A.
9.答案 4
解析 如图,过点A作 垂足为D.
在 中,∵AC=
在中, 故填4.
10.解析 (1)如图,过点B作BC⊥OA于点C.
在Rt△BOC中,∠OCB=90°,OB=5,sin∠AOB=,∴,∴.
∴点B的坐标为(4,3).
(2)∵点A的坐标为(10,0),∴OA=10.∴AC=OA-OC=10-4=6.
11.解析 如图,过点B作BDLAC,交AC的延长线于点D,由题意得∠BCD=45°.
12.解析 如图,过点A作AD⊥BC,垂足为D.
∵∠ACB=45°,∴AD=CD.设
在Rt△ADB中,AD=AB·sin58°≈0.85xm,BD=AB·cos58°≈0.53x m.
∵BC=221m,即CD+BD=221m,∴0.85x+0.53x=221,∴x≈160.
答:AB的长约为160m.
能力提升
13.B 如图,过点A作AD⊥BC于D,则∠ADC=∠ADB=90°.
故选B.
14.答案
解析 如图,过点C作CF⊥BD于点F.
∵四边形ABCD是矩形,∴AB=CD,AB∥CD.∴∠ABE=∠CDF.
∵AE⊥BD,∴∠AEB=∠CFD=90°.∴△ABE≌△CDF(AAS).∴AE=CF,BE=FD.
∵AE⊥BD,,∴设,则.
故填
15.解析 如图,过点D作DE⊥AB于点E.
在 中,
在 中, ∠C=90°,∵ 即
根据勾股定理,得 ∴BD=BC-DC=12-5=7.
在Rt△BDE中,
在Rt△AED中,根据勾股定理,得AE=
16.解析 (1)∵∠B=45°,∠C=75°,∴∠A=60°.
即
(舍去).
∴CD的长度为8米.
