2022-2023学年北师大版八年级数学上册 第1章 勾股定理 (填空题) 专题达标测评(Word版,含解析)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学上册 第1章 勾股定理 (填空题) 专题达标测评(Word版,含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览


文档简介
2022-2023学年北师大版八年级数学上册《第1章勾股定理》填空题专题达标测评(附答案)
(共20小题,每小题6分,满分120分)
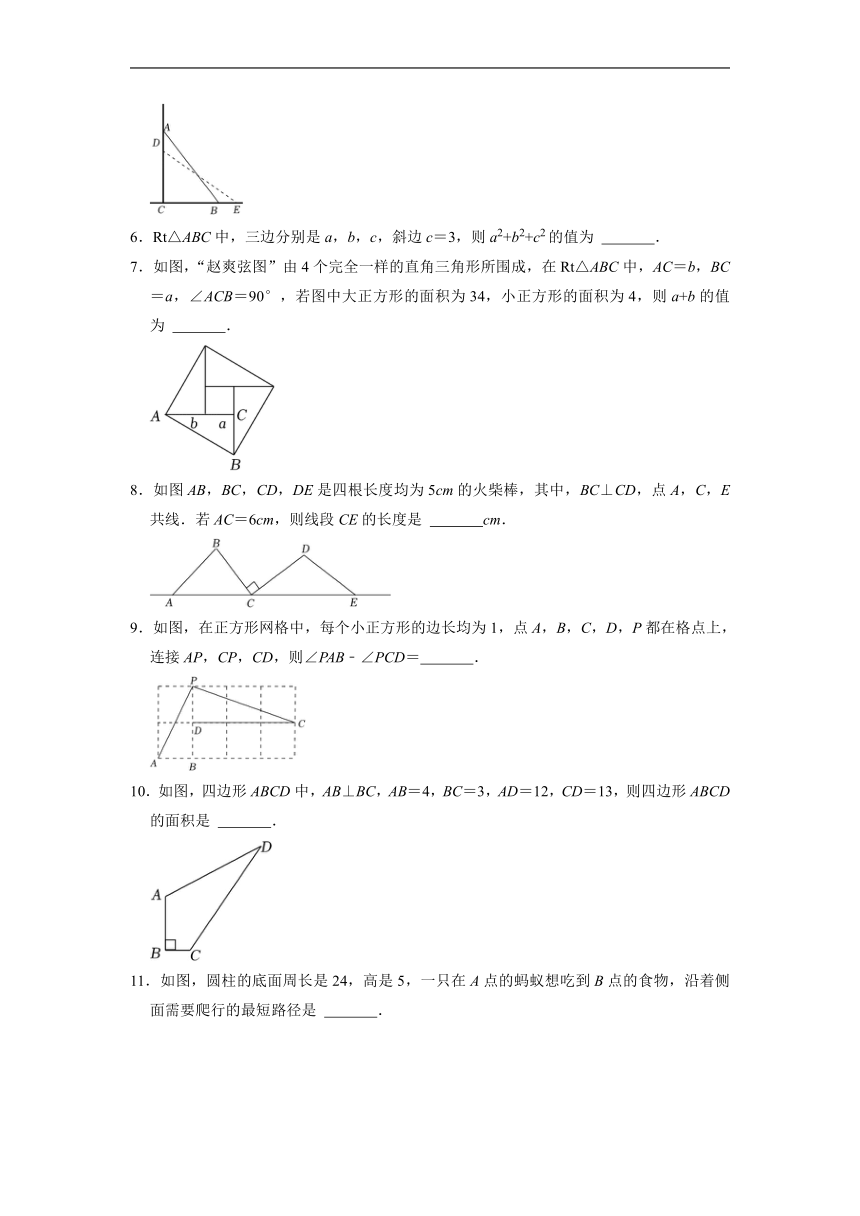
1.在Rt△ACB中,∠C=90°,AD平分∠BAC交BC于点D.若AB=10,AC=6,BD=5,则点D到AB的距离是 .
2.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3= .
3.如图,将一根长12cm的筷子置于底面半径为3cm,高为8cm的圆柱形杯子中,则筷子露在杯子外面的长度h的取值范围为 cm.
4.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AB=3,CD=2,则AD2+BC2= .
5.如图,一架10m长的梯子AB斜靠在一竖直的墙AC上,底端离墙的距离BC为6m,当梯子下滑到DE时,AD=2m,则BE= m.
6.Rt△ABC中,三边分别是a,b,c,斜边c=3,则a2+b2+c2的值为 .
7.如图,“赵爽弦图”由4个完全一样的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为34,小正方形的面积为4,则a+b的值为 .
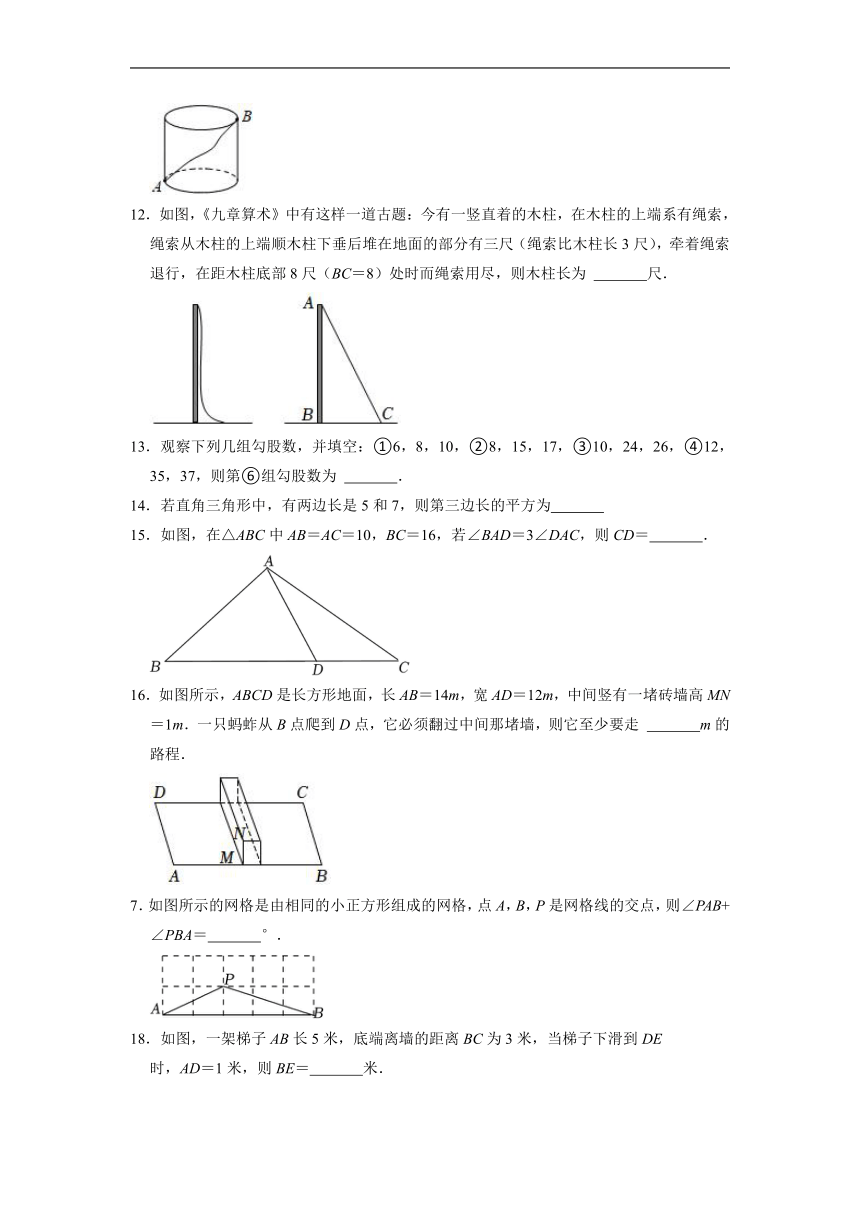
8.如图AB,BC,CD,DE是四根长度均为5cm的火柴棒,其中,BC⊥CD,点A,C,E共线.若AC=6cm,则线段CE的长度是 cm.
9.如图,在正方形网格中,每个小正方形的边长均为1,点A,B,C,D,P都在格点上,连接AP,CP,CD,则∠PAB﹣∠PCD= .
10.如图,四边形ABCD中,AB⊥BC,AB=4,BC=3,AD=12,CD=13,则四边形ABCD的面积是 .
11.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁想吃到B点的食物,沿着侧面需要爬行的最短路径是 .
12.如图,《九章算术》中有这样一道古题:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC=8)处时而绳索用尽,则木柱长为 尺.
13.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑥组勾股数为 .
14.若直角三角形中,有两边长是5和7,则第三边长的平方为
15.如图,在△ABC中AB=AC=10,BC=16,若∠BAD=3∠DAC,则CD= .
16.如图所示,ABCD是长方形地面,长AB=14m,宽AD=12m,中间竖有一堵砖墙高MN=1m.一只蚂蚱从B点爬到D点,它必须翻过中间那堵墙,则它至少要走 m的路程.
7.如图所示的网格是由相同的小正方形组成的网格,点A,B,P是网格线的交点,则∠PAB+∠PBA= °.
18.如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE
时,AD=1米,则BE= 米.
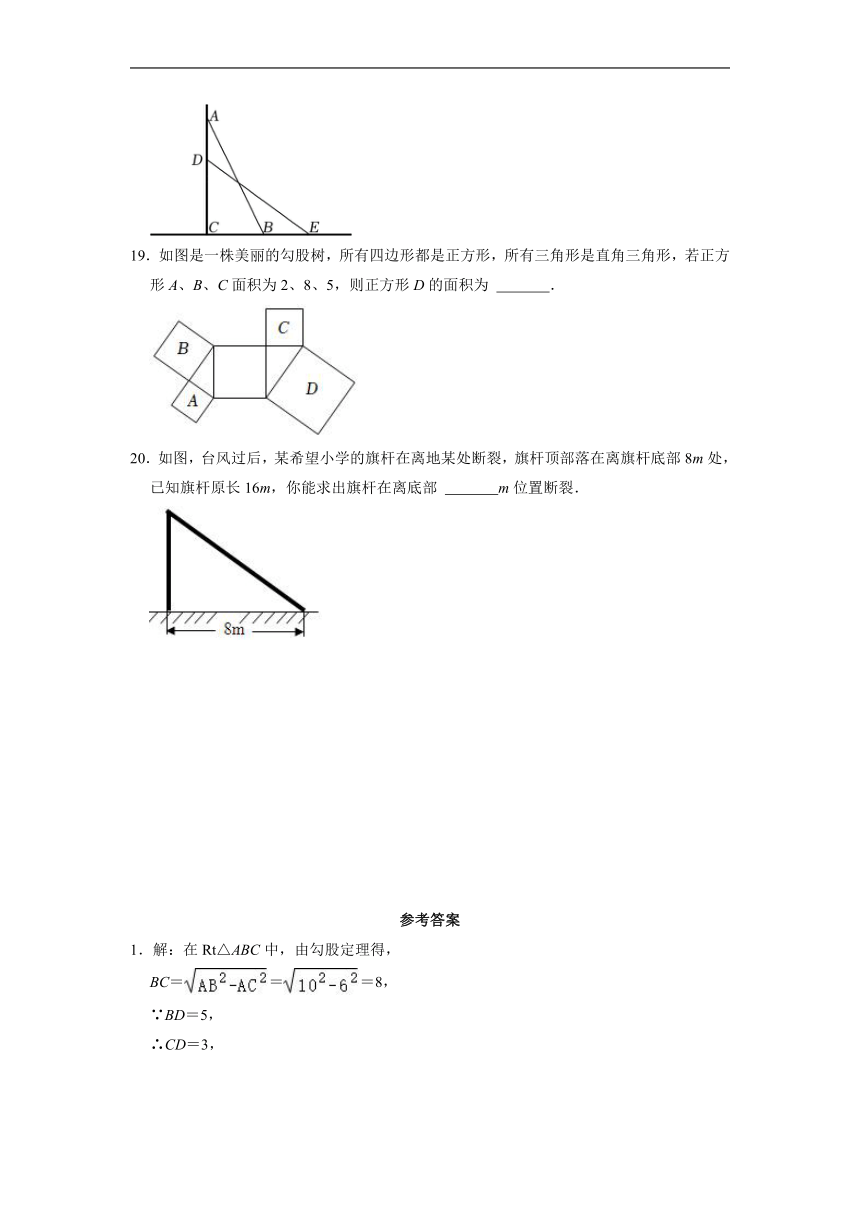
19.如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为 .
20.如图,台风过后,某希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8m处,已知旗杆原长16m,你能求出旗杆在离底部 m位置断裂.
参考答案
1.解:在Rt△ABC中,由勾股定理得,
BC===8,
∵BD=5,
∴CD=3,
过点D作DE⊥AB于E,
∵AD平分∠BAC,
∴CD=DE=3,
∴点D到AB的距离是3,
故答案为:3.
2.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故答案为:7.
3.解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=12﹣8=4(cm);
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=6cm,BD=8cm,
∴AB===10(cm),
∴此时h=12﹣10=2(cm),
所以h的取值范围是:2cm≤h≤4cm.
故答案为:2cm≤h≤4.
4.解:∵BD⊥AC,
∴∠COB=∠AOB=∠AOD=∠COD=90°,
在Rt△AOB和Rt△COD中,根据勾股定理得,
BO2+AO2=AB2=32=9,OD2+OC2=CD2=22=4,
∴BO2+AO2+OD2+OC2=9+4=13,
∵AD2=DO2+AO2,BC2=OC2+BO2,
∴AD2+BC2=13.
故答案为:13.
5.解:在Rt△ABC中,根据勾股定理,可得:AC===8(米),
∴DC=AC﹣AD=8﹣2=6(米),
在Rt△DCE中,CE===8(米),
∴BE=CE﹣BC=8﹣6=2(米),
故答案为:2.
6.解:∵△ABC为直角三角形,斜边c=3,
∴a2+b2=c2=32=9,
∴a2+b2+c2=9+9=18.
故答案为:18.
7.解:∵大正方形的面积为34,小正方形的面积为4,
∴a2+b2=34,(b﹣a)2=4,
∴4×ab=34﹣4=30,
∴2ab=30,
∴(a+b)2=(b﹣a)2+4ab=4+60=64,
∴a+b=8.
故答案为:8.
8.解:作BG⊥AC,DH⊥CE,垂足分别为G、H,
∴∠BGC=∠DHC=90°,
∴∠BCG+∠CBG=90°,
∵CD⊥BC,
∴∠BCD=90°,
∴∠BCG+∠DCH=90°,
∴∠CBG=∠DCH,
在△BCG和△CDH中,
,
∴△BCG≌△CDH(AAS),
∴BG=CH,
∵AB=BC,BG⊥AC,AC=6,
∴CG=AC=3,
∴BM=CN,
在Rt△BCG中,
由勾股定理得:BG=,
∴CH=4,
∵CD=DE,DH⊥CE,
∴CH=EH,
∴CE=CH+EH=8,
故答案为:8.
9.解:如图所示:连接AE,PE,
则△PCD≌△EAF,
所以∠PCD=∠EAF,
∴∠PAB﹣∠PCD=∠PAB﹣∠EAF=∠PAE,
∵由勾股定理得:AP2=PE2=22+12=5,AE2=32+12=10,
∴AP2+PE2=AE2,
∴△PAE是等腰直角三角形,
∴∠PAE=45°,
即∠PAB﹣∠PCD=∠PAE=45°,
故答案为:45°.
10.解:如图,连接AC,
在△ABC中,AB⊥BC,AB=4,BC=3,
∴AC===5.
在△ADC中,AD=12,CD=13,AC=5.
∵122+52=132,即AD2+AC2=CD2,
∴△ADC是直角三角形,且∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ADC
=AB BC+AC AD
=×4×3+×5×12
=6+30
=36.
故答案为:36.
11.解:展开圆柱的半个侧面是矩形,
矩形的长是圆柱的底面周长的一半,即为12,矩形的宽是圆柱的高5.
根据两点之间线段最短,
知最短路程是矩形的对角线的长,即=13,
故答案为:13.
12.解:设木柱长为x尺,根据题意得:
AB2+BC2=AC2,
则x2+82=(x+3)2,
解得:x=.
答:木柱长为尺.
故答案为:.
13.解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+1),第二个是:n(n+2),第三个数是:(n+1)2+1,
故可得第⑦组勾股数是16,63,65.
故答案为选:16,63,65.
14.解:①若7是直角边,则第三边x是斜边,由勾股定理,得x=;
②若7是斜边,则第三边x为直角边,由勾股定理,得x=;
故x2=74或24.
故答案为:74或24.
15.解:作AE⊥BC于点E,作DF⊥AC于点F,如图所示,
∵AB=AC=10,BC=16,
∴CE=8,
∴AD===6,
设∠CAD=x,则∠CAD=3x,
∵AE⊥BC,AB=AC,
∴∠BAE=∠CAE=2x,
∴∠EAD=∠DAC,
∴DE=DF,
设CD=a,则DE=8﹣a,
∵,
∴,
解得a=5,
即CD=5,
故答案为:5.
16.解:连接BD,如图所示,将图展开,图形长度增加2个MN的长度,
即原图长度增加2米,
∴BD=14+2=16(米),
连接AC,
∵四边形ABCD是长方形,BD=16米,宽CD=12米,
在Rt△BDC中,由勾股定理得:
BD===20(米),
∴蚂蚱从B点爬到D点,它至少要走20米的路程.
故答案为:20.
17.解:延长AP交格点于D,连接BD,
则PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,
∴∠PDB=90°,
∴∠DPB=∠PAB+∠PBA=45°.
故答案为:45.
18.解:在Rt△ABC中,根据勾股定理,可得:AC===4(米),
∴DC=AC﹣AD=4﹣1=3(米),
在Rt△DCE中,CE===4(米),
∴BE=CE﹣BC=4﹣3=1(米),
故答案为:1.
19.解:由勾股定理得,正方形D的面积=正方形A的面积+正方形B的面积+正方形C面积=2+8+5=15,
故答案为:15.
20.解:设旗杆在离底部x米的位置断裂,在给定图形上标上字母如图所示.
∵AB=x米,AB+AC=16米,
∴AC=(16﹣x)米.
在Rt△ABC中,AB=x米,AC=(16﹣x)米,BC=8米,
∴AC2=AB2+BC2,即(16﹣x)2=x2+82,
解得:x=6.
故旗杆在离底部6米的位置断裂.
故答案为:6.
(共20小题,每小题6分,满分120分)
1.在Rt△ACB中,∠C=90°,AD平分∠BAC交BC于点D.若AB=10,AC=6,BD=5,则点D到AB的距离是 .
2.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3= .
3.如图,将一根长12cm的筷子置于底面半径为3cm,高为8cm的圆柱形杯子中,则筷子露在杯子外面的长度h的取值范围为 cm.
4.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AB=3,CD=2,则AD2+BC2= .
5.如图,一架10m长的梯子AB斜靠在一竖直的墙AC上,底端离墙的距离BC为6m,当梯子下滑到DE时,AD=2m,则BE= m.
6.Rt△ABC中,三边分别是a,b,c,斜边c=3,则a2+b2+c2的值为 .
7.如图,“赵爽弦图”由4个完全一样的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为34,小正方形的面积为4,则a+b的值为 .
8.如图AB,BC,CD,DE是四根长度均为5cm的火柴棒,其中,BC⊥CD,点A,C,E共线.若AC=6cm,则线段CE的长度是 cm.
9.如图,在正方形网格中,每个小正方形的边长均为1,点A,B,C,D,P都在格点上,连接AP,CP,CD,则∠PAB﹣∠PCD= .
10.如图,四边形ABCD中,AB⊥BC,AB=4,BC=3,AD=12,CD=13,则四边形ABCD的面积是 .
11.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁想吃到B点的食物,沿着侧面需要爬行的最短路径是 .
12.如图,《九章算术》中有这样一道古题:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC=8)处时而绳索用尽,则木柱长为 尺.
13.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑥组勾股数为 .
14.若直角三角形中,有两边长是5和7,则第三边长的平方为
15.如图,在△ABC中AB=AC=10,BC=16,若∠BAD=3∠DAC,则CD= .
16.如图所示,ABCD是长方形地面,长AB=14m,宽AD=12m,中间竖有一堵砖墙高MN=1m.一只蚂蚱从B点爬到D点,它必须翻过中间那堵墙,则它至少要走 m的路程.
7.如图所示的网格是由相同的小正方形组成的网格,点A,B,P是网格线的交点,则∠PAB+∠PBA= °.
18.如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE
时,AD=1米,则BE= 米.
19.如图是一株美丽的勾股树,所有四边形都是正方形,所有三角形是直角三角形,若正方形A、B、C面积为2、8、5,则正方形D的面积为 .
20.如图,台风过后,某希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8m处,已知旗杆原长16m,你能求出旗杆在离底部 m位置断裂.
参考答案
1.解:在Rt△ABC中,由勾股定理得,
BC===8,
∵BD=5,
∴CD=3,
过点D作DE⊥AB于E,
∵AD平分∠BAC,
∴CD=DE=3,
∴点D到AB的距离是3,
故答案为:3.
2.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故答案为:7.
3.解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=12﹣8=4(cm);
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=6cm,BD=8cm,
∴AB===10(cm),
∴此时h=12﹣10=2(cm),
所以h的取值范围是:2cm≤h≤4cm.
故答案为:2cm≤h≤4.
4.解:∵BD⊥AC,
∴∠COB=∠AOB=∠AOD=∠COD=90°,
在Rt△AOB和Rt△COD中,根据勾股定理得,
BO2+AO2=AB2=32=9,OD2+OC2=CD2=22=4,
∴BO2+AO2+OD2+OC2=9+4=13,
∵AD2=DO2+AO2,BC2=OC2+BO2,
∴AD2+BC2=13.
故答案为:13.
5.解:在Rt△ABC中,根据勾股定理,可得:AC===8(米),
∴DC=AC﹣AD=8﹣2=6(米),
在Rt△DCE中,CE===8(米),
∴BE=CE﹣BC=8﹣6=2(米),
故答案为:2.
6.解:∵△ABC为直角三角形,斜边c=3,
∴a2+b2=c2=32=9,
∴a2+b2+c2=9+9=18.
故答案为:18.
7.解:∵大正方形的面积为34,小正方形的面积为4,
∴a2+b2=34,(b﹣a)2=4,
∴4×ab=34﹣4=30,
∴2ab=30,
∴(a+b)2=(b﹣a)2+4ab=4+60=64,
∴a+b=8.
故答案为:8.
8.解:作BG⊥AC,DH⊥CE,垂足分别为G、H,
∴∠BGC=∠DHC=90°,
∴∠BCG+∠CBG=90°,
∵CD⊥BC,
∴∠BCD=90°,
∴∠BCG+∠DCH=90°,
∴∠CBG=∠DCH,
在△BCG和△CDH中,
,
∴△BCG≌△CDH(AAS),
∴BG=CH,
∵AB=BC,BG⊥AC,AC=6,
∴CG=AC=3,
∴BM=CN,
在Rt△BCG中,
由勾股定理得:BG=,
∴CH=4,
∵CD=DE,DH⊥CE,
∴CH=EH,
∴CE=CH+EH=8,
故答案为:8.
9.解:如图所示:连接AE,PE,
则△PCD≌△EAF,
所以∠PCD=∠EAF,
∴∠PAB﹣∠PCD=∠PAB﹣∠EAF=∠PAE,
∵由勾股定理得:AP2=PE2=22+12=5,AE2=32+12=10,
∴AP2+PE2=AE2,
∴△PAE是等腰直角三角形,
∴∠PAE=45°,
即∠PAB﹣∠PCD=∠PAE=45°,
故答案为:45°.
10.解:如图,连接AC,
在△ABC中,AB⊥BC,AB=4,BC=3,
∴AC===5.
在△ADC中,AD=12,CD=13,AC=5.
∵122+52=132,即AD2+AC2=CD2,
∴△ADC是直角三角形,且∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ADC
=AB BC+AC AD
=×4×3+×5×12
=6+30
=36.
故答案为:36.
11.解:展开圆柱的半个侧面是矩形,
矩形的长是圆柱的底面周长的一半,即为12,矩形的宽是圆柱的高5.
根据两点之间线段最短,
知最短路程是矩形的对角线的长,即=13,
故答案为:13.
12.解:设木柱长为x尺,根据题意得:
AB2+BC2=AC2,
则x2+82=(x+3)2,
解得:x=.
答:木柱长为尺.
故答案为:.
13.解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+1),第二个是:n(n+2),第三个数是:(n+1)2+1,
故可得第⑦组勾股数是16,63,65.
故答案为选:16,63,65.
14.解:①若7是直角边,则第三边x是斜边,由勾股定理,得x=;
②若7是斜边,则第三边x为直角边,由勾股定理,得x=;
故x2=74或24.
故答案为:74或24.
15.解:作AE⊥BC于点E,作DF⊥AC于点F,如图所示,
∵AB=AC=10,BC=16,
∴CE=8,
∴AD===6,
设∠CAD=x,则∠CAD=3x,
∵AE⊥BC,AB=AC,
∴∠BAE=∠CAE=2x,
∴∠EAD=∠DAC,
∴DE=DF,
设CD=a,则DE=8﹣a,
∵,
∴,
解得a=5,
即CD=5,
故答案为:5.
16.解:连接BD,如图所示,将图展开,图形长度增加2个MN的长度,
即原图长度增加2米,
∴BD=14+2=16(米),
连接AC,
∵四边形ABCD是长方形,BD=16米,宽CD=12米,
在Rt△BDC中,由勾股定理得:
BD===20(米),
∴蚂蚱从B点爬到D点,它至少要走20米的路程.
故答案为:20.
17.解:延长AP交格点于D,连接BD,
则PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,
∴∠PDB=90°,
∴∠DPB=∠PAB+∠PBA=45°.
故答案为:45.
18.解:在Rt△ABC中,根据勾股定理,可得:AC===4(米),
∴DC=AC﹣AD=4﹣1=3(米),
在Rt△DCE中,CE===4(米),
∴BE=CE﹣BC=4﹣3=1(米),
故答案为:1.
19.解:由勾股定理得,正方形D的面积=正方形A的面积+正方形B的面积+正方形C面积=2+8+5=15,
故答案为:15.
20.解:设旗杆在离底部x米的位置断裂,在给定图形上标上字母如图所示.
∵AB=x米,AB+AC=16米,
∴AC=(16﹣x)米.
在Rt△ABC中,AB=x米,AC=(16﹣x)米,BC=8米,
∴AC2=AB2+BC2,即(16﹣x)2=x2+82,
解得:x=6.
故旗杆在离底部6米的位置断裂.
故答案为:6.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
