2022-2023学年苏科版八年级数学上册 第2章 轴对称图形 同步解答专项练习题(Word版,含解析)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册 第2章 轴对称图形 同步解答专项练习题(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 580.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 14:37:36 | ||
图片预览



文档简介
2022-2023学年苏科版八年级数学上册《第2章轴对称图形》同步解答专项练习题(附答案)
1.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
2.如图,在Rt△ABC中,∠ACB=90°,D是AB边的中点,DE⊥AC,垂足为点E,连接DC.
(1)若∠A=36°,求∠BCD的度数;
(2)若∠A=30°,DE+BC=6,求DE和EC的长.
3.如图,已知△ABC,AD是∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.
(1)求证:AD垂直平分EF;
(2)若AB+AC=10,DE=3,求△ABC的面积.
4.如图,△ABC和△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)图中点C的对应点是点 ,∠B的对应角是 ;
(2)若DE=5,BF=2,则CF的长为 ;
(3)若∠BAC=108°,∠BAE=30°,求∠EAF的度数.
5.如图,直线EF分别交直线AB、CD于点E、F,EP平分∠AEF交CD于点P,点N是射线PC上一点,延长EP到点M,使得PM=PN,连接MN.
(1)若AB∥CD,∠EFD=80°,求∠AEP的度数;
(2)若∠PMN=72.5°,∠AEF=70°,判断直线AB与CD是否平行?并说明理由.
6.如图,在四边形ABCD中,DE垂直平分AB,DF垂直平分BC,垂足分别为E,F.
(1)试说明DA=DC;
(2)如果∠A=70°,∠C=60°,求∠ADC的度数.
7.如图,在△ABC中,AD平分∠BAC,过点B作AD的垂线,垂足为点D,DE∥AC,交AB于点E,CD∥AB.
(1)求证:△BDE是等腰三角形;
(2)求证:CD=BE.
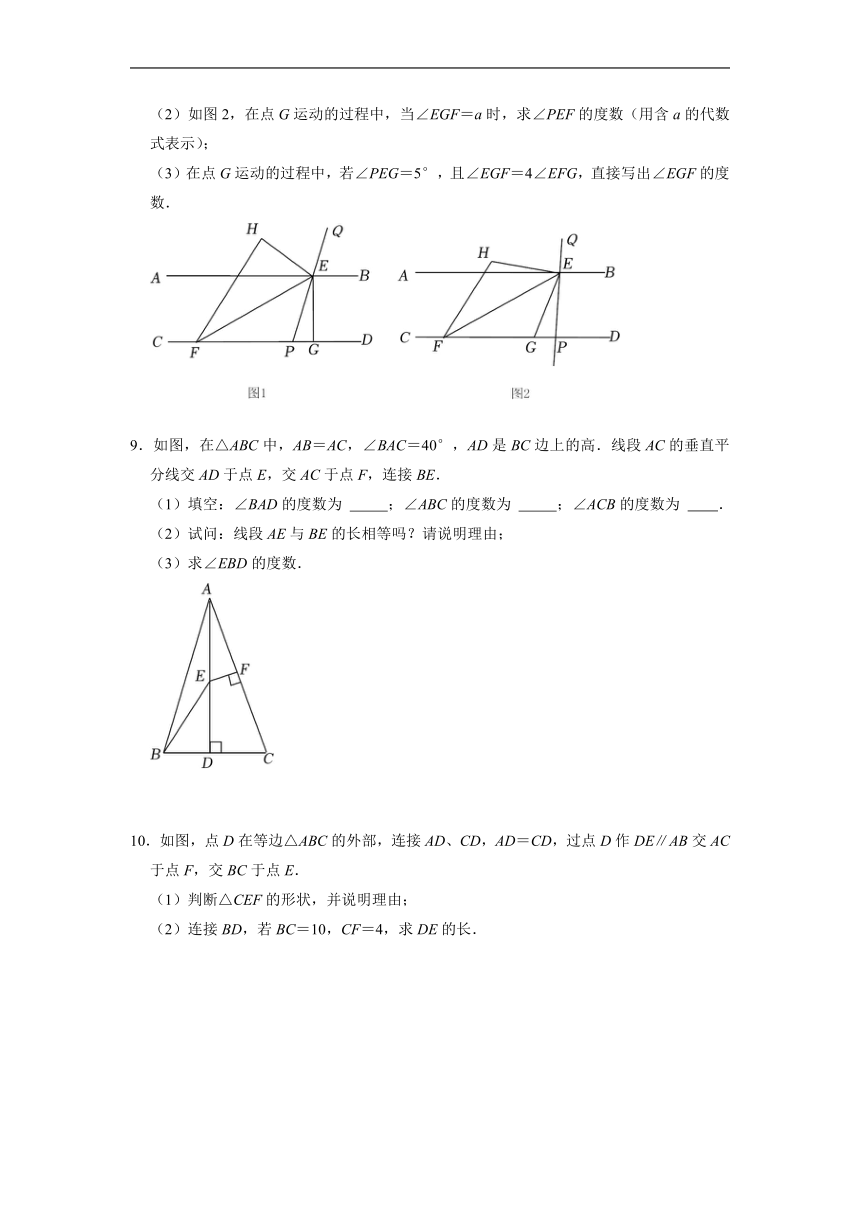
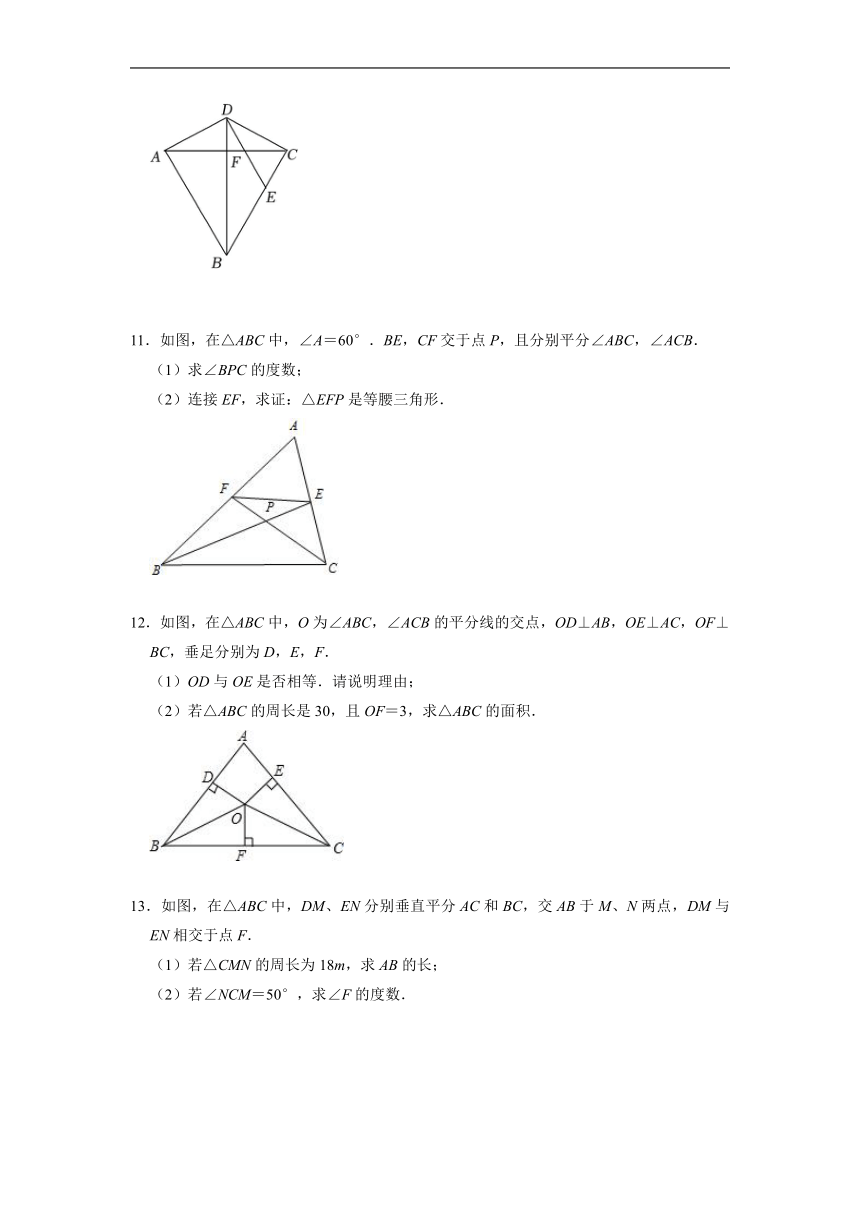
8.如图1,已知直线AB∥CD,点E、F分别在直线AB、CD上,G点为射线FD上一动点,且∠FEG>∠EFG,将△EFG沿着EF翻折得到△EFH,直线EQ平分∠BEH交直线CD于点P.
(1)当EG⊥CD时,
①若∠EFG=30°,则∠PEF= .
②若去掉条件“∠EFG=30°”,你还能求出∠PEF的度数吗?试一试.
(2)如图2,在点G运动的过程中,当∠EGF=a时,求∠PEF的度数(用含a的代数式表示);
(3)在点G运动的过程中,若∠PEG=5°,且∠EGF=4∠EFG,直接写出∠EGF的度数.
9.如图,在△ABC中,AB=AC,∠BAC=40°,AD是BC边上的高.线段AC的垂直平分线交AD于点E,交AC于点F,连接BE.
(1)填空:∠BAD的度数为 ;∠ABC的度数为 ;∠ACB的度数为 .
(2)试问:线段AE与BE的长相等吗?请说明理由;
(3)求∠EBD的度数.
10.如图,点D在等边△ABC的外部,连接AD、CD,AD=CD,过点D作DE∥AB交AC于点F,交BC于点E.
(1)判断△CEF的形状,并说明理由;
(2)连接BD,若BC=10,CF=4,求DE的长.
11.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
12.如图,在△ABC中,O为∠ABC,∠ACB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F.
(1)OD与OE是否相等.请说明理由;
(2)若△ABC的周长是30,且OF=3,求△ABC的面积.
13.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为18m,求AB的长;
(2)若∠NCM=50°,求∠F的度数.
14.如图,在△ABC中,点D是BC上的点,AD=BD,将△ABD沿AD翻折得到
△AED,若∠B=40°,求∠CDE的度数.
15.在图示的正方形网格纸中,每个小正方形的边长都是1,△ABC的三个顶点都在小正方形的顶点处,直线MN与网格中竖直的线相重合.
(1)直接写出△ABC的面积;
(2)作出△ABC关于直线MN对称的△A'B'C';
(3)在网格内找一点D,使点D到线段BC,B'C'的距离相等且DB=DC.(在网格上直接标出点D的位置,不写作法)
16.如图,在△ABC中,∠C=90°,点M,N分别在边AB,BC上,且点A,B关于直线MN对称,连接AN.
(1)若∠CAN=α,则∠B与α之间的数最关系为 ;
(2)若,,且△ABC的周长为24.求△ACN的周长.
17.如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是点D,连结CD交OA于点M,交OB于点N.
(1)①若∠AOB=60°,求∠COD的度数.
②若∠AOB=n°,则∠COD= °(用含n的代数式表示).
(2)若CD=4,则△PMN的周长为 .
18.如图,由4个小正方形组成的田字格,△ABC的顶点都是小正方形的顶点,请在下列三个田字格中分别画出与△ABC成轴对称,且顶点都在小正方形顶点上的三角形(要求三个图互不相同).
19.如图,大海中有两个岛屿A与B,∠BEQ=30°,在海岸线PQ上的点F处测得∠AFP=60°,∠BFQ=60°.
(1)求证:AE=AB;
(2)若在海岸线PQ上的点E处测得∠AEP=74°,求∠BAE的度数.
20.旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相部的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系(直接写出结论).
参考答案
1.(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CEF=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=(180°﹣50°)=65°,
∴∠DEF=65°.
2.解:(1)∵∠ACB=90°,D是AB边的中点,
∴AD=CD=BD,
∴∠A=∠DCA=36°,
∴∠BCD=90°﹣36°=54°.
(2)由(1)得,∠A=∠DCA=30°,
∵DE⊥AC,
∴∠DEC=90°,
∴DE=,
∵∠A=30°,∠ACB=90°,
∴∠B=60°,
∴△DCB是等边三角形,
∴CD=BC=2DE,
又∵DE+BC=6,
∴DE=2,BC=DC=4,
∴EC=.
3.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠DEA=∠DFA=90°,
∵AD是∠BAC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD是∠BAC的角平分线,
∴AG⊥EF,EG=FG,
∴AD垂直平分EF;
(2)解:∵AD是∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵DE=3,
∴DF=3,
∵AB+AC=10,
∴△ABC的面积=
==15.
4.解:(1)∵△ABC与△ADE关于直线MN对称,
∴图中点C的对应点是点E,∠B的对应角是∠D;
故答案为:E,∠D.
(2)∵△ABC与△ADE关于直线MN对称,
∴△ABC≌△ADE,
∴BC=DE=5,
∴CF=BC﹣BF=3.
故答案为:3.
(3)∵∠BAC=108°,∠BAE=30°,
∴∠CAE=108°﹣30°=78°,
再根据对称性,
∴∠EAF=∠CAF,
∴∠EAF==39°.
5.解:(1)∵AB∥CD,∠EFD=80°,
∴∠AEF=∠EFD=80°,
∵EP平分∠AEF,
∴∠AEP=∠AEF=40°;
(2)AB∥CD,
理由:∵PN=PM,∠PMN=72.5°,
∴∠PNM=∠PMN=72.5°,
∴∠MPN=35°,
∴∠EPF=∠MPN=35°,
∵EM平分∠AEF,∠AEF=70°,
∴∠AEM=∠AEF=35°,
∴∠AEM=∠EPF,
∴AB∥CD.
6.解:(1)如图,连接DB,
∵DE垂直平分AB,DF垂直平分BC,
∴DA=DB,DC=DB,
∴DA=DC;
(2)∵DA=DB,∠A=70°,
∴∠DBA=∠A=70°,
∵DC=DB,∠C=60°,
∴∠DBC=∠C=60°,
∴∠ABC=∠DBA+∠DBC=130°,
∵∠A+∠ABC+∠C+∠ADC=360°,
∴∠ADC=100°.
7.证明:(1)∵DE∥AC,∠1=∠2,
∴∠1=∠2=∠3=∠4,
∵∠2+∠ABD=90°,∠5+∠4=90°,
∴∠5=∠ABD,
∴DE=BE,
∴△BDE是等腰三角形;
(2)由(1)知,∠4=∠2,
∴AE=DE,
∵AD=AD,∠1=∠4,∠2=∠3,
∴△ACD≌△AED(ASA),
∴CD=AE,
∴CD=AE=DE=BE.
8.解:(1)当EG⊥CD时,∠EGF=90°,
①若∠EFG=30°,则∠FEG=60°,
由翻折可知:∠FEH=CFEG=60°,
∵AB∥CD,
∴∠AEF=∠EFG=30°,
∴∠AEH=∠FEH﹣∠AEF=30°,
∴∠BEH=180°﹣∠AEH=150°,
∵EQ平分∠BEH,
∴∠BEQ=∠BEH=75°,
∴∠AEP=∠BEQ=75°,
∴∠PEF=∠AEP﹣∠AEF=45°,
故答案为:45°;
②若去掉条件“∠EFG=30°“,还能求出∠PEF的度数,
∵∠EGF=90°,
∴∠EFG+∠FEG=90°,
由翻折可知:∠FEH=∠FEG,
∵AB//CD,
∴∠AEF=∠EFG,
∴∠AEH=∠FEH﹣∠AEF=∠FEG﹣∠EFG,
∴∠BEH=180°﹣∠AEH=180°﹣∠FEG+∠EFG,
∵EQ平分∠BEH,
∴∠BEQ=∠BEH=90°﹣∠FEG+∠EFG,
∴∠AEP=∠BEQ=90°﹣∠FEG+∠EFG,
∴∠PEF=∠AEP﹣∠AEF=90°﹣∠FEG+∠EFG﹣∠EFG
=90°﹣∠FEG﹣∠EFG
=90°﹣(∠FEG+∠EFG)
=90°﹣45°
=45°;
(2)在点G运动的过程中,当∠EGF=a时,
∠EFG+∠FEG=180°﹣a,
由翻折可知:∠FEH=∠FEG,
∵AB∥CD,
∴∠AEF=∠EFG,
∴∠AEH=∠FEH﹣∠AEF=CFEG﹣∠EFG,
∴∠BEH=180°﹣∠AEH=180°﹣∠FEG+∠EFG,
∵EQ平分∠BEH,
∴∠BEQ=∠BEH=90°﹣∠FEG+∠EFG,
∴∠AEP=∠BEQ=90°﹣∠FEG+∠EFG,
∴∠PEF=∠AEP﹣∠AEF=90°﹣∠FEG+∠EFG﹣∠EFG
=90°﹣∠FEG﹣∠EFG
=90°﹣(∠FEG+∠EFG)
=90°﹣(180°﹣a)
=a,
即∠PEF的度数为α;
(3)由(2)知:在点G运动的过程中,
∠PEF=∠EGF,
在点G运动的过程中,若∠PEG=5°,且∠EGF=4∠EFG,
则∠EFG=∠EGF,
点G在点P的右侧时,
∠FEG=∠PEF+∠PEG=∠EGF+5°
∵∠EGF+∠EFG+∠FEG=180°,
∴∠EGF+∠EGF+∠EGF﹣5°=180°
解得:∠EGF=,
综上所述,∠EGF的度数为100°或.
9.解:(1)∵AB=AC,∠BAC=40°,AD是BC边上的高,
∴∠BAD=∠CAD=∠BAC=20°,∠ACB=∠ABC=(180°﹣∠BAC)=×(180°﹣40°)=70°,
故答案为:20°,70°,70°;
(2)线段AE与BE的长相等,理由如下:
如图,连接CE,
∵AB=AC,AD是BC边上的高,
∴BD=CD,AD⊥BC,
∴BE=CE,
∵EF是线段AC的垂直平分线,
∴AE=CE,
∴AE=BE;
(3)由(2)可知,∠ABC=70°,AE=BE,
∴∠ABE=∠BAD=20°,
∴∠EBD=∠ABC﹣∠ABE=70°﹣20°=50°.
10.解:(1)△CEF是等边三角形,理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵AB∥DE,
∴∠CEF=∠ABC=60°,
∴∠CEF=∠CFE=∠ECF=60°,
∴△CEF是等边三角形;
(2)∵△ABC是等边三角形,△CEF是等边三角形,
∴AB=BC,CF=CE=4.
∵AD=CD,
∴BD是线段AC的垂直平分线,
∴BD平分∠ABC,
∴∠ABD=∠CBD.
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠BDE=∠CBD,
∴BE=DE.
∵BC=BE+EC=DE+CF,
∴DE=BC﹣CF=10﹣4=6.
11.(1)解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=ABC,,
∴∠CBE+∠BCF=∠ABC+ACB==60°,
∴∠BPC=180°﹣(∠CBE+∠BCF)=180°﹣60°=120°;
(2)证明:在BC上截取BQ=BF,连接PQ,
在△FBP和△QBP中,
,
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°﹣60°﹣120°=180°,
∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP,
在△CQP和△CEP中,
,
∴△CQP≌△CEP(AAS),
∴EF=QP,
∵FP=EP,
∴△EFP是等腰三角形.
12.解:(1)OD=OE,
理由:∵O为∠ABC,∠ACB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,
∴OD=OF,OF=OE,
∴OD=OE;
(2)连接OA,
∴△ABC的面积=S△AOB+S△BOC+S△AOC=AB OD+BC OF+AC OE,
∵OE=OD=OF,
∴△ABC的面积=(AB+BC+AC) OF=×30×3=45.
13.(1)解:∵DM、EN分别垂直平分AC和BC,
∴MA=MC,BN=CN,
∵△CMN的周长为18m,
∴CM+MN+CN=18m,
∴AB=AM+MN+BN=CM+MN+CN=18m;
(2)解:∵DM、EN分别垂直平分AC和BC,
∴MA=MC,BN=CN,
∴∠MCA=∠A,∠NCB=∠B,
∵∠A+∠B+∠ACB=∠A+∠B+∠NCB+∠NCM+∠MCA=180°,
∴2∠A+2∠B+∠NCM=180°,
即2∠A+2∠B+50°=180°,
∴∠A+∠B=65°,
∵DM⊥AC,EN⊥BC,
∴∠A+∠AMD=90°,∠B+∠BNE=90°,
∴∠AMD+∠BNE=90°+90°﹣65°=115°,
∵∠NMF=∠AMD,∠MNF=∠BNE,
∴∠NMF+∠MNF=115°,
∴∠F=180°﹣(∠NMF+∠MNF)=180°﹣115°=65°.
14.解:∵AD=BD,
∴∠BAD=∠ABC=40°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADC=∠ABC+∠BAD=40°+40°=80°,∠ADE=∠ADB=180°﹣∠ABC﹣∠BAD=180°﹣40°﹣40°=100°,
∴∠CDE=100°﹣80°=20°,
即∠CDE的度数为20°.
15.解:(1)△ABC的面积=4×5﹣×1×5﹣×1×3﹣×4×4=8;
(2)如图,△A′B′C′即为所求;
(3)如图,点D即为所求.
16.解:(1)∵∠C=90°,
∴∠CAB+∠B=90°,即α+∠NAB+∠B=90°,
∵点A,B关于直线MN对称,
∴∠NAB=∠B,
∴α+2∠B=90°;
故答案为:α+2∠B=90°;
(2)∵△ABC的周长为24,
∴AC+BC+AB=24,
∵,,
∴,
解得AC=6,
∴BC=8,AB=10,
∵点A,B关于直线MN对称,
∴AN=BN,
∴△ACN的周长
=AC+CN+AN
=AC+CN+BN
=AC+BC
=6+8=14.
17.解:(1)①∵点C和点P关于OA对称,
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD
=∠AOC+∠AOP+∠BOP+∠BOD
=2(∠AOP+∠BOP)
=2∠AOB
=2×60°
=120°;
②∵点C和点P关于OA对称,
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COP
=∠AOC+∠AOP+∠BOP+∠BOD
=2(∠AOP+∠BOP)
=2∠AOB
=2n°,
故答案为:2n;
(2)∵点C和点P关于OA对称,
∴CM=PM,
∵点P关于OB对称点是D,
∴DN=PN,
∵CD=4,
∴CM+MN+DN=4,
∴PM+MN+PN=4,
即△PMN的周长为4,
故答案为:4.
18.解:如图.
19.(1)证明:∵∠AFP=60°,∠BFQ=60°,
∴∠AFB=60°,
∴∠AFE=∠AFB,
∵∠BEQ=30°,
∴∠EBF=30°,
∴∠BEQ=∠EBF,
∴FE=FB,
在△FEA和△FBA中,
,
∴△FEA≌△FBA(SAS),
∴AE=AB;
(2)解:∵∠AEP=74°,∠BEQ=30°,
∴∠AEB=76°,
∵AE=AB,
∴∠ABE=∠AEB=76°,
∴∠BAE=28°.
20.解:(1)如图1中,
∠DBC+∠ECB
=180°﹣∠ABC+180°﹣∠ACB
=360°﹣(∠ABC+∠ACB)
=360°﹣(180°﹣∠A)
=180°+∠A;
(2)如图2中,
∵∠1+∠2=∠180°+∠C,
∴130°+∠2=180°+∠C,
∴∠2﹣∠C=50°.
故答案为:50°;
(3)如图3中,
∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°﹣∠A),
在△PBC中,∠P=180°﹣(180°﹣∠A)=90°﹣∠A.
1.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
2.如图,在Rt△ABC中,∠ACB=90°,D是AB边的中点,DE⊥AC,垂足为点E,连接DC.
(1)若∠A=36°,求∠BCD的度数;
(2)若∠A=30°,DE+BC=6,求DE和EC的长.
3.如图,已知△ABC,AD是∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.
(1)求证:AD垂直平分EF;
(2)若AB+AC=10,DE=3,求△ABC的面积.
4.如图,△ABC和△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)图中点C的对应点是点 ,∠B的对应角是 ;
(2)若DE=5,BF=2,则CF的长为 ;
(3)若∠BAC=108°,∠BAE=30°,求∠EAF的度数.
5.如图,直线EF分别交直线AB、CD于点E、F,EP平分∠AEF交CD于点P,点N是射线PC上一点,延长EP到点M,使得PM=PN,连接MN.
(1)若AB∥CD,∠EFD=80°,求∠AEP的度数;
(2)若∠PMN=72.5°,∠AEF=70°,判断直线AB与CD是否平行?并说明理由.
6.如图,在四边形ABCD中,DE垂直平分AB,DF垂直平分BC,垂足分别为E,F.
(1)试说明DA=DC;
(2)如果∠A=70°,∠C=60°,求∠ADC的度数.
7.如图,在△ABC中,AD平分∠BAC,过点B作AD的垂线,垂足为点D,DE∥AC,交AB于点E,CD∥AB.
(1)求证:△BDE是等腰三角形;
(2)求证:CD=BE.
8.如图1,已知直线AB∥CD,点E、F分别在直线AB、CD上,G点为射线FD上一动点,且∠FEG>∠EFG,将△EFG沿着EF翻折得到△EFH,直线EQ平分∠BEH交直线CD于点P.
(1)当EG⊥CD时,
①若∠EFG=30°,则∠PEF= .
②若去掉条件“∠EFG=30°”,你还能求出∠PEF的度数吗?试一试.
(2)如图2,在点G运动的过程中,当∠EGF=a时,求∠PEF的度数(用含a的代数式表示);
(3)在点G运动的过程中,若∠PEG=5°,且∠EGF=4∠EFG,直接写出∠EGF的度数.
9.如图,在△ABC中,AB=AC,∠BAC=40°,AD是BC边上的高.线段AC的垂直平分线交AD于点E,交AC于点F,连接BE.
(1)填空:∠BAD的度数为 ;∠ABC的度数为 ;∠ACB的度数为 .
(2)试问:线段AE与BE的长相等吗?请说明理由;
(3)求∠EBD的度数.
10.如图,点D在等边△ABC的外部,连接AD、CD,AD=CD,过点D作DE∥AB交AC于点F,交BC于点E.
(1)判断△CEF的形状,并说明理由;
(2)连接BD,若BC=10,CF=4,求DE的长.
11.如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
12.如图,在△ABC中,O为∠ABC,∠ACB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F.
(1)OD与OE是否相等.请说明理由;
(2)若△ABC的周长是30,且OF=3,求△ABC的面积.
13.如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为18m,求AB的长;
(2)若∠NCM=50°,求∠F的度数.
14.如图,在△ABC中,点D是BC上的点,AD=BD,将△ABD沿AD翻折得到
△AED,若∠B=40°,求∠CDE的度数.
15.在图示的正方形网格纸中,每个小正方形的边长都是1,△ABC的三个顶点都在小正方形的顶点处,直线MN与网格中竖直的线相重合.
(1)直接写出△ABC的面积;
(2)作出△ABC关于直线MN对称的△A'B'C';
(3)在网格内找一点D,使点D到线段BC,B'C'的距离相等且DB=DC.(在网格上直接标出点D的位置,不写作法)
16.如图,在△ABC中,∠C=90°,点M,N分别在边AB,BC上,且点A,B关于直线MN对称,连接AN.
(1)若∠CAN=α,则∠B与α之间的数最关系为 ;
(2)若,,且△ABC的周长为24.求△ACN的周长.
17.如图,点P在∠AOB的内部,点C和点P关于OA对称,点P关于OB的对称点是点D,连结CD交OA于点M,交OB于点N.
(1)①若∠AOB=60°,求∠COD的度数.
②若∠AOB=n°,则∠COD= °(用含n的代数式表示).
(2)若CD=4,则△PMN的周长为 .
18.如图,由4个小正方形组成的田字格,△ABC的顶点都是小正方形的顶点,请在下列三个田字格中分别画出与△ABC成轴对称,且顶点都在小正方形顶点上的三角形(要求三个图互不相同).
19.如图,大海中有两个岛屿A与B,∠BEQ=30°,在海岸线PQ上的点F处测得∠AFP=60°,∠BFQ=60°.
(1)求证:AE=AB;
(2)若在海岸线PQ上的点E处测得∠AEP=74°,求∠BAE的度数.
20.旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和,那么,三角形的一个内角与它不相部的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系(直接写出结论).
参考答案
1.(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CEF=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=(180°﹣50°)=65°,
∴∠DEF=65°.
2.解:(1)∵∠ACB=90°,D是AB边的中点,
∴AD=CD=BD,
∴∠A=∠DCA=36°,
∴∠BCD=90°﹣36°=54°.
(2)由(1)得,∠A=∠DCA=30°,
∵DE⊥AC,
∴∠DEC=90°,
∴DE=,
∵∠A=30°,∠ACB=90°,
∴∠B=60°,
∴△DCB是等边三角形,
∴CD=BC=2DE,
又∵DE+BC=6,
∴DE=2,BC=DC=4,
∴EC=.
3.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠DEA=∠DFA=90°,
∵AD是∠BAC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD是∠BAC的角平分线,
∴AG⊥EF,EG=FG,
∴AD垂直平分EF;
(2)解:∵AD是∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵DE=3,
∴DF=3,
∵AB+AC=10,
∴△ABC的面积=
==15.
4.解:(1)∵△ABC与△ADE关于直线MN对称,
∴图中点C的对应点是点E,∠B的对应角是∠D;
故答案为:E,∠D.
(2)∵△ABC与△ADE关于直线MN对称,
∴△ABC≌△ADE,
∴BC=DE=5,
∴CF=BC﹣BF=3.
故答案为:3.
(3)∵∠BAC=108°,∠BAE=30°,
∴∠CAE=108°﹣30°=78°,
再根据对称性,
∴∠EAF=∠CAF,
∴∠EAF==39°.
5.解:(1)∵AB∥CD,∠EFD=80°,
∴∠AEF=∠EFD=80°,
∵EP平分∠AEF,
∴∠AEP=∠AEF=40°;
(2)AB∥CD,
理由:∵PN=PM,∠PMN=72.5°,
∴∠PNM=∠PMN=72.5°,
∴∠MPN=35°,
∴∠EPF=∠MPN=35°,
∵EM平分∠AEF,∠AEF=70°,
∴∠AEM=∠AEF=35°,
∴∠AEM=∠EPF,
∴AB∥CD.
6.解:(1)如图,连接DB,
∵DE垂直平分AB,DF垂直平分BC,
∴DA=DB,DC=DB,
∴DA=DC;
(2)∵DA=DB,∠A=70°,
∴∠DBA=∠A=70°,
∵DC=DB,∠C=60°,
∴∠DBC=∠C=60°,
∴∠ABC=∠DBA+∠DBC=130°,
∵∠A+∠ABC+∠C+∠ADC=360°,
∴∠ADC=100°.
7.证明:(1)∵DE∥AC,∠1=∠2,
∴∠1=∠2=∠3=∠4,
∵∠2+∠ABD=90°,∠5+∠4=90°,
∴∠5=∠ABD,
∴DE=BE,
∴△BDE是等腰三角形;
(2)由(1)知,∠4=∠2,
∴AE=DE,
∵AD=AD,∠1=∠4,∠2=∠3,
∴△ACD≌△AED(ASA),
∴CD=AE,
∴CD=AE=DE=BE.
8.解:(1)当EG⊥CD时,∠EGF=90°,
①若∠EFG=30°,则∠FEG=60°,
由翻折可知:∠FEH=CFEG=60°,
∵AB∥CD,
∴∠AEF=∠EFG=30°,
∴∠AEH=∠FEH﹣∠AEF=30°,
∴∠BEH=180°﹣∠AEH=150°,
∵EQ平分∠BEH,
∴∠BEQ=∠BEH=75°,
∴∠AEP=∠BEQ=75°,
∴∠PEF=∠AEP﹣∠AEF=45°,
故答案为:45°;
②若去掉条件“∠EFG=30°“,还能求出∠PEF的度数,
∵∠EGF=90°,
∴∠EFG+∠FEG=90°,
由翻折可知:∠FEH=∠FEG,
∵AB//CD,
∴∠AEF=∠EFG,
∴∠AEH=∠FEH﹣∠AEF=∠FEG﹣∠EFG,
∴∠BEH=180°﹣∠AEH=180°﹣∠FEG+∠EFG,
∵EQ平分∠BEH,
∴∠BEQ=∠BEH=90°﹣∠FEG+∠EFG,
∴∠AEP=∠BEQ=90°﹣∠FEG+∠EFG,
∴∠PEF=∠AEP﹣∠AEF=90°﹣∠FEG+∠EFG﹣∠EFG
=90°﹣∠FEG﹣∠EFG
=90°﹣(∠FEG+∠EFG)
=90°﹣45°
=45°;
(2)在点G运动的过程中,当∠EGF=a时,
∠EFG+∠FEG=180°﹣a,
由翻折可知:∠FEH=∠FEG,
∵AB∥CD,
∴∠AEF=∠EFG,
∴∠AEH=∠FEH﹣∠AEF=CFEG﹣∠EFG,
∴∠BEH=180°﹣∠AEH=180°﹣∠FEG+∠EFG,
∵EQ平分∠BEH,
∴∠BEQ=∠BEH=90°﹣∠FEG+∠EFG,
∴∠AEP=∠BEQ=90°﹣∠FEG+∠EFG,
∴∠PEF=∠AEP﹣∠AEF=90°﹣∠FEG+∠EFG﹣∠EFG
=90°﹣∠FEG﹣∠EFG
=90°﹣(∠FEG+∠EFG)
=90°﹣(180°﹣a)
=a,
即∠PEF的度数为α;
(3)由(2)知:在点G运动的过程中,
∠PEF=∠EGF,
在点G运动的过程中,若∠PEG=5°,且∠EGF=4∠EFG,
则∠EFG=∠EGF,
点G在点P的右侧时,
∠FEG=∠PEF+∠PEG=∠EGF+5°
∵∠EGF+∠EFG+∠FEG=180°,
∴∠EGF+∠EGF+∠EGF﹣5°=180°
解得:∠EGF=,
综上所述,∠EGF的度数为100°或.
9.解:(1)∵AB=AC,∠BAC=40°,AD是BC边上的高,
∴∠BAD=∠CAD=∠BAC=20°,∠ACB=∠ABC=(180°﹣∠BAC)=×(180°﹣40°)=70°,
故答案为:20°,70°,70°;
(2)线段AE与BE的长相等,理由如下:
如图,连接CE,
∵AB=AC,AD是BC边上的高,
∴BD=CD,AD⊥BC,
∴BE=CE,
∵EF是线段AC的垂直平分线,
∴AE=CE,
∴AE=BE;
(3)由(2)可知,∠ABC=70°,AE=BE,
∴∠ABE=∠BAD=20°,
∴∠EBD=∠ABC﹣∠ABE=70°﹣20°=50°.
10.解:(1)△CEF是等边三角形,理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵AB∥DE,
∴∠CEF=∠ABC=60°,
∴∠CEF=∠CFE=∠ECF=60°,
∴△CEF是等边三角形;
(2)∵△ABC是等边三角形,△CEF是等边三角形,
∴AB=BC,CF=CE=4.
∵AD=CD,
∴BD是线段AC的垂直平分线,
∴BD平分∠ABC,
∴∠ABD=∠CBD.
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠BDE=∠CBD,
∴BE=DE.
∵BC=BE+EC=DE+CF,
∴DE=BC﹣CF=10﹣4=6.
11.(1)解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=ABC,,
∴∠CBE+∠BCF=∠ABC+ACB==60°,
∴∠BPC=180°﹣(∠CBE+∠BCF)=180°﹣60°=120°;
(2)证明:在BC上截取BQ=BF,连接PQ,
在△FBP和△QBP中,
,
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°﹣60°﹣120°=180°,
∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP,
在△CQP和△CEP中,
,
∴△CQP≌△CEP(AAS),
∴EF=QP,
∵FP=EP,
∴△EFP是等腰三角形.
12.解:(1)OD=OE,
理由:∵O为∠ABC,∠ACB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,
∴OD=OF,OF=OE,
∴OD=OE;
(2)连接OA,
∴△ABC的面积=S△AOB+S△BOC+S△AOC=AB OD+BC OF+AC OE,
∵OE=OD=OF,
∴△ABC的面积=(AB+BC+AC) OF=×30×3=45.
13.(1)解:∵DM、EN分别垂直平分AC和BC,
∴MA=MC,BN=CN,
∵△CMN的周长为18m,
∴CM+MN+CN=18m,
∴AB=AM+MN+BN=CM+MN+CN=18m;
(2)解:∵DM、EN分别垂直平分AC和BC,
∴MA=MC,BN=CN,
∴∠MCA=∠A,∠NCB=∠B,
∵∠A+∠B+∠ACB=∠A+∠B+∠NCB+∠NCM+∠MCA=180°,
∴2∠A+2∠B+∠NCM=180°,
即2∠A+2∠B+50°=180°,
∴∠A+∠B=65°,
∵DM⊥AC,EN⊥BC,
∴∠A+∠AMD=90°,∠B+∠BNE=90°,
∴∠AMD+∠BNE=90°+90°﹣65°=115°,
∵∠NMF=∠AMD,∠MNF=∠BNE,
∴∠NMF+∠MNF=115°,
∴∠F=180°﹣(∠NMF+∠MNF)=180°﹣115°=65°.
14.解:∵AD=BD,
∴∠BAD=∠ABC=40°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADC=∠ABC+∠BAD=40°+40°=80°,∠ADE=∠ADB=180°﹣∠ABC﹣∠BAD=180°﹣40°﹣40°=100°,
∴∠CDE=100°﹣80°=20°,
即∠CDE的度数为20°.
15.解:(1)△ABC的面积=4×5﹣×1×5﹣×1×3﹣×4×4=8;
(2)如图,△A′B′C′即为所求;
(3)如图,点D即为所求.
16.解:(1)∵∠C=90°,
∴∠CAB+∠B=90°,即α+∠NAB+∠B=90°,
∵点A,B关于直线MN对称,
∴∠NAB=∠B,
∴α+2∠B=90°;
故答案为:α+2∠B=90°;
(2)∵△ABC的周长为24,
∴AC+BC+AB=24,
∵,,
∴,
解得AC=6,
∴BC=8,AB=10,
∵点A,B关于直线MN对称,
∴AN=BN,
∴△ACN的周长
=AC+CN+AN
=AC+CN+BN
=AC+BC
=6+8=14.
17.解:(1)①∵点C和点P关于OA对称,
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COD
=∠AOC+∠AOP+∠BOP+∠BOD
=2(∠AOP+∠BOP)
=2∠AOB
=2×60°
=120°;
②∵点C和点P关于OA对称,
∴∠AOC=∠AOP,
∵点P关于OB对称点是D,
∴∠BOD=∠BOP,
∴∠COP
=∠AOC+∠AOP+∠BOP+∠BOD
=2(∠AOP+∠BOP)
=2∠AOB
=2n°,
故答案为:2n;
(2)∵点C和点P关于OA对称,
∴CM=PM,
∵点P关于OB对称点是D,
∴DN=PN,
∵CD=4,
∴CM+MN+DN=4,
∴PM+MN+PN=4,
即△PMN的周长为4,
故答案为:4.
18.解:如图.
19.(1)证明:∵∠AFP=60°,∠BFQ=60°,
∴∠AFB=60°,
∴∠AFE=∠AFB,
∵∠BEQ=30°,
∴∠EBF=30°,
∴∠BEQ=∠EBF,
∴FE=FB,
在△FEA和△FBA中,
,
∴△FEA≌△FBA(SAS),
∴AE=AB;
(2)解:∵∠AEP=74°,∠BEQ=30°,
∴∠AEB=76°,
∵AE=AB,
∴∠ABE=∠AEB=76°,
∴∠BAE=28°.
20.解:(1)如图1中,
∠DBC+∠ECB
=180°﹣∠ABC+180°﹣∠ACB
=360°﹣(∠ABC+∠ACB)
=360°﹣(180°﹣∠A)
=180°+∠A;
(2)如图2中,
∵∠1+∠2=∠180°+∠C,
∴130°+∠2=180°+∠C,
∴∠2﹣∠C=50°.
故答案为:50°;
(3)如图3中,
∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°﹣∠A),
在△PBC中,∠P=180°﹣(180°﹣∠A)=90°﹣∠A.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
