2022—2023学年北师大版八年级数学下册 第六章 平行四边形中点之倍长中线 专项练习(Word版,含解析)
文档属性
| 名称 | 2022—2023学年北师大版八年级数学下册 第六章 平行四边形中点之倍长中线 专项练习(Word版,含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 736.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览



文档简介
北师版八年级下册第六单元平行四边形中点之倍长中线专项练习
中点中线可倍长,8字全等来帮忙
定 义 示例剖析
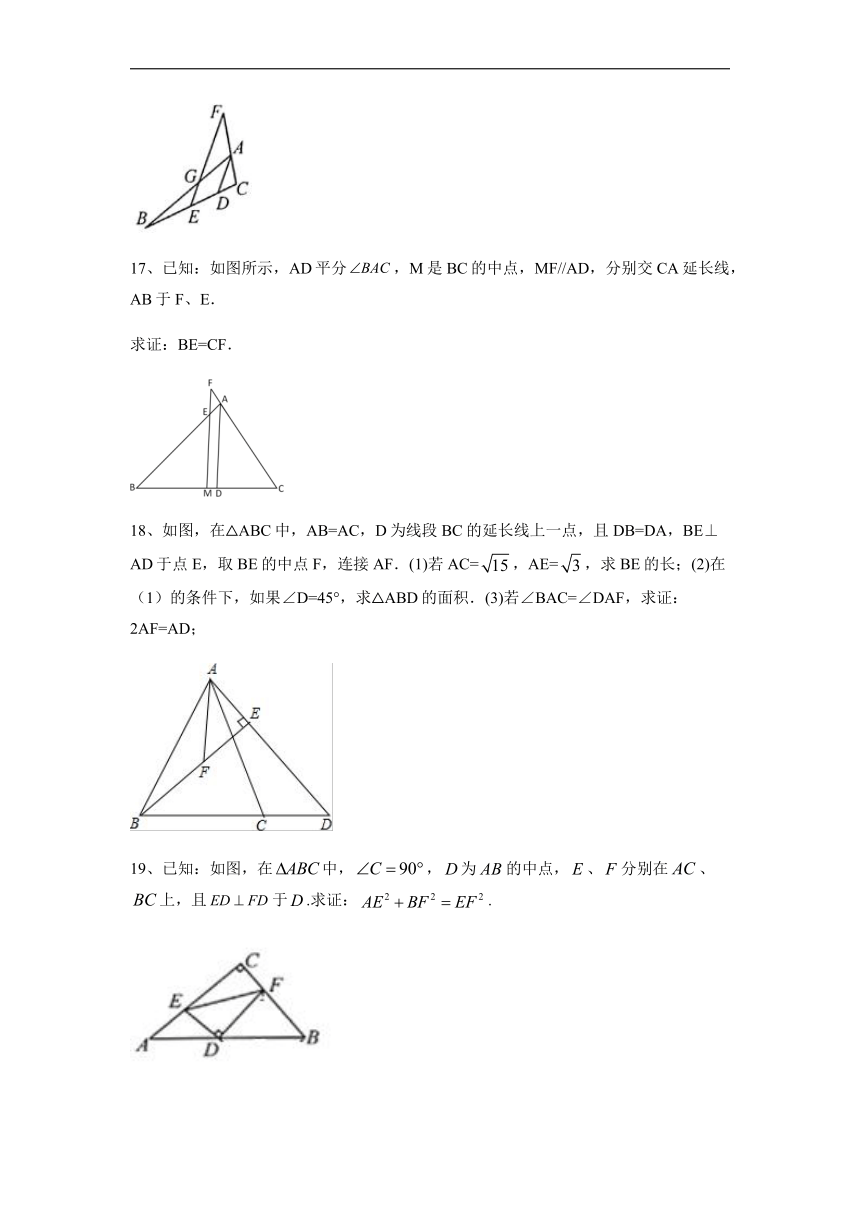
一、例题讲解
1、已知,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
2、已知,如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC. 求证:AE平分
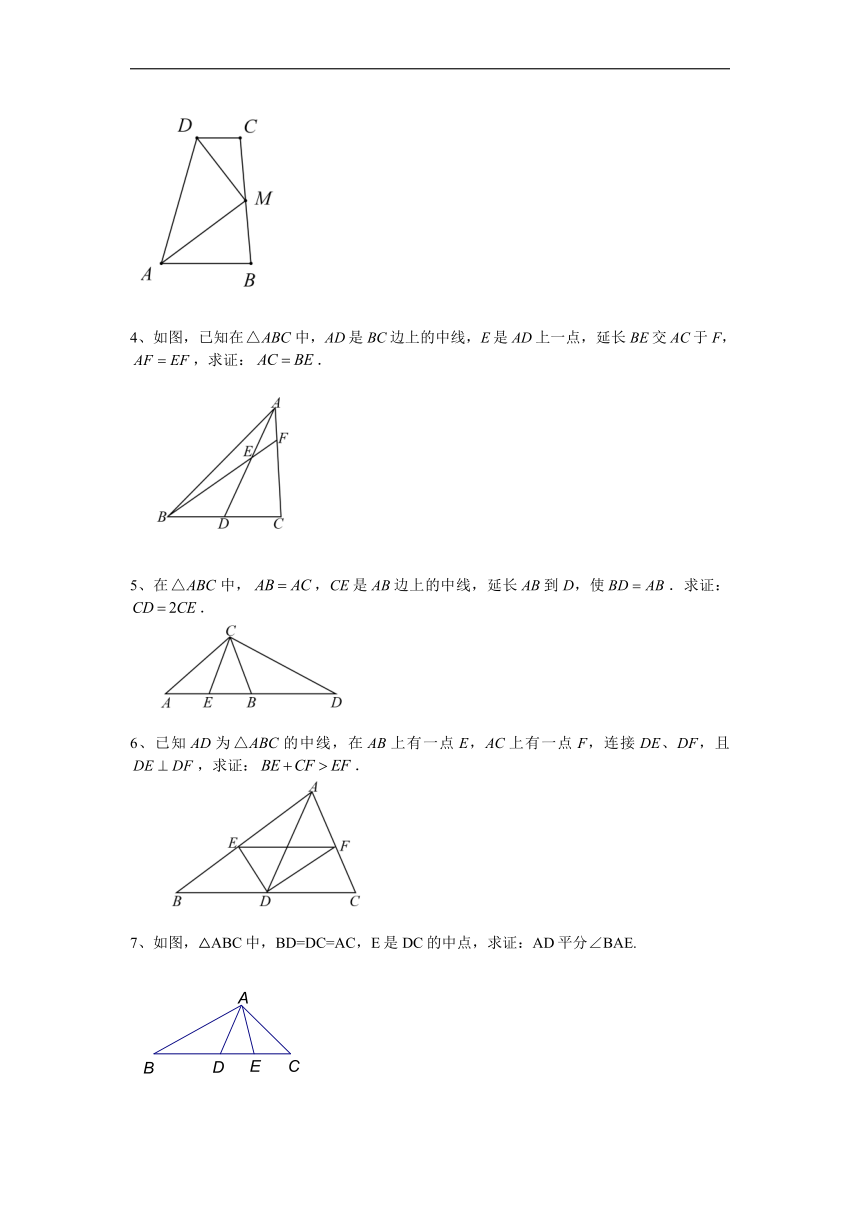
3、如图,AB∥CD,M是BC的中点,DM平分∠ADC,DM⊥AM。求证:AM平分∠DAB。
4、如图,已知在中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,,求证:.
5、在中,,CE是AB边上的中线,延长AB到D,使.求证:.
6、已知AD为的中线,在AB上有一点E,AC上有一点F,连接DE、DF,且,求证:.
7、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
经典例题
8、⑴如图,已知中,,是边上的中线,延长到,使.给出下列结论:①AD=2AC;②CD=2CE;③∠ACE=∠BCD;④CB平分∠DCE,则以上结论正确的是 .
9、⑵如图,在△ABC中,点D、E为边BC的三等分点,给出下列结论:①BD=DE=EC;②AB+AE>2AD;③AD+AC>2AE;④AB+AC>AD+AE,则以上结论正确的是 .
10、如图,平行四边形中,于,点为边中点,,,则_________
11、如图,为AD上的中点,则BE=______.
12、已知为的中线,、的平分线分别交于、交于.求证:.
13、如图,已知在中,是边上的中线,是上一点,延长交于,,求证:.
14、如图所示,在中,为中线,,求的度数.
15、已知:如图所示,在中,为中线,交分别于,如果,求证: .
16、如图所示,在中,交于点,点是中点,交的延长线于点,交于点,若,求证:为的平分线.
17、已知:如图所示,AD平分,M是BC的中点,MF//AD,分别交CA延长线,AB于F、E.
求证:BE=CF.
18、如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.(1)若AC=,AE=,求BE的长;(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.(3)若∠BAC=∠DAF,求证:2AF=AD;
19、已知:如图,在中,,为的中点,、分别在、上,且于.求证:.
答案解析
一、例题讲解
1、已知,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
解析:延长中线AD到点G,使得DG=AD,联结BG,可证 DBG≌ DCA(SAS),得到BG=AC,∠G=∠CAD,因为BE=AC,所以BE=BG,从而得等腰三角形BEG,利用角的等量代换,得到∠FAE=∠AEF从而得证。
2、已知,如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC. 求证:AE平分
解析:延长中线AE到点G,使得GE=AE,联结DG,可证 DEG≌ CEA(SAS),得到DG=AC,∠G=∠CAE,因为DF=AC,所以DF=DG,从而得等腰三角形DGF,利用角的等量代换,得到∠CAE=∠BAE从而得证。
3、如图,AB∥CD,M是BC的中点,DM平分∠ADC,DM⊥AM。求证:AM平分∠DAB。
证明:延长DM和AB交于点N,证明△DCM≌△BNM(ASA或AAS),得到DM=MN再证明△ADM≌△ANM(SAS)
4、如图,已知在中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,,求证:.
延长AD到G,使,连接BG.∵,,,∴,∴.,又∵,∴,∴,∴,∴.
5、在中,,CE是AB边上的中线,延长AB到D,使.求证:.
延长CE到F,使,连接BF.∵CE是AB的中线,∴. 在和中
,∴,∴,∴
在和中,∴,∴.
6、已知AD为的中线,在AB上有一点E,AC上有一点F,连接DE、DF,且,求证:.
延长FD到N,使,连接BN、EN.易证,∴,又∵,利用SAS证明,∴,在中,,∴.
7、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
解:延长AE至G使AG=2AE,连BG,DG,显然DG=AC, ∠GDC=∠ACD
由于DC=AC,故 ∠ADC=∠DAC在△ADB与△ADG中,BD=AC=DG,AD=AD,
∠ADB=∠ADC+∠ACD=∠ADC+∠GDC=∠ADG故△ADB≌△ADG,故有∠BAD=∠DAG,即AD平分∠BAE
经典例题
8、⑴如图,已知中,,是边上的中线,延长到,使.给出下列结论:①AD=2AC;②CD=2CE;③∠ACE=∠BCD;④CB平分∠DCE,则以上结论正确的是 .
①正确.∵,,∴AD=2AC.②、④正确.延长到,使,连接.∵是的中线,∴.在和中
∴∴,
∴
在和中
∴∴,∠FCB=∠DCB即CD=2CE,CB平分∠DCE.
③错误.∵∠FCB=∠DCB,而CE是AB边上中线而不是∠ACB的角平分线故∠ACE和∠BCD不一定相等.
9、⑵如图,在△ABC中,点D、E为边BC的三等分点,给出下列结论:①BD=DE=EC;②AB+AE>2AD;③AD+AC>2AE;④AB+AC>AD+AE,则以上结论正确的是 .
点D、E为边BC的三等分点,∴BD=DE=CE延长AD至点M,AE至点N,使得DM=AD,EN=AE,连接EM、CN,则可证明△ABD≌△MED,进而可得AB+AE>2AD,再证明△ADE≌△NCE,进而可得AD+AC>2AE,将两式相加可得到AB+AE+AD+AC>2AD+2AE,即AB+AC>AD+AE.∴①②③④均正确.
10、如图,平行四边形中,于,点为边中点,,,则_________
解:延长、交于点,连接FC,∵平行四边形中,∴,,,
∴,,,又∵点为边中点,得,
∴≌(ASA),,∴,∴,
∴,∴,∵,,,,∴,∴,∴,
∴,故答案为:.
11、如图,为AD上的中点,则BE=______.
解:延长BE交CD于点F,∵AB平行CD,则∠A=∠EDC,∠ABE=∠DFE,
又E为AD上的中点,∴BE=EF,所以.∴
∴在直角三角形BCF中,BF==.∴.
12、已知为的中线,、的平分线分别交于、交于.求证:.
延长到,使,连接、.易证,∴,
又∵、的平分线分别交于、交于,∴,
利用证明,∴,在中,,∴.
13、如图,已知在中,是边上的中线,是上一点,延长交于,,求证:.
解:延长到,使,连接∵,,∴,∴,又∵,∴∴,∴,∴.
14、如图所示,在中,为中线,,求的度数.
解:延长AD至E,使,连结,∵BD=CD,∠ADB=∠EDC∴,∴EC=AB,,∵AB=2AD,∴AB=AE=EC∴△AEC是等腰直角三角形,∴∠DAC=45°.故答案为45°.
15、已知:如图所示,在中,为中线,交分别于,如果,求证: .
解证明:延长ED至G,使,连结GC, ∵在中,为中线,∴BD=CD,
在△ADC和△GDB中, ∴,,,
,,.又,∴,
∴.
16、如图所示,在中,交于点,点是中点,交的延长线于点,交于点,若,求证:为的平分线.
解证明:延长FE,截取EH=EG,连接CH,∵E是BC中点,∴BE=CE,∴∠BEG=∠CEH,在△BEG和△CEH中,,∴△BEG≌△CEH(SAS),∴∠BGE=∠H,∴∠BGE=∠FGA=∠H,
∴BG=CH,∵CF=BG,∴CH=CF,∴∠F=∠H=∠FGA,∵EF∥AD,∴∠F=∠CAD,∠BAD=∠FGA,
∴∠CAD=∠BAD,∴AD平分∠BAC.
17、已知:如图所示,AD平分,M是BC的中点,MF//AD,分别交CA延长线,AB于F、E.
求证:BE=CF.
解证明:过B作BN∥AC交EM延长线于N点,∵BN∥AC,BM=CM,∴∠BMN=∠CMF,∠N=∠F,
∴△BMN≌△CMF,∴CF=BN,又∵MF//AD,AD平分∠BAC,∴∠F=∠DAC=∠BAD=∠BEM,
∴∠BEM=∠N,∴BE=BN=CF.
18、如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.(1)若AC=,AE=,求BE的长;(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.(3)若∠BAC=∠DAF,求证:2AF=AD;
解(1)解:∵AB=AC,AC=,∴AB=,∵BE⊥AD,AE=,
∴在Rt△AEB中,;
(2)解:∵BE⊥AD,∠D=45°,∴∠EBD=∠D =45°,∴BE=DE=,
∴AD=AE+DE=,∴;
(3)证明:如图,延长AF至M点,使AF=MF,连接BM,
∵点F为BE的中点,∴EF=BF,在△AEF和△MBF中,
∴△AEF≌△MBF(SAS),∴∠FAE=∠FMB,∴AE∥MB,∴∠EAB+∠ABM=180°,∴∠ABM=180°﹣∠BAD,
又∵AB=AC,DB=DA,∴∠ABC=∠ACB=∠BAD,∴∠ACD=180°﹣∠ACB,
∴∠ABM=∠ACD.又∵∠BAC=∠DAF,∴∠BAC﹣∠MAC=∠DAF﹣∠MAC,∴∠1=∠2.
在△ABM和△ACD中,,∴△ABM≌△ACD(ASA),∴AM=AD,
又∵AM=AF+MF=2AF,∴2AF=AD.
19、已知:如图,在中,,为的中点,、分别在、上,且于.求证:.
解延长至,使,连结、,,,,
,,,,,
,又,,,.
中点中线可倍长,8字全等来帮忙
定 义 示例剖析
一、例题讲解
1、已知,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
2、已知,如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC. 求证:AE平分
3、如图,AB∥CD,M是BC的中点,DM平分∠ADC,DM⊥AM。求证:AM平分∠DAB。
4、如图,已知在中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,,求证:.
5、在中,,CE是AB边上的中线,延长AB到D,使.求证:.
6、已知AD为的中线,在AB上有一点E,AC上有一点F,连接DE、DF,且,求证:.
7、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
经典例题
8、⑴如图,已知中,,是边上的中线,延长到,使.给出下列结论:①AD=2AC;②CD=2CE;③∠ACE=∠BCD;④CB平分∠DCE,则以上结论正确的是 .
9、⑵如图,在△ABC中,点D、E为边BC的三等分点,给出下列结论:①BD=DE=EC;②AB+AE>2AD;③AD+AC>2AE;④AB+AC>AD+AE,则以上结论正确的是 .
10、如图,平行四边形中,于,点为边中点,,,则_________
11、如图,为AD上的中点,则BE=______.
12、已知为的中线,、的平分线分别交于、交于.求证:.
13、如图,已知在中,是边上的中线,是上一点,延长交于,,求证:.
14、如图所示,在中,为中线,,求的度数.
15、已知:如图所示,在中,为中线,交分别于,如果,求证: .
16、如图所示,在中,交于点,点是中点,交的延长线于点,交于点,若,求证:为的平分线.
17、已知:如图所示,AD平分,M是BC的中点,MF//AD,分别交CA延长线,AB于F、E.
求证:BE=CF.
18、如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.(1)若AC=,AE=,求BE的长;(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.(3)若∠BAC=∠DAF,求证:2AF=AD;
19、已知:如图,在中,,为的中点,、分别在、上,且于.求证:.
答案解析
一、例题讲解
1、已知,在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
解析:延长中线AD到点G,使得DG=AD,联结BG,可证 DBG≌ DCA(SAS),得到BG=AC,∠G=∠CAD,因为BE=AC,所以BE=BG,从而得等腰三角形BEG,利用角的等量代换,得到∠FAE=∠AEF从而得证。
2、已知,如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC. 求证:AE平分
解析:延长中线AE到点G,使得GE=AE,联结DG,可证 DEG≌ CEA(SAS),得到DG=AC,∠G=∠CAE,因为DF=AC,所以DF=DG,从而得等腰三角形DGF,利用角的等量代换,得到∠CAE=∠BAE从而得证。
3、如图,AB∥CD,M是BC的中点,DM平分∠ADC,DM⊥AM。求证:AM平分∠DAB。
证明:延长DM和AB交于点N,证明△DCM≌△BNM(ASA或AAS),得到DM=MN再证明△ADM≌△ANM(SAS)
4、如图,已知在中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,,求证:.
延长AD到G,使,连接BG.∵,,,∴,∴.,又∵,∴,∴,∴,∴.
5、在中,,CE是AB边上的中线,延长AB到D,使.求证:.
延长CE到F,使,连接BF.∵CE是AB的中线,∴. 在和中
,∴,∴,∴
在和中,∴,∴.
6、已知AD为的中线,在AB上有一点E,AC上有一点F,连接DE、DF,且,求证:.
延长FD到N,使,连接BN、EN.易证,∴,又∵,利用SAS证明,∴,在中,,∴.
7、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
解:延长AE至G使AG=2AE,连BG,DG,显然DG=AC, ∠GDC=∠ACD
由于DC=AC,故 ∠ADC=∠DAC在△ADB与△ADG中,BD=AC=DG,AD=AD,
∠ADB=∠ADC+∠ACD=∠ADC+∠GDC=∠ADG故△ADB≌△ADG,故有∠BAD=∠DAG,即AD平分∠BAE
经典例题
8、⑴如图,已知中,,是边上的中线,延长到,使.给出下列结论:①AD=2AC;②CD=2CE;③∠ACE=∠BCD;④CB平分∠DCE,则以上结论正确的是 .
①正确.∵,,∴AD=2AC.②、④正确.延长到,使,连接.∵是的中线,∴.在和中
∴∴,
∴
在和中
∴∴,∠FCB=∠DCB即CD=2CE,CB平分∠DCE.
③错误.∵∠FCB=∠DCB,而CE是AB边上中线而不是∠ACB的角平分线故∠ACE和∠BCD不一定相等.
9、⑵如图,在△ABC中,点D、E为边BC的三等分点,给出下列结论:①BD=DE=EC;②AB+AE>2AD;③AD+AC>2AE;④AB+AC>AD+AE,则以上结论正确的是 .
点D、E为边BC的三等分点,∴BD=DE=CE延长AD至点M,AE至点N,使得DM=AD,EN=AE,连接EM、CN,则可证明△ABD≌△MED,进而可得AB+AE>2AD,再证明△ADE≌△NCE,进而可得AD+AC>2AE,将两式相加可得到AB+AE+AD+AC>2AD+2AE,即AB+AC>AD+AE.∴①②③④均正确.
10、如图,平行四边形中,于,点为边中点,,,则_________
解:延长、交于点,连接FC,∵平行四边形中,∴,,,
∴,,,又∵点为边中点,得,
∴≌(ASA),,∴,∴,
∴,∴,∵,,,,∴,∴,∴,
∴,故答案为:.
11、如图,为AD上的中点,则BE=______.
解:延长BE交CD于点F,∵AB平行CD,则∠A=∠EDC,∠ABE=∠DFE,
又E为AD上的中点,∴BE=EF,所以.∴
∴在直角三角形BCF中,BF==.∴.
12、已知为的中线,、的平分线分别交于、交于.求证:.
延长到,使,连接、.易证,∴,
又∵、的平分线分别交于、交于,∴,
利用证明,∴,在中,,∴.
13、如图,已知在中,是边上的中线,是上一点,延长交于,,求证:.
解:延长到,使,连接∵,,∴,∴,又∵,∴∴,∴,∴.
14、如图所示,在中,为中线,,求的度数.
解:延长AD至E,使,连结,∵BD=CD,∠ADB=∠EDC∴,∴EC=AB,,∵AB=2AD,∴AB=AE=EC∴△AEC是等腰直角三角形,∴∠DAC=45°.故答案为45°.
15、已知:如图所示,在中,为中线,交分别于,如果,求证: .
解证明:延长ED至G,使,连结GC, ∵在中,为中线,∴BD=CD,
在△ADC和△GDB中, ∴,,,
,,.又,∴,
∴.
16、如图所示,在中,交于点,点是中点,交的延长线于点,交于点,若,求证:为的平分线.
解证明:延长FE,截取EH=EG,连接CH,∵E是BC中点,∴BE=CE,∴∠BEG=∠CEH,在△BEG和△CEH中,,∴△BEG≌△CEH(SAS),∴∠BGE=∠H,∴∠BGE=∠FGA=∠H,
∴BG=CH,∵CF=BG,∴CH=CF,∴∠F=∠H=∠FGA,∵EF∥AD,∴∠F=∠CAD,∠BAD=∠FGA,
∴∠CAD=∠BAD,∴AD平分∠BAC.
17、已知:如图所示,AD平分,M是BC的中点,MF//AD,分别交CA延长线,AB于F、E.
求证:BE=CF.
解证明:过B作BN∥AC交EM延长线于N点,∵BN∥AC,BM=CM,∴∠BMN=∠CMF,∠N=∠F,
∴△BMN≌△CMF,∴CF=BN,又∵MF//AD,AD平分∠BAC,∴∠F=∠DAC=∠BAD=∠BEM,
∴∠BEM=∠N,∴BE=BN=CF.
18、如图,在△ABC中,AB=AC,D为线段BC的延长线上一点,且DB=DA,BE⊥AD于点E,取BE的中点F,连接AF.(1)若AC=,AE=,求BE的长;(2)在(1)的条件下,如果∠D=45°,求△ABD的面积.(3)若∠BAC=∠DAF,求证:2AF=AD;
解(1)解:∵AB=AC,AC=,∴AB=,∵BE⊥AD,AE=,
∴在Rt△AEB中,;
(2)解:∵BE⊥AD,∠D=45°,∴∠EBD=∠D =45°,∴BE=DE=,
∴AD=AE+DE=,∴;
(3)证明:如图,延长AF至M点,使AF=MF,连接BM,
∵点F为BE的中点,∴EF=BF,在△AEF和△MBF中,
∴△AEF≌△MBF(SAS),∴∠FAE=∠FMB,∴AE∥MB,∴∠EAB+∠ABM=180°,∴∠ABM=180°﹣∠BAD,
又∵AB=AC,DB=DA,∴∠ABC=∠ACB=∠BAD,∴∠ACD=180°﹣∠ACB,
∴∠ABM=∠ACD.又∵∠BAC=∠DAF,∴∠BAC﹣∠MAC=∠DAF﹣∠MAC,∴∠1=∠2.
在△ABM和△ACD中,,∴△ABM≌△ACD(ASA),∴AM=AD,
又∵AM=AF+MF=2AF,∴2AF=AD.
19、已知:如图,在中,,为的中点,、分别在、上,且于.求证:.
解延长至,使,连结、,,,,
,,,,,
,又,,,.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
