2022—2023学年京改版八年级数学下册 15.4 特殊的平行四边形的性质与判定 同步练习(Word版,含解析)
文档属性
| 名称 | 2022—2023学年京改版八年级数学下册 15.4 特殊的平行四边形的性质与判定 同步练习(Word版,含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 448.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 00:00:00 | ||
图片预览



文档简介
北京课改版八下 15.4 特殊的平行四边形的性质与判定
一、选择题(共8小题)
1. 矩形具有而平行四边形不一定具有的性质是
A. 对边相等 B. 对角相等
C. 对角线相等 D. 对角线互相平分
2. 下列结论中,矩形具有而菱形不一定具有的性质是
A. 内角和为 B. 对角线互相平分
C. 对角线相等 D. 对角线互相垂直
3. 菱形 在平面直角坐标系中的位置如图所示,点 的坐标是 ,点 的纵坐标是 ,则点 的坐标是
A. B. C. D.
4. 正方形具有而菱形不具有的性质是
A. 对角线平分一组对角 B. 对角互补
C. 四边相等 D. 对边平行
5. 如图,在平行四边形 中,, 是 上两点,,连接 ,,,,添加一个条件,使四边形 是矩形,这个条件可以是
A. B.
C. D.
6. 下列说法正确的是
A. 对角线互相垂直的平行四边形是正方形
B. 四角相等的四边形是正方形
C. 四边相等的四边形是正方形
D. 对角线互相垂直平分且相等的四边形是正方形
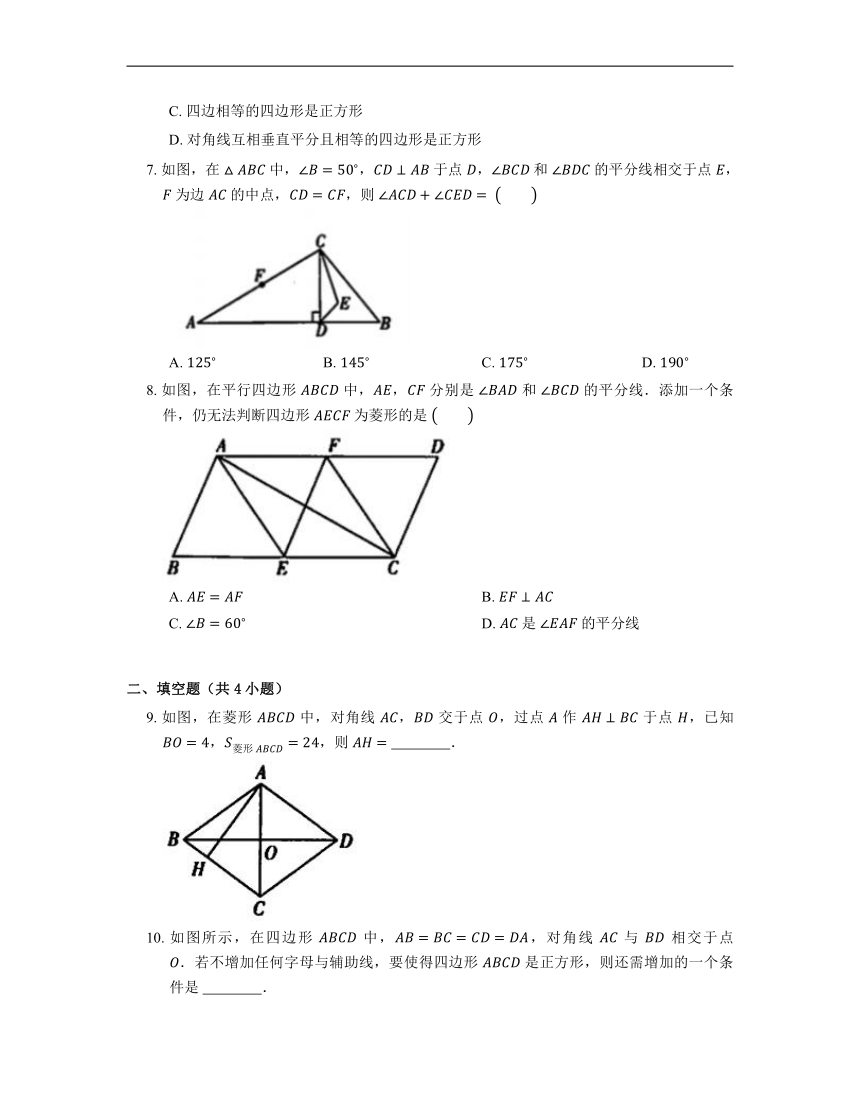
7. 如图,在 中,, 于点 , 和 的平分线相交于点 , 为边 的中点,,则
A. B. C. D.
8. 如图,在平行四边形 中,, 分别是 和 的平分线.添加一个条件,仍无法判断四边形 为菱形的是
A. B.
C. D. 是 的平分线
二、填空题(共4小题)
9. 如图,在菱形 中,对角线 , 交于点 ,过点 作 于点 ,已知 ,,则 .
10. 如图所示,在四边形 中,,对角线 与 相交于点 .若不增加任何字母与辅助线,要使得四边形 是正方形,则还需增加的一个条件是 .
11. 如图,在矩形 中,对角线 与 相交于点 ,过点 作 ,垂足为点 ,若 ,则 度.
12. 如图,四边形 是正方形, 为等边三角形,, 相交于点 ,连接 ,则 .
三、解答题(共6小题)
13. 如图,在平行四边形 中,点 , 是直线 上的两点,.
(1)求证:四边形 是平行四边形.
(2)若 ,,,四边形 是矩形,求 的长.
14. 如图,在四边形 中,, 是 的中点, 平分 交 于点 .
(1)求证:;
(2)猜想 与 具有怎样的位置关系,并证明你的猜想.
15. 如图,四边形 为正方形,,点 是边 上一动点,在点 移动的过程中,始终保证 ,交 于点 ,求证:.
16. 如图,在 中, 是 边上的一点, 是 的中点,过 点作 的平行线交 的延长线于 ,且 ,连接 .
(1)求证: 是 的中点;
(2)如果 ,试判断四边形 的形状,并证明你的结论.
17. 如图,在 中,,点 是 的中点,, 的平分线 交 于点 ,作 ,连接 并延长交 于点 ,连接 .求证:四边形 是菱形.
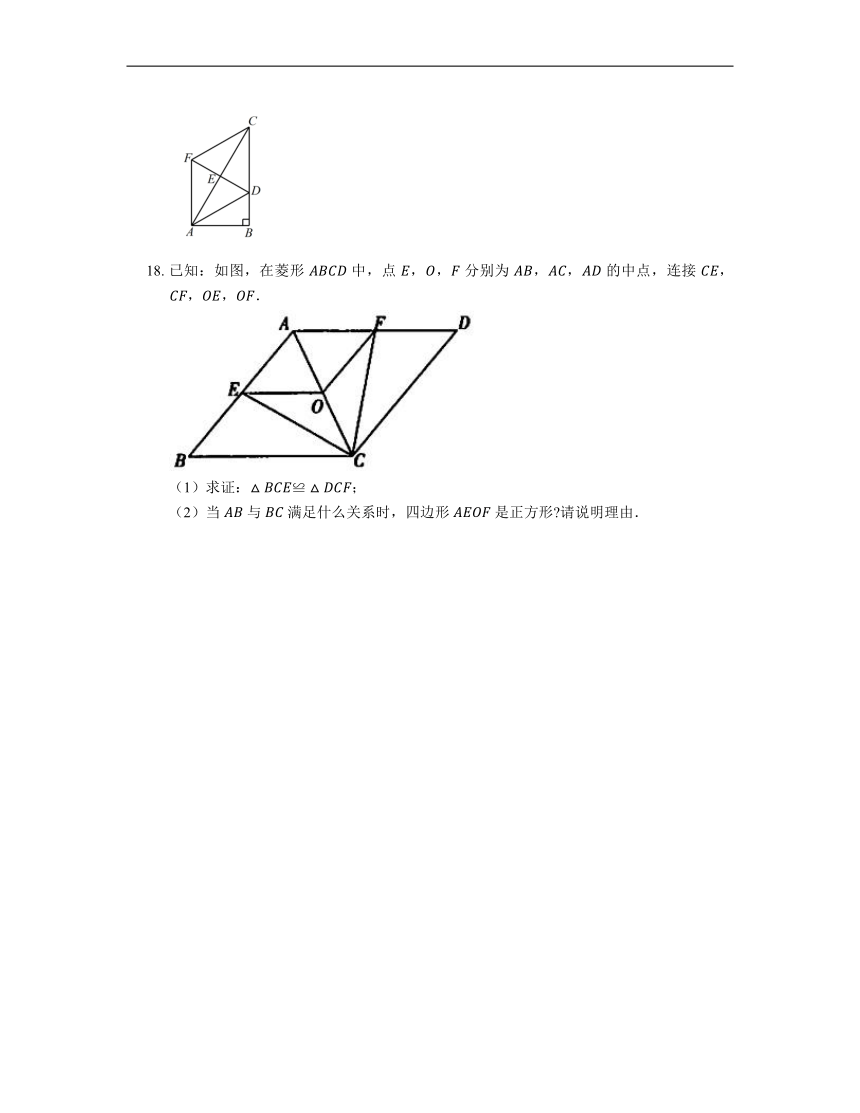
18. 已知:如图,在菱形 中,点 ,, 分别为 ,, 的中点,连接 ,,,.
(1)求证:;
(2)当 与 满足什么关系时,四边形 是正方形 请说明理由.
答案
1. C
【解析】矩形的对角线相等,而平行四边形的对角线不一定相等.
2. C
【解析】矩形和菱形的内角和都为 ,矩形的对角线互相平分且相等,菱形的对角线垂直且平分,
矩形具有而菱形不具有的性质为对角线相等.
3. B
【解析】连接 交 于点 ,
四边形 是菱形,
,,,
点 的坐标是 .
4. B
5. A
【解析】因为四边形 是平行四边形,
所以 ,.
因为 ,
所以 ,即 ,
所以四边形 是平行四边形.
若 ,则 ,
所以四边形 是矩形;
若 ,则不能证明四边形 是矩形;
若 ,则四边形 是菱形;
若 ,则不能证明四边形 是矩形.
6. D
【解析】对角线互相垂直的平行四边形是菱形;
四角相等的四边形是矩形;
四边相等的四边形是菱形;
对角线互相垂直平分且相等的四边形是正方形.
7. C
【解析】连接 ,
, 为边 的中点,
,
又 ,
,
是等边三角形,
,
,
,
和 的平分线相交于点 ,
,
,
,故选C.
8. C
【解析】 四边形 是平行四边形,
,,,.
, 分别是 和 的平分线,
,,
.
在 和 中,
.
,又 ,
,又 ,
四边形 是平行四边形.
A项, 四边形 是平行四边形,,
四边形 是菱形,故本选项不符合要求;
B项,,四边形 是平行四边形,
四边形 是菱形,故本选项不符合要求;
C项,根据 和平行四边形 不能推出四边形 是菱形,故本选项符合要求;
D项, 四边形 是平行四边形,
,
.
平分 ,
,
,
,
四边形 是菱形,故本选项不符合要求.
9.
【解析】 四边形 是菱形,
,,,
,
,
,
,
,
又 ,
.
10. 或 、 、 、 四个角中有一个角是直角.
11.
【解析】 四边形 是矩形,
,,.
,
, ,
,
,
,
,
,
,
,
.
12.
【解析】 四边形 是正方形, 是等边三角形,
,,,,,
,,
,
,
,,,
,
,
,
,
.
13. (1) 四边形 是平行四边形,
,.
.
.
又 ,
.
,.
,
四边形 是平行四边形.
(2) ,,,
,
连接 交 于 ,
,
,
四边形 是矩形,
,,,
,
.
14. (1) , 为 的中点,
为 斜边的中线, 为 斜边的中线,
,,
.
(2) 猜想: 垂直平分 .
证明:, 平分 ,
且 ,
即 垂直平分 .
15. 如图,在 上取一点 ,使 ,连接 .
,即 ,
四边形 为正方形,
,
,
.
,
.
,
,
,
,,
,
,
.
16. (1) ,
,
是 的中点,
.
,
.
,
,
,
是 的中点.
(2) 四边形 是矩形.
证明:,,
四边形 是平行四边形,
, 是 的中点,
,
,
四边形 是矩形.
17. ,
,
在 和 中,
,
,
,
四边形 是平行四边形,
,,
,
平分 ,
,
,
四边形 是菱形.
18. (1) 四边形 是菱形,
,,
点 ,, 分别为 ,, 的中点,
,,,,
在 和 中,
.
(2) 当 时,四边形 是正方形.
理由如下:
由()知 ,
四边形 是菱形,
,,
,
,
四边形 是正方形.
一、选择题(共8小题)
1. 矩形具有而平行四边形不一定具有的性质是
A. 对边相等 B. 对角相等
C. 对角线相等 D. 对角线互相平分
2. 下列结论中,矩形具有而菱形不一定具有的性质是
A. 内角和为 B. 对角线互相平分
C. 对角线相等 D. 对角线互相垂直
3. 菱形 在平面直角坐标系中的位置如图所示,点 的坐标是 ,点 的纵坐标是 ,则点 的坐标是
A. B. C. D.
4. 正方形具有而菱形不具有的性质是
A. 对角线平分一组对角 B. 对角互补
C. 四边相等 D. 对边平行
5. 如图,在平行四边形 中,, 是 上两点,,连接 ,,,,添加一个条件,使四边形 是矩形,这个条件可以是
A. B.
C. D.
6. 下列说法正确的是
A. 对角线互相垂直的平行四边形是正方形
B. 四角相等的四边形是正方形
C. 四边相等的四边形是正方形
D. 对角线互相垂直平分且相等的四边形是正方形
7. 如图,在 中,, 于点 , 和 的平分线相交于点 , 为边 的中点,,则
A. B. C. D.
8. 如图,在平行四边形 中,, 分别是 和 的平分线.添加一个条件,仍无法判断四边形 为菱形的是
A. B.
C. D. 是 的平分线
二、填空题(共4小题)
9. 如图,在菱形 中,对角线 , 交于点 ,过点 作 于点 ,已知 ,,则 .
10. 如图所示,在四边形 中,,对角线 与 相交于点 .若不增加任何字母与辅助线,要使得四边形 是正方形,则还需增加的一个条件是 .
11. 如图,在矩形 中,对角线 与 相交于点 ,过点 作 ,垂足为点 ,若 ,则 度.
12. 如图,四边形 是正方形, 为等边三角形,, 相交于点 ,连接 ,则 .
三、解答题(共6小题)
13. 如图,在平行四边形 中,点 , 是直线 上的两点,.
(1)求证:四边形 是平行四边形.
(2)若 ,,,四边形 是矩形,求 的长.
14. 如图,在四边形 中,, 是 的中点, 平分 交 于点 .
(1)求证:;
(2)猜想 与 具有怎样的位置关系,并证明你的猜想.
15. 如图,四边形 为正方形,,点 是边 上一动点,在点 移动的过程中,始终保证 ,交 于点 ,求证:.
16. 如图,在 中, 是 边上的一点, 是 的中点,过 点作 的平行线交 的延长线于 ,且 ,连接 .
(1)求证: 是 的中点;
(2)如果 ,试判断四边形 的形状,并证明你的结论.
17. 如图,在 中,,点 是 的中点,, 的平分线 交 于点 ,作 ,连接 并延长交 于点 ,连接 .求证:四边形 是菱形.
18. 已知:如图,在菱形 中,点 ,, 分别为 ,, 的中点,连接 ,,,.
(1)求证:;
(2)当 与 满足什么关系时,四边形 是正方形 请说明理由.
答案
1. C
【解析】矩形的对角线相等,而平行四边形的对角线不一定相等.
2. C
【解析】矩形和菱形的内角和都为 ,矩形的对角线互相平分且相等,菱形的对角线垂直且平分,
矩形具有而菱形不具有的性质为对角线相等.
3. B
【解析】连接 交 于点 ,
四边形 是菱形,
,,,
点 的坐标是 .
4. B
5. A
【解析】因为四边形 是平行四边形,
所以 ,.
因为 ,
所以 ,即 ,
所以四边形 是平行四边形.
若 ,则 ,
所以四边形 是矩形;
若 ,则不能证明四边形 是矩形;
若 ,则四边形 是菱形;
若 ,则不能证明四边形 是矩形.
6. D
【解析】对角线互相垂直的平行四边形是菱形;
四角相等的四边形是矩形;
四边相等的四边形是菱形;
对角线互相垂直平分且相等的四边形是正方形.
7. C
【解析】连接 ,
, 为边 的中点,
,
又 ,
,
是等边三角形,
,
,
,
和 的平分线相交于点 ,
,
,
,故选C.
8. C
【解析】 四边形 是平行四边形,
,,,.
, 分别是 和 的平分线,
,,
.
在 和 中,
.
,又 ,
,又 ,
四边形 是平行四边形.
A项, 四边形 是平行四边形,,
四边形 是菱形,故本选项不符合要求;
B项,,四边形 是平行四边形,
四边形 是菱形,故本选项不符合要求;
C项,根据 和平行四边形 不能推出四边形 是菱形,故本选项符合要求;
D项, 四边形 是平行四边形,
,
.
平分 ,
,
,
,
四边形 是菱形,故本选项不符合要求.
9.
【解析】 四边形 是菱形,
,,,
,
,
,
,
,
又 ,
.
10. 或 、 、 、 四个角中有一个角是直角.
11.
【解析】 四边形 是矩形,
,,.
,
, ,
,
,
,
,
,
,
,
.
12.
【解析】 四边形 是正方形, 是等边三角形,
,,,,,
,,
,
,
,,,
,
,
,
,
.
13. (1) 四边形 是平行四边形,
,.
.
.
又 ,
.
,.
,
四边形 是平行四边形.
(2) ,,,
,
连接 交 于 ,
,
,
四边形 是矩形,
,,,
,
.
14. (1) , 为 的中点,
为 斜边的中线, 为 斜边的中线,
,,
.
(2) 猜想: 垂直平分 .
证明:, 平分 ,
且 ,
即 垂直平分 .
15. 如图,在 上取一点 ,使 ,连接 .
,即 ,
四边形 为正方形,
,
,
.
,
.
,
,
,
,,
,
,
.
16. (1) ,
,
是 的中点,
.
,
.
,
,
,
是 的中点.
(2) 四边形 是矩形.
证明:,,
四边形 是平行四边形,
, 是 的中点,
,
,
四边形 是矩形.
17. ,
,
在 和 中,
,
,
,
四边形 是平行四边形,
,,
,
平分 ,
,
,
四边形 是菱形.
18. (1) 四边形 是菱形,
,,
点 ,, 分别为 ,, 的中点,
,,,,
在 和 中,
.
(2) 当 时,四边形 是正方形.
理由如下:
由()知 ,
四边形 是菱形,
,,
,
,
四边形 是正方形.
同课章节目录
