2022--2023学年人教版八年级数学上册 13.2 画轴对称图形 同步练习 (Word版,含解析)
文档属性
| 名称 | 2022--2023学年人教版八年级数学上册 13.2 画轴对称图形 同步练习 (Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 14:52:38 | ||
图片预览



文档简介
八上(人教版)第十三章 轴对称
13.2 画轴对称图形
一、选择题(共6小题)
1. 如图, 与 关于直线 对称,若 ,,,则 的长度为
A. B. C. D. 以上都不对
2. 现有全等的两个三角形、两个四边形和两个圆,其中一定能组成一个轴对称图形的是
A. 两个三角形 B. 两个四边形 C. 两个圆 D. 以上都不对
3. 点 关于 轴的对称点是
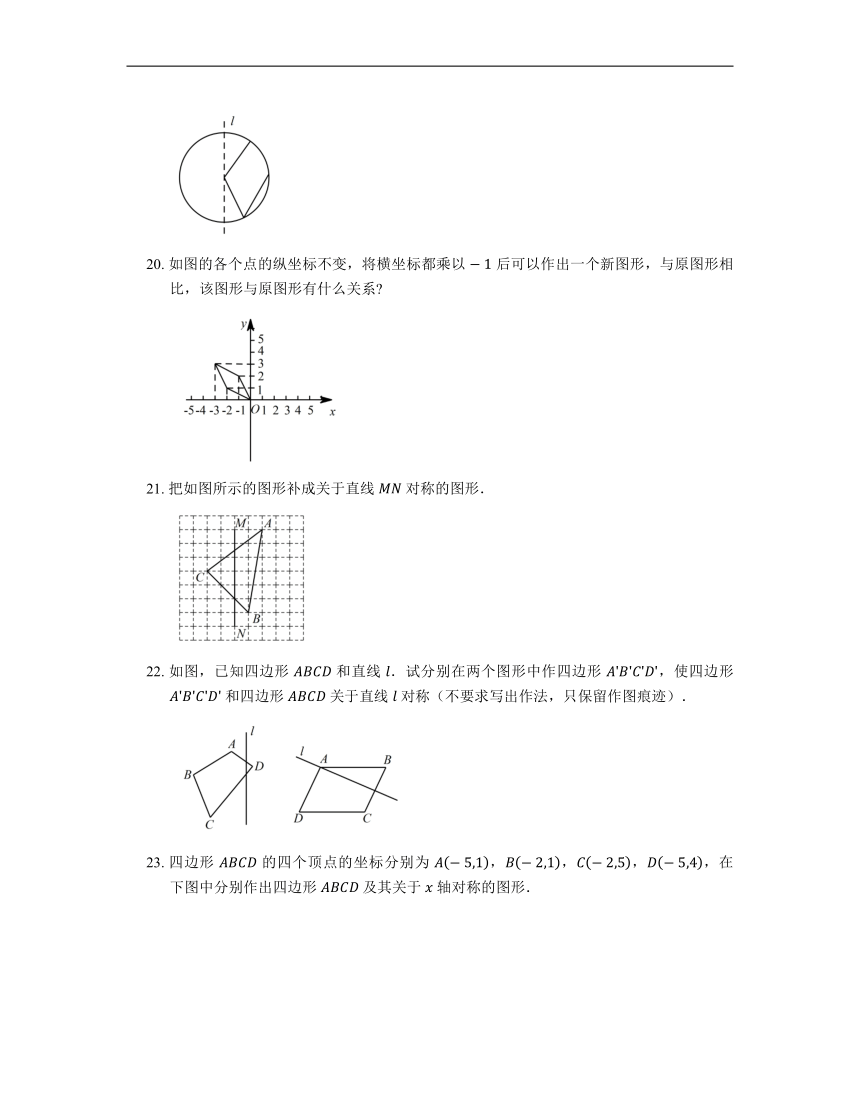
A. B. C. D.
4. 点 与坐标为 的点关于 轴对称.
A. B. C. D.
5. 如果点 的坐标是 ,点 的坐标是 ,那么点 和点 关于 对称.
A. 轴 B. 轴 C. 原点 D. 以上都不对
6. 小明将一块电子手表正对着镜子,发现镜子中的电子手表上显示,则此时电子手表的实际时间是
A. B. C. D.
二、填空题(共11小题)
7. 连接轴对称图形中任意一对对应点的线段都被该图形的对称轴 .
8. 作某个图形关于已知直线的轴对称图形,可以按照以下步骤完成:
()确定该图形中的一些 ;
()作出这些点关于已知直线的 ;
()连接()中所作的点,就得到了所需要的轴对称图形.
9. 点 关于 轴的对称点坐标是 .
10. 点 关于 轴的对称点坐标是 .
11. 将一张坐标纸沿着 轴折叠一次,则与点 重合的点的坐标为 .
12. 若点 和 关于 轴对称,则 , .
13. 点 关于 轴对称的点 的坐标是 ,直线 与 轴的位置关系是 .
14. 如图,已知 和直线 ,作出 关于直线 对称的图形 ,则线段 与直线 的关系为 .
15. 点 与点 关于 轴对称,则 .
16. 已知两点 ,,如果 ,,那么点 和点 关于 对称.
17. 点 关于直线 的对称点 的坐标为 .
三、解答题(共13小题)
18. 如图,已知 和直线 ,请画出以直线 为对称轴的轴对称图形.
19. 如图,这是一个未完成的上海大众汽车的标志图案,该图案是一个以直线 为对称轴的轴对称图形.现已完成对称轴右边部分,请你补全该标志图案.
20. 如图的各个点的纵坐标不变,将横坐标都乘以 后可以作出一个新图形,与原图形相比,该图形与原图形有什么关系
21. 把如图所示的图形补成关于直线 对称的图形.
22. 如图,已知四边形 和直线 .试分别在两个图形中作四边形 ,使四边形 和四边形 关于直线 对称(不要求写出作法,只保留作图痕迹).
23. 四边形 的四个顶点的坐标分别为 ,,,,在下图中分别作出四边形 及其关于 轴对称的图形.
24. 如图,利用关于坐标轴对称的点的特征,作出 关于 轴对称的图形.
25. 已知点 ,,根据以下要求确定 , 的值.
(1), 两点关于 轴对称;
(2), 两点关于 轴对称;
(3) 轴.
26. 已知点 ,点 和点 ,画出 关于直线 对称的图形,并分别写出其对称点的坐标.
27. 已知点 , 关于 轴对称,求 的值.
28. 若 ,点 关于 轴对称的点为 ,点 关于 轴对称的点为 ,试求出点 的坐标.
29. 利用两个全等的三角形可以拼出各种不同的图形.现有规格为 ,, 的两块全等三角板,你能够拼出多少个不同的图形 在下面空白处画出你所能够拼出的图形(要求所拼成的图形是一个轴对称图形,并且两块三角板有重叠部分).
30. 如图,在直角坐标系中,已知直线 是第一、三象限的角平分线.
(1)若点 的坐标为 ,在坐标系中描出点 与点 关于直线 的对称点 ,并写出点 的坐标;
(2)任意写出一个点 的坐标,然后在坐标系中描出该点以及该点关于直线 的对称点 ,并写出点 的坐标;
(3)根据()()中点 与点 、点 与 的坐标特征,你发现关于直线 对称的两个点的坐标有什么规律吗
(4)如果直线 是第二、四象限的角平分线,那么关于直线 对称的两个点的坐标又有什么规律呢
答案
1. C
2. C
3. B
4. A
5. B
6. A
7. 垂直平分
8. ()关键点,()对称点
9.
10.
11.
12. ,
13. ,垂直
14. 垂直平分
15.
16. 轴
17.
18.
即为所求.
19.
20. 如图,新图形与原图形关于 轴对称 .
21.
如图:
即为所求.
22.
23.
24.
25. (1) ,;
(2) ,;
(3) ,.
26. 如图,,,.
27. 点 , 关于 轴对称,
解得:
所以 .
28. 因为 ,
所以 ,,
所以 ,,
所以 .
又因为 与 关于 轴对称,
所以 .
又因为 与 关于 轴对称,
所以 .
29. 以下几种拼法,供参考:
30. (1) 点 的坐标为 ,描点:
(2) 比如点 的坐标为 ,则点 的坐标为 .
(3) 凡是关于直线 对称的两个点的横坐标与纵坐标正好交换位置.
(4) 当直线 是第二、四象限的角平分线时,凡是关于直线 对称的两个点,一个点的横坐标正好与另一个点的纵坐标互为相反数,而这个点的纵坐标又恰好与另一个点的横坐标互为相反数.
13.2 画轴对称图形
一、选择题(共6小题)
1. 如图, 与 关于直线 对称,若 ,,,则 的长度为
A. B. C. D. 以上都不对
2. 现有全等的两个三角形、两个四边形和两个圆,其中一定能组成一个轴对称图形的是
A. 两个三角形 B. 两个四边形 C. 两个圆 D. 以上都不对
3. 点 关于 轴的对称点是
A. B. C. D.
4. 点 与坐标为 的点关于 轴对称.
A. B. C. D.
5. 如果点 的坐标是 ,点 的坐标是 ,那么点 和点 关于 对称.
A. 轴 B. 轴 C. 原点 D. 以上都不对
6. 小明将一块电子手表正对着镜子,发现镜子中的电子手表上显示,则此时电子手表的实际时间是
A. B. C. D.
二、填空题(共11小题)
7. 连接轴对称图形中任意一对对应点的线段都被该图形的对称轴 .
8. 作某个图形关于已知直线的轴对称图形,可以按照以下步骤完成:
()确定该图形中的一些 ;
()作出这些点关于已知直线的 ;
()连接()中所作的点,就得到了所需要的轴对称图形.
9. 点 关于 轴的对称点坐标是 .
10. 点 关于 轴的对称点坐标是 .
11. 将一张坐标纸沿着 轴折叠一次,则与点 重合的点的坐标为 .
12. 若点 和 关于 轴对称,则 , .
13. 点 关于 轴对称的点 的坐标是 ,直线 与 轴的位置关系是 .
14. 如图,已知 和直线 ,作出 关于直线 对称的图形 ,则线段 与直线 的关系为 .
15. 点 与点 关于 轴对称,则 .
16. 已知两点 ,,如果 ,,那么点 和点 关于 对称.
17. 点 关于直线 的对称点 的坐标为 .
三、解答题(共13小题)
18. 如图,已知 和直线 ,请画出以直线 为对称轴的轴对称图形.
19. 如图,这是一个未完成的上海大众汽车的标志图案,该图案是一个以直线 为对称轴的轴对称图形.现已完成对称轴右边部分,请你补全该标志图案.
20. 如图的各个点的纵坐标不变,将横坐标都乘以 后可以作出一个新图形,与原图形相比,该图形与原图形有什么关系
21. 把如图所示的图形补成关于直线 对称的图形.
22. 如图,已知四边形 和直线 .试分别在两个图形中作四边形 ,使四边形 和四边形 关于直线 对称(不要求写出作法,只保留作图痕迹).
23. 四边形 的四个顶点的坐标分别为 ,,,,在下图中分别作出四边形 及其关于 轴对称的图形.
24. 如图,利用关于坐标轴对称的点的特征,作出 关于 轴对称的图形.
25. 已知点 ,,根据以下要求确定 , 的值.
(1), 两点关于 轴对称;
(2), 两点关于 轴对称;
(3) 轴.
26. 已知点 ,点 和点 ,画出 关于直线 对称的图形,并分别写出其对称点的坐标.
27. 已知点 , 关于 轴对称,求 的值.
28. 若 ,点 关于 轴对称的点为 ,点 关于 轴对称的点为 ,试求出点 的坐标.
29. 利用两个全等的三角形可以拼出各种不同的图形.现有规格为 ,, 的两块全等三角板,你能够拼出多少个不同的图形 在下面空白处画出你所能够拼出的图形(要求所拼成的图形是一个轴对称图形,并且两块三角板有重叠部分).
30. 如图,在直角坐标系中,已知直线 是第一、三象限的角平分线.
(1)若点 的坐标为 ,在坐标系中描出点 与点 关于直线 的对称点 ,并写出点 的坐标;
(2)任意写出一个点 的坐标,然后在坐标系中描出该点以及该点关于直线 的对称点 ,并写出点 的坐标;
(3)根据()()中点 与点 、点 与 的坐标特征,你发现关于直线 对称的两个点的坐标有什么规律吗
(4)如果直线 是第二、四象限的角平分线,那么关于直线 对称的两个点的坐标又有什么规律呢
答案
1. C
2. C
3. B
4. A
5. B
6. A
7. 垂直平分
8. ()关键点,()对称点
9.
10.
11.
12. ,
13. ,垂直
14. 垂直平分
15.
16. 轴
17.
18.
即为所求.
19.
20. 如图,新图形与原图形关于 轴对称 .
21.
如图:
即为所求.
22.
23.
24.
25. (1) ,;
(2) ,;
(3) ,.
26. 如图,,,.
27. 点 , 关于 轴对称,
解得:
所以 .
28. 因为 ,
所以 ,,
所以 ,,
所以 .
又因为 与 关于 轴对称,
所以 .
又因为 与 关于 轴对称,
所以 .
29. 以下几种拼法,供参考:
30. (1) 点 的坐标为 ,描点:
(2) 比如点 的坐标为 ,则点 的坐标为 .
(3) 凡是关于直线 对称的两个点的横坐标与纵坐标正好交换位置.
(4) 当直线 是第二、四象限的角平分线时,凡是关于直线 对称的两个点,一个点的横坐标正好与另一个点的纵坐标互为相反数,而这个点的纵坐标又恰好与另一个点的横坐标互为相反数.
