5.7三角函数的应用同步练习—2022-2023学年高一上学期数学人教A版(2019)必修第一册(Word含答案)
文档属性
| 名称 | 5.7三角函数的应用同步练习—2022-2023学年高一上学期数学人教A版(2019)必修第一册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 69.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-29 09:10:57 | ||
图片预览



文档简介
三角函数的应用 练习
1.函数y=-2sin的周期、振幅、初相分别是( ).
A.2π,-2, B.4π,-2,
C.2π,2,- D.4π,2,-
2.一种波的波形与函数y=-sin x的图象相同,若其在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是( ).
A.5 B.6 C.7 D.8
3.如图所示,有一广告气球,直径为6 m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角β=1°,当θ很小时,可取sin θ≈θ,试估算气球的高BC的值为( ).
A.70 m B.86 m C.102 m D.118 m
4.国际油价在某一时间内呈现出正弦波动规律:P=Asin+60(A>0,ω>0,P的单位是美元,t的单位是天).现采集到下列信息:最高油价为80美元,当t=150时达到最低油价.则ω的最小值为 .
5.
一个单摆的平面图如图所示,设小球偏离铅锤方向的角为α(单位:rad),并规定当小球在铅锤方向右侧时α为正角,左侧时α为负角.α作为时间t(单位:s)的函数,近似满足关系式α=Asin,其中ω>0.已知小球在初始位置(即t=0)时,α=,且每经过π s小球回到初始位置,那么A= ;α关于t的函数解析式是 .
6.月均温全称为月平均气温,气象学术语,指一个月所有日期的气温的平均气温.某城市一年中12个月的月均温y(单位:℃)与月份x(单位:月)的关系可近似地用函数y=Asin+a(x=1,2,3,…,12)来表示,已知6月份的月均温为29 ℃,12月份的月均温为17 ℃,则10月份的月均温为( ).
A.20 ℃ B.20.5 ℃
C.21 ℃ D.21.5 ℃
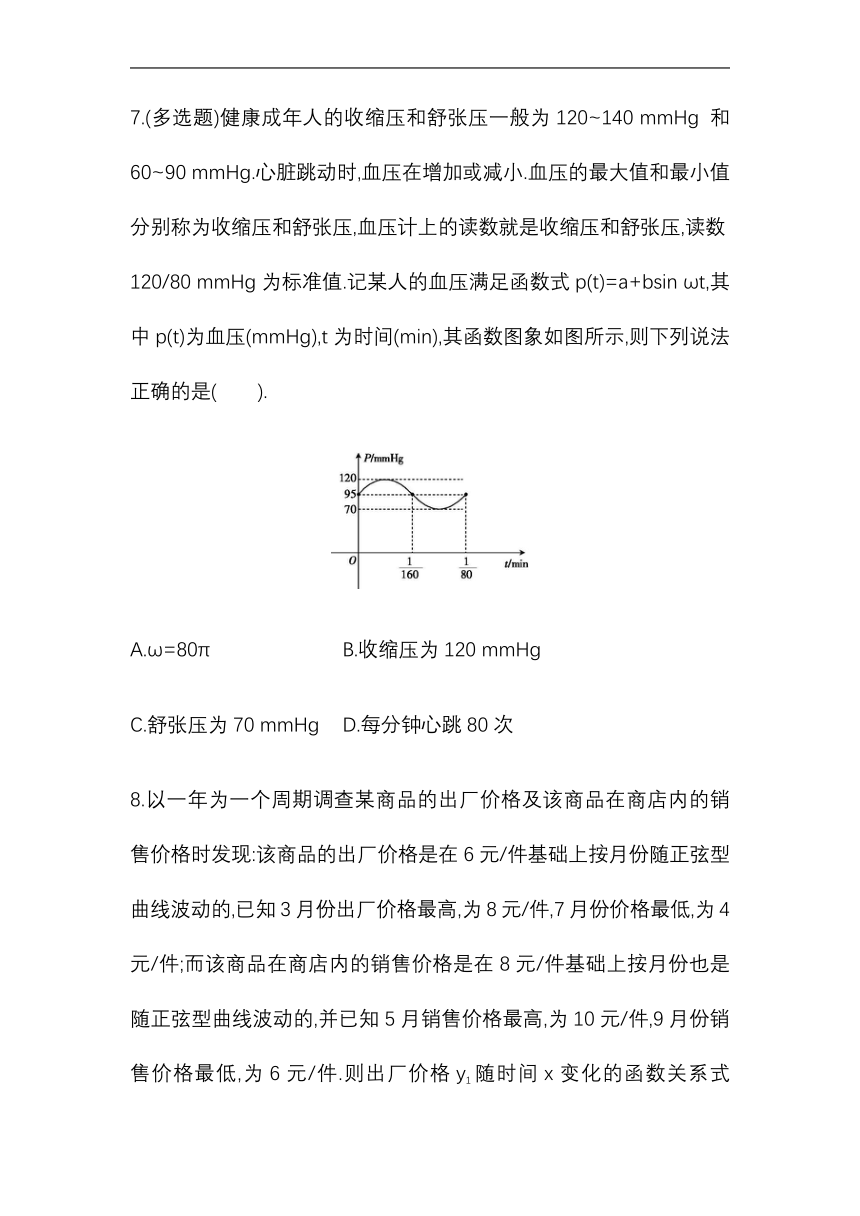
7.(多选题)健康成年人的收缩压和舒张压一般为120~140 mmHg 和60~90 mmHg.心脏跳动时,血压在增加或减小.血压的最大值和最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.记某人的血压满足函数式p(t)=a+bsin ωt,其中p(t)为血压(mmHg),t为时间(min),其函数图象如图所示,则下列说法正确的是( ).
A.ω=80π B.收缩压为120 mmHg
C.舒张压为70 mmHg D.每分钟心跳80次
8.以一年为一个周期调查某商品的出厂价格及该商品在商店内的销售价格时发现:该商品的出厂价格是在6元/件基础上按月份随正弦型曲线波动的,已知3月份出厂价格最高,为8元/件,7月份价格最低,为4元/件;而该商品在商店内的销售价格是在8元/件基础上按月份也是随正弦型曲线波动的,并已知5月销售价格最高,为10元/件,9月份销售价格最低,为6元/件.则出厂价格y1随时间x变化的函数关系式为 ,销售价格y2随时间x变化的函数关系式为 .
9.当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游.下面是一份惠灵顿机场提供的月平均气温统计表.
x(月份) 1 2 3 4 5 6
t(气温:℃) 17.3 17.9 17.3 15.8 13.7 11.6
x(月份) 7 8 9 10 11 12
t(气温:℃) 10.06 9.5 10.06 11.6 13.7 15.8
(1)根据这个统计表提供的数据,为惠灵顿的月平均气温拟合一个函数模型;
(2)当自然气温不低于13.7 ℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
10.长春某日气温y(℃)是时间t(0≤t≤24,单位:时)的函数,下面是某天不同时间的气温预报数据:
t(时) 0 3 6 9 12 15 18 21 24
y(℃) 15.7 14.0 15.7 20.0 24.2 26.0 24.2 20.0 15.7
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成余弦型函数y=Acos(ωt+φ)+b的图象.
(1)根据以上数据,试求y=Acos(ωt+φ)+b(A>0,ω>0,0<φ<π)的表达式;
(2)大数据统计显示,某种特殊商品在室外销售可获3倍于室内销售的利润,但对室外温度要求是气温不能低于23 ℃.根据(1)中所得模型,一个24小时营业的商家想获得最大利润,应在什么时间段(用区间表示)将该种商品放在室外销售 单日室外销售时间最长不能超过多长时间 (忽略商品搬运时间及其他非主要因素)
参考答案
1.D 2.C 3.B
4. 5. α=cos 2t,t∈[0,+∞)
6.A 7.BCD
8.y1=2sin+6 y2=2sin+8
9.【解析】(1)以月份x为横轴,气温t为纵轴作出散点图,并以光滑的曲线顺次连接这些点,得如图所示的曲线.
依散点图所绘制的图象,我们可以考虑用t=Acos(ωx+φ)+k来拟合.
由最高气温为17.9 ℃,最低气温为9.5 ℃,
可得A==4.2,k==13.7.
显然=12,故ω=.
又当x=2时,t取得最大值,所以×2+φ=2kπ,k∈Z,
取φ=-.
所以t=4.2cos+13.7为惠灵顿市常年月平均气温的函数模型.
(2)作直线t=13.7与函数图象交于两点(5,13.7),(11,13.7).这说明每年的十一月初至第二年的四月末,气温不低于13.7 ℃,是惠灵顿市的最佳旅游时间.
10.【解析】(1)根据以上数据知,解得
由=15-3=12,得T=24,所以ω==.
当x=3时,y=14,即6cos+20=14,
解得cos=-1,即+φ=π+2kπ,k∈Z.
所以φ=+2kπ,k∈Z,
由0<φ<π,得φ=,
所以y=6cos+20,t∈[0,24].
(2)令y=6cos+20≥23,
得cos≥,
即-+2kπ≤t+≤+2kπ,k∈Z,
解得-13+24k≤t≤-5+24k,k∈Z,
当k=1时,11≤t≤19,
所以一个24小时营业的商家想获得最大利润,应在t∈[11,19]时间段将该种商品放在室外销售,且单日室外销售时间最长不能超过19-11=8小时.
1.函数y=-2sin的周期、振幅、初相分别是( ).
A.2π,-2, B.4π,-2,
C.2π,2,- D.4π,2,-
2.一种波的波形与函数y=-sin x的图象相同,若其在区间[0,t]上至少有2个波峰(图象的最高点),则正整数t的最小值是( ).
A.5 B.6 C.7 D.8
3.如图所示,有一广告气球,直径为6 m,放在公司大楼上空,当行人仰望气球中心的仰角∠BAC=30°时,测得气球的视角β=1°,当θ很小时,可取sin θ≈θ,试估算气球的高BC的值为( ).
A.70 m B.86 m C.102 m D.118 m
4.国际油价在某一时间内呈现出正弦波动规律:P=Asin+60(A>0,ω>0,P的单位是美元,t的单位是天).现采集到下列信息:最高油价为80美元,当t=150时达到最低油价.则ω的最小值为 .
5.
一个单摆的平面图如图所示,设小球偏离铅锤方向的角为α(单位:rad),并规定当小球在铅锤方向右侧时α为正角,左侧时α为负角.α作为时间t(单位:s)的函数,近似满足关系式α=Asin,其中ω>0.已知小球在初始位置(即t=0)时,α=,且每经过π s小球回到初始位置,那么A= ;α关于t的函数解析式是 .
6.月均温全称为月平均气温,气象学术语,指一个月所有日期的气温的平均气温.某城市一年中12个月的月均温y(单位:℃)与月份x(单位:月)的关系可近似地用函数y=Asin+a(x=1,2,3,…,12)来表示,已知6月份的月均温为29 ℃,12月份的月均温为17 ℃,则10月份的月均温为( ).
A.20 ℃ B.20.5 ℃
C.21 ℃ D.21.5 ℃
7.(多选题)健康成年人的收缩压和舒张压一般为120~140 mmHg 和60~90 mmHg.心脏跳动时,血压在增加或减小.血压的最大值和最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.记某人的血压满足函数式p(t)=a+bsin ωt,其中p(t)为血压(mmHg),t为时间(min),其函数图象如图所示,则下列说法正确的是( ).
A.ω=80π B.收缩压为120 mmHg
C.舒张压为70 mmHg D.每分钟心跳80次
8.以一年为一个周期调查某商品的出厂价格及该商品在商店内的销售价格时发现:该商品的出厂价格是在6元/件基础上按月份随正弦型曲线波动的,已知3月份出厂价格最高,为8元/件,7月份价格最低,为4元/件;而该商品在商店内的销售价格是在8元/件基础上按月份也是随正弦型曲线波动的,并已知5月销售价格最高,为10元/件,9月份销售价格最低,为6元/件.则出厂价格y1随时间x变化的函数关系式为 ,销售价格y2随时间x变化的函数关系式为 .
9.当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游.下面是一份惠灵顿机场提供的月平均气温统计表.
x(月份) 1 2 3 4 5 6
t(气温:℃) 17.3 17.9 17.3 15.8 13.7 11.6
x(月份) 7 8 9 10 11 12
t(气温:℃) 10.06 9.5 10.06 11.6 13.7 15.8
(1)根据这个统计表提供的数据,为惠灵顿的月平均气温拟合一个函数模型;
(2)当自然气温不低于13.7 ℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
10.长春某日气温y(℃)是时间t(0≤t≤24,单位:时)的函数,下面是某天不同时间的气温预报数据:
t(时) 0 3 6 9 12 15 18 21 24
y(℃) 15.7 14.0 15.7 20.0 24.2 26.0 24.2 20.0 15.7
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成余弦型函数y=Acos(ωt+φ)+b的图象.
(1)根据以上数据,试求y=Acos(ωt+φ)+b(A>0,ω>0,0<φ<π)的表达式;
(2)大数据统计显示,某种特殊商品在室外销售可获3倍于室内销售的利润,但对室外温度要求是气温不能低于23 ℃.根据(1)中所得模型,一个24小时营业的商家想获得最大利润,应在什么时间段(用区间表示)将该种商品放在室外销售 单日室外销售时间最长不能超过多长时间 (忽略商品搬运时间及其他非主要因素)
参考答案
1.D 2.C 3.B
4. 5. α=cos 2t,t∈[0,+∞)
6.A 7.BCD
8.y1=2sin+6 y2=2sin+8
9.【解析】(1)以月份x为横轴,气温t为纵轴作出散点图,并以光滑的曲线顺次连接这些点,得如图所示的曲线.
依散点图所绘制的图象,我们可以考虑用t=Acos(ωx+φ)+k来拟合.
由最高气温为17.9 ℃,最低气温为9.5 ℃,
可得A==4.2,k==13.7.
显然=12,故ω=.
又当x=2时,t取得最大值,所以×2+φ=2kπ,k∈Z,
取φ=-.
所以t=4.2cos+13.7为惠灵顿市常年月平均气温的函数模型.
(2)作直线t=13.7与函数图象交于两点(5,13.7),(11,13.7).这说明每年的十一月初至第二年的四月末,气温不低于13.7 ℃,是惠灵顿市的最佳旅游时间.
10.【解析】(1)根据以上数据知,解得
由=15-3=12,得T=24,所以ω==.
当x=3时,y=14,即6cos+20=14,
解得cos=-1,即+φ=π+2kπ,k∈Z.
所以φ=+2kπ,k∈Z,
由0<φ<π,得φ=,
所以y=6cos+20,t∈[0,24].
(2)令y=6cos+20≥23,
得cos≥,
即-+2kπ≤t+≤+2kπ,k∈Z,
解得-13+24k≤t≤-5+24k,k∈Z,
当k=1时,11≤t≤19,
所以一个24小时营业的商家想获得最大利润,应在t∈[11,19]时间段将该种商品放在室外销售,且单日室外销售时间最长不能超过19-11=8小时.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
